
Understanding how to perform calculations involving large or small numbers can greatly enhance your problem-solving skills in mathematics. By mastering these techniques, you can tackle a variety of mathematical challenges more efficiently, especially when working with values that span many orders of magnitude.
In this section, we will explore the methods for manipulating numbers in a compact format, focusing on simplifying and solving complex expressions. You will learn to handle basic operations such as addition, subtraction, multiplication, and division, all while working with numbers expressed in an abbreviated form.
Through clear explanations and practical examples, you will gain a solid foundation in managing these types of problems. We will walk you through each calculation step by step, ensuring that you develop the confidence to approach similar tasks in the future.
Understanding Exponential Calculations
When dealing with very large or very small values, traditional methods of writing numbers become cumbersome. A more efficient way to represent such values is through a compact system that uses powers of 10. This approach simplifies complex calculations and makes it easier to manage numbers across a wide range of scales. In this section, we will break down the fundamental concepts behind manipulating these values and performing arithmetic operations on them.
Key Principles of Exponential Arithmetic
To perform calculations using powers of 10, it’s crucial to understand how the exponents interact. The main operations include adjusting the exponents when adding or subtracting, as well as multiplying and dividing the base numbers while handling the powers. By following a few simple rules, you can solve even the most complicated problems with ease.
| Operation | Rule |
|---|---|
| Multiplication | Multiply the base numbers, then add the exponents. |
| Division | Divide the base numbers, then subtract the exponents. |
| Addition/Subtraction | Align the exponents first, then perform the operation on the base numbers. |
Practical Examples
By applying the rules outlined above, you can solve complex expressions involving powers of 10. For instance, when multiplying two values expressed as powers of 10, you would multiply the base values and add the exponents. Similarly, division involves subtracting the exponents. These simple steps allow you to efficiently handle otherwise unwieldy numbers in calculations.
How to Simplify Exponential Values
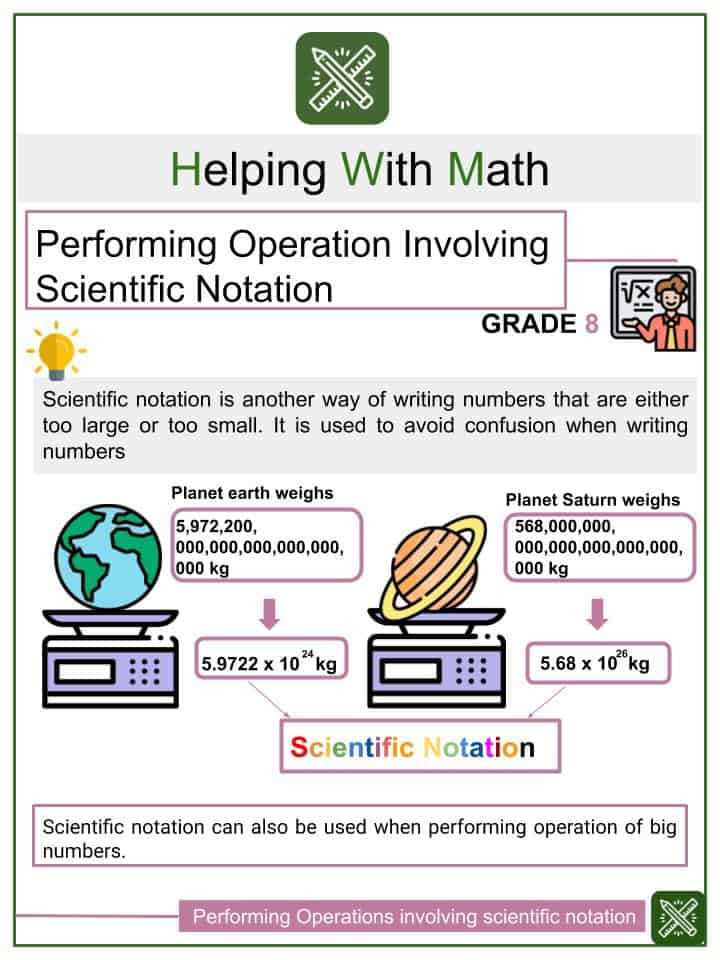
Reducing complex expressions involving large or small numbers into a simpler format is a crucial skill in mathematics. The goal is to represent the values in a more manageable way, making it easier to perform calculations and compare quantities. This process often involves adjusting the powers of 10 and ensuring that the value is expressed with the correct precision.
Steps to Simplify Expressions
To simplify an expression, first ensure that the number is written in a way that the exponent is correctly placed. This typically involves moving the decimal point so that only one non-zero digit is to the left of the decimal. Adjust the exponent accordingly to reflect this shift. Once this is done, the expression will be in its simplest form, allowing for easier manipulation in further calculations.
Example of Simplification
Consider the number 0.00056. To simplify it, move the decimal point four places to the right, making it 5.6. Since the decimal point was shifted four places, the new exponent becomes -4, resulting in the simplified expression: 5.6 × 10⁻⁴. This process works similarly for both very large and very small values.
Adding and Subtracting Exponential Values
When working with values that are expressed in a compact form using powers of 10, adding or subtracting them requires a careful approach. The key is to make sure that the exponents are consistent, allowing for easy manipulation of the base numbers. By following the right steps, you can efficiently perform these calculations and obtain accurate results.
Steps for Adding Values
To add two values, you must first ensure that both have the same exponent. If the exponents differ, adjust one of the values by shifting its decimal point, and modify the exponent accordingly. After aligning the exponents, simply add the base numbers and keep the common exponent.
- Align the exponents by adjusting the decimal point if necessary.
- Add the base values once the exponents match.
- Keep the common exponent in the final result.
Steps for Subtracting Values
The process for subtraction is similar to addition, but this time you subtract the base numbers after aligning the exponents. Ensure that the values are expressed with the same power of 10 before proceeding with the subtraction operation.
- Align the exponents of both values.
- Subtract the base numbers.
- Maintain the common exponent in the result.
Multiplying Exponential Values
Multiplying values expressed as powers of 10 involves a straightforward process. The key steps are to multiply the base numbers and then combine the exponents. By following these steps, you can simplify complex calculations and manage large or small numbers more easily.
Steps for Multiplication
When multiplying, first multiply the base numbers as you would normally. Then, add the exponents together to determine the new exponent for the result. This method allows you to efficiently handle numbers of varying scales without losing precision.
| Step | Action |
|---|---|
| 1 | Multiply the base values. |
| 2 | Add the exponents. |
| 3 | Write the result with the combined base and exponent. |
Example of Multiplication
Consider the multiplication of 2 × 10³ and 3 × 10². First, multiply the base values: 2 × 3 = 6. Then, add the exponents: 3 + 2 = 5. The final result is 6 × 10⁵.
Dividing Numbers Using Exponential Values
Dividing numbers expressed as powers of 10 requires a clear understanding of how to handle both the base values and the exponents. The process involves dividing the base numbers as usual, and then subtracting the exponents to determine the final result. This method simplifies complex calculations, especially when dealing with very large or very small numbers.
To perform division, begin by dividing the base values. Then, subtract the exponent of the divisor from the exponent of the dividend. The result will provide the quotient in its simplified form, making it easy to manage numbers across various scales.
Converting Between Standard and Exponential Forms
Converting between different ways of expressing numbers is a vital skill, especially when working with extremely large or small values. The goal is to transform numbers into a format that is easier to manage and calculate. This process involves adjusting the decimal point and modifying the exponent to reflect the magnitude of the number accurately.
To convert a number to its exponential form, move the decimal point to create a number between 1 and 10, and adjust the exponent based on how many places the decimal was moved. For the reverse process, the decimal is shifted accordingly to return to the standard form.
| Process | Action |
|---|---|
| From Standard to Exponential | Move the decimal to create a number between 1 and 10, and adjust the exponent based on the number of places moved. |
| From Exponential to Standard | Shift the decimal according to the exponent value and return the number to its original scale. |
Common Mistakes in Exponential Calculations
While working with numbers in exponential form, it’s easy to make mistakes that can lead to incorrect results. These errors typically arise from mismanaging the exponents or failing to properly handle the base values. Understanding these common pitfalls and learning how to avoid them can help ensure more accurate calculations and a better grasp of working with large and small numbers.
Typical Errors in Exponential Calculations
One common mistake is failing to align the exponents when adding or subtracting numbers. Another frequent error occurs during multiplication or division, where the exponents are not correctly added or subtracted. Misplacing the decimal point when converting between forms also leads to incorrect results. Paying attention to these details is essential for performing accurate calculations.
| Mistake | Explanation |
|---|---|
| Incorrect Exponent Handling | Failing to properly add or subtract exponents during multiplication or division. |
| Misaligned Exponents | Not adjusting exponents when adding or subtracting values, leading to errors in the base number. |
| Decimal Point Errors | Improper shifting of the decimal point when converting between standard and exponential forms. |
How to Avoid These Mistakes
To avoid these errors, it’s crucial to follow the proper steps for each type of calculation. Double-checking your work and ensuring that all exponents are aligned can significantly reduce the risk of mistakes. Additionally, practicing conversions between forms will help build a more intuitive understanding of the process.
Why Exponential Form is Important in Math

Using a compact way to represent very large or small numbers is essential in various fields of mathematics. It allows for easier manipulation, comparison, and calculation of numbers that are otherwise unwieldy. By reducing complex values into a simplified format, mathematicians can focus on the relationships between numbers rather than being bogged down by their size or scale.
This method plays a key role in many scientific disciplines, engineering problems, and data analysis, where precision and efficiency are crucial. Whether it’s for calculating distances in space or managing statistical data, understanding this technique provides a practical solution to handling extreme values.
Benefits of Using Exponential Form
- Efficiency in Calculation: Reduces the complexity of working with large or small numbers, making calculations quicker and easier.
- Improved Accuracy: Helps maintain precision in mathematical and scientific work by avoiding rounding errors in very large or small values.
- Enhanced Comparisons: Makes it easier to compare numbers of varying magnitudes by putting them into a uniform structure.
Applications in Real-World Scenarios
- Astronomy: Representing the vast distances between stars and galaxies in a manageable format.
- Physics: Describing the tiny measurements of atomic particles or the immense quantities involved in cosmic phenomena.
- Engineering: Simplifying calculations for large-scale structures, electrical circuits, and more.
Using Exponents in Exponential Form
Exponents are a powerful tool in expressing large or small numbers in a manageable format. By representing a number as a base multiplied by a power of 10, we simplify complex calculations and handle extreme values more efficiently. This technique makes it easier to manipulate numbers, whether you’re multiplying, dividing, or converting between forms.
How Exponents Work
The exponent indicates how many times the base number is multiplied by itself. When dealing with powers of 10, the exponent tells us how many places to move the decimal point to the right or left. Understanding how to adjust the exponent is essential for performing calculations and simplifying expressions.
- Positive Exponents: Move the decimal point to the right, indicating a large number.
- Negative Exponents: Move the decimal point to the left, representing a smaller number.
Examples of Exponent Usage

- 10³: Move the decimal point three places to the right, making the number 1000.
- 10⁻²: Move the decimal point two places to the left, resulting in 0.01.
- 5 × 10²: Multiply 5 by 10² (100), yielding 500.
Real-World Applications of Exponential Form
Exponential form plays a critical role in many real-life scenarios where numbers can reach extreme values, either very large or very small. By simplifying these numbers into a more compact format, this method allows professionals across various fields to conduct calculations more efficiently and accurately. Whether in science, technology, or everyday applications, understanding how to work with powers of 10 is essential for solving complex problems.
Applications in Science and Engineering
- Astronomy: Distances between celestial bodies are often so vast that expressing them in standard form would be impractical. Exponential form simplifies these large measurements, making them easier to work with.
- Physics: Physical constants, such as the speed of light or the mass of subatomic particles, are often represented using exponents to express their magnitude efficiently.
- Engineering: Exponential notation is used in fields like electrical engineering and civil engineering, where measurements like resistance, voltage, and forces are dealt with using very large or very small numbers.
Applications in Everyday Life
- Technology: The storage capacity of digital devices, such as hard drives and memory chips, is often expressed in powers of 10 to indicate the enormous number of bytes.
- Medicine: The size of cells, viruses, and other microscopic structures is frequently measured in nanometers or micrometers, which are represented using exponential notation.
- Finance: Large financial calculations, such as national debts or global market valuations, may be simplified with exponential notation to improve readability and ease of comparison.
Understanding the Solution Format
When working through complex calculations or problems, having a clear and consistent format for presenting solutions is essential. This structure helps ensure that each step is understood and that the result can be easily verified. Whether you’re solving equations, simplifying expressions, or performing conversions, a well-organized format allows for more efficient problem-solving and easier review.
Key Elements of the Solution Format
The solution format typically includes several essential components that guide you through the problem-solving process. These include:
- Initial Problem Setup: This shows the problem as presented, with any necessary variables or constants clearly defined.
- Steps for Solution: A logical progression of steps, showing how each part of the problem is tackled. This may involve simplifying numbers, performing calculations, or applying specific rules.
- Final Result: The simplified or calculated solution, displayed in the appropriate format for the problem at hand.
Why a Standard Format Matters
Using a consistent format helps maintain clarity and precision, especially when dealing with complex problems. It makes it easier to track the process, identify mistakes, and confirm that the final solution is correct. This standardization is especially important in subjects like mathematics and science, where accuracy and clarity are crucial.
Key Rules for Working with Exponential Form
When dealing with numbers expressed as a base multiplied by powers of 10, it’s essential to follow specific rules to ensure accuracy in calculations. These rules help manage the magnitude of the numbers, making it easier to perform arithmetic operations like addition, subtraction, multiplication, and division. By mastering these guidelines, you can handle complex calculations with ease and precision.
Multiplication and Division Rules
When multiplying or dividing numbers expressed in exponential form, it’s crucial to apply the following principles:
- Multiplying Bases: Multiply the base numbers directly while adding or subtracting the exponents, depending on the operation.
- Dividing Bases: Divide the base numbers directly and subtract the exponent of the divisor from the exponent of the dividend.
- Adjusting Exponents: When performing either multiplication or division, ensure that the exponents are consistent and follow the correct rules for addition or subtraction.
Addition and Subtraction Rules
For addition and subtraction, the process is slightly different since the exponents must be the same to combine the numbers:
- Same Exponent: If the exponents are already the same, simply add or subtract the base numbers and keep the exponent unchanged.
- Different Exponent: If the exponents are different, adjust one or both numbers to match the exponents before performing the addition or subtraction. This may involve shifting the decimal point of one of the numbers.
Step-by-Step Guide to Solving Problems
Approaching problems in a structured way can significantly improve the accuracy and efficiency of your work. By following a clear, methodical process, you ensure that every step is accounted for and that mistakes are minimized. The key to solving complex problems lies in breaking them down into smaller, more manageable parts.
Here’s a simple approach to solving problems effectively:
- Understand the Problem: Begin by reading the problem carefully to ensure you fully grasp what is being asked. Identify any variables, constants, and the desired outcome.
- Organize the Information: Arrange the given data in a way that makes sense. This could involve converting numbers into a standard form or identifying common factors.
- Choose the Correct Method: Depending on the problem, decide whether you need to multiply, divide, add, or subtract. This will guide how you handle the numbers and their exponents.
- Perform the Calculation: Follow the chosen method step by step. Ensure that you adhere to the rules for manipulating exponents and adjusting the numbers.
- Double-Check Your Work: After calculating, review each step to verify the solution is correct. If needed, perform the calculation again or use an alternative method to confirm the result.
By following this approach, you can approach problems with confidence and ensure accurate results every time.
Practice Problems with Scientific Notation
To improve your skills in handling large and small numbers, practicing various problems is essential. Working through problems allows you to apply the rules you’ve learned and solidify your understanding. By solving these examples, you can build confidence in your ability to manage complex calculations.
Example 1: Multiplying Numbers
Solve the following multiplication problem:
Problem: (3.2 × 104) × (2.5 × 106)
- Step 1: Multiply the base numbers (3.2 × 2.5).
- Step 2: Add the exponents (4 + 6).
- Step 3: Combine the results to express the final answer.
Example 2: Dividing Numbers
Solve the following division problem:
Problem: (6.4 × 107) ÷ (8 × 103)
- Step 1: Divide the base numbers (6.4 ÷ 8).
- Step 2: Subtract the exponents (7 – 3).
- Step 3: Simplify the expression to find the final result.
These problems will give you practice in applying both multiplication and division rules for working with exponential form. Once you’ve completed these examples, try creating your own problems to challenge yourself further.
Verifying Your Answer with Scientific Notation
After performing calculations involving large or small numbers in exponential form, it’s crucial to verify the accuracy of your result. Verification ensures that no errors were made during the process and helps confirm that the final result is correctly expressed. Here are some effective methods to check your work.
Double-Checking the Exponent
When performing arithmetic involving powers of ten, it’s important to check that the exponents were correctly handled. Incorrectly adding or subtracting exponents can lead to significant errors in the result. Here are the steps to verify:
- Review each step to ensure the exponent was applied properly during multiplication or division.
- For multiplication, add the exponents of the powers of ten.
- For division, subtract the exponents of the powers of ten.
Rewriting the Final Answer
After simplifying the expression, rewrite the result in standard form, ensuring that the base number is between 1 and 10. This step is essential because the answer must follow the correct format for exponential representation:
- Ensure the decimal point is properly placed so that the base number is between 1 and 10.
- If the number is too large or too small, adjust the exponent accordingly.
- Double-check the value of the base to ensure it matches the expected result.
By taking these verification steps, you can be confident that your final result is correct and properly formatted. If there are any discrepancies, retracing your steps and adjusting the exponents or base will usually resolve the issue.
Tips for Mastering Scientific Notation Operations
Mastering calculations involving large and small numbers expressed in exponential form requires practice and attention to detail. By understanding the key rules and employing effective strategies, you can approach these problems with confidence and precision. Here are some helpful tips to guide you through the process and ensure accuracy in your results.
1. Practice Regularly
The more you practice working with exponential expressions, the more comfortable you’ll become. Repeated exposure to different types of problems will help solidify the concepts and rules, making it easier to recognize patterns and solve complex calculations. Make sure to work on a variety of problems to strengthen your skills.
2. Understand the Exponent Rules
A strong understanding of how exponents behave during arithmetic operations is crucial. Whether you are adding, subtracting, multiplying, or dividing, knowing how to manage the exponents is key. Take the time to review the rules for handling powers of ten:
- When multiplying, add the exponents.
- When dividing, subtract the exponents.
- For any power of a power, multiply the exponents.
3. Break Down Complex Problems
For more complicated problems, break them down into smaller steps. Focus on one part of the calculation at a time–whether it’s handling the base number or simplifying the exponents. By tackling each aspect separately, you can reduce the likelihood of making mistakes and ensure that the final result is correct.
4. Use a Calculator When Necessary
While understanding the rules is essential, don’t hesitate to use a calculator for checking your calculations. Scientific calculators can handle exponents and large numbers efficiently, saving you time and helping verify your work.
5. Double-Check Your Work
After completing a problem, always double-check your results. This includes reviewing the exponents, making sure the base number is properly adjusted, and verifying that the final answer is in the correct form. A quick review can often catch errors that might have been missed during the initial calculation.
By incorporating these strategies into your study routine, you’ll gradually build proficiency and gain a deeper understanding of working with exponential forms. Consistency and attention to detail will lead to mastery over time.