
Preparing for an important assessment requires not only reviewing key concepts but also understanding how to approach various problems efficiently. Whether you’re studying complex equations or analyzing data sets, having the right tools to check your solutions can significantly boost your confidence and performance.
Comprehending the process of solving different problems is essential for mastering the material. By reviewing common types of questions and their solutions, you can gain deeper insight into the structure of the test and apply the appropriate methods for each challenge.
In this section, we focus on helping you identify the most effective strategies for solving problems and understanding the rationale behind the solutions. By familiarizing yourself with typical question formats and practicing with similar exercises, you can ensure you’re ready to face any challenges that may arise during your assessment.
Assessment Overview
Understanding the structure of your upcoming assessment is crucial for effective preparation. The goal is to become familiar with the types of problems you will face, so you can approach them with confidence. In this section, we’ll cover the key areas of focus, typical question formats, and provide insight into the overall structure to help you organize your study sessions effectively.
The assessment typically covers a range of topics, each testing specific skills and knowledge. Here’s a breakdown of the primary areas to concentrate on:
- Algebra and problem-solving techniques
- Data analysis and interpretation
- Understanding relationships and functions
- Graphical analysis and interpretation
- Geometric principles and calculations
Each section requires different strategies, from solving equations to interpreting visual data. Focus on practice and understanding the logic behind the problems to strengthen your approach. In addition, mastering time management during the test will ensure you can tackle each section without unnecessary stress.
Essential Tips for Preparation
Proper preparation is essential for performing well on any assessment. Focusing on the right areas and developing effective study habits can help you manage time, understand concepts better, and approach each problem with confidence. The following tips are designed to guide your preparation process and maximize your chances for success.
First, review the most important topics and identify areas where you may need extra practice. Breaking down the material into smaller, manageable chunks makes it easier to absorb and retain information. Organizing study sessions around these key topics ensures you’re addressing all relevant concepts without feeling overwhelmed.
Practice regularly with sample problems that mimic the structure and difficulty level of the actual assessment. This not only strengthens your problem-solving skills but also helps you become more familiar with the format, reducing anxiety during the test. Focus on solving problems quickly and accurately to improve your time management.
Lastly, take care of your well-being. Getting enough rest, eating properly, and staying hydrated can have a significant impact on your performance. A clear mind will help you stay focused, solve problems efficiently, and maintain composure throughout the process.
Understanding Key Mathematical Concepts
Grasping the essential principles behind the problems you will encounter is critical for success. A strong foundation in fundamental ideas not only improves your problem-solving abilities but also helps you apply the right techniques to a variety of challenges. In this section, we will explore the core concepts that you need to understand thoroughly before tackling any questions.
Important Topics to Master
The following areas are essential for understanding the framework of the material:
- Algebraic manipulation and equation solving
- Understanding functions and their properties
- Working with statistical data and analysis
- Geometry and spatial reasoning
- Graphical interpretation and analysis
Application of Concepts
Once the core concepts are understood, the next step is to practice their application in various contexts. This involves:
- Recognizing patterns and relationships in problems
- Translating real-world scenarios into mathematical models
- Using formulas to simplify and solve complex problems
- Interpreting data and making logical conclusions
Focusing on these areas will ensure that you can approach any problem with a clear understanding of the underlying principles, leading to more efficient problem solving and better results.
Common Problem Types on the Assessment
Each assessment is designed to test your understanding of various concepts and your ability to apply them in different contexts. Recognizing the common problem types that you may encounter can help you prepare more effectively. Understanding these categories allows you to focus your practice on the areas that are most likely to appear, ensuring a more efficient study process.
Types of Problems

Some of the most common problem categories you may encounter include:
- Solving equations and inequalities
- Graphing functions and interpreting curves
- Data analysis and interpretation
- Understanding geometric shapes and their properties
- Working with word problems involving real-life situations
Problem-Solving Strategies
Each of these problem types requires a specific approach:
- For equations, focus on isolating variables and simplifying expressions
- When working with graphs, ensure you understand how to plot points and analyze trends
- In data problems, identify key patterns and use statistical tools to summarize information
- For geometry, always recall essential formulas and focus on relationships between shapes
- In word problems, break down the situation into smaller parts and translate it into mathematical terms
By familiarizing yourself with these common problem types, you can approach the assessment with greater confidence and accuracy. Practice in each area will prepare you for a variety of challenges, helping you to tackle any question that comes your way.
Time Management During the Test
Efficient use of time is a crucial factor in performing well during any assessment. Without proper planning, it’s easy to become overwhelmed by the number of questions or lose focus. Developing a strategy for managing your time will help ensure you have enough time to address every problem and review your work before the end.
One of the best approaches is to divide your time based on the number of questions and their complexity. Prioritize simpler problems to quickly build momentum, and leave more challenging ones for later when you’re fully engaged. Creating a time plan can help you stay on track and reduce stress.
| Section | Time Allocation | Strategy |
|---|---|---|
| Easy Problems | 30-40% of time | Complete first to build confidence and save time for harder ones |
| Moderate Problems | 40-50% of time | Approach with clear focus, avoid rushing |
| Challenging Problems | 20-30% of time | Leave for last, but allocate enough time to think critically |
By structuring your time efficiently, you will minimize the chances of running out of time and allow yourself to address all problems systematically. Additionally, always leave a few minutes at the end to review your work, as small errors can often be caught with a fresh perspective.
How to Approach Word Problems
Word problems can often be the most challenging type of question, as they require not only understanding the underlying concepts but also translating real-world scenarios into mathematical terms. To effectively solve these problems, it’s important to break them down step by step, ensuring that each part of the question is addressed thoroughly.
Steps to Solve Word Problems
Follow these steps to tackle word problems with confidence:
- Read the problem carefully – Understand what is being asked and identify the key information provided.
- Highlight important details – Look for numbers, relationships, and keywords that indicate what operations to use.
- Translate the problem – Convert the written information into mathematical expressions, equations, or diagrams.
- Identify the solution strategy – Decide which methods or formulas will best help you solve the problem.
- Solve the problem step by step – Follow through with the necessary calculations, ensuring accuracy at each stage.
- Check your work – Review the solution to ensure it makes sense in the context of the problem.
Common Pitfalls to Avoid

- Rushing through the problem without fully understanding the question.
- Missing out on crucial details like units of measurement or relationships between quantities.
- Failing to check the solution against the context of the problem to ensure it’s reasonable.
By taking a systematic approach and avoiding these common mistakes, you can improve your ability to solve word problems effectively and with greater accuracy.
Techniques for Solving Equations
Solving equations requires a methodical approach to isolate the unknown variable and find its value. Whether dealing with linear equations, quadratic expressions, or more complex relationships, mastering various techniques is essential for efficiency and accuracy. In this section, we will explore different strategies that can be applied to a wide range of equations.
One of the most fundamental techniques is simplifying both sides of the equation. This often involves combining like terms, distributing constants, or factoring. The goal is to reduce the equation to its simplest form, making it easier to isolate the variable.
Another useful strategy is the method of balancing, where each operation performed on one side of the equation is mirrored on the other side. This ensures the equality remains intact while gradually isolating the variable.
For more complex equations, such as those involving fractions or exponents, additional techniques such as multiplying both sides by a common denominator or applying logarithms may be required to simplify and solve the equation.
Lastly, always check your solution by substituting the value back into the original equation. This verification step ensures the solution is correct and helps identify any potential mistakes made during the process.
Review of Function and Graphs
Understanding the relationship between variables and how they interact is crucial in many problem-solving scenarios. A function describes this relationship and can be represented graphically. Reviewing key concepts related to functions and their graphs helps in interpreting data, recognizing patterns, and solving various types of problems with greater efficiency.
Functions are mathematical expressions that establish a connection between inputs (independent variables) and outputs (dependent variables). The graph of a function visually displays this relationship, often revealing trends, behaviors, and symmetries that may not be immediately obvious from the equation alone.
When analyzing graphs, pay close attention to key features such as:
- The shape of the graph (e.g., linear, quadratic, exponential)
- The intercepts where the graph crosses the axes
- The slope or rate of change, particularly in linear functions
- Any points of discontinuity or asymptotes in more complex functions
- The domain and range, which specify the possible inputs and outputs of the function
Familiarity with these concepts allows for a deeper understanding of how functions behave and how their graphs reflect important characteristics. Mastery of these principles is essential for solving a wide variety of problems efficiently.
Analyzing Data and Statistics
Data analysis is the process of examining, cleaning, transforming, and interpreting data to uncover meaningful patterns, trends, and insights. Statistics plays a crucial role in this process, providing the tools to summarize and draw conclusions from data sets. Mastering these skills is essential for making informed decisions based on numerical information.
Key Concepts in Data Analysis
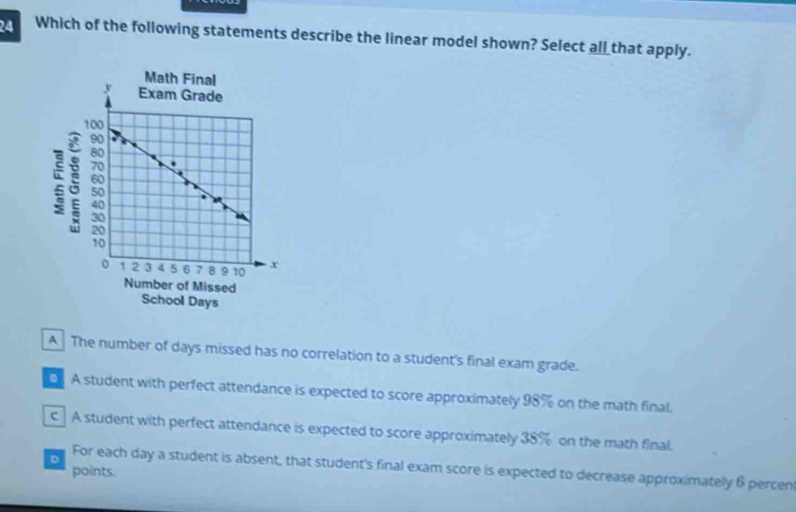
Several important concepts are integral to effective data analysis:
- Measures of central tendency: These include the mean, median, and mode, which provide insights into the average or typical values within a data set.
- Measures of variability: Range, variance, and standard deviation help to understand the spread or dispersion of the data.
- Probability distributions: These describe how values are spread across a given range, helping to predict the likelihood of outcomes.
Interpreting Data in Tables
Tables are commonly used to organize data for easier interpretation. Below is an example of a simple data table showing the test scores of a group of students:
| Student | Score |
|---|---|
| Alice | 88 |
| Bob | 92 |
| Charlie | 85 |
| David | 91 |
| Eve | 89 |
By analyzing this table, one might calculate the average score, determine the most frequent score, and assess the variability in performance. These steps help provide a clearer understanding of the data and guide further decision-making.
Trigonometry Questions on the Exam
Trigonometric questions often involve understanding the relationships between angles and sides of triangles. These problems can range from basic calculations to more complex applications, requiring a solid grasp of key principles. Mastering trigonometric identities, functions, and solving for unknown values is essential for success in this area.
Key Concepts to Remember
Here are the core concepts that frequently appear in trigonometric problems:
- Basic trigonometric ratios: Sine, cosine, and tangent are the fundamental ratios used to relate angles to side lengths in right triangles.
- Unit circle: The unit circle provides a way to define trigonometric functions for all angles, not just those in right triangles.
- Trigonometric identities: Key identities such as Pythagorean, angle sum, and difference formulas are essential tools for simplifying and solving problems.
- Inverse trigonometric functions: These functions allow you to solve for angles when the sides of a triangle are known.
Example of Trigonometric Problem
Consider the following trigonometric problem:
| Problem | Solution |
|---|---|
| Solve for ( theta ) in the triangle where the opposite side is 5 and the adjacent side is 12. | Use the tangent function: ( tan(theta) = frac{opposite}{adjacent} = frac{5}{12} ). Solve for ( theta ) using ( theta = tan^{-1}(frac{5}{12}) ). Result: ( theta approx 22.6^circ ). |
By practicing these types of questions and applying the correct formulas, you can increase your proficiency in solving trigonometric problems and improve your overall performance in this section.
Mastering Algebraic Manipulations
Algebraic manipulation is the process of simplifying, factoring, and rearranging mathematical expressions to solve problems or find unknown values. Being proficient in these techniques is crucial for solving a variety of problems, from simple equations to more complex systems. Mastering these methods enables you to approach and solve a wide range of challenges efficiently.
Essential Algebraic Techniques
Here are some key techniques to focus on when working with algebraic expressions:
- Simplifying expressions: Combine like terms, remove parentheses, and apply distributive properties to make expressions easier to work with.
- Factoring: Factor quadratic expressions or polynomials to solve equations or simplify expressions.
- Solving equations: Isolate the variable by using operations like addition, subtraction, multiplication, and division.
- Substitution: Use substitution to solve systems of equations by replacing variables with equivalent expressions.
Example of Algebraic Manipulation

Consider the equation ( 2x + 3 = 11 ). To solve for ( x ), follow these steps:
- Subtract 3 from both sides: ( 2x = 8 ).
- Divide both sides by 2: ( x = 4 ).
By practicing these techniques and applying them to different types of problems, you will develop a deeper understanding of algebraic concepts and become more efficient at solving equations and simplifying expressions.
Important Geometry Formulas to Know
Geometry involves the study of shapes, sizes, and the properties of space. A solid understanding of the key formulas in this area is essential for solving a wide range of problems. These formulas help you calculate areas, volumes, and other measurements for different types of geometric figures. Knowing them by heart will allow you to quickly and accurately approach geometric problems.
Key Formulas for 2D Shapes
Here are some of the most important formulas for two-dimensional figures:
- Area of a rectangle: ( A = text{length} times text{width} )
- Area of a triangle: ( A = frac{1}{2} times text{base} times text{height} )
- Area of a circle: ( A = pi times r^2 )
- Circumference of a circle: ( C = 2 times pi times r )
- Perimeter of a rectangle: ( P = 2 times (text{length} + text{width}) )
Key Formulas for 3D Shapes
For three-dimensional figures, here are some essential formulas to remember:
- Volume of a cube: ( V = a^3 ), where ( a ) is the side length.
- Volume of a cylinder: ( V = pi times r^2 times h ), where ( r ) is the radius and ( h ) is the height.
- Surface area of a sphere: ( A = 4 times pi times r^2 ), where ( r ) is the radius.
- Volume of a sphere: ( V = frac{4}{3} times pi times r^3 )
Mastering these formulas will give you the foundation to solve geometric problems efficiently. Regular practice will help you apply these equations correctly in different scenarios and improve your problem-solving skills.
Practice Questions for Exam Success
Practicing problems is one of the most effective ways to prepare for any assessment. By solving a variety of questions, you can improve your problem-solving skills and gain confidence in applying the concepts you’ve learned. This section provides a collection of practice questions that will help reinforce key principles and ensure you’re ready for success.
Basic Problem Types
Start with these fundamental problems to build a strong foundation:
- Solve for (x): ( 3x + 5 = 20 )
- Find the area of a triangle: A triangle with a base of 10 units and a height of 6 units.
- Calculate the perimeter: A rectangle with length 12 units and width 8 units.
- Find the volume: A cylinder with a radius of 4 units and height 9 units.
Advanced Problem Types
Once you’re comfortable with basic problems, move on to these more challenging questions:
- Solve the system of equations:
- ( 2x + y = 10 )
- ( x – y = 2 )
- Factor the quadratic: ( x^2 – 5x + 6 = 0 )
- Graph the function: ( f(x) = 2x^2 – 3x + 4 )
- Find the length of the hypotenuse: In a right triangle with legs of length 6 and 8 units.
By working through these problems, you’ll reinforce your understanding of key topics and increase your ability to tackle similar questions with ease during the actual assessment.
How to Interpret Exam Instructions
Understanding the instructions provided during an assessment is crucial for success. Clear interpretation ensures you know exactly what is required for each task and how to allocate your time effectively. Misunderstanding even a small part of the instructions can lead to avoidable mistakes and wasted effort. Here’s how to make sure you’re on track.
Read Thoroughly: Before starting, read all instructions carefully. Pay attention to specific details, such as whether a question asks for a detailed solution or just a final result. Sometimes instructions include important notes about how to format your answers or whether certain assumptions should be made.
Identify Key Action Words: Look for verbs like “calculate,” “simplify,” “explain,” or “compare.” These action words guide how you should approach the task. For example, if a question asks you to “explain,” you may need to provide a justification or reasoning for your answer, rather than just the result.
Pay Attention to Time Constraints: Some assessments may have specific time limits for each section or overall. Understanding these time constraints helps you manage your time wisely. Allocate more time to complex questions, but don’t linger too long on any single task.
Check for Special Conditions: Be aware of any conditions mentioned in the instructions, such as “use only the provided materials” or “round to two decimal places.” These details can influence how you solve a problem and what tools or methods you should use.
Clarify Ambiguities: If you’re unsure about any part of the instructions, take a moment to clarify. If possible, ask the proctor or refer to the guidelines provided. It’s better to seek clarification than to proceed with uncertainty.
By following these steps, you can ensure that you’re interpreting the instructions correctly and can focus on solving the problems effectively and efficiently.
Common Mistakes to Avoid
During any assessment, it’s easy to make simple errors that can impact your performance. Recognizing these common mistakes can help you avoid them and improve your results. Whether it’s misreading instructions, rushing through problems, or forgetting essential steps, awareness is key to success.
1. Misunderstanding the Problem
One of the most common errors is not fully understanding the problem before attempting a solution. This often leads to incorrect assumptions and solutions that don’t match the requirements. To avoid this:
- Take time to read the problem thoroughly.
- Highlight or underline key terms or conditions.
- Rephrase the problem in your own words if necessary.
2. Rushing Through Calculations
When under time pressure, it’s tempting to rush through calculations. However, this often leads to simple arithmetic mistakes or missed steps. To prevent this, try:
- Working carefully and checking each step before moving on.
- Using scratch paper to organize complex calculations.
- Breaking down larger problems into smaller, manageable parts.
3. Skipping Important Details

Small details, like units of measurement or rounding instructions, can easily be overlooked. Skipping these can lead to incorrect or incomplete solutions. To ensure accuracy:
- Read the instructions carefully and check for any specific requirements, such as rounding or format.
- Write out units and convert them if needed.
- Double-check for any constraints or specific conditions mentioned in the problem.
4. Not Reviewing Your Work
Failing to review your answers before submitting can result in overlooked mistakes. A final check can help catch errors that were missed in the initial solution. Tips for a good review include:
- Leaving time at the end of the test to review your answers.
- Rechecking calculations and ensuring all parts of the question have been addressed.
- Looking for logical inconsistencies or discrepancies in your answers.
By avoiding these common mistakes, you can improve your performance and approach each task with more confidence and clarity.
Strategies for Review and Revisions
Effective revision is essential for reinforcing understanding and ensuring preparedness. It involves reviewing key concepts, identifying areas of weakness, and refining skills before tackling more complex tasks. This process requires a balanced approach, focusing on both content and strategy to maximize performance.
1. Prioritize Key Topics
When preparing for an assessment, it’s important to focus on the most relevant topics and areas where you need improvement. To ensure an effective review session, consider:
- Identifying frequently covered concepts or those that carry the most weight.
- Focusing on difficult areas where you feel less confident.
- Creating a list of essential topics that require extra attention.
2. Practice with Sample Problems
Working through sample problems allows you to apply concepts in practical scenarios. This helps you solidify your understanding and boosts your confidence. Strategies for practicing include:
- Using practice tests to simulate real conditions and time constraints.
- Revisiting problems you previously found challenging.
- Analyzing mistakes to understand where and why errors were made.
By consistently applying these strategies, you can sharpen your skills, improve retention, and enhance your overall readiness for the assessment. Remember, revision is not just about memorization, but about understanding and mastering the concepts at hand.
After the Exam: What to Expect
Once the assessment is complete, it’s natural to feel a mix of relief and anticipation. However, the process doesn’t end when you hand in your paper. There are several stages that follow the completion of the test, each with its own set of expectations and steps.
1. Review and Evaluation
After submission, your work will undergo a thorough evaluation. This stage involves assessing how well the material was applied and whether all key aspects were covered correctly. Depending on the assessment format, you can expect:
- Detailed feedback from the examiner or automated scoring systems.
- Insight into areas of strength and those requiring improvement.
- A breakdown of performance in specific sections or types of problems.
2. Receiving Results and Reflection
Once results are made available, it’s time to reflect on your performance. At this point, you will likely receive:
- A grade or score that reflects your overall success.
- A summary of performance, with possible suggestions for further study.
- Opportunity to review the test if there’s a chance for re-assessment or if you wish to clarify any misunderstandings.
In this phase, it’s important to approach the results with an open mind, focusing on both your successes and the areas that could be improved for future assessments. Learning from feedback and analyzing mistakes can provide valuable insights for continued academic or personal development.