
Understanding and mastering the concepts presented in advanced school-level mathematics is a crucial step in a student’s academic journey. This section provides essential support for tackling challenging problems, breaking down complex topics, and ensuring a solid foundation for future learning.
Students often face difficulties when dealing with new material, especially when it involves operations with fractions, decimals, or problem-solving techniques. These lessons build critical thinking and analytical skills, which are key to excelling in higher levels of learning.
By exploring detailed solutions and step-by-step instructions, learners can better grasp difficult subjects and improve their confidence. This resource will help students navigate through challenging tasks, offering clarity and reinforcing the learning process.
Go Math Grade 6 Answer Key Module 6
This section provides a comprehensive guide to solving complex problems encountered in the curriculum for advanced learners. By breaking down each task into manageable steps, students can gain a deeper understanding of the concepts presented and learn effective techniques for finding solutions.
Through detailed explanations and worked examples, this resource helps clarify difficult topics, such as operations with fractions, decimals, and multi-step problems. It is designed to support learners in mastering key skills needed to progress and succeed in their studies.
Whether working through practice exercises or reviewing challenging assignments, this guide offers valuable insights for reinforcing knowledge and boosting confidence. With clear and concise solutions, students can navigate even the most challenging topics with ease.
Overview of Go Math Grade 6
This curriculum is designed to introduce students to a variety of mathematical concepts, focusing on building strong problem-solving and analytical skills. It provides a structured approach to learning, ensuring that students can confidently apply their knowledge to real-world scenarios.
The lessons cover a wide range of topics, from basic arithmetic operations to more advanced concepts such as fractions, decimals, and ratios. Each section is carefully crafted to promote critical thinking, helping learners to understand the logic behind the procedures rather than just memorizing formulas.
By working through progressively challenging exercises, students develop the necessary skills to tackle more complex problems in the future. The curriculum encourages active learning, with ample opportunities for practice and reinforcement to ensure mastery of the material.
Key Topics Covered in Module 6
In this section, students will encounter a variety of essential topics that build a strong foundation for more advanced mathematical concepts. These areas focus on refining skills related to numbers, operations, and problem-solving techniques, which are fundamental for progressing to higher levels of study.
Fractions and Decimals
One of the core areas explored in this unit is the relationship between fractions and decimals. Students will learn how to convert between these two forms, compare values, and apply operations such as addition, subtraction, multiplication, and division.
- Converting fractions to decimals and vice versa
- Comparing and ordering decimals
- Adding and subtracting fractions and decimals
Solving Word Problems
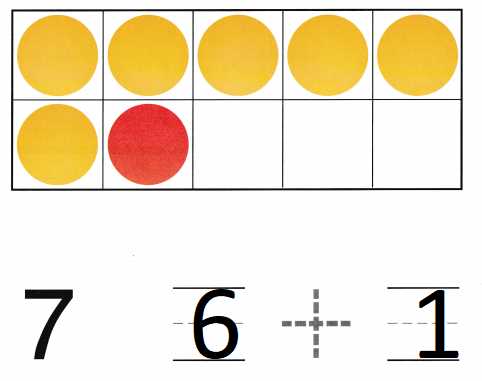
Another important topic is applying mathematical skills to real-world problems. This involves interpreting word problems, extracting relevant information, and using appropriate strategies to find solutions.
- Identifying key information in word problems
- Setting up and solving equations based on problem scenarios
- Using estimation to check the reasonableness of solutions
Understanding Go Math Grade 6 Structure
The structure of this curriculum is designed to provide a clear and progressive learning experience for students. It focuses on building a solid foundation in essential skills, while gradually increasing the complexity of the material to ensure continuous development. The program is organized in a way that allows students to build on previous knowledge and tackle more challenging concepts with confidence.
Each unit is structured to introduce key concepts step-by-step, offering detailed explanations, examples, and practice exercises. The lessons are designed to reinforce understanding through repetition and varied problem-solving techniques, ensuring students gain a deep comprehension of each topic before moving on to the next.
The progression of topics is intentional, starting with basic concepts and advancing toward more complex skills. This ensures that students are not only able to grasp individual topics but also connect them with other areas of learning, creating a cohesive understanding of the subject matter as a whole.
Step-by-Step Solutions for Module 6
This section offers a detailed breakdown of problems presented in the sixth unit, guiding students through each step of the process to reach the correct solution. By following the sequential approach, learners can better understand the logic and reasoning behind each answer, ensuring they grasp the fundamental concepts more effectively.
Solving Fraction Operations
One of the primary focuses in this unit is working with fractions. The following steps outline the process for performing various operations with fractions.
- Step 1: Identify the fractions involved in the problem.
- Step 2: Find a common denominator if necessary.
- Step 3: Perform the operation (addition, subtraction, multiplication, or division).
- Step 4: Simplify the result to its lowest terms.
Understanding Decimal Calculations
Another key area is performing calculations with decimals. The following steps help guide students through the process of handling decimal numbers effectively.
- Step 1: Align the decimal points when adding or subtracting.
- Step 2: For multiplication, multiply as if the numbers are whole numbers, then place the decimal point in the result.
- Step 3: For division, divide as with whole numbers, and adjust the decimal point in the quotient.
- Step 4: Round the result to the desired decimal place if necessary.
How Module 6 Builds Math Skills
This section is designed to strengthen critical problem-solving abilities by progressively challenging students with a variety of tasks. By addressing complex concepts and reinforcing foundational techniques, learners develop a deeper understanding of how to approach and solve mathematical problems effectively.
Through a carefully structured approach, this unit emphasizes hands-on practice, allowing students to actively engage with each concept. As the exercises increase in difficulty, learners refine their skills, boosting both their confidence and competence in dealing with more advanced topics.
The step-by-step problems guide students to explore different methods of solving, enabling them to choose the most effective strategies based on the given problem. This not only enhances their problem-solving flexibility but also fosters a stronger ability to think critically and analytically.
Common Challenges in Module 6
Students often encounter a variety of obstacles when tackling more advanced topics. While these challenges can be difficult, they are also opportunities to develop stronger problem-solving and reasoning abilities. The most common issues stem from the complexity of operations with fractions, decimals, and multi-step word problems.
Fraction Operations
One of the most frequent challenges involves performing operations with fractions. Students may struggle with finding common denominators, simplifying fractions, or correctly applying addition, subtraction, multiplication, and division rules.
| Challenge | Possible Solution |
|---|---|
| Adding/Subtracting Fractions | Ensure common denominators before performing the operation. |
| Multiplying/Dividing Fractions | Multiply numerators and denominators directly, then simplify. |
| Converting Improper Fractions | Convert improper fractions to mixed numbers for easier understanding. |
Word Problems and Multi-Step Solutions
Another common challenge arises when students need to break down word problems into manageable steps. Identifying the key information and applying the correct operations can be overwhelming without a clear strategy.
| Challenge | Possible Solution |
|---|---|
| Extracting Key Information | Highlight important numbers and keywords before starting the problem. |
| Setting Up Equations | Write down the equation based on the problem’s context and operations. |
| Handling Complex Calculations | Break down the problem into smaller, simpler steps to avoid confusion. |
How to Use the Answer Key Effectively
The guide to solutions can be a powerful tool when used correctly. It should not only serve as a way to check results, but also as a resource for understanding the methods and reasoning behind each solution. By approaching the guide thoughtfully, students can use it to reinforce their learning and identify areas for improvement.
Step-by-Step Review
Rather than simply looking at the final result, it’s important to follow the step-by-step process outlined in the solutions. This helps students understand the logic and strategies behind the problem-solving methods, enhancing their skills for similar problems in the future.
| Tip | Explanation |
|---|---|
| Review the Process | Look at each step in the solution to understand how the problem was solved. |
| Analyze Mistakes | If the answer is wrong, compare your approach to the guide’s steps to spot where the mistake occurred. |
| Understand the Methods | Focus on how different strategies are applied to different types of problems. |
Using the Guide for Practice
The solution guide should be used as an additional resource for practice, not as a shortcut. After attempting a problem, compare your solution to the one provided to see if you followed the correct approach. If you didn’t, try again and refer to the guide for clarity.
| Tip | Explanation |
|---|---|
| Self-Check Your Work | After completing a problem, check your solution to make sure it matches the approach in the guide. |
| Identify Patterns | Use the solutions to recognize recurring strategies and techniques for solving similar problems. |
| Strengthen Weak Areas | If certain types of problems are difficult, focus on those areas and practice until you feel more confident. |
Solving Word Problems in Module 6
Word problems often challenge students to apply their understanding of various concepts to real-world scenarios. The key to solving these problems is breaking them down into smaller, manageable steps and identifying the relevant information that will guide the solution process.
To effectively tackle word problems in this unit, students should focus on a few critical steps:
- Read the Problem Carefully: Make sure to understand what is being asked before proceeding.
- Identify Key Information: Look for important numbers, units, and relationships mentioned in the problem.
- Determine the Operations Needed: Decide whether addition, subtraction, multiplication, or division is required based on the context.
- Set Up the Equation: Translate the words into an equation or expression that reflects the problem.
- Calculate and Solve: Perform the necessary operations and check that the solution makes sense in the context of the problem.
Following these steps helps students approach word problems with confidence, systematically applying what they know to find the correct solutions. Practicing these techniques can also improve problem-solving skills and increase overall understanding of the concepts being studied.
Understanding Fractions in Module 6
Working with fractions can be a challenge, but it is essential for mastering more advanced concepts. In this section, the focus is on grasping the fundamentals of fractions, including how to manipulate and simplify them effectively. By developing a clear understanding of fractions, students can tackle a wide range of problems with confidence.
Types of Fractions
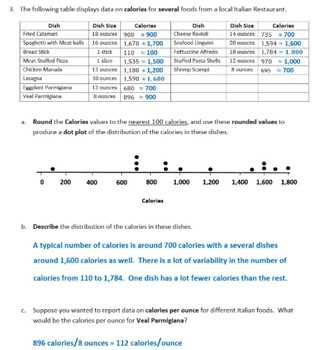
Fractions can be categorized in several ways, depending on how they are used in calculations. Understanding the differences between proper, improper, and mixed fractions is essential for working with them in various contexts.
- Proper Fractions: A fraction where the numerator is smaller than the denominator (e.g., 3/4).
- Improper Fractions: A fraction where the numerator is larger than or equal to the denominator (e.g., 5/3).
- Mixed Numbers: A whole number combined with a fraction (e.g., 1 1/2).
Operations with Fractions
Once students are comfortable with the different types of fractions, the next step is learning how to perform operations like addition, subtraction, multiplication, and division. Each operation requires specific steps, but the key is always to find common denominators when necessary and simplify the results.
- Adding and Subtracting Fractions: Ensure that fractions have the same denominator before performing the operation.
- Multiplying Fractions: Multiply the numerators and denominators directly, then simplify.
- Dividing Fractions: Multiply by the reciprocal of the second fraction.
Mastering these basic concepts of fractions not only provides a strong foundation for more complex problems but also allows for greater flexibility in approaching different types of mathematical challenges. The more practice you get, the more confident you’ll become with using fractions in various scenarios.
Mastering Decimal Operations in Module 6
Working with decimals is a vital skill that students need to develop in order to solve real-world problems accurately. This section covers the essential steps for performing operations such as addition, subtraction, multiplication, and division with decimal numbers. Mastering these operations opens the door to more complex calculations and a deeper understanding of numerical relationships.
Adding and Subtracting Decimals
When adding or subtracting decimal numbers, the key is to align the decimal points before performing the operation. This ensures that the digits are in the correct place value position. Here are the steps:
- Align the Decimal Points: Make sure the decimal points are vertically aligned in each number.
- Add or Subtract as Whole Numbers: Perform the operation as if the numbers were whole numbers.
- Place the Decimal: After the operation, place the decimal point in the answer in the same position as the original numbers.
Multiplying and Dividing Decimals
When multiplying or dividing decimals, students need to follow specific rules to ensure accuracy. The process involves working with the numbers as if they were whole numbers, then adjusting for the decimal places at the end.
- Multiplying Decimals: Multiply the numbers as whole numbers, then count the total number of decimal places in the factors. Place the decimal in the product accordingly.
- Dividing Decimals: If dividing by a decimal, first move the decimal point in the divisor to the right to make it a whole number. Then move the decimal point in the dividend the same number of places. Perform the division as usual and place the decimal in the quotient.
By practicing these steps, students will gain the confidence to handle decimal operations efficiently and accurately, which is crucial for both academic success and real-world problem solving.
Key Strategies for Success in Module 6
To achieve success in this section, it is important to approach the material with the right strategies. By breaking down complex concepts and practicing regularly, students can gain a strong understanding and build confidence in their abilities. Here are some effective strategies that can help improve performance and mastery of the topics covered.
Understanding Concepts Thoroughly
A deep understanding of the fundamental concepts is essential. Instead of memorizing formulas or rules, focus on grasping the underlying principles. When students truly understand why certain steps are taken in solving problems, they are better equipped to tackle any challenges that arise.
- Focus on Understanding: Pay attention to the “why” behind each process, not just the “how”.
- Identify Patterns: Recognize patterns that help simplify problems and make them easier to solve.
- Practice Regularly: Consistent practice helps reinforce understanding and boosts problem-solving skills.
Utilizing Resources Effectively
Using available resources, such as reference materials, practice exercises, and online tutorials, can make a significant difference in mastering the content. Take full advantage of these tools to strengthen skills and clarify any areas of confusion.
- Work Through Examples: Review step-by-step solutions to see the process in action and understand the rationale behind each step.
- Seek Help When Needed: Don’t hesitate to ask for clarification from teachers or peers if certain topics are unclear.
- Use Practice Problems: Practicing different types of problems helps reinforce learning and prepares for various scenarios.
By focusing on these strategies, students can build a solid foundation of knowledge and skills, setting themselves up for success in the upcoming lessons and assessments.
Module 6 Practice Problems Explained
Understanding and solving practice problems is a crucial part of reinforcing what has been learned. By working through a variety of problems, students can apply their knowledge in different contexts and develop a deeper understanding of the concepts. Below, we will break down some common types of practice problems to clarify the steps and logic behind each solution.
Problem 1: Dividing Fractions
One of the key concepts in this section involves dividing fractions. To solve this type of problem, students need to multiply the first fraction by the reciprocal of the second fraction. Let’s take an example:
| Problem | Solution |
|---|---|
| 1/2 ÷ 3/4 | 1/2 × 4/3 = 4/6 = 2/3 |
In this example, the division of 1/2 by 3/4 becomes a multiplication of 1/2 by the reciprocal of 3/4, which is 4/3. After multiplying the fractions, the result is simplified to 2/3.
Problem 2: Decimals and Place Value
Another common challenge is working with decimals, particularly when it comes to understanding place value and rounding. Here’s an example of a typical problem:
| Problem | Solution |
|---|---|
| Round 5.674 to the nearest tenth | 5.674 rounds to 5.7 |
To solve this problem, we look at the digit in the hundredths place (7) to determine whether the tenths place should stay the same or round up. Since 7 is 5 or higher, the tenths place rounds up from 6 to 7, making the rounded number 5.7.
By breaking down each problem step by step, students can not only solve individual problems more effectively but also gain a stronger understanding of how different concepts are interconnected.
Tips for Parents Helping with Module 6

Supporting children in their learning journey can be a rewarding experience, especially when tackling challenging topics. Parents can play a vital role in guiding their children through the various concepts, providing encouragement, and helping them build confidence. Below are some practical tips to assist parents in making the learning process smoother and more effective for their children.
1. Encourage Active Participation
One of the best ways for children to grasp new concepts is by being actively involved in the learning process. Rather than simply giving answers, encourage your child to think through the steps involved in each problem. Asking guiding questions like, “What do you think comes next?” or “Can you explain why you chose that method?” will prompt your child to engage with the material more deeply.
2. Break Down Complex Problems
If your child is struggling with a particular problem, breaking it down into smaller, more manageable steps can help. Focus on one concept at a time, and try not to overwhelm them with too much information all at once. For instance, when dealing with fractions or decimals, tackle each individual operation before combining them. This method ensures that your child builds a solid understanding before moving on to more complex tasks.
By offering gentle support and a clear path forward, parents can help their children succeed in mastering each new concept. Remember to celebrate small victories along the way, as positive reinforcement can boost motivation and foster a love for learning.
Testing Your Understanding of Module 6
Assessing your comprehension of the material covered is crucial to ensure you’re on the right track. Testing your understanding allows you to identify areas where you might need more practice and reinforces the concepts you’ve already grasped. Here are a few strategies you can use to evaluate your knowledge and strengthen your skills.
1. Self-Assessment Through Practice Problems
One of the most effective ways to test your understanding is by solving practice problems on your own. Look back at the exercises and questions you’ve already worked through. Can you complete them without referring to your notes or any resources? If you find yourself struggling, review the steps or concepts involved in solving those problems.
2. Review with a Study Partner
Collaborating with a study partner can help you gain different perspectives on the material. Discuss problems together, explain the steps to each other, and offer suggestions for improvement. Teaching someone else is often a great way to reinforce your own knowledge.
3. Use Online Quizzes and Tests
Online quizzes and practice tests are another excellent way to evaluate your understanding. These resources can provide instant feedback and highlight any areas that need further review. They also help simulate a timed environment, which can be beneficial when preparing for assessments.
4. Reflect on Common Mistakes
Take some time to reflect on the mistakes you made while working through problems. What types of errors did you make–were they due to a misunderstanding of the concept or simply careless mistakes? Understanding where you went wrong is essential for improving your skills and preventing similar mistakes in the future.
- Practice regularly to solidify your understanding.
- Seek help if you’re stuck on a particular concept.
- Focus on mastering key operations before moving to more complex problems.
By testing yourself frequently and reviewing your work, you’ll gain a clearer understanding of the material, helping you to build confidence and succeed in your studies.
Using Go Math for Future Learning
Building a strong foundation early on in education provides a crucial advantage for future learning. The skills developed in the early stages create a framework for tackling more advanced topics later. With the right approach, the concepts learned in this program can serve as a stepping stone toward mastering more complex ideas in the future.
As you progress through various topics, you’ll begin to see how earlier lessons connect with more advanced concepts. This progression encourages critical thinking and problem-solving skills that will be valuable in future academic challenges. By mastering the core concepts now, you’ll be prepared to approach increasingly difficult material with confidence.
One of the key benefits of using this educational program is the development of a systematic approach to solving problems. The focus on step-by-step reasoning will help in subjects that require logical thinking and structured solutions. These skills are essential for succeeding in not just mathematics but also in fields like science, engineering, and even economics.
As you continue to advance in your education, the strategies and techniques you learn today will be applied to a variety of disciplines. For example, understanding how to break down complex problems into manageable steps is a skill that transcends the classroom and becomes an essential tool for real-world situations.
Key takeaways for future learning:
- Logical thinking: The ability to analyze and break down problems will be helpful in every academic discipline.
- Critical reasoning: The techniques used in problem-solving encourage careful thought and consideration of all possible solutions.
- Confidence in tackling new challenges: With each new concept mastered, you gain confidence to approach more advanced subjects with ease.
Ultimately, the knowledge and skills gained here are not only important for immediate success but will also serve as an invaluable tool as you continue your educational journey and prepare for future academic and professional endeavors.
Resources for Extra Practice in Module 6
Supplementary resources are an excellent way to reinforce what you’ve learned and to ensure a deeper understanding of the material. By utilizing additional exercises and practice materials, learners can strengthen their skills and fill in any gaps in their knowledge. There are various tools available to help review concepts, tackle challenging topics, and improve problem-solving techniques.
Here are some helpful resources for extra practice:
- Interactive Websites: Online platforms offer a wide range of interactive exercises, quizzes, and games that help reinforce key concepts. These tools provide immediate feedback, making them valuable for self-assessment and improvement.
- Printable Worksheets: Printable practice sheets allow students to work through problems offline. These resources can often be found in textbooks or online educational platforms, and they allow learners to practice at their own pace.
- Video Tutorials: Instructional videos break down complex concepts into simple, understandable steps. Many educational websites and YouTube channels offer free tutorials tailored to different learning styles.
- Study Apps: Mobile applications can be downloaded for additional practice on-the-go. These apps often feature interactive exercises, flashcards, and quizzes to reinforce knowledge and track progress.
- Peer Study Groups: Collaborating with peers in study groups can be an effective way to tackle difficult problems. Working together allows for different perspectives and problem-solving strategies to be explored.
By taking advantage of these resources, learners can gain a better understanding of the material, increase their confidence, and become more prepared for future challenges. Practice is key to mastery, and with the right tools, success is within reach.