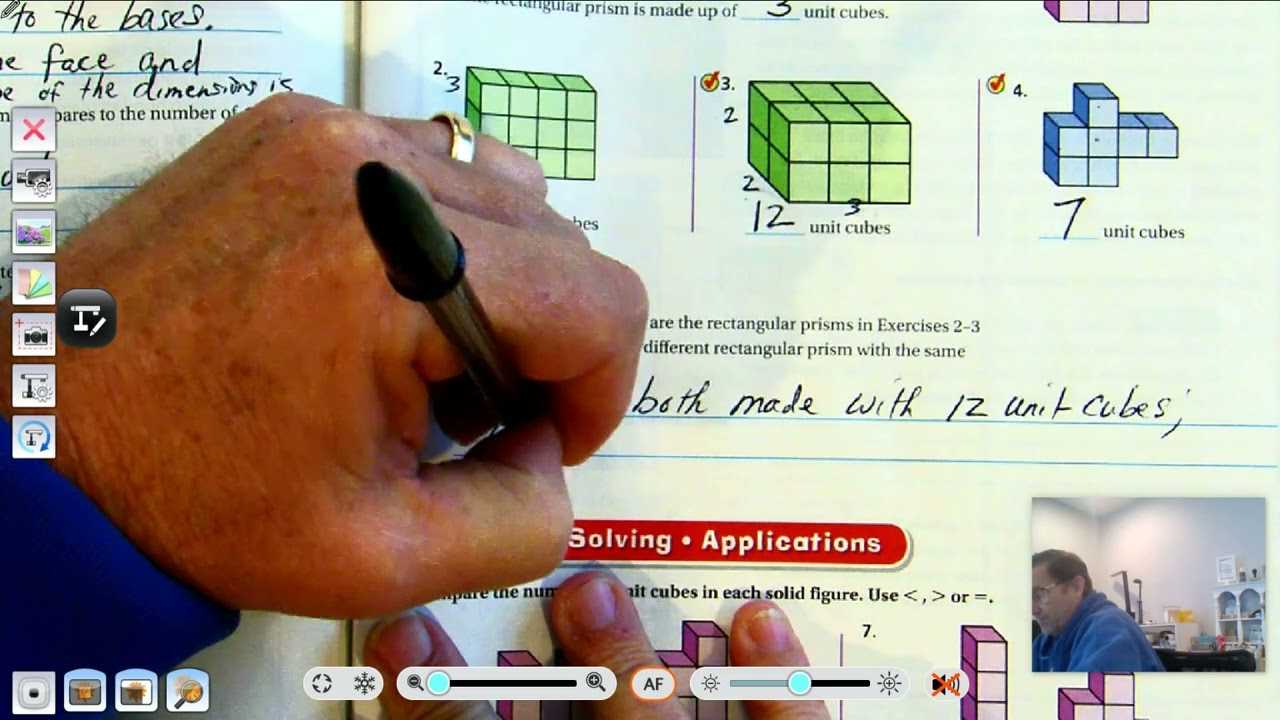
In this section, students are introduced to essential problem-solving techniques that help build a solid foundation for more advanced concepts. Understanding these strategies is crucial for developing confidence and proficiency in mathematical tasks.
The exercises focus on various approaches to tackling complex problems, offering students the opportunity to refine their skills through practice. By mastering these methods, learners can achieve a deeper understanding of the underlying principles and improve their performance.
With detailed explanations and examples, this guide provides a clear path to success. Whether you’re struggling with specific problems or looking to strengthen your overall comprehension, the following sections offer valuable insights to support your progress. Take time to explore each step carefully to ensure you grasp the core concepts effectively.
Go Math Grade 5 Chapter 11 Answer Key
This section provides the solutions to the exercises, breaking down each problem into clear steps. The focus is on offering a comprehensive guide that helps students understand the logic behind every calculation and solution approach. By reviewing these steps, learners can enhance their problem-solving abilities and ensure they grasp the fundamental concepts presented.
Each problem is explained in detail to showcase the necessary operations and reasoning used to reach the correct result. This approach fosters a deeper understanding of the material and prepares students for more complex topics in the future.
| Problem | Solution | Explanation |
|---|---|---|
| Problem 1 | 45 | Apply the distributive property to simplify the equation. |
| Problem 2 | 72 | Use long division to divide the numbers, then check your work. |
| Problem 3 | 58 | Break the numbers into smaller parts and add them sequentially. |
| Problem 4 | 120 | Multiply the values using the commutative property to verify the result. |
| Problem 5 | 96 | Perform subtraction step by step, checking each operation as you go. |
Understanding Chapter 11 Concepts
In this section, we explore the core ideas introduced in the exercises. The primary goal is to equip students with the skills necessary to approach complex problems with confidence. By mastering these concepts, learners can gain a deeper understanding of the subject and develop the ability to apply strategies to a wide range of scenarios.
Key Ideas to Grasp
- Identifying patterns in numbers and operations
- Applying different techniques to solve equations
- Understanding relationships between variables
- Mastering strategies for problem decomposition
How These Concepts Relate to Real-Life Applications
The principles covered in this section go beyond the classroom and have real-world implications. For example, recognizing patterns can be used in budgeting, data analysis, and decision-making. Understanding how to break problems into manageable steps is an essential skill in many professional fields, from engineering to finance.
- Practical applications in daily life
- Connecting abstract ideas with real-world scenarios
- Building problem-solving skills for future challenges
Key Problem Solving Strategies
In this section, we focus on essential approaches that can simplify complex tasks and help students navigate through challenging problems. The goal is to break down problems into smaller, more manageable steps, allowing learners to tackle each part with a clear strategy. By mastering these techniques, students can build confidence and improve their ability to solve a variety of problems efficiently.
Effective Approaches to Problem Decomposition
- Start by understanding the problem fully before attempting to solve it.
- Break down larger problems into smaller, simpler parts to focus on each step.
- Use visual aids like diagrams and charts to represent the problem clearly.
- Identify patterns or similarities with previously solved problems.
Strategies for Verification and Review
- Double-check each calculation to ensure accuracy.
- Review the steps to verify that no part of the problem was overlooked.
- Use reverse operations to confirm the solution.
- Ask questions and seek alternative methods if stuck on a particular step.
Step-by-Step Answer Explanations

This section provides detailed, step-by-step explanations for solving each problem, breaking down the process to ensure clarity. By following these thorough instructions, students can learn how to approach similar tasks with confidence. Each solution is explained in a logical sequence, making it easier to understand the reasoning behind each step and ensuring a comprehensive understanding of the methods used.
By reviewing each step closely, learners can improve their problem-solving skills and reinforce their understanding of the concepts. These explanations not only help with current exercises but also serve as valuable practice for tackling future challenges.
Common Mistakes to Avoid
When tackling problems, it’s easy to fall into certain traps that can lead to incorrect solutions. Understanding these common errors and knowing how to avoid them is crucial for improving accuracy and efficiency. By being aware of these pitfalls, students can develop better problem-solving habits and ensure they are on the right track.
Some of the most frequent mistakes include misinterpreting the question, rushing through steps without double-checking, and neglecting to verify the final result. Taking the time to carefully read each problem and follow the correct procedures can help prevent these errors from occurring.
How to Use the Answer Key
Using a solution guide effectively requires more than just looking up the final result. It’s a tool designed to help you understand the process behind each step and improve your problem-solving techniques. Instead of simply copying the solutions, take the time to review the explanations and break down how each answer was reached.
Start by attempting the problems on your own, and then use the guide to check your work. Focus on comparing your approach to the one provided, noting any differences in the steps taken. This process will help you identify areas for improvement and reinforce your understanding of the concepts involved.
Tips for Successful Learning
To excel in any subject, adopting effective study habits and staying consistent are essential. Success comes not just from understanding the material but from developing the ability to apply it in different contexts. Implementing the right strategies can significantly improve retention and overall performance.
One important tip is to break down complex concepts into smaller, more manageable parts. Tackling smaller sections one at a time helps prevent feeling overwhelmed. Additionally, practice regularly to reinforce what you’ve learned and keep your skills sharp. It’s also crucial to review your work, identify mistakes, and learn from them to ensure continuous improvement.
Practice Problems for Mastery
To truly master any skill, regular practice is essential. This section provides a set of problems designed to help reinforce your understanding and ensure that the concepts are firmly grasped. By working through these problems, you’ll develop the confidence and expertise needed to tackle more complex tasks in the future.
Below are practice problems that will allow you to apply what you’ve learned and test your skills. Work through each problem carefully and take note of any areas where you need improvement.
| Problem | Solution | Explanation |
|---|---|---|
| Problem 1 | 48 | Apply distributive property to break down the multiplication. |
| Problem 2 | 56 | Use long division to divide the numbers accurately. |
| Problem 3 | 120 | Combine like terms and simplify the expression. |
| Problem 4 | 84 | Use subtraction in steps to check for accuracy. |
| Problem 5 | 63 | Apply the commutative property to rearrange and solve. |
Detailed Solution Walkthroughs
This section provides an in-depth breakdown of how to approach and solve specific problems. The goal is to guide you through each step of the process, ensuring that you understand the reasoning behind every decision made. By following these detailed walkthroughs, you’ll gain a deeper understanding of the problem-solving techniques and be able to apply them to new challenges.
Step-by-Step Breakdown
Each solution is broken down into clear, manageable steps. Start by analyzing the problem to identify key information, then move through the necessary operations in a logical order. Be sure to review each step carefully to ensure no part of the problem is overlooked.
Understanding the Process
The walkthrough not only shows you how to arrive at the correct solution but also explains the thought process behind each step. By learning the methods used in these solutions, you’ll be better equipped to solve similar problems on your own in the future.
Key Vocabulary in Chapter 11
Understanding the terminology used in a subject is crucial to mastering the concepts. In this section, we will focus on essential terms that are central to solving the problems and grasping the fundamental ideas covered. By familiarizing yourself with these key words, you’ll enhance your ability to comprehend and apply the material effectively.
Important Terms to Know

- Numerator – The top number in a fraction that indicates how many parts of the whole are being considered.
- Denominator – The bottom number in a fraction that shows how many equal parts the whole is divided into.
- Fraction – A way to express parts of a whole, written as a numerator over a denominator.
- Equivalent – Terms or expressions that represent the same value or amount, though they may look different.
- Decimal – A numerical system based on powers of ten, often used to represent parts of a whole with a decimal point.
Conceptual Understanding
- Common Denominator – A shared multiple of the denominators in two or more fractions, used to simplify operations such as addition or subtraction.
- Mixed Number – A number that combines a whole number and a fraction, such as 3 ½.
- Improper Fraction – A fraction where the numerator is greater than or equal to the denominator.
- Simplify – The process of reducing a fraction to its simplest form, where the numerator and denominator have no common factors other than 1.
Understanding Mathematical Operations
Mathematical operations are the fundamental tools used to manipulate numbers and solve problems. Whether you’re adding, subtracting, multiplying, or dividing, each operation serves a unique purpose and requires a specific approach. Understanding how to use these operations correctly is essential for problem-solving and building stronger reasoning skills.
The Four Basic Operations
- Addition – Combining two or more numbers to find a total or sum.
- Subtraction – Taking one number away from another to find the difference.
- Multiplication – Repeated addition of a number by a specific factor, resulting in a product.
- Division – Splitting a number into equal parts or groups to find how many times one number fits into another.
Advanced Operations and Concepts
- Fractions – Operations involving parts of a whole, including addition, subtraction, multiplication, and division of fractions.
- Order of Operations – The sequence in which operations should be performed to get the correct result, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).
- Exponentiation – Raising a number to the power of another, often used to express repeated multiplication.
- Square Roots – Finding a number that, when multiplied by itself, gives the original number.
Strategies for Effective Studying
Mastering new material requires more than just reading through it quickly. A well-planned study routine and the use of efficient techniques can significantly enhance your understanding and retention. By employing the right strategies, you can approach your learning systematically, making the process more productive and enjoyable.
Effective Study Habits
- Set Specific Goals: Break down the material into smaller, manageable parts and set clear objectives for each study session.
- Active Engagement: Rather than passively reading, actively engage with the content by summarizing, questioning, or teaching it to someone else.
- Regular Review: Consistent review of material strengthens memory retention and helps identify any gaps in understanding.
- Use Study Aids: Flashcards, diagrams, and practice problems are excellent tools for reinforcing concepts and testing your knowledge.
Maximizing Focus and Efficiency
- Create a Quiet Study Space: Minimize distractions by choosing a quiet, organized environment for your study sessions.
- Use the Pomodoro Technique: Study for 25 minutes, followed by a 5-minute break, to maintain focus and prevent burnout.
- Practice Mindfulness: Take a moment to relax and clear your mind before starting to study, which can improve concentration and efficiency.
- Stay Positive and Motivated: Celebrate small successes along the way to stay motivated and keep a positive attitude toward learning.
Utilizing Resources
Making use of available resources, such as study groups, online tutorials, or additional practice materials, can provide further insights and help clarify difficult concepts. Working with peers can also offer new perspectives on problem-solving strategies.
How to Check Your Work

Verifying your results is an essential part of problem-solving. Whether you’re working through complex tasks or simple calculations, checking your work helps ensure accuracy and boosts confidence in your solutions. A systematic approach can catch errors before they become bigger issues, allowing you to correct them efficiently.
Step-by-Step Verification
- Review Your Process: Go over each step you took to solve the problem. Ensure you followed the correct method and didn’t skip any crucial steps.
- Double-Check Calculations: Recheck your numbers and operations. Mistakes often occur with simple arithmetic errors, so take the time to ensure everything adds up correctly.
- Test with Inverse Operations: For many tasks, performing the opposite operation (e.g., division instead of multiplication) can help verify your solution.
- Look for Common Mistakes: Be mindful of frequent errors like misplacing decimal points, mixing up operations, or misinterpreting the question.
Using Alternative Methods
- Check With a Different Approach: If possible, solve the problem in a different way to see if the results match.
- Utilize Tools and Resources: Use calculators, online tools, or reference materials to check your work and ensure consistency.
- Ask for Feedback: Don’t hesitate to seek help from peers or teachers if you’re unsure about your solution or approach.
Printable Answer Sheets for Practice
Having physical copies of problem sets is an excellent way to reinforce your understanding and practice key skills. Printable worksheets allow you to work through tasks at your own pace, providing valuable opportunities for review and improvement. These sheets can be a great addition to your study routine, offering structured practice that can help solidify the concepts you are learning.
Benefits of Printable Worksheets
- Hands-On Practice: Writing out solutions on paper reinforces learning and allows you to engage more actively with the material.
- Portability: With printable sheets, you can practice anywhere, whether at home, in class, or on the go.
- Focused Learning: These worksheets are designed to target specific areas, helping you concentrate on one skill or concept at a time.
- Progress Tracking: You can easily keep track of your progress and identify areas where you need further practice.
How to Use Printable Sheets Effectively
- Start with Easy Exercises: Begin with simpler problems to build confidence before moving on to more complex tasks.
- Use Timed Practice: Challenge yourself by setting a timer to improve speed and efficiency.
- Review Mistakes: After completing a worksheet, go over any errors and make sure you understand why they happened.
- Gradually Increase Difficulty: As you become more comfortable, move on to more difficult worksheets to continue advancing your skills.
Common Questions from Students
As students progress through their studies, it’s natural for questions to arise, especially when learning new concepts. Many learners encounter similar challenges, and addressing these common concerns can help clarify misunderstandings and provide guidance for effective learning. Below are some frequently asked questions that often come up in the learning process.
Frequently Asked Questions
- How can I better understand the material?
To grasp concepts more effectively, try breaking down the material into smaller parts and practicing regularly. Seeking additional resources like videos, practice worksheets, or explanations from peers or teachers can also provide clarity. - What should I do if I make a mistake?
Mistakes are an essential part of learning. After identifying the error, review the steps carefully to understand where the problem occurred. Practicing similar problems will help reduce mistakes in the future. - How do I know if I’m on the right track?
Consistent practice and self-assessment are key. After completing an exercise, check your work against solutions or discuss it with someone knowledgeable. If you arrive at the correct answers or make improvements over time, it’s a good sign you’re progressing. - What should I do if I don’t understand the concept right away?
It’s important to be patient. Revisit the material after a break or try approaching the problem from a different angle. Don’t hesitate to ask for help from a teacher, tutor, or classmate if necessary. - How can I improve my speed and accuracy?
Practice regularly to build both speed and confidence. Setting a time limit for each problem can also help improve efficiency. Start with easier questions and gradually increase the difficulty level to build both speed and accuracy.
How to Improve Math Skills
Improving your abilities in problem-solving and numerical reasoning requires consistent practice and a focused approach. Mastering various mathematical techniques is not just about memorizing formulas, but about understanding the underlying principles and building confidence through repetition. Below are some effective methods for strengthening your mathematical skills.
1. Practice Regularly
The key to enhancing your skills is consistent practice. Set aside time each day to work on problems, starting with basic ones and gradually progressing to more complex exercises. The more you practice, the more you will develop a deeper understanding of the subject.
2. Break Down Complex Problems
When faced with challenging problems, it’s essential to break them down into smaller, more manageable parts. By doing so, you can tackle each step with greater focus and confidence. This method helps reduce overwhelm and makes complex problems easier to solve.
3. Use Visual Aids
Visualizing problems can significantly aid in understanding. Diagrams, graphs, and charts can help clarify abstract concepts, making them easier to comprehend. For example, drawing a number line or creating a table can help you visualize relationships between numbers or quantities.
4. Understand the “Why”
Instead of simply memorizing procedures, focus on understanding why certain methods work. This will help you apply the concepts more flexibly in various situations. Understanding the logic behind each step enhances long-term retention and problem-solving ability.
5. Learn from Mistakes

Making mistakes is an essential part of the learning process. Instead of viewing errors negatively, use them as opportunities to understand what went wrong and how to correct it. Revisiting mistakes and practicing similar problems will improve both accuracy and confidence.
6. Seek Help When Needed
If you encounter difficulties, don’t hesitate to ask for help. Teachers, tutors, or online resources can provide valuable explanations and alternative approaches. Collaborative learning with classmates can also offer new perspectives and enhance your understanding.
Applying Chapter 11 in Real Life
Understanding the concepts presented in this section can have a lasting impact beyond the classroom. The skills developed through solving various numerical problems are applicable in numerous real-world situations. Whether it’s managing personal finances, planning a trip, or making decisions based on measurements, the ability to apply mathematical reasoning is an invaluable tool in everyday life.
1. Budgeting and Money Management
One practical way to apply what you’ve learned is in budgeting and managing personal finances. Whether you are tracking your allowance, saving for something special, or planning a family vacation, understanding how to calculate costs, compare prices, and work with different units of money is crucial. For example, using percentages to calculate discounts or understanding how to divide expenses fairly can help in making sound financial decisions.
2. Cooking and Recipes
Cooking provides an excellent opportunity to apply various mathematical concepts, such as measurements, proportions, and fractions. When following a recipe, you may need to adjust the amounts of ingredients based on the number of servings. For instance, doubling or halving a recipe involves multiplication or division, while accurately measuring ingredients involves understanding units and conversions.
3. Home Improvement Projects
When working on home improvement projects, measuring dimensions, calculating areas, and understanding ratios can help you estimate materials needed and costs involved. Whether you are laying out a garden, installing flooring, or building furniture, these skills will ensure precision and prevent unnecessary waste of resources.
4. Planning Travel and Routes
Whether you’re planning a trip or simply calculating travel time, understanding units of measurement, time calculations, and the concept of ratios is essential. Estimating travel time based on speed and distance, or converting currency for international travel, are practical applications where problem-solving skills come in handy.
Additional Resources for Help
If you’re looking for further support to master the concepts presented, there are a variety of resources available that can provide clarity and additional practice. These tools and platforms can enhance your understanding and provide personalized assistance, making it easier to overcome challenges and reinforce what you’ve learned.
1. Online Learning Platforms
There are numerous websites offering interactive lessons, quizzes, and tutorials designed to help students strengthen their skills. Websites like Khan Academy and IXL offer free exercises and videos that break down complex ideas into easy-to-understand steps. These platforms allow learners to practice at their own pace, with instant feedback to correct mistakes and ensure comprehension.
2. Educational Apps
Mobile applications can be a fun and convenient way to learn. Many apps cater specifically to students, offering personalized practice problems and step-by-step guides. Apps like Photomath allow students to scan problems and receive detailed solutions, helping them understand each step in the process. These apps are a great option for on-the-go practice and quick assistance.
3. Tutoring Services
For students who prefer one-on-one support, professional tutoring services can provide customized help. Tutors are available online or in person and can tailor lessons to fit your unique needs. Whether you’re struggling with specific topics or looking for enrichment, a tutor can offer targeted lessons and strategies to improve your performance.
4. Teacher and Peer Support
Never underestimate the value of asking for help from teachers or classmates. Teachers can offer clarifications and explanations, while peer study groups provide an opportunity to learn together. Explaining concepts to others can also deepen your own understanding, so joining or forming a study group can be a great way to reinforce the material.
5. Workbooks and Practice Sheets
For those who prefer traditional methods, workbooks and printed practice sheets are always helpful. These resources allow you to work through problems on paper and review solutions at your own pace. Many educational publishers offer practice sheets specifically designed to target the skills and concepts covered in various learning sections.