When tackling mathematical challenges, having access to reliable resources can significantly enhance your understanding. This section is dedicated to providing the necessary tools for tackling complex problems with ease and confidence. By exploring structured solutions and step-by-step explanations, learners can deepen their grasp of essential concepts and improve problem-solving abilities.
Unlocking the full potential of practice materials becomes easier when students are guided through each step. With clear solutions, they can not only verify their answers but also understand the logic behind each method. This helps foster critical thinking and equips learners with the skills needed to approach future tasks independently.
By mastering fundamental techniques and refining problem-solving strategies, you can approach each new challenge with greater confidence. This guide serves as a valuable tool for both beginners and advanced learners aiming to improve their skills and achieve academic success in mathematics.
Geometry Nation Answer Key Overview
This section offers an in-depth look at the guide designed to help learners navigate through mathematical exercises. With structured solutions and thorough explanations, it provides the support needed to solve complex problems confidently. The goal is to present the steps and methodologies that make it easier for individuals to understand the process behind each solution, enhancing their problem-solving skills.
The resource is tailored to meet the needs of students at various levels, offering both straightforward solutions and detailed breakdowns of more intricate topics. By offering these insights, the tool helps users not only check their work but also grasp the reasoning behind each answer, enabling them to approach future challenges with a clearer mindset.
Through this guide, students can engage with math problems more effectively, learning how to approach tasks systematically and independently. The overview ensures that learners can make the most of their study sessions, gaining confidence as they refine their mathematical skills.
How to Use the Geometry Nation Key

Learning to effectively utilize a guide for solving mathematical exercises is crucial for mastering the concepts. This section explains how to approach and make the best use of the available resource, ensuring that you not only find the correct solutions but also understand the reasoning behind each step. By following the outlined methods, students can gain confidence in their problem-solving abilities and enhance their overall understanding.
Start by identifying the specific exercise or problem you need help with. Once you’ve located the relevant section in the guide, follow the provided instructions closely. Pay attention to the step-by-step breakdowns, as these will help you comprehend the process behind reaching the correct answer. For complex problems, refer to the additional tips and notes that offer further clarification.
| Step | Action |
|---|---|
| 1 | Find the exercise you’re working on |
| 2 | Follow the structured breakdown for each solution |
| 3 | Refer to additional tips for deeper understanding |
| 4 | Verify your answer and evaluate your approach |
By carefully following this guide, you can ensure that you’re not only getting the right solutions but also developing a deeper understanding of the methods that can be applied to future exercises.
Step-by-Step Solutions for Geometry Nation
This section offers a detailed, structured approach to solving mathematical problems, providing clear, sequential steps that guide you from start to finish. Each solution is broken down into manageable parts, making it easier to understand complex concepts and apply the appropriate methods. By following these steps, students can reinforce their problem-solving skills and improve their understanding of various topics.
The goal is to help you grasp each concept more thoroughly, ensuring that you can confidently tackle similar problems in the future. The solutions are designed to be clear and direct, with explanations that help you understand not just the “how” but also the “why” behind each step.
- Step 1: Identify the problem and review the given information.
- Step 2: Break down the problem into smaller, manageable parts.
- Step 3: Apply the appropriate methods or formulas to solve the problem.
- Step 4: Check your work and ensure that all steps are logically followed.
- Step 5: Review the final solution and verify its accuracy.
By following this systematic approach, you’ll be able to solve problems efficiently and gain a deeper understanding of mathematical concepts. This step-by-step guide ensures that you’re not just memorizing solutions but actually learning the techniques needed to solve future exercises with confidence.
Understanding the Key’s Structure
Grasping the layout and organization of a problem-solving guide is essential for making the most of the resource. The structure is designed to be intuitive, allowing you to quickly locate solutions and follow logical sequences in your approach. Each section is carefully organized to provide clarity, ensuring that users can easily navigate through various exercises and find the necessary explanations.
Each solution is broken down into clear steps, presenting the methods used to solve a particular problem. This structure not only helps in checking your work but also fosters a deeper understanding of the reasoning behind each solution. By following the guide’s layout, you will develop a better grasp of how to approach different types of exercises.
The organization of the guide ensures accessibility, allowing you to jump directly to the sections that are most relevant to your needs. Whether you are looking for a specific type of solution or need assistance with a particular method, the structure provides a logical flow that makes problem-solving more efficient and manageable.
Common Mistakes and How to Avoid Them
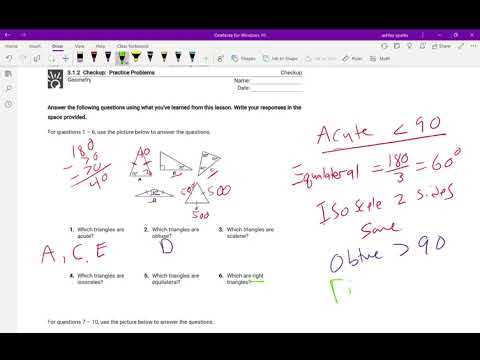
When working through mathematical exercises, it’s easy to overlook certain details or make errors in reasoning that can lead to incorrect solutions. Recognizing and understanding these common mistakes is essential for improving accuracy and efficiency. This section highlights the most frequent pitfalls students encounter and provides tips on how to avoid them in future problem-solving tasks.
A major mistake often occurs when essential information is misinterpreted or ignored. For example, missing key values or failing to apply the correct formula can result in inaccurate answers. Another common error is rushing through the steps without thoroughly checking each one, leading to minor yet significant mistakes in the final solution.
To avoid these pitfalls, it’s important to carefully read the problem, ensure all details are understood, and double-check each step of the process. Taking your time to review the work before finalizing it can prevent these issues and strengthen your ability to solve problems correctly.
Tips for Better Geometry Problem Solving

Improving your problem-solving skills involves more than just practicing exercises; it requires developing a deeper understanding of the concepts and strategies that drive solutions. This section offers practical advice to enhance your ability to solve complex mathematical problems more efficiently and with greater accuracy.
One of the most effective strategies is to break down each problem into smaller, more manageable steps. Rather than tackling everything at once, focus on identifying the key components and how they relate to each other. This approach not only helps reduce mistakes but also makes it easier to spot patterns that can lead to quicker solutions.
Another crucial tip is to stay organized and methodical throughout the entire process. Ensure that each step is clearly written out, with all necessary formulas or methods applied correctly. Avoid skipping steps, even if they seem simple, as this can lead to errors that compound later on.
Finally, take time to review and reflect on your solutions. Checking your work against the original problem can help ensure accuracy, and reviewing mistakes can offer valuable lessons for future exercises. By following these tips, you will strengthen your problem-solving skills and increase your confidence in tackling even the most challenging tasks.
Mastering Geometry Concepts with the Key
Achieving mastery in mathematical principles requires more than just solving problems; it involves understanding the underlying concepts and knowing how to apply them to a wide range of exercises. This section focuses on how to use a structured resource to deepen your comprehension of key principles and enhance your ability to approach complex tasks with confidence.
The first step towards mastery is understanding the logic behind each method and solution. By examining detailed explanations, you can learn not only how to arrive at the correct answer but also why specific techniques are used. This deeper understanding makes it easier to apply the same principles to different types of problems.
As you progress, focus on reinforcing your knowledge by revisiting difficult concepts and reviewing how they were tackled in the guide. Repetition and practice are essential for solidifying understanding and improving your problem-solving speed. Regularly engaging with the material will also help you recognize patterns and shortcuts, allowing for more efficient work in the future.
With continuous effort and a systematic approach, you can gain mastery over even the most challenging topics, enabling you to solve problems with both precision and ease.
Why Geometry Nation Is Effective for Learning
The effectiveness of a learning resource lies in its ability to present information clearly and offer the support necessary to grasp complex concepts. This platform stands out because it not only provides answers but also guides students through each step of the problem-solving process. It’s structured to help learners build a deeper understanding while reinforcing essential skills along the way.
Here are some reasons why this resource is effective for learning:
- Clear Step-by-Step Explanations: The guide breaks down each problem into smaller, digestible parts, helping students understand the logic behind each step.
- Comprehensive Coverage: It covers a wide range of topics, ensuring that learners can find support for various concepts and methods.
- Builds Confidence: By working through problems methodically, students can improve their problem-solving abilities and gain confidence in their skills.
- Self-Paced Learning: The resource allows learners to work at their own pace, reviewing concepts as needed and reinforcing their knowledge without pressure.
By providing structured guidance, reinforcing key concepts, and encouraging independent learning, this platform is an invaluable tool for students aiming to strengthen their skills and deepen their understanding of the subject.
Exploring Key Features of Geometry Nation
This section delves into the distinctive features of the learning platform, highlighting the tools and resources that make it an effective aid for students. These features are designed to enhance understanding, provide clear guidance, and allow for an interactive learning experience. By examining these aspects, students can better utilize the platform to maximize their learning potential.
Comprehensive Problem Solving Guides
One of the standout features is the detailed problem-solving guides that break down complex tasks into manageable steps. These guides help learners understand not just the steps needed to reach a solution, but also the reasoning behind each method. By following the logical progression, students can develop a deeper understanding of the concepts at hand.
Interactive and User-Friendly Layout
The platform’s intuitive layout allows for easy navigation, making it simple for students to locate the resources they need. Whether searching for a specific problem or browsing through various topics, the user-friendly interface ensures that learners can focus on solving problems without unnecessary distractions. This seamless design supports efficient learning and enables students to move quickly through the material.
Practice Exercises Explained

This section focuses on the practical exercises available to students, designed to reinforce core concepts and improve problem-solving skills. Each exercise is carefully crafted to challenge learners while offering a clear path to the correct solution. By engaging with these tasks, students can apply what they’ve learned and solidify their understanding of key principles.
The exercises range in difficulty, allowing students to start with foundational problems and gradually progress to more complex scenarios. Each task is accompanied by step-by-step instructions, ensuring that students not only practice but also understand the reasoning behind each solution. This approach helps bridge the gap between theory and application.
In addition to helping with comprehension, these exercises foster critical thinking skills. By tackling various types of problems, students learn to approach different challenges with confidence and precision, preparing them for even more advanced topics in the future.
Using the Answer Key for Study Sessions

Effective study sessions involve not only reviewing material but also actively engaging with it to deepen understanding. This section explores how to incorporate a solution guide into your study routine, turning it into a valuable tool for reinforcing concepts and improving problem-solving skills.
Here are some strategies for using the solution guide during study sessions:
- Review after Attempting Problems: Before checking the solutions, try solving the problems on your own. Once you’ve made an attempt, use the guide to check your work and identify any mistakes.
- Understand the Process: Instead of just copying the answers, focus on understanding the steps taken to arrive at the solution. This will help you apply the same methods to similar problems.
- Identify Patterns: As you work through different problems, use the solution guide to spot recurring techniques or strategies. Recognizing these patterns will help you approach new problems more confidently.
- Practice Regularly: Incorporate the solution guide into regular practice sessions. This ongoing engagement ensures that you don’t just memorize solutions but also reinforce the underlying concepts.
By using the guide in a thoughtful and systematic way, you can transform study sessions into an opportunity for deeper learning and more effective retention of key concepts.
How to Find Specific Answers Quickly

When studying or solving problems, it’s crucial to be able to locate the correct solutions efficiently. This section discusses strategies to help you quickly find the information you need, minimizing the time spent searching and maximizing the time spent learning and practicing.
Here are some effective ways to find specific solutions fast:
- Use Keywords: Focus on specific keywords related to the problem you’re solving. This allows you to narrow your search and find relevant solutions more quickly.
- Organized Resources: Ensure that the material is organized in a way that allows easy access. If the solutions are grouped by topics or types of problems, it becomes much simpler to locate specific sections.
- Practice Navigation: Familiarize yourself with the structure of the guide or resource. Knowing where to look for certain types of answers will save you valuable time.
- Cross-reference with Examples: If you are looking for a solution to a specific problem type, reviewing similar examples can quickly point you to the exact method or answer.
Example of Efficient Navigation:
| Problem Type | Solution Location |
|---|---|
| Algebraic Equations | Section 1, Pages 5-10 |
| Quadratic Functions | Section 2, Pages 11-15 |
| Linear Graphs | Section 3, Pages 16-20 |
By following these strategies, you can quickly find the right solutions and spend more time focusing on improving your understanding and skills.
Why Practice is Essential
Consistent practice is crucial when mastering any subject, particularly when dealing with complex concepts. It helps reinforce understanding, improves problem-solving skills, and ensures long-term retention. This section will explore why regular practice plays such a key role in building proficiency and confidence in various topics.
Here are a few reasons why practicing regularly is so important:
- Reinforces Core Concepts: Regular exercises help solidify foundational ideas, ensuring they become second nature. The more you practice, the more these principles will stick in your memory.
- Improves Problem-Solving Speed: Frequent practice increases your ability to solve problems more quickly and efficiently. As you encounter similar tasks, you’ll develop a faster and more intuitive approach.
- Enhances Understanding: Practice provides the opportunity to engage with problems in depth, allowing you to understand the underlying principles and strategies needed for successful problem solving.
- Builds Confidence: With each solved problem, your confidence grows. Over time, as you become more comfortable with different types of challenges, you’ll feel more prepared to tackle complex tasks.
In addition to these benefits, regular practice can also help you identify areas of weakness. By working through problems repeatedly, you can pinpoint specific concepts that require further attention and focus your study efforts more effectively.
Breaking Down Complex Problems with the Guide
When faced with a challenging problem, the key to solving it effectively is breaking it down into smaller, more manageable steps. This section will focus on strategies to simplify complex issues and how using the right resources can make the process smoother and more efficient.
Approaching Large Problems in Steps
Divide and Conquer: One of the most effective strategies is to divide a complex problem into smaller subproblems. By tackling each part individually, you can prevent feeling overwhelmed and make steady progress toward the solution. Each step should build upon the last, leading you toward the final result.
Using the Right Tools for Efficiency
Guided Solutions: Having access to a structured resource allows you to approach problems with a clear understanding of the necessary steps. It can serve as a reference point, providing insight into how to break down tasks and identify the critical elements needed for solving them.
For example: When solving a multi-step problem, you might begin by identifying the key information, then use this guide to help you through each calculation, ensuring nothing is overlooked.
By following a logical structure and using the right reference material, even the most complex problems can be tackled with confidence and efficiency.
Optimizing Your Study Routine

To achieve success in mastering any subject, it’s essential to approach your study sessions with a well-structured routine. This section will explore how to streamline your preparation, improve focus, and maximize learning efficiency. With the right strategies, you can make your study time more productive and ensure consistent progress.
Here are some tips for optimizing your study routine:
- Set Clear Goals: Start each session with specific objectives. Know exactly what concepts or problems you want to tackle. Having a clear focus will prevent you from getting distracted and ensure your efforts are directed towards meaningful progress.
- Break It Down: Instead of trying to learn everything at once, break down complex topics into smaller, more manageable sections. This approach will help you digest information better and prevent you from feeling overwhelmed.
- Consistency is Key: Regular practice is crucial for long-term retention. Set aside dedicated time each day to study, even if it’s just for a short period. Consistency helps reinforce concepts and improves memory.
- Mix It Up: Avoid studying the same material for hours at a time. Switch between different topics or types of problems to keep things fresh and engage different cognitive processes.
- Track Your Progress: Keep track of your achievements. Reviewing what you’ve mastered and identifying areas where you need more practice can give you a sense of accomplishment and motivate you to keep going.
By following these tips, you can create a study routine that enhances your understanding, increases retention, and helps you master challenging concepts efficiently.
Advanced Topics and Solutions
In any field of study, there comes a point where basic concepts need to be expanded upon to understand more complex ideas. This section explores advanced topics and the methods to solve intricate problems. Understanding these concepts is essential for progressing to a higher level of mastery and applying knowledge to real-world situations. With clear solutions and strategies, tackling these advanced challenges becomes achievable.
Exploring Complex Theorems
Advanced topics often involve applying foundational principles to new scenarios. One such area is the use of theorems that deal with shapes, angles, and spatial relationships. By building on simpler concepts, you can delve into more complex areas such as:
- The Pythagorean Theorem: A critical theorem for understanding relationships between the sides of right triangles, useful in various complex scenarios.
- Trigonometric Identities: The exploration of angles and the relationships between them can lead to more detailed solutions in real-world problems.
- Coordinate Geometry: Applying algebraic principles to geometric shapes allows for the study of properties like distance, midpoint, and slope.
Solving Advanced Problems
To tackle challenging problems, it is important to break them down into manageable parts. Here are some strategies to approach advanced exercises:
- Identify Patterns: Recognizing recurring relationships within a problem can provide clues for a solution.
- Utilize Proofs: Many advanced topics require logical reasoning and formal proofs. Ensuring each step is supported by a valid argument is crucial in reaching the correct solution.
- Practice with Variations: Once a concept is understood, practice applying it to different types of problems. This enhances comprehension and helps uncover deeper insights.
Mastering advanced topics is a key part of progressing in any mathematical discipline. With persistent practice and by focusing on solving complex problems, you can gain a deeper understanding and confidence in applying these skills.
Improving Skills with Practice
Mastering any subject requires consistent effort and focus, and this is especially true for the study of spatial relationships and mathematical problem-solving. Regular practice is key to strengthening your understanding and enhancing your ability to solve increasingly complex challenges. By working through a variety of problems, you solidify the concepts and techniques required for success.
The more you practice, the more you become familiar with different types of problems and the strategies needed to approach them. Developing a systematic approach and revisiting difficult problems can help reinforce your skills and build confidence. Whether you’re solving basic exercises or tackling more advanced questions, repetition and practice are critical for growth.
Here are some effective methods to enhance your skills:
- Work Through Varied Problems: By solving a wide range of problems, you expose yourself to different approaches and techniques, strengthening your ability to tackle challenges from multiple angles.
- Focus on Understanding, Not Memorization: It’s more beneficial to understand the underlying principles rather than just memorizing formulas. This will allow you to apply your knowledge flexibly in new situations.
- Review Mistakes: Reviewing errors and understanding why a solution didn’t work is an excellent way to learn. This helps to avoid similar mistakes in the future and deepens your understanding of the material.
With dedicated practice, your skills in problem-solving and logical reasoning will improve over time. This process of continuous learning not only increases your knowledge but also strengthens your confidence in applying these concepts in real-world situations.