
Effective learning in elementary education relies on understanding core concepts and applying problem-solving techniques. Students in the fifth level are introduced to more complex ideas that require clarity and practice. This guide is designed to assist learners in mastering foundational topics through clear and detailed solutions.
Unlocking solutions to various challenges is essential for academic progress. Whether it’s tackling word problems, understanding patterns, or exploring numerical relationships, having a reliable resource is crucial for success. This article provides a structured approach to the materials covered in the first two learning segments of the year.
By focusing on practical methods and offering step-by-step instructions, this guide aims to enhance comprehension and provide a clearer path through difficult exercises. Students will find valuable tips and strategies that will strengthen their understanding and help them achieve mastery in critical subjects.
Overview of Fifth Grade Learning
The journey through elementary education introduces students to a range of increasingly complex concepts, with a strong emphasis on problem-solving and logical thinking. In the fifth level, learners are expected to develop a deeper understanding of foundational topics that they will build on in the years ahead. The focus is not only on mastering basic skills but also on applying them to more challenging and real-world situations.
Core Areas of Study
This academic stage covers a broad spectrum of essential topics. From operations with fractions and decimals to understanding geometric shapes and their properties, students engage with a variety of exercises designed to strengthen their mathematical thinking. These subjects are carefully structured to foster both conceptual understanding and practical application.
Supporting Materials for Success
To support student learning, structured resources, including practice exercises and detailed explanations, are provided. These tools help learners to approach problems with confidence and develop critical thinking abilities that will serve them well in higher education. With the right support, students can navigate the challenges presented at this level and build a solid foundation for future success.
Module 1 Key Concepts Explained
The first segment of the curriculum introduces students to foundational topics that serve as the building blocks for more complex problem-solving skills. These concepts focus on helping learners develop a strong understanding of numerical relationships, operations, and the basic structures needed for further study. The goal is to provide a clear and structured approach to ensure that students are well-prepared for the challenges ahead.
Understanding Fractions and Decimals
One of the main areas of focus is working with fractions and decimals. Learners are encouraged to grasp the relationship between these two types of numbers and how to convert from one to the other. This concept is crucial for developing a strong sense of number sense, which will be applied in various scenarios throughout the year. Understanding operations with fractions and decimals lays the groundwork for solving more advanced problems involving these numbers.
Patterns and Relationships in Numbers
Another key concept explored in the first section is the identification and understanding of number patterns. Recognizing patterns is an essential skill, as it enables students to predict outcomes and make logical connections between different sets of numbers. This skill helps with the development of problem-solving strategies that can be applied in a wide range of situations.
Module 2 Key Concepts Overview
The second section of the curriculum expands upon the foundational concepts introduced earlier, focusing on more advanced operations and their real-world applications. The primary goal is to deepen students’ understanding of numbers and enhance their problem-solving abilities. This stage introduces more complex scenarios that require a solid grasp of the basic skills learned in the previous module.
Advanced Operations with Fractions
In this segment, learners focus on more complex operations involving fractions, including addition, subtraction, multiplication, and division. Understanding these operations is essential for solving real-life problems involving parts of a whole. Key points covered include:
- Adding and subtracting fractions with like denominators
- Multiplying fractions by whole numbers
- Converting improper fractions to mixed numbers and vice versa
Exploring Volume and Measurement

The concept of volume and measurement is also introduced in this section. Students learn how to calculate the volume of different shapes, understand units of measurement, and apply these skills to real-world problems. Some of the topics include:
- Measuring the volume of rectangular prisms
- Understanding and applying different units of volume
- Solving word problems involving volume
How to Use the Answer Key
The solution guide is an essential tool for reinforcing the learning process. It provides a way to check the work completed and understand the methods used to arrive at the correct answers. Using this guide effectively helps to improve comprehension and develop problem-solving skills by offering explanations for each step involved in the solution.
To make the most of the solution guide, it’s important to approach it as a learning tool rather than just a way to check results. First, attempt to solve the problems independently. Afterward, refer to the guide to verify your answers and understand the reasoning behind the steps. This approach ensures that you’re learning the correct methods and not just memorizing solutions.
| Step | Action | Purpose |
|---|---|---|
| 1 | Attempt the problems on your own | To apply learned concepts and practice problem-solving |
| 2 | Compare your answers with the guide | To check for accuracy and identify mistakes |
| 3 | Study the steps provided for each solution | To understand the reasoning and improve your skills |
Common Challenges in Fifth-Level Learning
As students advance to more complex topics, they often face a variety of challenges that can hinder their progress. The transition from simpler concepts to more abstract ones can be difficult, and understanding the underlying principles requires both patience and practice. Identifying these common obstacles early on allows learners to develop strategies to overcome them and strengthen their skills.
One of the most common challenges at this stage is mastering operations with fractions and decimals. The concepts of adding, subtracting, multiplying, and dividing fractions can be confusing, especially when students are asked to convert between improper fractions and mixed numbers. Similarly, working with decimal numbers often presents difficulties in terms of place value and performing calculations accurately.
Another challenge involves problem-solving, particularly when it comes to word problems. Students must learn how to translate real-world situations into mathematical operations, which can be a complex task. Understanding how to break down a problem into manageable steps and identify the relevant information is a skill that takes time to develop.
Strategies for Understanding Module 1

Mastering the concepts in the first section of the curriculum is crucial for building a strong foundation. To fully grasp the material, students need to approach each topic step by step, ensuring they understand the fundamental principles before moving on to more complex problems. A systematic approach, along with consistent practice, will help solidify the concepts and make learning more effective.
Break Down Complex Problems
One effective strategy is to break down challenging problems into smaller, more manageable parts. When faced with a difficult question, focus on one step at a time rather than trying to solve everything at once. This approach makes the problem less overwhelming and allows you to address each aspect methodically. For example, when working with fractions, start by identifying the denominator and numerator, and then proceed with the specific operation required.
Use Visual Aids to Reinforce Learning
Visual aids such as number lines, fraction bars, and diagrams can be incredibly helpful in understanding abstract concepts. These tools provide a concrete way to see relationships between numbers and operations. For instance, drawing a visual representation of a fraction can help clarify its value and make it easier to compare with others. Using such aids in practice exercises can enhance comprehension and retention of material.
Effective Study Tips for Module 2
To succeed in the second section of the curriculum, students need to adopt efficient study habits that focus on both understanding and application. This stage builds upon earlier concepts, requiring learners to expand their skills and tackle more complex problems. By following specific strategies, students can enhance their ability to grasp new topics and retain the knowledge necessary for mastery.
Active Practice and Review
Consistent practice is key when tackling more difficult topics. Simply reading through the material isn’t enough–students must actively engage with the problems, applying what they’ve learned to different scenarios. Regularly reviewing past exercises also helps reinforce concepts, ensuring they remain fresh in the mind. A well-rounded study routine should include:
| Activity | Purpose |
|---|---|
| Daily practice problems | Reinforce learned concepts and improve problem-solving speed |
| Weekly review sessions | Ensure retention of key ideas and correct any misunderstandings |
Collaborative Learning
Studying with peers can significantly enhance understanding, especially when tackling difficult problems. Group study sessions provide opportunities for discussion, allowing students to explain concepts to each other and gain different perspectives. Collaborative learning also helps to identify gaps in knowledge and allows for collective problem-solving. Whether through formal study groups or casual partnerships, learning with others is a great way to strengthen skills.
Detailed Solutions for Grade 5 Exercises

In this section, we break down the solutions to various exercises typically found in the curriculum for fifth-level students. The goal is to provide clear, step-by-step instructions that will help learners understand how to approach different types of problems. By carefully following these detailed explanations, students can gain a deeper understanding of the concepts and improve their problem-solving skills.
Each solution is presented with a logical progression of steps, ensuring that students can follow along and replicate the methods used to arrive at the correct answer. This approach not only clarifies the process but also reinforces the underlying principles that guide each operation, whether it’s working with fractions, decimals, or basic arithmetic operations.
Teacher’s Guide to Answer Keys
This section provides educators with a comprehensive guide to utilizing solution guides effectively in the classroom. The purpose of these guides is to offer teachers the tools necessary to support student learning and ensure accurate assessment of their progress. A well-structured solution guide not only helps in checking students’ work but also serves as a valuable resource for explaining the reasoning behind each step in a solution.
Teachers can use the solution guides to identify common errors and misconceptions, allowing them to address issues before they become barriers to further learning. Additionally, these guides provide insights into different strategies for solving problems, giving educators the flexibility to teach in ways that best suit their students’ needs. The guide can also be a helpful tool for discussing problem-solving techniques and encouraging critical thinking among students.
Breaking Down Module 1 Problems
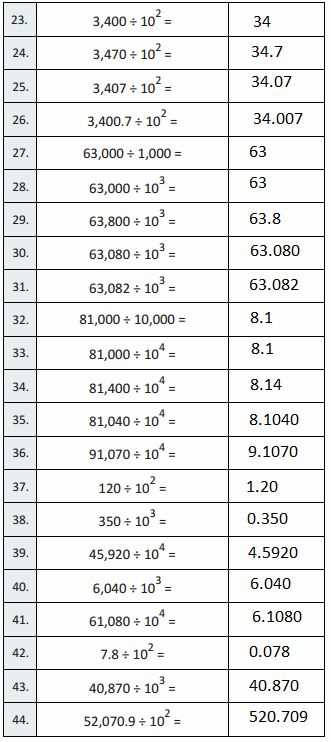
In this section, we focus on how to effectively approach and solve problems from the first unit of the curriculum. The key to mastering the content is breaking down each problem into smaller, manageable parts. By isolating each step and tackling one concept at a time, students can understand the underlying logic and develop the skills needed to solve more complex problems.
The process begins by carefully reading the problem and identifying the key information. Once the relevant data is recognized, students should focus on applying the appropriate operations or strategies. Taking the time to organize the information visually or through written notes can also help clarify the steps and reduce confusion.
It’s important to stay patient and methodical. When tackling problems that involve multiple steps, working through each stage incrementally helps prevent mistakes. Reviewing the solution after each step and cross-checking calculations ensures that the work is accurate and logical.
Step-by-Step Guide for Module 2
This section provides a detailed breakdown of how to approach and successfully complete the exercises in the second unit of the curriculum. The focus is on providing a clear, structured method for solving problems, which ensures students develop a deep understanding of the material. By following a step-by-step approach, learners can build confidence and improve their problem-solving abilities.
Understanding the Problem
The first step is to carefully read and analyze each problem. Identify the key elements, such as the numbers, operations, and any additional information that may affect the solution. Once the essential components are understood, it becomes easier to determine the correct approach. In some cases, drawing a quick sketch or organizing the data visually can aid in grasping the full scope of the problem.
Applying the Correct Strategy
After understanding the problem, the next step is to choose the appropriate method to solve it. Whether it’s working with fractions, decimals, or other types of calculations, selecting the right strategy is crucial. For example, if the problem involves division, students may benefit from using long division or a simpler estimation technique, depending on the context. Always remember to work through each step carefully, double-checking the calculations to ensure accuracy.
Importance of Practice in Learning
Reinforcing new concepts through consistent practice is a fundamental aspect of mastering any subject, particularly in areas that require logical thinking and problem-solving. Regular exercises help solidify the knowledge gained and enable students to become more confident in their abilities. By working through a variety of problems, learners are able to deepen their understanding and develop stronger skills that will serve them throughout their educational journey.
Building Strong Foundations

Practice allows students to build a strong foundation by repeatedly applying new methods in different contexts. The more students engage with the material, the more familiar they become with the steps and techniques involved. This repeated exposure helps them internalize the content, making it easier to recall and apply in future challenges.
Developing Problem-Solving Skills
Engaging in regular practice also enhances problem-solving abilities. By encountering a range of problem types, students develop a toolkit of strategies to handle various situations. This experience improves their critical thinking skills, enabling them to approach unfamiliar problems with greater ease and flexibility.
Benefits of Regular Practice

- Improves retention of key concepts
- Enhances speed and accuracy in solving problems
- Builds confidence through mastering difficult topics
- Fosters a growth mindset, encouraging persistence
In short, practicing regularly is not just about repeating exercises, but about reinforcing understanding and building long-term success in learning. Each practice session contributes to the overall development of a student’s abilities, paving the way for academic growth and mastery.
Review of Key Skills in Grade 5

In this section, we will highlight some of the essential skills students need to master in the fifth year of their learning journey. These skills not only form the foundation for more advanced topics but also help students gain confidence and improve their problem-solving abilities. Mastering these key competencies is crucial for academic success and for applying knowledge to real-world situations.
Core Concepts to Focus On
- Understanding Fractions: Students should be comfortable with comparing, adding, subtracting, multiplying, and dividing fractions. The ability to work with fractions lays the groundwork for more complex operations later on.
- Decimals: Understanding how decimals relate to fractions is important, particularly when performing operations involving money, measurements, or other practical contexts.
- Measurement: Learning how to convert units of measurement, such as length, volume, and weight, helps students solve real-life problems and understand scientific concepts.
- Data Interpretation: Analyzing charts, graphs, and tables is essential for understanding data and making informed decisions based on that information.
- Basic Geometry: Concepts like area, perimeter, and understanding geometric shapes play an important role in various subjects, including science and engineering.
Building Strong Foundations for Future Learning
Mastering these essential skills in the fifth year of study enables students to move on to more complex topics with ease. A solid understanding of foundational concepts allows for smoother transitions into higher-level learning, and sets students up for success in their academic journey.
Improving Problem Solving Skills
Enhancing problem-solving skills is vital for academic success and personal growth. These skills not only help students approach complex tasks with confidence but also prepare them for real-life challenges. Developing strong strategies for problem-solving encourages critical thinking, creativity, and persistence–skills that can be applied in various disciplines and everyday situations.
Key Approaches to Strengthening Problem Solving Abilities
To become more proficient at solving problems, students can adopt several strategies. These strategies guide them through the process of analyzing and tackling challenges effectively.
| Strategy | Description |
|---|---|
| Break the Problem Down | Start by dividing a complex problem into smaller, manageable parts. This approach makes it easier to focus on one aspect at a time, reducing overwhelm. |
| Understand the Question | Carefully read and comprehend the problem. Identifying what is being asked is crucial to formulating the right approach. |
| Plan the Solution | Think about the steps needed to solve the problem. Planning ahead saves time and minimizes errors. |
| Test and Revise | After finding a potential solution, test it and assess whether it solves the problem as expected. If not, revise the approach and try again. |
| Learn from Mistakes | Mistakes are part of the learning process. Analyzing errors helps improve strategies and avoid similar issues in the future. |
By regularly practicing these strategies, students can improve their problem-solving abilities and gain a deeper understanding of the concepts they are learning. Consistent application of these methods builds confidence and strengthens the mental framework needed to tackle even the most challenging problems.
How to Check Your Work
Verifying your results is an essential part of the problem-solving process. It ensures that the solutions you arrive at are correct and helps identify any mistakes that may have been made along the way. By systematically reviewing your work, you can increase the accuracy of your answers and improve your understanding of the process.
Checking your work involves a few key strategies that can help ensure the integrity of your results. Whether you’re solving a complex problem or completing a simple task, following a clear process can prevent errors and build confidence in your solutions.
Step-by-Step Process for Verifying Results
Follow these steps to review and confirm your work:
- Review Each Step – Go over each part of your solution carefully. Check for any skipped steps or incorrect calculations that might have been overlooked during the initial attempt.
- Use Alternative Methods – Try solving the problem in a different way. If the second method gives the same result, it’s likely that your original solution is correct.
- Check Units and Labels – Make sure that all measurements, units, and labels are consistent and correct. This is especially important when working with quantities or values that require units of measurement.
- Recalculate Key Numbers – Double-check critical calculations to ensure there were no mistakes. Use a calculator or a different method to verify your work.
- Compare with the Expected Outcome – If possible, compare your solution with known or expected outcomes. This can provide a useful benchmark for determining whether your work is on track.
By following these simple checks, you can avoid common mistakes and ensure that your work is accurate. Regularly reviewing your work also promotes a better understanding of the concepts involved, helping you learn more effectively in the long term.
Additional Resources for Effective Learning
Accessing supplementary materials can greatly enhance your learning experience. Whether you’re reviewing previous concepts or exploring new ones, these resources provide extra support to reinforce your understanding and offer different perspectives on problem-solving techniques. There are various tools available that cater to different learning styles, helping you grasp difficult concepts more effectively.
In this section, we explore a variety of additional resources that can support your educational journey, from online platforms to printed materials. These resources are designed to complement the curriculum and help you deepen your understanding of essential concepts.
Online Platforms and Websites
Several websites provide interactive tools, video tutorials, and practice exercises that can help solidify your knowledge. Some of the most useful online platforms include:
- Khan Academy: A comprehensive platform offering video lessons and exercises that cover a wide range of topics. It’s particularly helpful for reinforcing concepts learned in the classroom.
- IXL: An educational website offering interactive practice problems in various subjects. It tracks progress and adapts questions to the learner’s level.
- Prodigy: A fun, game-based learning platform that engages students while providing practice opportunities for various subjects, including problem-solving and critical thinking skills.
Books and Printed Materials
If you prefer offline learning, books and workbooks can provide valuable practice and in-depth explanations. Some recommended options include:
- Math Workbooks: Available in most bookstores, these workbooks focus on reinforcing key concepts and offer ample exercises for practice.
- Conceptual Books: Books that explain core principles of logic and problem-solving in a way that is accessible and engaging for learners of all levels.
These additional resources can be extremely helpful in reinforcing your learning, offering further explanations, and providing more practice opportunities. By using a variety of materials, you can approach each concept from different angles, helping you become more confident and proficient in your studies.