
In this section, we explore important concepts and provide detailed solutions to help students navigate through complex learning topics. Mastering these skills is crucial for building a strong foundation in essential areas of study. Whether you’re tackling challenging problems or looking for a deeper understanding, this guide offers step-by-step support.
Comprehending each problem type is a vital part of advancing through the curriculum. By breaking down the methods and techniques used in solving various exercises, we aim to simplify even the most difficult tasks. With clear explanations and structured approaches, learners will find themselves better equipped to approach similar challenges in the future.
Additionally, avoiding common pitfalls is key to making progress. Recognizing frequent errors and learning how to correct them ensures students not only complete their assignments accurately but also grasp the underlying principles. This section is designed to assist in that process, helping students refine their problem-solving abilities.
Eureka Math Grade 5 Module 6 Answer Key
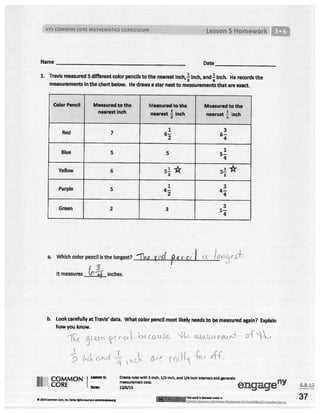
This section provides solutions and insights for completing the exercises and understanding the underlying concepts. By reviewing each solution in detail, students can enhance their comprehension of key mathematical principles and improve their problem-solving skills.
Step-by-Step Solutions
Each problem in this section is addressed with a clear, concise explanation. Understanding the methodology behind each solution ensures that students can apply similar strategies to new problems.
- Understanding Fractions: Key techniques for working with fractions are demonstrated, including simplifying, comparing, and performing operations on fractions.
- Problem-Solving Approaches: The section outlines effective methods for tackling word problems and complex calculations, breaking down each step for clarity.
- Visualizing Concepts: Diagrams and visual aids are incorporated to support students in grasping abstract concepts in a more tangible way.
Common Pitfalls and How to Avoid Them
Students often encounter similar challenges when working through the exercises. Identifying these common errors and learning strategies to avoid them is essential for improving accuracy and efficiency.
- Misinterpretation of Word Problems: Carefully read each question to avoid making assumptions and ensure a clear understanding of what is being asked.
- Incorrect Fraction Operations: Double-check calculations involving fractions to ensure the correct methods, such as finding common denominators, are used.
- Skipping Steps: Avoid jumping directly to the final answer. Ensure all intermediate steps are clearly shown to prevent errors.
Understanding Eureka Math Grade 5
This section explores the essential concepts and skills that are introduced at this stage of learning. It focuses on building a strong foundation in key areas of arithmetic, problem-solving, and logical reasoning. The goal is to ensure that students not only understand how to solve problems but also grasp the principles behind the calculations and strategies.
As students progress through these exercises, they will develop a deeper understanding of fractions, ratios, and other critical concepts. The approach emphasizes hands-on learning, encouraging students to engage with the material through practical examples and step-by-step guidance. This method fosters both competence and confidence, providing students with the tools they need to succeed in more advanced topics.
Key Concepts in Module 6
This section delves into the fundamental ideas covered in this part of the curriculum. Students will explore a variety of essential concepts, each building on previous knowledge and designed to deepen their understanding of mathematical operations and problem-solving techniques. Mastering these concepts is crucial for success in future studies and everyday applications.
- Fractions: A deeper focus on operations with fractions, including addition, subtraction, multiplication, and division. Students learn to handle fractions in different contexts, including word problems.
- Decimal Equivalence: Understanding the relationship between fractions and decimals, and how to convert between them to simplify calculations and comparisons.
- Word Problems: Strategies for interpreting and solving real-world problems presented in narrative form. These problems require careful reading and application of mathematical principles to find the solution.
- Measurement: An introduction to different units of measurement, including length, weight, and volume, with an emphasis on converting between units.
By focusing on these key areas, students can solidify their comprehension and gain the skills needed to approach more advanced topics with confidence.
How to Use the Answer Key
Using a solution guide effectively can significantly improve your understanding of challenging topics. This section explains how to make the most of the provided solutions, helping you learn not only the correct answers but also the methods and strategies used to solve each problem.
Steps for Effective Use
To maximize the benefit of the solutions, follow these steps:
- Review Each Step: Don’t just look at the final answer. Study each step carefully to understand the logic and operations involved in reaching the solution.
- Compare Your Work: After attempting a problem on your own, check your method against the solution. This will help you identify any errors in your approach and improve your problem-solving skills.
- Analyze Mistakes: If your solution differs from the provided one, take time to analyze where you went wrong. Correcting your mistakes will enhance your understanding and prevent future errors.
- Practice Independently: Use the solutions as a reference but continue practicing similar problems without looking at the guide. This will strengthen your ability to solve problems on your own.
Additional Tips for Success
- Take Notes: Jot down key methods or tricks you find helpful while reviewing the solutions. These notes can serve as a quick reference for future problems.
- Work with a Study Partner: Discuss the solutions with a classmate or tutor. Talking through the steps can provide new insights and reinforce learning.
Step-by-Step Guide to Module 6
This guide offers a structured approach to tackling the exercises and concepts covered in this section. By following each step, students can break down complex problems into manageable tasks, improving both their understanding and their ability to apply key concepts. Each step builds upon the previous one, ensuring a solid grasp of the material.
Understanding the Core Concepts
Before diving into the exercises, it’s important to familiarize yourself with the fundamental ideas. Take time to understand how the various concepts connect to each other, whether it’s working with fractions, performing operations, or solving real-world problems. A clear understanding of the basics sets the foundation for tackling more complex tasks.
Step-by-Step Process for Solving Problems

Follow these steps for solving problems effectively:
- Read the Problem Carefully: Take your time to understand what the question is asking before jumping to a solution. This helps prevent mistakes caused by misinterpretation.
- Identify Key Information: Highlight the important numbers, operations, and instructions within the problem. This makes it easier to focus on the necessary steps.
- Choose the Right Strategy: Based on the problem type, decide which method or formula you need to apply. This could include operations like addition, subtraction, multiplication, or division.
- Work Through the Steps: Break the problem down into smaller, more manageable parts. Complete each part before moving on to the next to avoid confusion.
- Check Your Work: Once you’ve reached a solution, go back and verify your steps to make sure there are no errors. Double-checking your work helps ensure accuracy.
Common Challenges in Module 6
As students work through this section, they often encounter a variety of challenges that can make understanding the material more difficult. These difficulties can arise from a lack of familiarity with specific concepts or the complexity of the problem-solving techniques required. By identifying these common obstacles, students can develop strategies to overcome them and strengthen their skills.
Understanding Fractions and Decimals
One of the most common challenges is working with fractions and decimals, especially when it comes to performing operations or converting between them. Many students struggle with finding common denominators, simplifying fractions, and comparing values. This can lead to confusion when solving problems that involve both fractions and decimals.
- Converting Fractions to Decimals: It’s important to practice converting fractions to decimals and vice versa. Understanding this relationship helps simplify problems and makes calculations easier.
- Adding and Subtracting Fractions: Fractions with different denominators require special attention. Students need to master finding a common denominator before performing operations.
Interpreting Word Problems
Word problems can often be a source of frustration. The key to solving them is carefully reading and extracting the necessary information. Many students find it challenging to identify what is being asked and how to translate the narrative into a solvable problem.
- Identifying Relevant Information: Pay close attention to the details given in the problem. Highlight or underline the important numbers and keywords that will guide you to the solution.
- Choosing the Correct Operations: Word problems often require multiple steps and different operations. It’s essential to determine which operations are needed at each step to reach the correct answer.
Tips for Solving Math Problems

Solving mathematical problems requires both a clear understanding of the concepts and a strategic approach. By following certain techniques, students can work more efficiently and effectively, building their confidence as they tackle increasingly complex tasks. These tips can help improve problem-solving skills and minimize errors along the way.
- Break Down the Problem: Start by dividing complex problems into smaller, more manageable parts. This helps simplify the task and allows you to focus on one step at a time.
- Understand the Question: Before jumping into calculations, carefully read the problem to ensure you understand what is being asked. Identifying the key information is crucial for determining the correct approach.
- Choose the Right Method: Select the appropriate strategy for solving the problem. Whether it’s addition, subtraction, multiplication, or division, make sure the chosen method aligns with the problem’s requirements.
- Use Visual Aids: Drawing diagrams, charts, or number lines can help visualize the problem and make abstract concepts more tangible. This is especially useful when dealing with fractions, ratios, or measurements.
- Double-Check Your Work: Always review your calculations before finalizing your answer. Look for simple mistakes such as misplacing a decimal or incorrectly performing an operation.
- Practice Regularly: The more problems you solve, the better you become at recognizing patterns and applying solutions. Regular practice helps reinforce concepts and enhances problem-solving speed.
How to Improve Math Skills
Improving your ability to solve mathematical problems takes practice, focus, and a willingness to tackle challenges. Strengthening these skills involves understanding core principles, applying techniques regularly, and addressing areas where you face difficulties. With the right strategies, anyone can enhance their problem-solving abilities and boost their confidence in dealing with numbers.
- Practice Regularly: Consistent practice is key to mastering mathematical concepts. Set aside time each day to solve problems, review new concepts, and reinforce your understanding.
- Master Basic Concepts: Ensure you have a solid grasp of fundamental operations such as addition, subtraction, multiplication, and division. Building a strong foundation is crucial for tackling more complex problems.
- Work on Mental Math: Try solving problems in your head to improve your speed and accuracy. Mental calculations help you become more flexible with numbers and develop problem-solving strategies.
- Use Resources and Tools: Take advantage of educational tools, such as practice books, online tutorials, and worksheets. These resources can provide explanations and examples to clarify difficult topics.
- Break Down Problems: When faced with a challenging problem, break it down into smaller, more manageable parts. Solving each part step by step makes complex problems easier to handle.
- Seek Help When Needed: If you struggle with a particular topic, don’t hesitate to ask for help from teachers, classmates, or tutors. Getting a fresh perspective can help clarify difficult concepts.
Exploring Module 6 Practice Problems
Practice problems are essential for reinforcing the concepts and strategies learned in any lesson. In this section, we will explore various exercises that help deepen your understanding of the material. By working through these problems step by step, you can strengthen your problem-solving skills and gain more confidence in applying the learned techniques to real-world situations.
Types of Problems in This Section
This section contains a wide variety of problem types that target different skills. Some problems focus on numerical operations, while others require logical reasoning and application of mathematical concepts. By practicing each type, you can build versatility and adaptability in solving complex tasks.
- Arithmetic Operations: These problems involve basic operations like addition, subtraction, multiplication, and division. They help improve fluency with numbers.
- Word Problems: These problems test your ability to translate real-life scenarios into mathematical solutions. They often require careful reading and multiple steps to solve.
- Fraction and Decimal Operations: Expect to encounter problems involving fractions and decimals. These exercises focus on performing operations and conversions between these two forms.
How to Tackle the Problems Effectively
To solve these practice problems efficiently, follow these tips:
- Read the problem carefully: Understand what is being asked before jumping into calculations.
- Identify important information: Highlight or underline key numbers and terms to avoid missing essential details.
- Break down the steps: Solve the problem step by step to ensure accuracy and prevent confusion.
- Check your solution: Always verify your answer before finalizing it to ensure no mistakes were made.
Focus Areas for Grade 5 Students
In fifth grade, students are introduced to more complex concepts that build on the foundational knowledge they’ve acquired in earlier years. The focus shifts to developing a deeper understanding of key areas, which are essential for academic growth and future success. By concentrating on these focus areas, students can master important skills that will serve them well in more advanced studies.
- Understanding Fractions and Decimals: Fifth graders should strengthen their ability to work with fractions and decimals, including operations like addition, subtraction, multiplication, and division. Mastery of these concepts is crucial for more advanced topics in later grades.
- Problem Solving with Multi-Step Processes: At this stage, students are expected to solve problems that require multiple steps. This encourages logical thinking and enhances their ability to break down complex problems into manageable parts.
- Developing Measurement Skills: Students should gain a solid understanding of units of measurement, both in the metric and customary systems. This includes converting between different units and applying them in real-life scenarios.
- Mastering Multiplication and Division: Strengthening skills in multiplication and division, especially with larger numbers, is a key area of focus. This helps students improve their fluency and efficiency in performing arithmetic operations.
- Geometric Concepts: An understanding of basic geometric shapes and their properties is important at this level. Students will explore concepts such as perimeter, area, and volume, and apply them in practical situations.
Understanding Fractions in Module 6
Fractions are a crucial concept for students to grasp as they represent parts of a whole. In this section, the focus is on understanding how fractions work, how to perform operations with them, and how to apply these skills to solve various problems. Mastery of fractions forms the foundation for more advanced topics in mathematics, making it an essential area of study.
Key Concepts in Fraction Understanding
Students are introduced to a variety of important concepts related to fractions. These include:
- Equivalence of Fractions: Recognizing that different fractions can represent the same value is an important skill. Students learn to simplify fractions and compare them based on their equivalency.
- Adding and Subtracting Fractions: Understanding how to add and subtract fractions, especially those with unlike denominators, is an important step in building fraction fluency.
- Multiplying Fractions: Multiplying fractions involves multiplying the numerators and denominators, and students learn how to apply this operation in both theoretical and real-life scenarios.
Practical Applications of Fractions
Fractions appear in everyday life, and understanding them allows students to solve practical problems, such as dividing a pizza into equal parts or measuring ingredients in recipes. These real-world connections help students see the relevance of what they are learning and strengthen their skills in working with fractions.
Word Problems and Strategies
Word problems are an important way to apply mathematical concepts to real-life situations. These problems require students to interpret written information and translate it into mathematical operations. The ability to solve word problems strengthens critical thinking skills and helps students see the practical value of the concepts they are learning.
Common Strategies for Solving Word Problems

There are several strategies that students can use to solve word problems effectively:
- Read the problem carefully: It’s important to understand what the problem is asking before attempting to solve it.
- Identify key information: Highlight or underline the relevant numbers, terms, and operations needed to solve the problem.
- Translate words into numbers: Convert the worded information into mathematical expressions or equations.
- Break the problem into smaller steps: Complex word problems can often be solved by breaking them down into simpler, more manageable parts.
- Check your work: After solving the problem, review the steps and calculations to ensure the solution is correct.
Example of Solving a Word Problem
| Problem | Steps | Solution |
|---|---|---|
| A store sells 3 apples for $2. How much would 9 apples cost? |
|
The cost of 9 apples is $6. |
By practicing these strategies, students will improve their ability to solve word problems and become more confident in applying mathematical thinking to everyday scenarios.
How to Prepare for Module 6 Assessments
Effective preparation for assessments is key to performing well and building a strong foundation for future learning. By reviewing key concepts, practicing problem-solving techniques, and managing study time efficiently, students can approach their tests with confidence. This section provides helpful tips and strategies to ensure success during evaluations related to the concepts learned in this section.
Steps to Prepare for the Assessment
To prepare for assessments, follow these essential steps:
- Review the content: Go over all the major topics covered in the lessons, ensuring understanding of each concept before the test.
- Practice problems: Solve practice exercises that reflect the types of problems likely to appear on the assessment.
- Work with study groups: Collaborate with classmates to review and discuss challenging topics, as this can help reinforce understanding.
- Ask for help: If any concepts are unclear, seek clarification from the teacher or use additional resources for support.
- Take regular breaks: Avoid cramming by taking breaks during study sessions to keep your mind fresh and focused.
Example of Effective Study Plan
The following table outlines a sample study plan leading up to an assessment, which can help you stay organized and manage your time efficiently:
| Day | Topics to Review | Practice Exercises |
|---|---|---|
| Day 1 | Fractions and Equivalent Fractions | Complete problems on simplifying fractions and finding equivalent forms. |
| Day 2 | Adding and Subtracting Fractions | Solve addition and subtraction problems involving fractions with different denominators. |
| Day 3 | Multiplying Fractions | Practice multiplication of fractions, including word problems. |
| Day 4 | Review of Word Problems | Work through a series of word problems related to fractions. |
| Day 5 | Final Review and Practice Test | Take a practice test covering all major topics to check your understanding. |
By following a structured study plan, students can feel well-prepared and confident for their assessments, ensuring they can effectively demonstrate their knowledge and problem-solving abilities.
Key Formulas and Methods
Understanding the essential formulas and techniques is crucial for solving problems effectively. These tools provide a systematic approach to tackling various types of problems, ensuring that students can apply the right strategies at the right time. In this section, we will explore the primary methods and formulas used to solve common problems and improve problem-solving skills.
Essential Formulas for Problem Solving

Here are some of the most important formulas to remember when working through challenges:
- Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, first find a common denominator, then adjust the fractions accordingly.
- Multiplication of Fractions: To multiply fractions, multiply the numerators together and the denominators together. Simplify the result if needed.
- Dividing Fractions: To divide fractions, multiply the first fraction by the reciprocal of the second fraction.
- Finding Equivalent Fractions: Multiply both the numerator and denominator by the same number to find an equivalent fraction.
- Converting Fractions to Decimals: Divide the numerator by the denominator to convert a fraction into its decimal form.
Problem-Solving Methods

Here are some effective methods for solving problems that require critical thinking and step-by-step calculations:
- Break Down the Problem: Start by carefully reading the problem and identifying the key information. Write down what is given and what needs to be found.
- Use Visual Aids: Draw diagrams or use number lines to visualize fractions or relationships between numbers, which can often make complex problems easier to understand.
- Work Backwards: In some cases, working backward from the solution can help find the correct answer. Start from the desired outcome and reverse the steps.
- Check Your Work: After solving the problem, always revisit your solution to ensure no mistakes were made. Double-check your calculations and reasoning.
Mastering these formulas and methods allows students to confidently solve problems, improve their skills, and achieve better outcomes in their assessments and future learning.
Visual Aids in Learning Module 6
Using visual aids is an effective approach to understanding complex concepts, especially when dealing with abstract ideas. Diagrams, charts, and visual representations can help students grasp the relationships between numbers, fractions, and geometric figures more easily. This section explores the different types of visual tools that can support learning in this area.
Types of Visual Aids
Various types of visual aids can be incorporated into lessons to enhance understanding:
- Fraction Models: Diagrams such as pie charts or bar models visually represent fractions, helping students compare and visualize parts of a whole.
- Number Lines: A number line helps students see the relative size of fractions, decimals, or integers and understand their positions on a continuum.
- Area Models: These are used to show the product of fractions or division, giving students a tangible representation of operations.
- Visual Word Problems: Sometimes a diagram can clarify the meaning of word problems by showing relationships and quantities, making it easier to identify key information.
Benefits of Using Visual Aids
Visual tools offer several advantages when tackling mathematical challenges:
- Clarification of Concepts: When students can visually see problems represented, it’s easier to comprehend the concepts behind them.
- Enhanced Memory Retention: Visual aids help reinforce concepts, allowing students to remember and recall information more effectively.
- Engagement: Students are often more engaged and motivated when they are presented with interactive visual tools, keeping them focused on the lesson.
- Problem-Solving Support: Visual aids can break down complex problems into manageable steps, making it easier to follow through on solutions.
Incorporating visual aids into lessons not only supports comprehension but also makes learning more interactive and enjoyable, providing students with the tools they need to succeed.
Common Mistakes to Avoid in Module 6
In the process of learning complex concepts, it’s easy for students to make mistakes that hinder their understanding. Being aware of common pitfalls can help prevent frustration and promote more accurate problem-solving. This section highlights the most frequent errors students encounter and offers advice on how to avoid them.
Common Errors in Fraction Operations
Fraction-related tasks can often lead to confusion. Here are some common mistakes to watch out for:
- Misunderstanding Fraction Simplification: Students sometimes forget to simplify fractions after performing operations, which can lead to incorrect results.
- Incorrect Fraction Addition/Subtraction: Adding or subtracting fractions without making sure the denominators are the same is a frequent mistake. Always check that the fractions have a common denominator before performing these operations.
- Confusing Numerators and Denominators: It’s common for students to swap the numerator and denominator when working with fractions. Always double-check the structure of the fraction.
Misinterpretation of Word Problems
Word problems require students to carefully read and analyze the information. Common mistakes in this area include:
- Skipping Key Information: Sometimes, students overlook important details in word problems, leading to incorrect conclusions. It’s essential to read each problem thoroughly and identify all the necessary data.
- Incorrect Setup of Equations: Setting up the wrong equation or operation based on the problem’s context is another common mistake. Ensure that the relationship between the numbers is correctly translated into an equation.
- Failure to Check Work: After solving a problem, students may fail to revisit their solution, which can result in overlooked errors. Always take the time to verify calculations and logic before finalizing an answer.
Being mindful of these mistakes and implementing strategies to avoid them can lead to more successful learning experiences and a better understanding of the subject matter.