
In the second year of elementary education, students encounter increasingly complex challenges in their studies, especially in problem-solving. Understanding key concepts and learning how to approach various exercises is crucial for their success. This section provides valuable resources and solutions to help children navigate through these academic hurdles effectively.
By focusing on critical thinking and step-by-step strategies, children develop essential skills for overcoming difficulties they may face during their lessons. This guide is designed to enhance comprehension and provide practical approaches that students can use to solve problems independently. It ensures that learners build confidence and mastery in the topics at hand.
Parents and educators will also find this guide helpful, offering detailed solutions and explanations that support the learning process. With clear instructions and accessible techniques, this section aims to make the learning experience smoother and more enjoyable for both students and their mentors.
Eureka Math Grade 2 Module 4 Answer Key
This section provides a detailed guide to solving key problems encountered during the second year of elementary education. Students are introduced to a variety of concepts that build upon prior knowledge, and understanding how to approach these challenges is essential for mastery. By reviewing the correct solutions and methods, learners can enhance their problem-solving skills and strengthen their understanding of the material.
Steps for Solving Problems Effectively
Understanding the proper steps for tackling problems is fundamental. Here are the key approaches to ensure a clear path to solving exercises:
- Carefully read the problem and identify the main objective.
- Break down complex questions into smaller, more manageable parts.
- Apply the learned techniques step-by-step to reach a solution.
- Double-check the work to confirm accuracy and clarity.
Common Areas of Difficulty
As students progress, they may encounter some challenges. Here are a few areas where learners often need extra attention:
- Understanding word problems and identifying the right operations.
- Maintaining focus on multi-step exercises.
- Applying reasoning to solve more complex tasks.
With patience and practice, students can overcome these obstacles and gain confidence in their abilities. By using this guide, learners and educators can ensure consistent progress and a thorough understanding of all the concepts covered in this section.
Overview of Eureka Math Grade 2
The second year of elementary school focuses on building a strong foundation in key academic concepts. This stage is designed to help students advance their understanding of essential topics and develop problem-solving abilities. The approach emphasizes a deep comprehension of fundamental principles, enabling learners to tackle increasingly complex tasks with confidence.
Core Areas of Study

Throughout the year, students explore a variety of subjects that enhance their cognitive development. Key areas include:
- Basic arithmetic and number relationships
- Understanding measurement and data
- Introduction to simple geometric concepts
- Strengthening reasoning and logical thinking skills
Learning Approach and Support
In this stage, students are encouraged to think critically and apply their knowledge in different contexts. Teachers and parents play a crucial role by offering guidance and support as students work through new challenges. Resources, such as practice exercises and solution guides, help reinforce the learning process and ensure that students stay on track with their academic development.
Understanding Module 4 Concepts
The fourth section of the second-year curriculum focuses on strengthening students’ abilities to solve more advanced exercises and deepen their understanding of critical topics. The concepts introduced build upon earlier lessons and are designed to encourage logical thinking and problem-solving. Mastery of these ideas provides a strong foundation for tackling increasingly complex challenges in future lessons.
Key Learning Goals
This section introduces several important concepts that students need to grasp for further academic success. The key objectives include:
- Enhancing number sense and working with larger values
- Understanding relationships between different mathematical operations
- Mastering strategies for solving word problems
- Exploring the concept of measurement and comparison
Building on Previous Knowledge

In this stage, learners are expected to apply the foundational knowledge they’ve acquired in earlier lessons to new and more challenging problems. The exercises are designed to stretch students’ thinking and improve their ability to make connections between different concepts. This gradual progression ensures that learners gain confidence as they continue to advance through their studies.
Key Topics Covered in Module 4
In this section, students encounter a range of essential concepts that help them further develop their problem-solving skills. These topics build on previous knowledge and introduce more complex ideas, preparing learners for future academic challenges. The focus is on reinforcing understanding while fostering the ability to approach different types of problems with confidence.
Among the most important topics covered are:
- Advanced strategies for addition and subtraction
- Understanding the relationship between numbers and their place value
- Working with measurement units and comparing different values
- Solving multi-step word problems that require logical reasoning
- Exploring simple geometric shapes and their properties
These topics are designed to help students connect abstract concepts to real-life situations, allowing them to see the practical applications of what they are learning. As students engage with these lessons, they will gain a deeper understanding of both foundational skills and more advanced techniques.
How to Use the Answer Key Effectively
Having access to a solution guide can significantly improve understanding and retention when working through academic exercises. However, it’s important to use this resource strategically to reinforce learning rather than just obtaining quick answers. The goal is to develop problem-solving skills and reinforce the concepts learned, ensuring that students build a deeper comprehension of the material.
Approach to Using Solutions
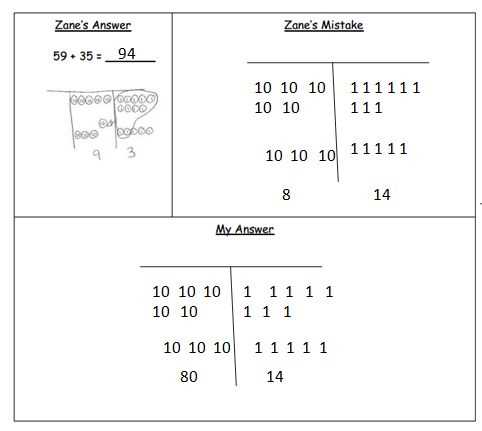
Here are a few tips for using the guide effectively:
- Attempt to solve the problem independently before checking the solution.
- If the answer doesn’t match, analyze the steps and identify where the error occurred.
- Focus on understanding the reasoning behind each solution, not just the final result.
- Use the solution guide as a tool to clarify concepts and strategies, not as a shortcut to bypass thinking.
Benefits of Correct Usage
When used properly, the solution guide helps reinforce critical thinking and analytical skills. Students can improve their approach to similar problems, correct mistakes, and reinforce concepts they may have missed. Here’s how the solution guide can help in different scenarios:
| Scenario | How to Use the Guide |
|---|---|
| Solving word problems | Review the steps and focus on the strategies used to break down the problem. |
| Working with numbers | Ensure you understand the steps taken to solve equations and verify the logic used. |
| Understanding geometry concepts | Check the reasoning behind how shapes are analyzed and the methods for comparison. |
By following these guidelines, students can ensure they are getting the most out of the resources available to them and advancing their understanding in a meaningful way.
Step-by-Step Solutions for Grade 2
Providing detailed, step-by-step solutions helps students better understand the processes required to solve problems. This approach not only reinforces the correct methods but also builds confidence as learners see how each task is tackled from start to finish. Breaking down each exercise into manageable steps ensures that complex concepts are made accessible and that students can follow along with ease.
Breaking Down Complex Problems

When solving a problem, it’s essential to break it down into smaller, more manageable parts. Here’s a general approach to tackle each exercise:
- Read the problem carefully to understand what is being asked.
- Identify any important information or numbers provided in the problem.
- Choose the appropriate operation(s) based on the information.
- Work through the steps in a logical order, ensuring each action is clear.
- Double-check the final result to confirm the solution is correct.
Applying Strategies for Success
Students can apply different strategies depending on the nature of the problem. Whether it’s solving a word problem, working with numbers, or understanding a new concept, the following steps can be applied across different types of exercises:
- Use drawings or diagrams to visualize the problem.
- Practice mental math skills to improve speed and accuracy.
- Revisit earlier lessons to connect new ideas with what has already been learned.
By following these steps, learners can approach each task methodically, reducing the chances of mistakes and strengthening their problem-solving skills over time.
Common Challenges in Module 4
As students progress through the curriculum, they often face certain challenges that can make some exercises more difficult to understand and solve. Recognizing these common obstacles early on can help learners develop effective strategies to overcome them. In this section, we will explore some of the typical difficulties encountered in this phase of learning and provide suggestions for how to address them.
Difficulty with Word Problems
One of the most common challenges is understanding and solving word problems. These exercises require students to carefully read and interpret the information before deciding which mathematical operations to use. Often, the complexity lies in identifying what the problem is asking and how to approach the solution logically. To tackle this challenge:
- Encourage students to underline or highlight key information in the problem.
- Teach them to break the problem into smaller, simpler parts.
- Practice solving word problems regularly to build confidence and familiarity with different scenarios.
Struggling with Place Value and Number Relationships
Another area where students often face difficulties is with understanding place value and the relationships between numbers. Concepts like comparing numbers, regrouping, and recognizing patterns can be confusing. To help students master this area:
- Use visual aids such as number lines or place value charts.
- Incorporate hands-on activities with physical objects like counters or blocks to make abstract concepts more tangible.
- Provide plenty of practice exercises that gradually increase in complexity to help reinforce these ideas.
By addressing these common challenges with targeted strategies and consistent practice, students can gain a stronger grasp of the material and build the confidence they need to succeed in this phase of learning.
Support for Parents and Teachers
Parents and teachers play a crucial role in helping students navigate through their learning journey, especially when new concepts become challenging. Offering the right kind of support can make a significant difference in how students engage with the material and build confidence in their abilities. This section provides practical tips and strategies for both parents and teachers to support students in mastering the topics introduced during this stage of learning.
Guidance for Parents
Parents can be instrumental in reinforcing what students learn in class. Providing a supportive home environment helps students feel more confident as they tackle their assignments. Here are some ways parents can assist:
- Establish a quiet, dedicated space for learning where children can focus without distractions.
- Encourage children to verbalize their thought process while solving problems to help solidify their understanding.
- Be patient and offer positive reinforcement when children make progress, even if it’s small.
- Use real-life examples to make concepts more relatable, such as measuring ingredients while cooking or comparing prices while shopping.
Tips for Teachers
For teachers, creating an engaging and supportive classroom environment is essential to fostering student success. Here are several strategies to help students grasp complex concepts:
- Incorporate interactive activities and hands-on learning to make abstract concepts more tangible.
- Use differentiated instruction to meet the diverse needs of students and ensure everyone is able to follow along.
- Encourage collaborative learning by having students work in pairs or small groups to solve problems together.
- Provide timely and constructive feedback to guide students through their learning process.
By collaborating effectively and utilizing these strategies, both parents and teachers can help students succeed in their educational journey and develop the skills needed for future success.
Interactive Methods for Learning Math
Engaging students in active learning experiences is one of the most effective ways to deepen their understanding and retain new concepts. By using interactive techniques, learners are more likely to stay motivated and develop problem-solving skills. This section explores various hands-on approaches that can make learning more enjoyable and effective for students, helping them connect theory with practice.
Using Visual Tools and Manipulatives

Visual aids and physical objects can significantly enhance comprehension, especially for young learners. These tools allow students to visualize abstract concepts, making them easier to grasp. Here are some interactive methods that utilize visual tools:
- Number lines: Help students understand the sequence of numbers and perform basic operations.
- Counters and blocks: Allow for hands-on practice with grouping, counting, and simple addition and subtraction.
- Charts and diagrams: Visual representations of problems can make patterns, relationships, and operations clearer.
Gamification and Technology Integration
Incorporating games and technology into learning can make concepts more engaging and foster a competitive yet collaborative learning environment. These methods encourage active participation and provide instant feedback. Some strategies include:
- Educational apps: Interactive apps designed for practicing number operations or solving problems can help reinforce lessons in a fun way.
- Math games: Board games or online challenges that require solving math problems to progress can make learning enjoyable.
- Interactive whiteboards: Use interactive boards to draw, manipulate objects, or work through problems together as a class.
By using these interactive methods, students can develop a deeper understanding of the material, make learning more enjoyable, and build essential skills that will serve them in future academic endeavors.
Strategies to Master Module 4 Content
Mastering the content in any educational segment requires focus, consistent practice, and the right approach. To succeed in understanding and applying the concepts presented, students need to break down the material into manageable steps and employ strategies that reinforce their learning. In this section, we will outline effective methods for mastering the topics covered in this particular unit of study.
Breaking Down Complex Concepts
One of the first steps to mastering new material is to break down complex topics into smaller, more digestible pieces. This approach makes it easier for students to understand and retain information. Some effective techniques for tackling complex concepts include:
- Chunking: Divide larger problems into smaller, simpler parts to avoid overwhelming the learner.
- Step-by-step guides: Create a clear, sequential plan for solving problems, allowing students to follow a structured path.
- Repetition: Practice problems multiple times to reinforce understanding and build confidence.
Hands-on Practice and Active Learning
Active learning methods can significantly enhance comprehension and retention. Engaging directly with the content rather than just reading or listening makes it more likely for students to internalize the material. Some strategies for active learning include:
- Interactive activities: Use games, hands-on exercises, or group work to apply concepts in real-world scenarios.
- Peer teaching: Have students explain the concepts to one another, reinforcing their understanding by teaching.
- Real-life connections: Relate problems to everyday activities, such as shopping or cooking, to show how the concepts are applied outside of the classroom.
Monitoring Progress and Adjusting Techniques
Continuous monitoring is essential to ensure that students are progressing well with the material. Teachers and parents should provide feedback and adjust teaching techniques as necessary. Effective strategies include:
- Frequent quizzes: Use short assessments to gauge understanding and identify areas for improvement.
- Targeted review: Focus on areas where students show difficulty, using extra practice or alternative teaching methods.
- Personalized learning: Adapt instruction based on individual student needs to ensure everyone grasps the concepts at their own pace.
| Strategy | Purpose | Benefit |
|---|---|---|
| Chunking | Breaking down large problems into smaller steps | Reduces overwhelm and improves focus |
| Step-by-step guides | Providing a clear sequence of actions | Clarifies the process and increases success |
| Repetition | Revisiting problems for mastery | Strengthens retention and boosts confidence |
By following these strategies and consistently applying them, students will be well-equipped to master the content and apply it confidently in their studies.
Improving Problem-Solving Skills

Developing strong problem-solving skills is essential for tackling complex challenges in any subject area. These skills enable students to approach unfamiliar problems with confidence, break them down into manageable parts, and apply effective strategies to find solutions. This section focuses on techniques that can help improve students’ ability to solve problems with greater accuracy and efficiency.
Understanding the Problem
The first step in solving any problem is fully understanding what is being asked. Before jumping into calculations or methods, take a moment to analyze the problem. Encourage students to:
- Read carefully: Ensure all parts of the problem are understood before attempting a solution.
- Identify key information: Highlight or underline important numbers, words, or phrases that will guide the solution process.
- Rephrase the problem: Ask students to explain the problem in their own words to ensure they grasp the concept clearly.
Developing a Plan
Once the problem is understood, the next step is to create a plan. Developing a strategy for how to approach the problem ensures a more structured and methodical solution. Some ways to plan effectively include:
- Choosing the right method: Based on the problem, determine the most appropriate strategy–whether it’s drawing a diagram, using counters, or applying known formulas.
- Breaking it down: Divide the problem into smaller, more manageable parts to simplify the solution process.
- Making predictions: Encourage students to think about what the answer might be before starting the calculations, helping them stay focused on the goal.
Practicing Persistence
Not all problems are solved on the first try, and persistence is key to success. Encourage students to stay patient and try different methods if needed. Some ways to build persistence include:
- Trying different strategies: If the first approach doesn’t work, try another method or rethink the steps.
- Working in steps: Focus on solving the problem in stages, rather than feeling overwhelmed by the whole task.
- Reflecting on mistakes: Mistakes are an essential part of the learning process. Encourage students to learn from errors and adjust their approach.
By consistently applying these problem-solving techniques, students will develop the ability to tackle even the most challenging problems with confidence and creativity.
Tips for Students to Excel in Math
Achieving success in any subject requires a combination of hard work, effective strategies, and a positive attitude. For young learners, building a strong foundation and developing a love for problem-solving is essential. Below are some practical tips that can help students excel in their studies, particularly when it comes to handling mathematical concepts and challenges.
1. Practice Regularly
Consistent practice is key to mastering any skill, especially in subjects that involve numbers and calculations. To improve, students should:
- Set aside time each day: Regular practice helps reinforce concepts and enhances recall during tests.
- Work on a variety of problems: Exposure to different types of questions broadens understanding and develops adaptability.
- Review mistakes: Analyzing errors helps students identify areas where they need more practice and learn from their missteps.
2. Understand the Concepts
Understanding the core ideas behind the problems is far more important than simply memorizing formulas or procedures. Students should aim to:
- Ask questions: Whenever something is unclear, students should seek clarification from teachers or peers.
- Break problems into smaller steps: This makes complex problems easier to tackle and ensures no part is overlooked.
- Use visual aids: Diagrams, charts, and manipulatives can help students better understand abstract concepts.
3. Stay Organized
Being organized can make a significant difference in how well students perform. Here’s how staying organized can help:
- Keep notes neat and tidy: Well-organized notes make it easier to review material and locate important information quickly.
- Use a study plan: A schedule that includes time for practice, review, and breaks can help manage time effectively.
- Track progress: Regularly monitoring progress allows students to see how much they’ve learned and what areas still need work.
4. Stay Positive and Motivated
Attitude plays a major role in learning. Students who maintain a positive mindset are more likely to persevere through challenges. Here’s how students can stay motivated:
- Set realistic goals: Small, achievable goals keep students motivated and provide a sense of accomplishment.
- Celebrate progress: Acknowledge achievements along the way to maintain enthusiasm and confidence.
- Stay confident: Encourage a can-do attitude, even when problems seem difficult. Confidence builds over time with practice and persistence.
By applying these tips consistently, students can build a strong foundation and thrive in their studies, not just in solving problems but also in developing the skills necessary for success in future learning.
How Module 4 Builds Math Foundations

The purpose of the fourth unit in early education is to strengthen the core principles that form the basis of future learning. By introducing key concepts and strategies, this unit aims to give students the tools they need to approach more complex topics confidently. Understanding these foundational ideas allows students to build on their knowledge in later years, ensuring they have the skills to succeed in more advanced problem-solving.
One of the main focuses of this section is developing number sense. This is achieved by emphasizing the relationship between numbers and their values. For example, learners explore ways to count, compare, and order numbers, all of which are critical skills for solving problems in different contexts.
Additionally, the section fosters an understanding of basic operations. Simple addition and subtraction, for instance, are taught with an emphasis on mental strategies, helping children grasp the logic behind these operations rather than relying on rote memorization. This method encourages a deeper understanding and encourages students to think critically about numbers.
Key Skills Developed
- Comprehension of number patterns: Students learn how to identify and predict numerical sequences, which enhances their ability to solve complex equations.
- Understanding of place value: Emphasizing how digits within numbers represent different values is crucial for performing larger calculations and setting the stage for learning multiplication and division.
- Introduction to measurement: Students are introduced to the concepts of length, weight, and volume, which form a crucial part of their ability to solve real-world problems.
By focusing on these essential skills, this unit ensures that students are not only prepared for future challenges but also have a solid foundation for applying their knowledge in everyday situations. Understanding these concepts early on enables learners to approach more advanced topics with confidence and a well-rounded skill set.
Practical Applications of Math Concepts
Understanding fundamental concepts is not just about completing exercises in a workbook; it’s about seeing how these ideas work in real life. When students grasp the importance of numbers and operations, they can apply them to solve everyday problems, make informed decisions, and understand the world around them. This section will explore the ways in which these concepts are used in daily activities, providing a deeper understanding of their value.
One of the primary goals of early education is to show how basic skills like counting, measuring, and comparing numbers can be applied in practical settings. For instance, when shopping, children can use addition and subtraction to calculate prices, identify how much change they should receive, or compare the cost of different items. These simple activities build confidence in their ability to solve real-world problems.
Examples of Practical Applications
| Activity | Math Concept | Real-Life Application |
|---|---|---|
| Shopping | Addition and subtraction | Calculating total cost, finding change |
| Cooking | Measurement and fractions | Measuring ingredients for recipes |
| Building projects | Geometry and measurement | Measuring lengths, calculating area or volume |
In addition to these common examples, students can also apply these concepts to tasks like organizing their daily schedules, understanding time, or estimating distances. These hands-on experiences help reinforce the idea that math is not just an abstract subject, but a powerful tool used to navigate life effectively.
Frequently Asked Questions about Module 4

As students progress through their educational journey, it’s common for both parents and teachers to have questions about the content being taught. This section aims to address some of the most frequently asked questions regarding the topics and activities covered in the current level of instruction. Understanding these concepts is crucial for helping students grasp the material and apply it effectively in both academic and everyday contexts.
1. What are the main concepts covered in this section?
This section primarily focuses on developing students’ ability to understand and apply basic number operations, problem-solving strategies, and foundational skills in addition and subtraction. It helps students build the skills needed for more complex topics in future levels.
2. How can I support my child at home with these lessons?
Encourage your child to practice the skills learned in class by using everyday activities like shopping, cooking, or organizing. Simple activities such as counting objects, measuring ingredients, or discussing time can help reinforce the concepts. Additionally, regular practice with simple exercises can strengthen their confidence and understanding.
3. My child is struggling with word problems. What can I do?
Word problems can be challenging, but breaking them down step by step can help. Guide your child by reading the problem together, highlighting key information, and discussing what is being asked. Encourage them to visualize the situation or use manipulatives like blocks or counters to represent the problem. With time and practice, word problems will become easier to handle.
4. Is it necessary to complete every exercise in the workbook?
While completing all exercises is beneficial for reinforcing skills, it’s more important to focus on understanding the concepts. If your child struggles with certain exercises, it’s okay to skip them temporarily and revisit them later after reviewing the material. The goal is comprehension, not just completion.
5. How can I track my child’s progress?
Regularly reviewing completed assignments, quizzes, and practice problems can give you insight into your child’s progress. Many teachers also provide periodic assessments to evaluate their understanding. If needed, reaching out to the teacher for updates or additional support can be helpful for tracking progress and identifying areas for improvement.
Using Worksheets Alongside the Answer Key
Worksheets are an essential tool for reinforcing the concepts taught in the classroom. When used in conjunction with the provided solutions guide, they can be a powerful resource for both students and teachers. By practicing with worksheets and cross-referencing solutions, students can solidify their understanding and identify areas where further clarification is needed. This approach not only builds confidence but also helps in mastering the material more efficiently.
Benefits of Using Worksheets and Solutions Together
Integrating worksheets with the solutions guide offers several advantages:
- Immediate feedback: Students can quickly check their answers against the solutions, identifying mistakes and understanding where they went wrong.
- Self-paced learning: By working through problems at their own speed and reviewing the solutions, students can ensure they fully grasp each concept before moving on.
- Improved problem-solving skills: Worksheets encourage practice and repetition, which are key for mastering problem-solving techniques. With access to solutions, students can see the correct steps and learn from their mistakes.
- Parent and teacher support: Teachers and parents can use the solutions guide to help explain difficult problems and provide additional support when needed.
How to Use Worksheets Effectively
To get the most out of worksheets and solutions, it’s important to follow a structured approach:
- Start with a review: Before tackling the worksheet, review the concepts covered in class to refresh your memory and set the foundation for the work ahead.
- Work through problems independently: Encourage students to attempt the problems on their own first, without immediately referring to the solutions guide. This promotes critical thinking and problem-solving skills.
- Cross-check with the solutions: After completing the worksheet, students can compare their solutions with the guide. If they find discrepancies, it’s an opportunity to revisit the concept and understand the reasoning behind the correct answer.
- Seek help when needed: If a student consistently struggles with certain problems, it may be helpful to go over the steps in detail with the teacher or tutor, referring to the solutions for guidance.
By combining worksheets with the solutions guide, students can enhance their understanding and become more confident in applying the concepts learned in class.
Benefits of Mastering Module 4 Skills
Mastering the skills taught in this unit provides a solid foundation for future learning and enhances overall academic performance. These skills not only improve problem-solving abilities but also foster critical thinking, making students more confident in their abilities to tackle complex challenges. Gaining proficiency in these concepts prepares students for higher levels of learning and helps them apply their knowledge in practical scenarios.
Key Advantages of Mastery
- Strengthened problem-solving abilities: Mastery of the concepts enables students to approach and solve problems with greater confidence and efficiency.
- Improved analytical skills: Understanding the underlying principles boosts students’ ability to break down complex problems into simpler parts and analyze them more effectively.
- Increased self-reliance: Students who fully grasp the concepts become more independent learners, able to apply their knowledge to new and unfamiliar situations without constant support.
- Better performance in future coursework: Mastering the current skills builds a strong academic foundation that will serve students well as they progress in their studies, making it easier to understand more advanced topics.
- Enhanced real-world applications: These skills help students understand how mathematical concepts are used in everyday life, from budgeting and planning to making decisions based on data.
How Mastery Impacts Future Success
- Building confidence: When students feel confident in their understanding of core concepts, they are more likely to approach new challenges with a positive attitude and a willingness to learn.
- Application of learned skills: Students who have mastered the material can apply their skills not just in the classroom, but also in various life situations, such as understanding time, money, and measurements.
- Readiness for more advanced topics: A strong grasp of foundational skills ensures that students are well-prepared for more difficult concepts in the future, allowing them to progress smoothly through their academic journey.
Mastering these skills is an essential step toward academic success and personal growth, providing students with the tools they need to excel both in and outside the classroom.