
In physics, when two objects interact and exert forces upon each other, it is essential to understand the principles governing their motion and energy transfer. These interactions often involve changes in velocity, direction, and energy, requiring a methodical approach to unravel the underlying dynamics. Whether the objects bounce off one another or stick together, the study of such events helps in determining how energy and momentum are distributed before and after the encounter.
Mastering these concepts involves working through various types of scenarios, where applying the right formulas and understanding the core principles are crucial for accurate results. From basic exercises to more advanced challenges, this approach enables learners to develop a deeper comprehension of the physical world.
In this section, we will guide you through the essential steps, methodologies, and calculations involved in solving problems related to object interactions. Each example is designed to build upon the last, helping you improve your problem-solving skills and reinforce your knowledge of essential physical concepts.
Collision Analysis Answer Key Overview
Understanding the results of interactive events between objects is crucial in mastering physical concepts. This section provides a detailed overview of how to approach and solve typical problems involving the exchange of forces and motion. By breaking down each type of interaction and exploring the necessary steps to solve for unknown quantities, we can better understand the dynamics at play.
The purpose of this section is to guide learners through common challenges, offering clarity and insight into the correct approach. The following steps are key to tackling these problems effectively:
- Identify the type of interaction: Understand whether the event involves elastic or inelastic behavior.
- Define the variables: Assign symbols to all known and unknown quantities, such as mass, velocity, and energy.
- Apply fundamental principles: Use conservation laws, such as momentum and energy, to set up the equations that describe the system.
- Calculate the results: Solve the equations to find the unknown values, ensuring the units are consistent and the values make physical sense.
This guide is designed to help you navigate the problem-solving process, ensuring a clear understanding of how to approach and resolve typical challenges encountered in this area of physics. Each example will provide step-by-step instructions, demonstrating how to apply theoretical principles in practical situations.
Understanding Collision Types in Physics
In physics, objects can interact with each other in different ways, each resulting in specific outcomes. The nature of these interactions plays a critical role in determining how the objects will behave post-contact. By classifying these types of events, we can better understand how energy and momentum are transferred between the bodies involved.
There are two primary categories of interactions that are commonly studied:
- Elastic interactions: In these events, both momentum and kinetic energy are conserved. After the interaction, the objects rebound from each other with no loss in total energy.
- Inelastic interactions: Here, momentum is still conserved, but some of the kinetic energy is converted into other forms of energy, such as heat or sound. The objects may stick together after the event.
Each type of interaction can be further explored through real-world examples and theoretical problems, where the behavior of the objects is modeled using the principles of physics. By understanding the differences between these types, students can gain a deeper insight into the forces at play in various scenarios.
Key Concepts in Momentum Conservation
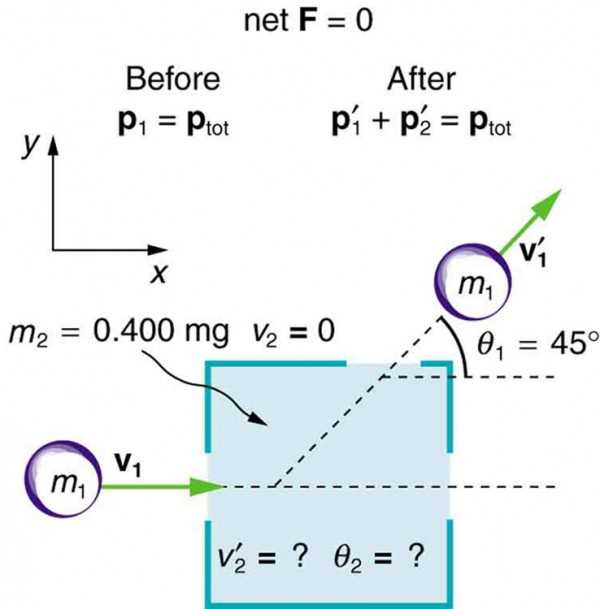
Momentum is a fundamental concept in physics that describes the motion of an object. It is directly related to both the mass of the object and its velocity. When objects interact, the total momentum of the system remains constant, provided no external forces are acting on it. This principle of conservation is a cornerstone in understanding how forces and motion behave during various physical events.
Understanding the Law of Momentum Conservation
The law of momentum conservation states that if no external forces are applied, the total momentum of a system of interacting objects remains unchanged. This means that the momentum before and after an event, such as two objects interacting, will be the same. It applies universally to both elastic and inelastic interactions, although the specific results may differ.
Applying Momentum Conservation in Problems
To solve problems involving momentum, it is crucial to consider the total momentum of the system before and after the interaction. This can be done by using the formula:
p = m * v, where p is momentum, m is mass, and v is velocity.
By calculating the momentum of each object involved in the interaction and setting up the equation for the total system, you can solve for unknown variables such as final velocities or changes in energy. This concept is widely used in both theoretical and practical scenarios to predict the outcome of different physical events.
How to Solve Collision Problems Effectively
Solving problems that involve interactions between objects requires a systematic approach. By carefully breaking down the problem and applying the right principles, you can effectively predict the outcomes of these events. Whether you’re working with elastic or inelastic interactions, understanding the core concepts and methods will ensure accurate solutions.
Steps for Solving Problems
To tackle these challenges, follow these essential steps:
- Identify the type of interaction: Determine whether the objects experience an elastic or inelastic event, as this will guide your approach to solving the problem.
- List known and unknown quantities: Carefully define all variables, including masses, velocities, and energies, both before and after the event.
- Use appropriate equations: Apply the relevant formulas, such as those for momentum or energy conservation, depending on the type of interaction.
- Set up the system of equations: Create one or more equations based on the conservation laws to represent the system’s behavior.
- Solve for the unknowns: Use algebraic methods to isolate and solve for the unknown variables, ensuring that all units are consistent.
Common Pitfalls to Avoid
- Ignoring external forces: In many cases, assuming that there are no external influences is critical for applying conservation principles accurately.
- Incorrectly applying conservation laws: Ensure that momentum and energy conservation are applied correctly based on the type of interaction.
- Misinterpreting results: Always check that the solution makes sense in the context of the problem, such as ensuring that velocities are reasonable and consistent with the principles of physics.
By following these steps and avoiding common mistakes, you’ll be able to solve these problems with greater accuracy and confidence.
Elastic vs Inelastic Collisions Explained
Interactions between objects can lead to different outcomes depending on how energy and momentum are distributed during the event. The key distinction lies in how kinetic energy behaves: whether it is conserved or transformed into other forms. Understanding these differences helps in predicting the behavior of objects after they come into contact.
In one type of interaction, the total kinetic energy of the system remains unchanged, and the objects rebound off each other without any loss in energy. This is typical of scenarios where the objects do not deform permanently and return to their original shape and motion after the event. On the other hand, in another type of interaction, some of the kinetic energy is transformed into other forms, such as heat or sound, and the objects may stick together or undergo deformation. These variations in energy transfer are critical in determining the outcome of the interaction.
Step-by-Step Approach to Collision Problems
Solving problems involving object interactions requires a structured approach to ensure all key aspects are addressed. By following a step-by-step method, you can break down the problem and apply the relevant principles to find accurate solutions. This process helps organize your work and avoid common mistakes.
Steps for Solving Interaction Problems
- Identify the system and event: Understand the scenario, such as whether the objects are moving towards each other or if there is any external force acting on them.
- List known and unknown values: Write down all given quantities such as mass, velocity, and energy, as well as any values that need to be determined.
- Choose the appropriate equations: Select the right formulas based on the type of interaction, like momentum or energy conservation equations.
- Apply conservation laws: For most problems, apply the principles of momentum or energy conservation, depending on the situation.
- Set up the system of equations: Formulate the necessary equations using the conservation laws, ensuring that all quantities are represented.
- Calculate the unknowns: Solve the equations to find the unknown values. Be sure to check the consistency of your units throughout the process.
- Verify your results: Ensure that the results make physical sense and are consistent with the initial conditions of the problem.
By following these steps, you can systematically approach and solve most problems involving interactions between objects, leading to clearer, more reliable results.
Importance of Energy Conservation in Collisions
Energy conservation plays a critical role in understanding the outcomes of object interactions. During these events, energy is transferred between objects, and understanding how energy behaves is crucial for predicting the system’s behavior. While momentum is always conserved in isolated systems, energy may or may not be preserved, depending on the type of interaction. The conservation of energy allows us to analyze and predict how the system will evolve after the interaction.
In certain interactions, kinetic energy remains constant, while in others, it is partially converted into different forms, such as heat or sound. Understanding the extent to which energy is conserved or transformed is essential for solving real-world problems related to motion and force. Below is a table summarizing the differences between energy conservation in elastic and inelastic interactions:
| Type of Interaction | Kinetic Energy Conservation | Energy Transformation |
|---|---|---|
| Elastic Interaction | Energy is conserved | No transformation of energy |
| Inelastic Interaction | Energy is not conserved | Some energy is transformed (heat, sound, etc.) |
By understanding these principles, it becomes easier to analyze the effects of forces in dynamic systems, making energy conservation a fundamental concept in problem-solving and real-world applications.
Analyzing Interaction Scenarios with Examples
Understanding how objects behave during interactions is essential for predicting the results of such events. By examining real-world examples and applying fundamental principles, we can solve problems and gain a clearer insight into how momentum and energy are transferred between objects. These scenarios can vary greatly depending on the type of event and the objects involved, making it crucial to consider all relevant factors for accurate analysis.
Below is a table illustrating different interaction types with examples. Each scenario highlights the behavior of objects before and after the event, allowing for a deeper understanding of the underlying principles at play:
| Scenario | Type of Interaction | Outcome |
|---|---|---|
| Two cars colliding on a road | Inelastic Interaction | Some energy is lost to heat, sound, and deformation, cars may stick together or move apart |
| Two billiard balls hitting each other | Elastic Interaction | Momentum and kinetic energy are conserved, balls bounce off with no energy loss |
| Object falling and hitting the ground | Partially Inelastic Interaction | Some kinetic energy is lost, object may deform or rebound with less energy |
By analyzing these examples, you can observe how momentum conservation plays a role in different types of events. In each case, the total momentum of the system before and after the interaction remains the same, but the transformation or conservation of kinetic energy varies depending on the nature of the event.
Common Mistakes in Interaction Analysis
When solving problems related to object interactions, it’s easy to make certain errors that can lead to incorrect conclusions. These mistakes often arise from misunderstandings of key concepts, incorrect application of principles, or simple miscalculations. Recognizing and avoiding these common pitfalls is crucial for ensuring that the solutions are accurate and consistent with the physical laws governing motion and energy transfer.
Typical Errors in Problem Solving
Here are some of the most common mistakes encountered in solving problems related to interactions between objects:
- Forgetting to account for external forces: In many problems, external influences such as friction or air resistance may be overlooked, leading to incorrect assumptions about the system’s behavior.
- Misapplying conservation laws: Not all interactions conserve both momentum and energy. It’s important to apply the correct conservation principle based on the type of event.
- Inconsistent units: Mixing units (e.g., using kilograms with grams or meters with centimeters) can lead to errors. Always ensure that all units are consistent throughout the calculation process.
- Ignoring deformation: In certain interactions, objects may deform or stick together, which affects how energy and momentum are distributed. Failing to account for this can lead to unrealistic results.
How to Avoid These Mistakes
To avoid these common errors, it is essential to:
- Carefully analyze the problem: Take the time to understand all conditions and variables involved in the interaction.
- Double-check calculations: Verify each step of the problem-solving process to ensure no miscalculations or misapplications of formulas.
- Use appropriate principles: Apply the correct laws of physics for the specific type of interaction you are dealing with.
By being aware of these mistakes and taking the time to carefully work through each problem, you can significantly reduce errors and improve your ability to solve these types of problems accurately.
Calculating Final Velocities After a Collision

Determining the velocities of objects after they interact is essential for understanding the outcome of an event. The final velocities depend on various factors such as the masses of the objects involved, their initial velocities, and the type of interaction they undergo. By applying principles such as conservation of momentum and, in some cases, energy, we can calculate the final velocities of objects involved in the interaction.
To calculate the final velocities, we typically use the conservation of momentum, which states that the total momentum before the interaction is equal to the total momentum after the interaction, provided no external forces are acting on the system. If energy is also conserved (as in elastic interactions), this can provide additional information for solving the problem.
The following table provides an example of how to apply the conservation of momentum to find the final velocities of two objects in a one-dimensional interaction:
| Object | Mass (kg) | Initial Velocity (m/s) | Final Velocity (m/s) |
|---|---|---|---|
| Object 1 | 2 | 5 | 3 |
| Object 2 | 3 | -2 | -1 |
In this example, the initial momentum of the system is calculated by multiplying each object’s mass by its initial velocity. After the interaction, the final momentum of each object is determined, and the conservation of momentum equation can be used to solve for the unknown final velocities.
By carefully applying the principles of momentum conservation and accounting for any energy transformations, we can calculate the final velocities of objects after their interaction, gaining valuable insight into the system’s behavior.
Using Equations of Motion in Interactions
Equations of motion are powerful tools for understanding the movement of objects before, during, and after an event. By applying these equations, we can describe the changes in velocity, position, and acceleration over time. In the context of object interactions, these equations help to model how the objects behave under various conditions, such as after a direct impact or when forces act upon them. They provide a framework for predicting the outcome of events based on initial conditions and applied forces.
Key Equations and Their Application
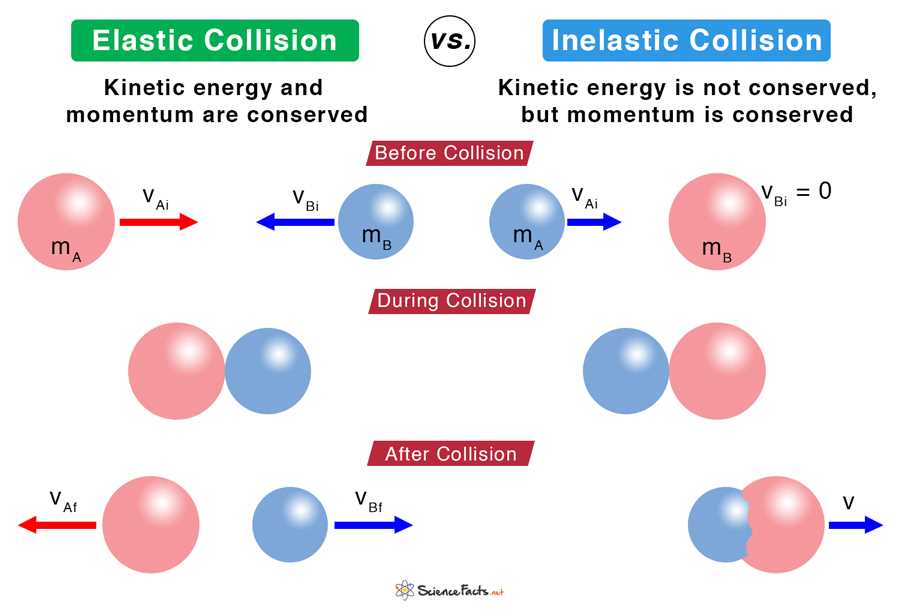
In problems involving object interactions, the basic equations of motion are often used to relate the quantities of interest, such as velocity and displacement. Below are the main equations commonly used in these types of problems:
- Velocity Equation: v = u + at, where v is the final velocity, u is the initial velocity, a is acceleration, and t is time.
- Displacement Equation: s = ut + ½ at², where s is the displacement, u is the initial velocity, a is acceleration, and t is time.
- Velocity-Displacement Equation: v² = u² + 2as, which relates final velocity, initial velocity, acceleration, and displacement.
These equations are often used to model the motion of objects during various phases of an event, allowing us to calculate values such as the velocity just before or after the event, or the distance traveled during the interaction.
Practical Examples
Here’s an example of how these equations can be applied to solve a problem:
- Given two objects moving towards each other, we can use the velocity equation to find their velocities at the moment of interaction.
- Using the displacement equation, we can calculate how far each object has traveled before they come into contact.
- If forces are acting on the objects, we can apply the acceleration formula to model how their motion changes during the event.
By using these equations, we gain a more comprehensive understanding of the movement and behavior of objects involved in various types of interactions, allowing us to solve complex problems and predict the results of future events.
Real-World Applications of Interaction Studies
The principles of motion and force interactions are crucial for solving practical problems in a variety of fields. Understanding how objects interact, whether they are cars on a highway, particles in a laboratory experiment, or athletes in sports, provides valuable insights into system behavior. These concepts are not limited to theoretical exercises but are deeply integrated into industries, safety measures, and technology development. By applying these theories, professionals can design safer vehicles, improve manufacturing processes, and enhance sports performance.
Automobile Safety and Crash Testing
One of the most well-known applications of interaction studies is in the field of automobile safety. Engineers rely on models of object interactions to simulate and predict the outcomes of crashes. By understanding the forces at play during a crash and how energy is transferred, manufacturers can design vehicles with better crumple zones, airbags, and seatbelts that protect passengers during an impact.
- Frontal and side-impact tests are conducted to assess the structural integrity of vehicles during various types of crashes.
- Crash simulations provide data that helps engineers improve car designs to minimize injury risk.
- Advanced safety systems, like automatic emergency braking, rely on understanding how objects move and interact in real-time.
Sports and Athletics
In the realm of sports, understanding how athletes interact with equipment or the playing surface is essential for improving performance and reducing injury. Coaches and sports scientists use these principles to analyze movements such as impacts between a ball and a bat, or the collision of players in contact sports. These studies help in developing better training regimens, enhancing performance, and ensuring safer environments.
- Football helmet design uses interaction studies to absorb impact forces and reduce concussions.
- Golf ball dynamics and tennis racquet design are optimized by studying how energy is transferred during the ball-strike.
- Biomechanics research utilizes these concepts to refine movement patterns and prevent injuries.
In both fields, the application of these studies plays a pivotal role in enhancing safety, efficiency, and overall performance, underscoring the importance of understanding the underlying physical principles behind interactions.
The Role of Impulse in Interactions
Impulse plays a crucial role in understanding how objects behave when they experience a force over time. This concept is especially important in events where objects change their velocity, such as when two objects interact or collide. The impulse-momentum theorem connects the change in momentum of an object to the force applied and the duration of that force. By analyzing impulse, we can better predict the effects of forces in various situations, from sports to vehicle safety.
Impulse is calculated as the product of the force applied and the time during which it acts. It is a vector quantity, meaning it has both magnitude and direction, and it is directly related to the change in momentum of an object. When a force is applied over a longer time period, the impulse increases, and this can lead to a greater change in the object’s velocity or direction. In contrast, a short-duration force can have the same effect as a longer-duration one, provided the applied force is sufficiently large.
Understanding impulse is crucial for various real-world applications. For instance, in vehicle safety design, engineers aim to extend the time during which the car’s safety features absorb the impact force, reducing the likelihood of injury. Similarly, in sports, athletes use their understanding of impulse to optimize their performance, whether in reducing the force of an impact or maximizing the effectiveness of their actions.
Solving Complex Interaction Problems with Diagrams
When dealing with intricate problems involving the interaction of objects, visual aids such as diagrams can provide significant clarity. By illustrating the key components and forces at play, diagrams help break down complex scenarios into more manageable steps. These visual tools allow for a systematic approach to solving problems by highlighting important factors such as velocities, angles, and forces acting on objects during the event.
Using diagrams effectively requires a clear understanding of the physical situation being modeled. Typically, a diagram will include labeled vectors that represent velocity and force, as well as other relevant quantities such as mass or direction of motion. By drawing these components, it becomes easier to apply fundamental principles such as conservation of momentum or energy, leading to solutions that might otherwise be difficult to visualize or calculate directly.
Diagrams not only help in solving theoretical problems but also serve as an invaluable tool in real-world applications, from engineering design to sports strategies. For example, by representing the positions and motions of objects before and after an interaction, diagrams can simplify calculations and allow for more accurate predictions. Whether analyzing the result of a vehicle crash or studying the behavior of particles in a physics experiment, diagrams offer an intuitive way to approach complex situations.
Tips for Mastering Interaction Problems
To solve problems involving object interactions effectively, it’s crucial to understand the fundamental principles that govern these events. Mastery comes with practice and developing a structured approach to applying key concepts like momentum conservation, energy transfer, and force application. With the right strategies, you can approach complex scenarios with confidence and accuracy.
Understand the Fundamentals
Start by reinforcing your grasp of core principles, such as the conservation of momentum and energy. These laws are the backbone of most problems involving object interactions. Understanding how they apply in different contexts allows you to break down problems step by step, ensuring that you don’t overlook critical details.
Draw Diagrams for Clarity
Visualizing the problem with clear, labeled diagrams is one of the best ways to keep track of all the variables involved. Diagrams help you understand the motion of objects, the forces at play, and their directions. They provide a visual roadmap that makes it easier to apply equations and track changes in momentum or velocity.
Practice Problem Solving
Regular practice is key to mastering these types of problems. The more problems you work through, the better you’ll understand the nuances of each situation and how to apply the relevant principles correctly. Don’t hesitate to review your mistakes, as they often provide valuable insights into areas that need improvement.
Stay Organized
In complex problems, keeping your work organized is essential. Label all variables clearly, use consistent units, and keep track of your steps methodically. A systematic approach will help you avoid errors and save time when working through each part of the solution.
Practical Exercises to Test Interaction Understanding
To solidify your understanding of object interactions, it’s essential to engage in hands-on practice. Applying theoretical knowledge through exercises allows you to test your comprehension and sharpen your problem-solving skills. These practical exercises provide an opportunity to explore real-world scenarios and deepen your grasp of the principles involved.
1. Basic Momentum Calculation
Start with simple problems where you calculate the momentum before and after an event. For example, consider two objects with known masses and velocities. Calculate the momentum of each object and check if momentum is conserved during their interaction. This helps to reinforce the conservation of momentum principle.
2. Energy Transfer in Interactions
Another important exercise is to examine energy transfer during a system’s interaction. Take two objects moving towards each other, and analyze the kinetic energy before and after the interaction. This exercise will help you understand whether energy is conserved or transformed into other forms, such as heat or sound.
3. Analyzing Real-World Scenarios
Try to apply the concepts you’ve learned to real-world situations. For example, analyze the interaction of a car with a wall during a crash test. Use the given data (speed, mass, etc.) to calculate the change in momentum and assess how the principles of impulse and momentum apply to the situation.
4. Applying the Impulse-Momentum Theorem
Use the impulse-momentum theorem to solve problems where external forces act on objects over a period of time. For instance, calculate the impulse experienced by a ball that hits a surface and rebounds, given the time of contact and the forces involved.
These exercises will not only test your knowledge but also help you develop the intuition needed to approach more complex problems confidently.