
In this guide, we will explore a vital part of your learning journey focused on critical concepts and techniques that are fundamental to solving mathematical challenges. Whether you’re revisiting familiar topics or encountering new ones, the goal is to build a deeper understanding that will help you approach each problem with confidence.
Effective problem-solving requires a combination of clear strategies, practice, and careful review. By breaking down complex exercises into manageable steps, you’ll enhance your ability to tackle even the most challenging tasks. Throughout this section, you’ll be guided through various methods that simplify intricate concepts and provide clear paths to solutions.
As you progress, this material will serve as a reliable resource for checking your work and understanding how to approach different types of questions. You’ll gain insights into how to structure your thinking and improve your skills, ensuring that you are fully prepared for more advanced problems ahead.
Algebra Nation Section 3 Answer Key
In this part of the material, we focus on providing clear solutions and explanations for the exercises you’ve encountered. By thoroughly reviewing the steps involved in each problem, you’ll gain a deeper understanding of the methods and reasoning behind each approach.
Working through these detailed solutions helps reinforce your learning and ensures that you fully comprehend the steps needed to solve each problem. The goal is not just to find the correct result but to develop a systematic process that you can apply to other challenges in the future.
By utilizing these solutions, you’ll be able to check your progress and identify areas that need further practice. With careful analysis of the methods used, you’ll refine your problem-solving skills and build greater confidence as you move forward.
Understanding Key Concepts in Section 3
This portion of the material delves into the essential ideas and principles that are central to solving the exercises presented. It’s crucial to grasp these foundational concepts as they form the basis for successfully tackling more complex problems later on.
Each concept builds on the last, creating a logical progression that enhances your ability to think critically and solve challenges effectively. By mastering these core principles, you’ll be better equipped to handle a variety of related tasks and deepen your overall understanding of the subject.
Focusing on these critical elements will help you develop a structured approach to problem-solving, making it easier to break down difficult problems into manageable parts. The goal is to ensure that you are not just memorizing methods, but also understanding the reasoning behind them to apply the techniques with confidence in different contexts.
Step-by-Step Problem Solving Techniques
Mastering a systematic approach to solving problems is key to overcoming even the most complex challenges. By breaking down each problem into smaller, manageable steps, you can develop a clear path to the solution while ensuring accuracy along the way.
Breaking Down the Process
The first step in tackling any problem is to understand the task at hand. Start by identifying what is being asked and the known information. From there, follow a logical progression to find the solution.
- Read the problem carefully to ensure full comprehension.
- Highlight the key information and variables.
- Identify the steps needed to reach a solution.
- Break the problem into smaller, solvable parts.
- Check your work at each step for accuracy.
Using Visualization and Tools
In some cases, visualizing the problem can help clarify the steps and relationships between variables. This could include drawing diagrams, using tables, or even creating graphs to better understand the situation.
- Sketch out diagrams or graphs to represent the problem visually.
- Use tables to organize information logically.
- Work with different tools such as calculators or software when applicable.
By following a structured, step-by-step approach and utilizing visual aids when necessary, you can approach any problem with greater clarity and confidence, ensuring a more efficient and accurate solution process.
Common Mistakes to Avoid in Algebra
When solving mathematical problems, it’s easy to make small errors that can lead to incorrect results. These mistakes often arise from misunderstandings of key concepts or from rushing through steps without checking the work. Recognizing and addressing these pitfalls can help you improve your accuracy and efficiency in solving problems.
Misinterpreting Problem Requirements
A frequent mistake is failing to fully understand the problem before attempting to solve it. It’s important to carefully read through all the details and identify exactly what is being asked.
- Skipping important information or assumptions.
- Not recognizing the correct operations required.
- Overlooking units or variable relationships in word problems.
Errors in Basic Operations
Even with a solid understanding of the concepts, performing basic operations incorrectly can lead to mistakes. Double-checking simple calculations can save a lot of time and frustration later.
- Incorrectly applying rules of arithmetic operations.
- Forgetting to apply parentheses or the order of operations.
- Misplacing decimal points or signs during calculation.
By being mindful of these common mistakes and taking the time to review each step carefully, you can avoid unnecessary errors and enhance your problem-solving skills.
How to Use the Answer Key Effectively

Accessing the solution guide is an essential tool in refining your problem-solving skills. However, it’s important to use it strategically, rather than simply copying the results. By understanding the reasoning behind each solution, you can improve your comprehension and ability to tackle similar problems on your own.
Review the Process, Not Just the Result
It’s easy to glance at the final answer and assume you’ve mastered the problem, but the real learning happens when you analyze the steps that led to the solution. Focus on understanding each stage and how it contributes to the overall outcome.
- Compare your approach with the guide’s steps.
- Identify any differences in method and correct them.
- Take note of any shortcuts or strategies you may have missed.
Use It for Self-Assessment

Instead of relying on the guide for every question, try solving the problem yourself first, then check your work. This method encourages critical thinking and helps you spot errors while reinforcing the correct process.
- Attempt the problem on your own before verifying your answer.
- Use the solution to identify mistakes and understand why they occurred.
- Review the reasoning behind each decision to strengthen your grasp of the material.
By treating the solution guide as a learning tool rather than a shortcut, you’ll gain a deeper understanding of the subject and improve your problem-solving abilities.
Exploring Practice Problems for Mastery
Consistent practice is essential for mastering any mathematical concept. By working through a variety of exercises, you not only reinforce what you’ve learned but also identify areas where you need further improvement. Tackling diverse problems strengthens your problem-solving abilities and prepares you for more advanced topics.
The Importance of Variety in Practice
It’s crucial to expose yourself to different types of problems, as each one helps develop a unique skill set. While some problems may seem simple, they often require you to apply concepts in different ways, testing your understanding and adaptability.
- Start with basic problems to build confidence.
- Gradually increase difficulty to challenge your skills.
- Work on problems that require creative solutions or multiple steps.
Building Confidence Through Repetition
Repetition is one of the most effective ways to gain mastery. By revisiting problems multiple times, you internalize the methods and patterns that lead to correct solutions, making future tasks easier to tackle.
- Reattempt problems that you initially struggled with.
- Focus on areas where you’ve made mistakes to ensure full comprehension.
- Track your progress over time to monitor improvement.
By approaching each problem with a focused mindset and a determination to learn from each attempt, you’ll achieve a high level of mastery that will benefit you in more complex exercises.
How Section 3 Connects to Previous Sections

Understanding how each topic builds upon the previous one is crucial for mastering the material. The concepts introduced in this part are not isolated; they rely heavily on the foundational knowledge gained in earlier chapters. This progression allows for a smoother transition into more advanced material and helps you see the relationships between different ideas.
Linking New Ideas with Earlier Concepts
As you dive deeper into the content, you’ll notice that many of the techniques covered in this section are extensions of what you’ve already learned. By revisiting earlier concepts, you strengthen your grasp on them and expand your problem-solving toolkit.
- Reinforce the basics to better understand complex topics.
- Recognize recurring methods that have been introduced in earlier parts.
- Apply previous lessons to simplify new problems.
Building on Prior Knowledge

Each new concept in this section is designed to be a natural progression from the material you’ve already studied. This allows you to apply what you know while introducing more advanced techniques and approaches that require a solid understanding of earlier principles.
- Identify how earlier lessons support new material.
- See how different methods connect to solve more complex challenges.
- Leverage previous knowledge to master new strategies and skills.
By recognizing the connections between topics, you’ll develop a more cohesive understanding of the material, making it easier to apply concepts across different types of problems.
Tips for Speeding Up Problem Solving
Improving the speed at which you solve problems is an essential skill, especially when dealing with time-sensitive exercises. By adopting efficient strategies and streamlining your approach, you can tackle problems faster without sacrificing accuracy. The key lies in preparation, practice, and optimizing your problem-solving process.
Master the Basics
One of the most effective ways to speed up solving tasks is by mastering the core principles and methods. When you have a strong foundation, you can recognize patterns and solutions quickly, eliminating the need for repetitive calculations or unnecessary steps.
- Familiarize yourself with common problem types and solutions.
- Memorize key formulas and techniques for quicker recall.
- Practice core operations to increase fluency and reduce hesitation.
Work Efficiently with Steps
Instead of overthinking each part of a problem, break it down into clear, logical steps. Stay focused on the process, and avoid unnecessary detours. With each step, ask yourself if it brings you closer to the solution, and streamline where possible.
- Prioritize the most effective methods to solve the problem.
- Minimize redundant calculations by simplifying expressions early on.
- Work on improving mental math skills to speed up basic operations.
By implementing these techniques and practicing regularly, you’ll develop greater speed and efficiency in solving problems, allowing you to tackle challenges more confidently and quickly.
Improving Algebra Skills with Section 3
Strengthening mathematical skills requires consistent practice and a focused approach to learning new techniques. The material covered in this part is designed to enhance your understanding of key principles and help you build on previous knowledge. By mastering the concepts presented here, you will improve your problem-solving abilities and gain confidence in tackling more complex challenges.
Applying New Methods to Everyday Problems
This section introduces practical methods that can be applied to a wide range of problems. By practicing these techniques regularly, you can improve your ability to solve real-world scenarios more efficiently.
- Focus on understanding the logic behind each method.
- Apply new strategies to a variety of exercises to reinforce learning.
- Work on recognizing when to use specific techniques based on problem structure.
Building Confidence through Practice
The more you practice the concepts covered, the more confident you will become in your abilities. Regular exposure to these problems helps reinforce concepts and reduces the likelihood of making errors when faced with more difficult tasks.
- Challenge yourself with progressively harder problems to test your understanding.
- Track your progress and celebrate improvements to stay motivated.
- Don’t be afraid to revisit problems to refine your problem-solving process.
By continuing to apply the methods and strategies from this part, you will gradually strengthen your skills, making it easier to approach more advanced material in the future.
Breaking Down Complex Problems in Algebra
When faced with challenging tasks, the best approach is to break them down into smaller, more manageable parts. Complex problems often seem overwhelming at first, but by isolating each component and tackling them individually, you can simplify even the most intricate exercises. This method not only makes solving the problem easier but also boosts your confidence in handling difficult material.
Identifying the Key Elements
The first step in solving a difficult problem is to identify the essential components. Recognizing what the problem is asking for and pinpointing the known values can help you avoid unnecessary steps and focus on the critical elements needed to reach a solution.
- Highlight the variables and constants that are given.
- Understand the goal of the problem–what needs to be found or solved for.
- Identify any patterns or relationships between different elements of the problem.
Breaking Down the Process
Once you’ve identified the key elements, divide the problem into smaller steps. Focus on solving each part sequentially, ensuring that you fully understand each stage before moving on to the next. This method allows you to build momentum and reduces the likelihood of errors.
- Start with the easiest part of the problem and work your way up.
- Use intermediate steps to simplify complicated calculations or concepts.
- Reassess your approach if you find that one step is too difficult or complex.
By breaking down complex challenges into manageable pieces, you will find that solving difficult tasks becomes a much more straightforward process. With each smaller solution, you move closer to the final answer, improving your problem-solving skills along the way.
Key Strategies for Section 3 Success
Achieving success in challenging exercises requires more than just understanding the content–it demands an approach that emphasizes preparation, practice, and effective problem-solving methods. The following strategies can guide you to master the material, boost your efficiency, and enhance your overall performance. By following these steps, you will be well-equipped to tackle the most difficult tasks with confidence.
Organizing Your Approach
One of the most crucial strategies for success is organizing your approach before diving into a problem. Breaking down complex problems into smaller, manageable tasks can make a significant difference in how efficiently you work through them.
| Strategy | Benefit |
|---|---|
| Read the Problem Carefully | Ensure full understanding of what is being asked and identify key information. |
| Break the Problem into Steps | Reduce complexity by focusing on one part at a time. |
| Focus on Concepts | Deep understanding of core principles leads to faster and more accurate solutions. |
Regular Practice and Review
Consistent practice is essential for reinforcing concepts and improving your problem-solving speed. Set aside dedicated time for review to ensure that you retain what you’ve learned and can apply it when needed.
| Action | Purpose |
|---|---|
| Practice Regularly | Repetition builds familiarity with problem types and strengthens recall. |
| Review Mistakes | Learn from errors to avoid repeating them and enhance problem-solving skills. |
| Work on Timed Practice | Improve speed and accuracy by practicing under time constraints. |
By applying these key strategies consistently, you will enhance your ability to approach and solve problems efficiently, helping you to succeed in this area and beyond. Mastering these techniques will enable you to approach complex tasks with greater ease and effectiveness.
Analyzing Common Errors in Algebra Exercises
When working through mathematical tasks, many students encounter similar mistakes that hinder their progress. Recognizing and understanding these common errors is essential for improving accuracy and efficiency. By identifying the frequent pitfalls, you can develop strategies to avoid them and enhance your problem-solving skills.
Identifying Frequent Mistakes
The first step in correcting errors is understanding what causes them. Often, mistakes stem from misinterpreting the question, skipping critical steps, or misunderstanding fundamental concepts. Identifying these errors allows you to address the root causes and prevent them in the future.
| Error Type | Possible Cause | Solution |
|---|---|---|
| Misreading the Problem | Rushing through the problem or not fully understanding the question | Read each question carefully and highlight key information |
| Sign Errors | Forgetting to account for negative signs or incorrect handling of them | Check each sign carefully and double-check calculations |
| Skipping Steps | Attempting to solve problems too quickly without proper steps | Follow a step-by-step approach and avoid shortcuts |
Addressing Conceptual Gaps

Many errors stem from a lack of understanding of the underlying principles. It’s important to recognize when a mistake is the result of a gap in knowledge. In such cases, it’s beneficial to revisit the basic concepts and practice them until you feel more confident.
| Conceptual Mistake | Cause | Fix |
|---|---|---|
| Poor Understanding of Variables | Confusion over the role of variables in equations | Review basic rules of variables and practice substitution |
| Incorrect Application of Operations | Misapplying operations such as multiplication or division | Review operation order (PEMDAS) and practice simple problems |
| Not Recognizing Patterns | Failure to spot recurring structures or relationships | Work on identifying and understanding common mathematical patterns |
By understanding the causes of common errors, you can take proactive steps to avoid them, ensuring greater accuracy in your solutions. Identifying and correcting mistakes will help reinforce your understanding and improve your overall performance.
Mastering Algebraic Equations from Section 3
To truly master mathematical problems, it’s essential to develop a strong foundation in solving algebraic equations. These types of problems require a clear understanding of variable manipulation, balancing both sides of an equation, and applying the right operations to isolate the unknowns. By focusing on these core principles, you can confidently solve even the most complex expressions and enhance your overall problem-solving abilities.
Approaching Linear Equations
Linear equations, where the highest power of the variable is one, form the basis of many algebraic tasks. These are often the first type of problems students encounter and mastering them provides a solid foundation for more advanced topics. The key to solving linear equations is to isolate the variable by performing inverse operations on both sides of the equation.
- Start by simplifying both sides of the equation if possible.
- Use inverse operations (addition, subtraction, multiplication, division) to isolate the variable.
- Double-check your work by substituting the solution back into the original equation.
Solving Quadratic Equations
Quadratic equations, where the highest power of the variable is two, require a slightly different approach. These problems can be solved using methods such as factoring, completing the square, or applying the quadratic formula. A strong understanding of these methods is essential for tackling a wide variety of mathematical challenges.
- Factor the quadratic expression if possible.
- If factoring is not straightforward, apply the quadratic formula: x = (-b ± √(b²-4ac)) / 2a.
- Check for extraneous solutions and ensure the solution makes sense within the context of the problem.
Mastering these techniques will significantly improve your ability to tackle algebraic equations in any context. With consistent practice and attention to detail, solving these types of problems will become second nature.
Reviewing the Answer Key for Accuracy
After completing a set of exercises, it is crucial to review the provided solutions to ensure their accuracy. This step allows you to verify your own work, identify any mistakes, and understand the correct process to reach the solution. A thorough review can also highlight patterns in the types of mistakes commonly made, providing opportunities for improvement.
Steps to Verify the Correctness of Solutions
To accurately check your solutions, follow these simple steps:
- Compare each solution with the provided answers carefully, making sure every step aligns correctly with the expected result.
- Double-check your calculations to ensure no errors in arithmetic or logic were made.
- If the solution process involves multiple steps, break down each step and confirm its validity before moving on to the next one.
- If possible, solve the problem a second time using a different method to verify the result.
Common Mistakes to Watch For
During the review process, pay special attention to the following frequent errors:
- Incorrectly applying mathematical operations or order of operations.
- Sign errors when dealing with negative numbers or fractions.
- Omitting steps or skipping over necessary calculations.
- Forgetting to check if the solution makes sense within the context of the problem.
By carefully reviewing the solutions and identifying any discrepancies, you can build a deeper understanding of the problem-solving process and improve your overall accuracy in future exercises.
Using Section 3 to Prepare for Exams
Effective exam preparation often relies on focused practice and a thorough understanding of core concepts. By revisiting exercises from earlier topics, you can reinforce your knowledge and improve problem-solving skills. Section 3 offers an opportunity to delve deeper into specific areas that are likely to be tested, helping you identify strengths and weaknesses before exam day.
To make the most of your review sessions, concentrate on understanding the underlying principles of the problems. Instead of simply memorizing solutions, focus on the methods and strategies that lead to correct answers. This approach will not only enhance your problem-solving speed but also build a stronger foundation for tackling more complex questions in the future.
Regularly practicing with problems from this part of your study material allows you to build confidence and assess your readiness. The more familiar you become with the types of questions and techniques used, the better equipped you will be to handle similar challenges under exam conditions.
How to Approach Word Problems in Algebra
Word problems can often seem daunting, but breaking them down into smaller, manageable steps can make them much easier to tackle. The key to solving these types of questions is understanding the problem, identifying what is being asked, and translating the given information into mathematical expressions. With practice, this process can become second nature and significantly improve your problem-solving skills.
Step-by-Step Approach
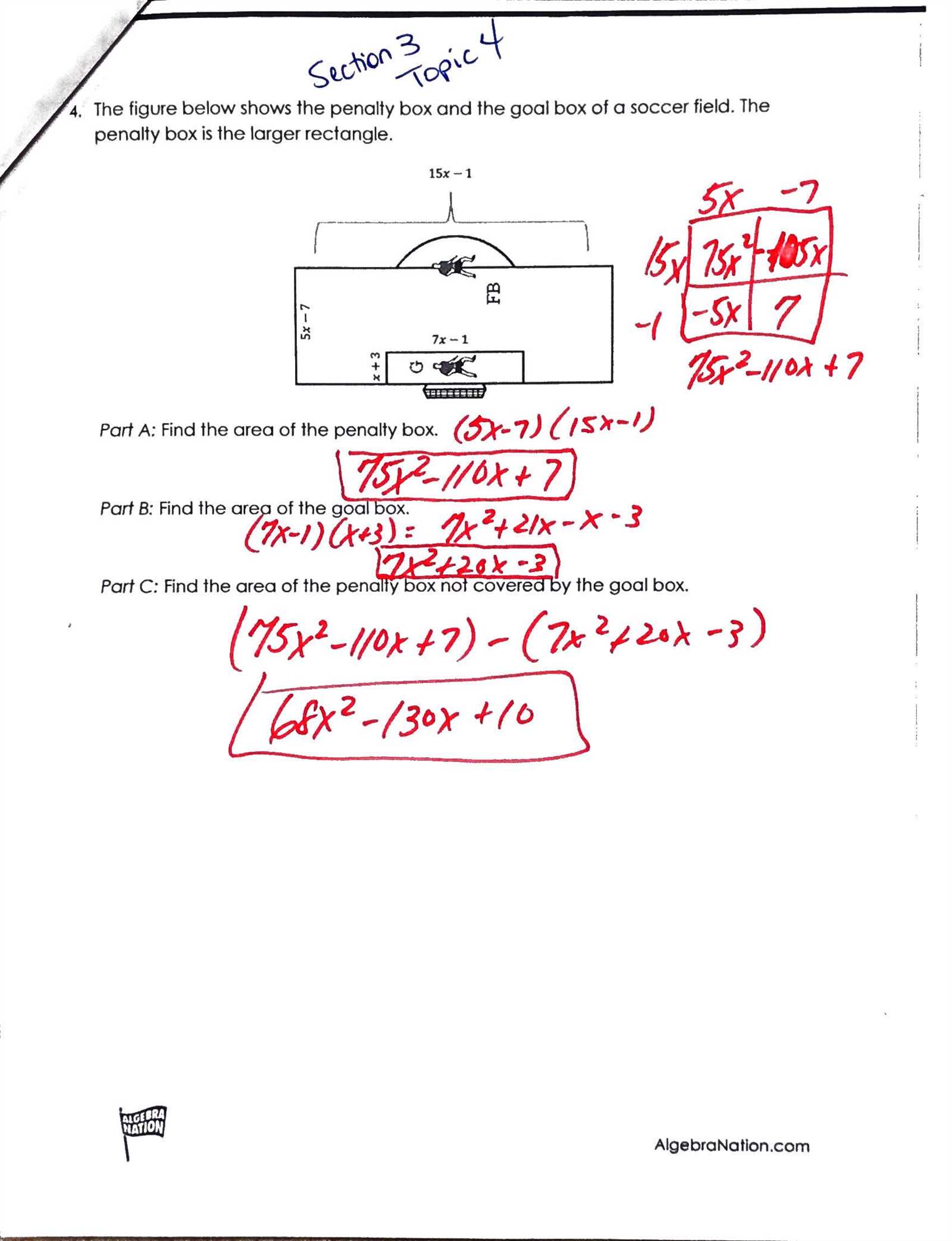
When faced with a word problem, follow these steps to approach it logically:
- Read the problem carefully: Understand the context and what is being asked before jumping into calculations.
- Identify known and unknown variables: Highlight key pieces of information that can be translated into variables or equations.
- Translate the words into equations: Use the clues provided in the problem to create an equation or set of equations that represent the situation.
- Solve the equation: Apply the appropriate mathematical methods to solve for the unknowns.
- Check your work: Once you’ve solved the equation, go back and verify that the solution makes sense in the context of the problem.
Common Tips for Success
- Break down complex problems: If the problem is long or complicated, try breaking it into smaller, simpler parts that are easier to solve.
- Draw diagrams or use tables: Visual aids can help clarify relationships between variables and make it easier to organize information.
- Look for key words: Certain words in the problem, such as “sum,” “difference,” “product,” and “quotient,” can indicate which operations to use.
By following these steps and practicing regularly, you can improve your ability to solve word problems efficiently and accurately.
Building Confidence with Section 3 Challenges

Successfully tackling difficult exercises and problems is one of the best ways to boost your confidence in any subject. The challenges presented in this particular portion offer opportunities to push your limits and strengthen your skills. As you work through these tasks, it’s important to stay persistent and recognize progress, even with the smallest steps.
With each problem solved, you not only reinforce your understanding of key concepts but also build the resilience needed to face increasingly difficult questions. This process fosters a sense of achievement and helps eliminate any self-doubt, ultimately improving both performance and confidence.
Tips for Overcoming Challenges
- Start with a clear plan: Before diving into the problem, take a moment to analyze what’s being asked. Identify knowns, unknowns, and decide the best approach to solving the problem.
- Break it down: If a problem feels overwhelming, divide it into smaller, more manageable parts. This helps you focus on one step at a time and reduces the sense of complexity.
- Use trial and error: Don’t be afraid to try different approaches. Experimenting with multiple strategies can often lead to discovering the best method to solve the problem.
- Learn from mistakes: Every error is an opportunity to learn. Carefully review any incorrect solutions to understand what went wrong and how you can avoid the same mistake in the future.
Building a Growth Mindset

Building confidence is not just about getting the right answers; it’s also about developing a positive attitude towards learning. Embrace mistakes as part of the learning process, and focus on continual improvement rather than perfection. Celebrate your progress and approach each challenge with a mindset geared towards growth.
By consistently engaging with these challenges and adopting a resilient mindset, you’ll see noticeable improvements in both your confidence and problem-solving skills.