Mastering mathematics involves understanding and applying a variety of problem-solving techniques. The exercises in this particular part offer a comprehensive overview of important concepts that will help you sharpen your skills and improve your grasp of mathematical reasoning.
With a systematic approach, these problems guide learners through progressively more challenging material. By practicing and analyzing solutions, students gain valuable insights that contribute to their overall academic development.
In this section, solutions are provided to assist in breaking down difficult problems and revealing the underlying patterns. Careful examination of each step can help build confidence and foster a deeper appreciation for the logic behind every calculation. Taking the time to study these solutions will not only improve accuracy but also enhance critical thinking skills.
Algebra Nation Answer Key Section 6 Guide
This part of the material focuses on helping learners navigate through more advanced mathematical exercises, providing detailed explanations for each problem. By following the steps outlined in the solutions, students can develop a clearer understanding of the methods used to reach the correct outcomes, ensuring a stronger foundation in key concepts.
Step-by-Step Walkthrough of Exercises
The provided solutions break down each problem into smaller, manageable steps. This approach allows students to grasp the logic behind each solution, encouraging better problem-solving strategies. With a focus on clarity and thoroughness, each step highlights the essential techniques necessary to complete similar tasks in the future.
Building Confidence Through Practice
Repetition is a powerful tool in mastering mathematical principles. By regularly referring to these detailed solutions, learners can boost their confidence and enhance their ability to tackle new challenges. Over time, the patterns and strategies become second nature, allowing students to solve problems more efficiently and accurately.
How to Use the Answer Key Effectively
To fully benefit from the solutions provided, it’s important to approach them with a thoughtful mindset. Instead of merely looking at the final results, focus on understanding the reasoning behind each step. This process helps reinforce your comprehension and allows you to apply similar methods in future exercises.
Start by attempting the problems on your own before reviewing the provided solutions. When you compare your work to the given answers, analyze where your approach might differ. This reflection can highlight areas for improvement, helping you avoid common mistakes and strengthening your overall skills.
Step-by-Step Solutions for Section 6
This part provides detailed guidance for tackling each problem through a clear, structured approach. By breaking down complex tasks into manageable steps, learners can better understand the process and logic required to arrive at the correct results. Each solution is carefully designed to show not only the final outcome but also the reasoning that supports it.
Understanding the Approach
Start by reviewing the first step in each solution. Focus on the method used and how it applies to the problem at hand. By understanding the technique behind each move, you’ll gain insight into how to approach similar problems independently. The key is to see each step as a building block that connects logically to the next.
Applying Techniques to New Problems
Once you have grasped the steps in the provided solutions, apply these strategies to new exercises. With practice, you will find that these methods become more intuitive, allowing you to solve problems faster and with greater confidence. Keep refining your skills by repeating the process and challenging yourself with increasingly difficult tasks.
Common Mistakes and How to Avoid Them
While working through mathematical problems, it’s easy to fall into certain traps that can lead to errors. Recognizing these common mistakes and understanding how to avoid them is essential for improving accuracy and building a stronger foundation in problem-solving.
Frequent Errors and How to Prevent Them
Here are some common mistakes students make and tips for avoiding them:
- Skipping Steps: It’s tempting to skip steps, especially when you’re confident in your skills. However, missing out on intermediate steps can lead to incorrect results. Always write out each part of the solution.
- Misinterpreting the Problem: Not fully understanding the question can cause confusion and lead to errors. Carefully read the problem and make sure you comprehend what is being asked before starting.
- Rushing Through Calculations: Speed is important, but precision is key. Double-check your calculations to avoid simple arithmetic mistakes.
Tips for Improving Accuracy
To minimize mistakes, keep the following strategies in mind:
- Review Each Step: Before moving on to the next part of the problem, review the current step to ensure it’s correct.
- Take Your Time: Don’t rush through the problems. Allocate enough time to understand and solve each question methodically.
- Practice Regularly: The more you practice, the more familiar you become with the common pitfalls, helping you avoid them in the future.
Understanding Key Mathematical Concepts
Grasping fundamental principles is crucial for solving complex problems effectively. By focusing on core concepts and their practical applications, learners can develop a deeper understanding and tackle a wider range of exercises with greater confidence. These essential ideas serve as the foundation for more advanced topics and are critical for mastering the subject.
Mastering Basic Problem-Solving Techniques
To build a solid foundation, it’s important to familiarize yourself with common techniques such as balancing equations, simplifying expressions, and factoring. These methods are central to solving most problems, and having a strong grasp of them will allow you to approach challenges with a structured mindset. Consistency in practice ensures these techniques become second nature.
Connecting Concepts for Greater Understanding
Understanding how different concepts relate to one another is vital. Recognize the links between various topics such as operations with numbers, the properties of functions, and the manipulation of variables. This interconnectedness allows you to apply the knowledge more flexibly across different scenarios and problem types.
Improving Your Math Skills with the Solutions
Improving your problem-solving abilities requires practice and effective guidance. By regularly reviewing the provided solutions, you can enhance your understanding of essential techniques and strengthen your approach to complex tasks. Over time, this practice will help you develop both speed and accuracy in solving similar problems independently.
Practical Ways to Enhance Your Skills
Here are some effective strategies to improve your math skills:
- Analyze Each Step Carefully: Rather than just looking at the final solution, break down the steps used to reach the answer. This helps reinforce your understanding of the underlying methods.
- Practice Regularly: Consistent practice is key to improving your abilities. Work through various problems, applying the same techniques to different types of exercises.
- Focus on Weak Areas: If certain concepts or methods are challenging, spend extra time reviewing them. Understanding where you struggle will help you target your practice more effectively.
Tracking Your Progress
As you continue practicing, it’s important to track your progress. Regularly test yourself on different problems and compare your results to the solutions provided. Over time, you should notice improvements in both the time it takes to solve problems and the accuracy of your solutions.
Breaking Down Complex Problems in Section 6
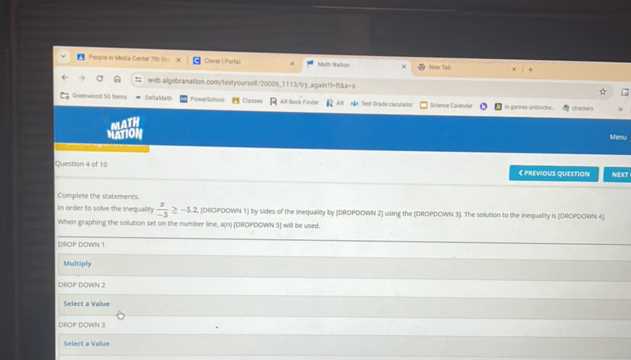
When tackling challenging problems, breaking them down into smaller, more manageable parts can make the process easier to understand and solve. This approach helps you focus on one step at a time, reducing the complexity and enabling you to approach each task methodically. By understanding the structure of the problem, you can find effective solutions more efficiently.
Step-by-Step Problem Decomposition
Start by carefully reading through the problem and identifying the key components. Look for the main question and the information provided. Break the problem into smaller parts, tackling each one individually. Focus on one operation at a time, whether it’s simplifying, factoring, or solving for a variable, and keep track of each intermediate result.
Identifying Patterns and Relationships
As you work through the problem, pay attention to any patterns or relationships between the different elements. Recognizing these connections can provide valuable insights and lead to quicker solutions. By identifying recurring techniques or similarities to previously solved problems, you can apply strategies that have proven effective in the past, improving both speed and accuracy.
What to Expect in Section 6

In this part of the material, you will encounter more challenging exercises that require a deeper understanding of the concepts introduced earlier. The problems are designed to test your ability to apply various techniques in new and unfamiliar contexts. Expect to encounter both familiar and novel situations that will push your problem-solving abilities to the next level.
The problems in this section will require you to carefully analyze the given information, break down complex tasks, and apply logical reasoning to reach the correct solutions. By completing these exercises, you will develop a better grasp of advanced methods and strategies, preparing you for even more difficult challenges in the future.
Detailed Solutions for Practice Exercises
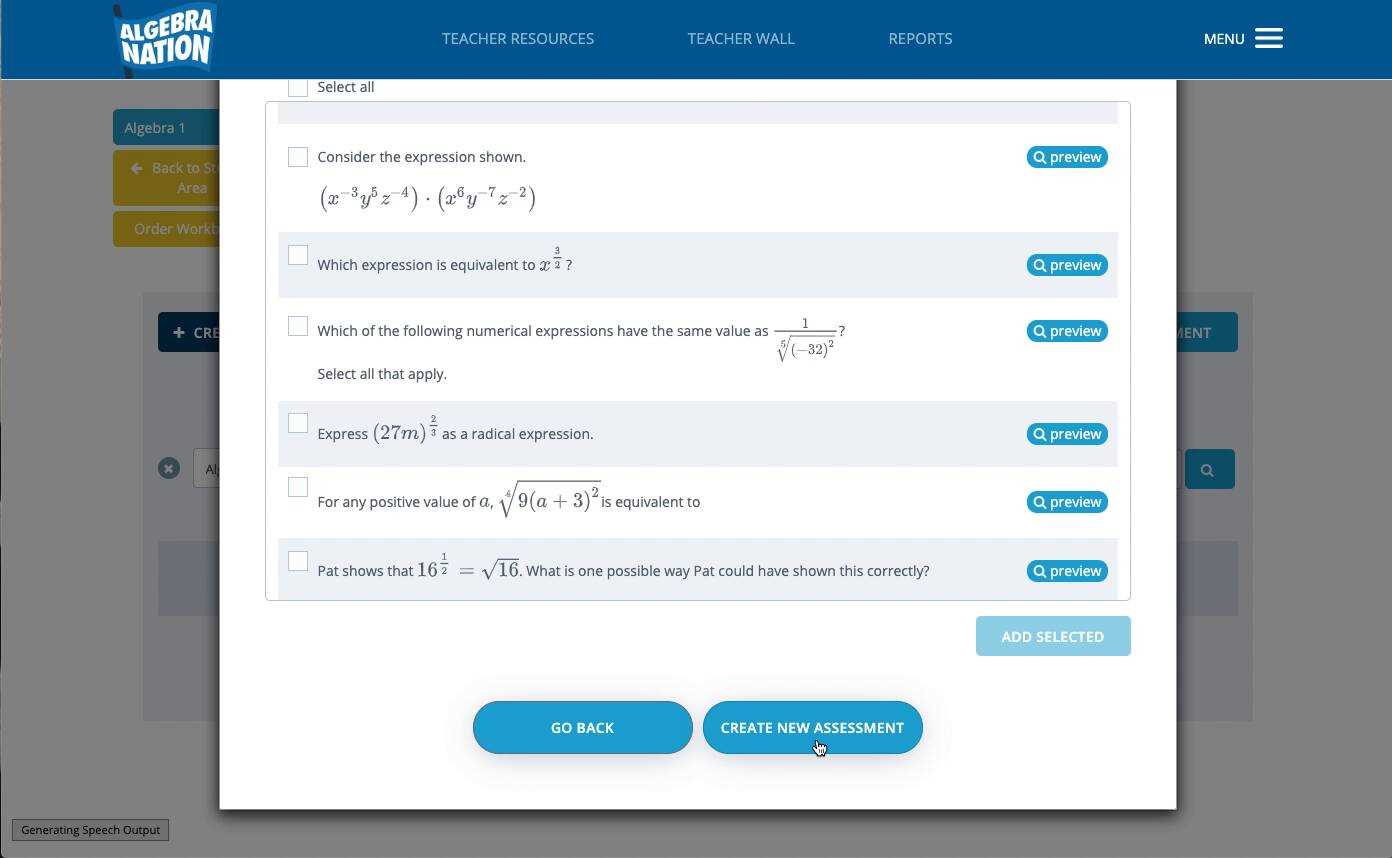
To master any topic, it’s essential to not only practice but also understand the reasoning behind each solution. In this section, you’ll find comprehensive explanations for the practice problems, breaking down each step clearly so you can follow along and learn the correct methods. These solutions aim to strengthen your problem-solving skills and help you gain a deeper understanding of the material.
How to Approach the Problems
Before jumping into the solutions, it’s important to have a strategy. Follow these steps for optimal learning:
- Read Carefully: Understand the problem before you attempt to solve it. This will prevent common mistakes and help you identify what’s being asked.
- Break It Down: Divide the problem into smaller parts to make it more manageable. Solve each part individually, then combine them for the final answer.
- Check Your Work: Always review your calculations to ensure accuracy and understand why certain methods were used.
Step-by-Step Solutions
Each problem has been broken down into clear, step-by-step solutions, helping you understand the logic behind each operation:
- Step 1: Begin by simplifying the problem. Identify the variables and constants, and isolate the unknowns.
- Step 2: Use appropriate methods, such as factoring, substitution, or elimination, depending on the type of problem.
- Step 3: Solve for the unknown and check the result by substituting it back into the original equation.
By following these steps, you’ll develop the confidence and skills necessary to tackle even the most challenging exercises independently.
Tips for Quick Problem Solving

Solving problems quickly and accurately is a valuable skill that can be developed with practice and strategy. By employing effective techniques and understanding key patterns, you can enhance your ability to solve complex tasks in less time while maintaining precision. This section provides useful tips to help you streamline your problem-solving process and improve efficiency.
Key Strategies for Faster Solutions

When you’re faced with a problem, try using these methods to increase your speed and accuracy:
- Prioritize Simplicity: Break complex problems into simpler parts. Focus on the core steps and avoid overcomplicating the task.
- Look for Patterns: Recognizing patterns in the problem can lead to faster solutions. Often, similar problems share the same solving techniques.
- Use Estimation: Before solving, quickly estimate an answer to get a sense of whether your final result makes sense.
Efficient Problem Solving Techniques
Here is a table of common techniques that can speed up your problem-solving process:
| Technique | When to Use | Benefit |
|---|---|---|
| Elimination | When solving systems of equations | Quickly removes variables, simplifying the process |
| Substitution | When one equation is easy to solve for a variable | Provides a direct method for finding solutions |
| Factoring | For quadratic expressions | Helps simplify expressions, speeding up calculations |
By incorporating these techniques into your practice, you’ll be able to solve problems more effectively and reduce the time it takes to reach a solution.
Using the Platform for Self-Study
The platform provides an excellent opportunity for independent learning, offering a range of resources that allow you to practice and reinforce your understanding of various concepts at your own pace. By using the material effectively, you can tailor your study plan to address your weaknesses and reinforce your strengths. This method of self-guided learning promotes deeper understanding and greater retention of key concepts.
Maximizing Your Learning Experience
To make the most of this self-study approach, consider these strategies:
- Set Clear Goals: Identify specific areas you want to focus on, whether it’s mastering a certain technique or improving problem-solving speed.
- Practice Regularly: Consistency is key. Regular practice ensures that concepts are retained and applied effectively when solving problems.
- Review Mistakes: When you make errors, take the time to understand them. This will help you avoid similar mistakes in the future and improve your approach.
Tracking Your Progress
As you work through the material, track your progress to stay motivated and identify areas where you may need additional review. This can be done by:
- Using quizzes and tests: These help assess your understanding and highlight areas for improvement.
- Noting areas of difficulty: Keep a list of challenging topics to revisit after some time for better comprehension.
By following these strategies, you can create a structured and efficient self-study routine that enhances your learning and ensures steady progress.
Enhancing Your Knowledge with Section 6
Section 6 offers an invaluable opportunity to deepen your understanding of core mathematical concepts and improve your problem-solving abilities. By thoroughly engaging with the material, you can develop stronger skills that will allow you to tackle increasingly complex tasks with ease. This section provides a structured way to explore and master essential principles, reinforcing your learning and boosting your confidence.
Key Areas of Focus
To maximize your learning, it’s important to focus on the key areas covered in this section. Here’s a breakdown of the major concepts you’ll encounter:
| Concept | Description | Why It’s Important |
|---|---|---|
| Equations | Understanding how to solve various types of equations. | Mastering equations is fundamental for solving more complex problems. |
| Graphing | Learning to plot points and interpret graphs. | Graphing helps visualize relationships and trends, making abstract ideas more tangible. |
| Functions | Exploring different types of functions and their properties. | Functions are the backbone of many advanced mathematical topics and real-world applications. |
By engaging with these concepts and practicing regularly, you’ll be able to reinforce your understanding and apply these skills to various challenges. This section serves as a great tool for building a strong mathematical foundation that you can rely on as you progress in your studies.
Best Practices for Learning Mathematical Concepts
Mastering mathematical principles requires more than just memorizing formulas. It involves understanding the relationships between different elements and applying that knowledge to solve problems effectively. By adopting best practices, you can enhance your learning experience and achieve a deeper understanding of the material, making complex topics more accessible and manageable.
Effective Study Habits
Establishing consistent study routines and employing strategies that cater to your learning style can significantly improve your grasp of mathematical concepts. Consider the following techniques:
- Practice Regularly: Consistent practice helps reinforce understanding and ensures concepts are retained over time.
- Break Down Problems: Tackle problems in smaller, manageable parts to avoid feeling overwhelmed and to build your skills step by step.
- Seek Understanding, Not Memorization: Focus on comprehending the reasoning behind formulas and operations rather than memorizing them by rote.
- Review Mistakes: Analyze errors and understand why they occurred. This will deepen your understanding and prevent repeating them.
Utilizing Resources Effectively
Leveraging various resources can provide valuable support in your learning process. Some methods include:
- Online Tools and Exercises: Interactive platforms and practice problems allow for hands-on learning and immediate feedback.
- Study Groups: Collaborating with peers allows for the exchange of ideas and diverse approaches to problem-solving.
- Textbooks and Notes: Reviewing theory and worked-out examples helps solidify your understanding before tackling problems independently.
By implementing these best practices and staying consistent with your efforts, you will gradually build a solid foundation in mathematics and be well-equipped to solve complex problems with confidence.
Test Preparation with Educational Resources
Preparing for a test involves more than just reviewing notes; it requires focused practice and a solid understanding of the concepts being tested. By using the right resources, you can enhance your preparation and ensure you approach the exam with confidence. One effective strategy is to utilize practice materials that offer detailed solutions and explanations, helping you refine your problem-solving skills and identify areas needing further improvement.
How to Use Practice Materials Effectively
Practice exercises are essential in reinforcing what you’ve learned and improving test-taking skills. To make the most of them:
- Work Through Each Problem: Don’t just look at the solution; attempt to solve the problem on your own first to reinforce your understanding.
- Focus on Problem Types: Identify common problem types that appear frequently in tests and ensure you’re comfortable solving them.
- Understand the Process: Pay attention to the methods and steps used to reach the solution. It’s important to grasp the reasoning behind each step.
- Revisit Mistakes: Review incorrect solutions carefully to understand where you went wrong and learn from your mistakes.
Maximizing Learning with Feedback
Getting feedback on your practice work is crucial for improvement. Here’s how feedback can help:
- Identify Weak Areas: Use feedback to pinpoint specific concepts or types of problems you need to work on more.
- Track Progress: Regular feedback helps you track your progress over time, allowing you to adjust your study strategy accordingly.
- Refine Strategies: Continuous feedback encourages you to tweak your approach, whether it’s focusing more on specific techniques or adjusting your study schedule.
By following these strategies and consistently practicing with helpful resources, you’ll be well-prepared for any exam and more confident in your ability to solve complex problems effectively.
Why Educational Resources Are an Effective Tool
Using well-designed educational platforms can significantly enhance the learning process by providing structured support, practical exercises, and immediate feedback. These resources are designed to address various learning needs, from foundational concepts to more advanced topics, making them ideal for students at different levels. By focusing on detailed problem-solving techniques, these tools help learners gain confidence and mastery over the subject matter.
One of the key advantages of these platforms is their ability to offer personalized learning experiences. They cater to individual learning speeds and provide targeted practice based on specific areas of difficulty. Whether you’re looking to reinforce basic concepts or tackle more complex problems, these resources allow for focused and efficient study sessions.
Additionally, they often incorporate features such as interactive exercises, step-by-step solutions, and progress tracking, all of which make the learning experience more engaging and effective. By offering immediate feedback, students can quickly understand where they may have gone wrong and make adjustments, ultimately leading to better retention and a deeper understanding of the material.
In summary, educational tools like this provide a comprehensive approach to learning, offering students the opportunity to build a strong foundation while honing their problem-solving skills. This makes them an invaluable resource for anyone looking to improve their skills and perform better in assessments.