
Mastering complex mathematical tasks requires a strong grasp of various concepts that are essential for solving intricate puzzles. These skills are vital for navigating through various challenges that test one’s ability to reason, visualize, and think critically. By developing the right approach, anyone can tackle difficult questions with confidence.
Effective problem-solving involves not only applying known techniques but also understanding how to adapt strategies based on the problem at hand. The key is to break down the task into manageable steps and recognize patterns that simplify the process.
Visual aids and logical reasoning play a significant role in making abstract concepts clearer, allowing for easier solutions. Whether you’re dealing with theoretical exercises or practical scenarios, these tools will help sharpen your ability to think analytically and solve problems efficiently.
Cpm Geometry Connections Answers
In mathematical exercises, it’s essential to understand how different elements relate to each other. The ability to identify patterns and apply appropriate methods can significantly streamline the solving process. This section will guide you through effective strategies and step-by-step solutions for tackling complex problems that involve various types of relationships between figures.
By breaking down each problem into smaller, more manageable parts, you can focus on understanding the underlying principles and applying the correct approach. Recognizing key relationships and leveraging geometric reasoning will help simplify the process and make finding solutions much easier.
- Step 1: Identify the variables and the relationships between them.
- Step 2: Use diagrams or models to visualize the problem clearly.
- Step 3: Apply known formulas and adjust them according to the given information.
- Step 4: Double-check the solution by verifying all the steps and calculations.
It is crucial to maintain a logical progression throughout the solving process. Focus on each stage individually to ensure that no details are overlooked. With consistent practice, these techniques will help you develop a deep understanding of the concepts and improve your ability to solve similar problems in the future.
Understanding Key Concepts in CPM Geometry

Grasping the fundamental principles of spatial relationships is crucial for solving complex mathematical problems. By focusing on the basic building blocks, one can better understand how various elements interact within a given problem. This section delves into these essential ideas and offers a clear path to mastering the skills necessary for advanced tasks.
One of the key approaches to success is recognizing patterns and knowing how to manipulate them based on the context. Whether dealing with shapes, lines, or angles, a systematic approach helps simplify otherwise challenging concepts.
| Concept | Description | Importance |
|---|---|---|
| Shape Properties | Understanding the unique characteristics of different figures. | Helps identify key features for solving problems involving specific shapes. |
| Angle Relationships | Knowing how angles relate to each other within a figure. | Crucial for calculating unknown angles or solving for missing components. |
| Area and Perimeter | Calculating the size and boundaries of figures. | Essential for determining spatial dimensions and solving practical problems. |
Once these core concepts are understood, it becomes easier to apply them effectively in various scenarios. By refining your ability to think critically and logically, solving intricate problems becomes more intuitive.
How to Solve Geometry Connections Effectively
Solving complex spatial problems requires a structured approach that focuses on understanding relationships between elements and applying logical steps. By following a systematic method, you can break down challenging tasks into manageable parts and solve them more efficiently. This section outlines key strategies for mastering these types of problems with confidence and precision.
To solve these problems effectively, it is essential to follow a clear sequence of steps. Here are some of the most important strategies to consider:
- Start with a clear diagram: Visualizing the problem is often the first step to understanding the relationships between different components. Draw accurate sketches to map out the elements and their connections.
- Identify known and unknown elements: Determine what information is given and what needs to be found. This helps focus on the critical aspects of the problem and eliminates distractions.
- Use logical reasoning: Apply basic principles, such as symmetry or proportionality, to find connections between different parts of the figure. This can often simplify the problem.
- Break the problem into smaller steps: Divide the task into smaller, more manageable sections to avoid feeling overwhelmed. Solve each part step-by-step before combining them for the final solution.
- Verify your solution: After solving the problem, double-check your work to ensure accuracy. Revisit your diagram and confirm that all steps were followed correctly.
By following these steps and practicing regularly, you can improve your ability to solve spatial problems more efficiently. The key to success lies in understanding the relationships between elements and using clear, logical methods to derive the solution.
Common Mistakes in Geometry Problems
When solving spatial tasks, it’s easy to make mistakes that can lead to incorrect results. Understanding the common errors and knowing how to avoid them is essential for improving problem-solving skills. This section outlines frequent missteps that can occur during calculations and reasoning, offering tips on how to prevent them.
Misinterpreting the Problem

A common error is misreading the problem or overlooking crucial details. Sometimes, the wording of a question can be confusing, or essential information may be hidden within a complex statement. It’s important to carefully read the problem and identify all given data before proceeding.
Incorrect Use of Formulas
Using formulas incorrectly is another frequent mistake. Whether it’s a wrong formula or improper application, incorrect use of mathematical expressions can lead to faulty results. Always ensure you are using the right equation for the specific task at hand.
| Common Mistake | Cause | Solution |
|---|---|---|
| Misinterpreting Angles | Confusing complementary or supplementary angles. | Carefully review angle relationships and double-check calculations. |
| Skipping Steps | Rushing through a problem without following each step. | Take your time and follow a clear step-by-step approach. |
| Overlooking Units | Not converting or checking units of measurement. | Ensure all units match and conversions are made where necessary. |
Avoiding these common mistakes can significantly improve your accuracy when tackling spatial challenges. With careful attention to detail and a methodical approach, you can minimize errors and achieve reliable results every time.
Tips for Mastering Geometry Connections
Mastering spatial problems requires a combination of practice, strategic thinking, and the ability to recognize key relationships between elements. With the right approach, anyone can improve their problem-solving skills and gain confidence in tackling complex tasks. This section provides effective strategies to help you master the key skills needed for success.
Focus on Visualizing the Problem
One of the most important steps in solving these problems is visualizing the given information. Creating accurate diagrams or sketches will help you better understand the spatial relationships and make it easier to identify patterns. This step not only clarifies the problem but also allows you to see potential solutions more clearly.
Develop a Systematic Approach
A systematic approach is essential for tackling complicated problems. Start by breaking the task into smaller, manageable steps. Focus on understanding the relationships between each component before applying any formulas. This method ensures that you don’t overlook important details and helps you stay organized throughout the process.
Additionally, reviewing past problems and solutions is a great way to reinforce these skills. Regular practice builds familiarity with common problem types, enabling you to approach new challenges with greater ease.
Step-by-Step Guide to Geometry Solutions
To solve spatial problems effectively, it’s essential to follow a clear, structured process. By breaking down the task into manageable steps, you can ensure that no detail is overlooked and that each part of the problem is addressed systematically. This guide provides a simple approach that can help you solve complex problems with confidence and accuracy.
Step 1: Understand the Problem
Before you begin solving, take the time to fully understand the question. Identify what information is given and what you are asked to find. This step is critical for setting up the correct approach and ensuring that you don’t miss any important details.
Step 2: Draw a Diagram or Model
Creating a clear diagram or model of the problem can significantly simplify the process. Visualizing the elements involved allows you to see relationships and identify key components. Make sure your diagram is accurate and reflects the details described in the problem.
Once your diagram is ready, proceed step-by-step, applying logical reasoning and appropriate methods to solve the problem. After completing the task, verify the solution by rechecking each step and confirming that everything aligns with the given information.
Importance of Geometry in Problem-Solving
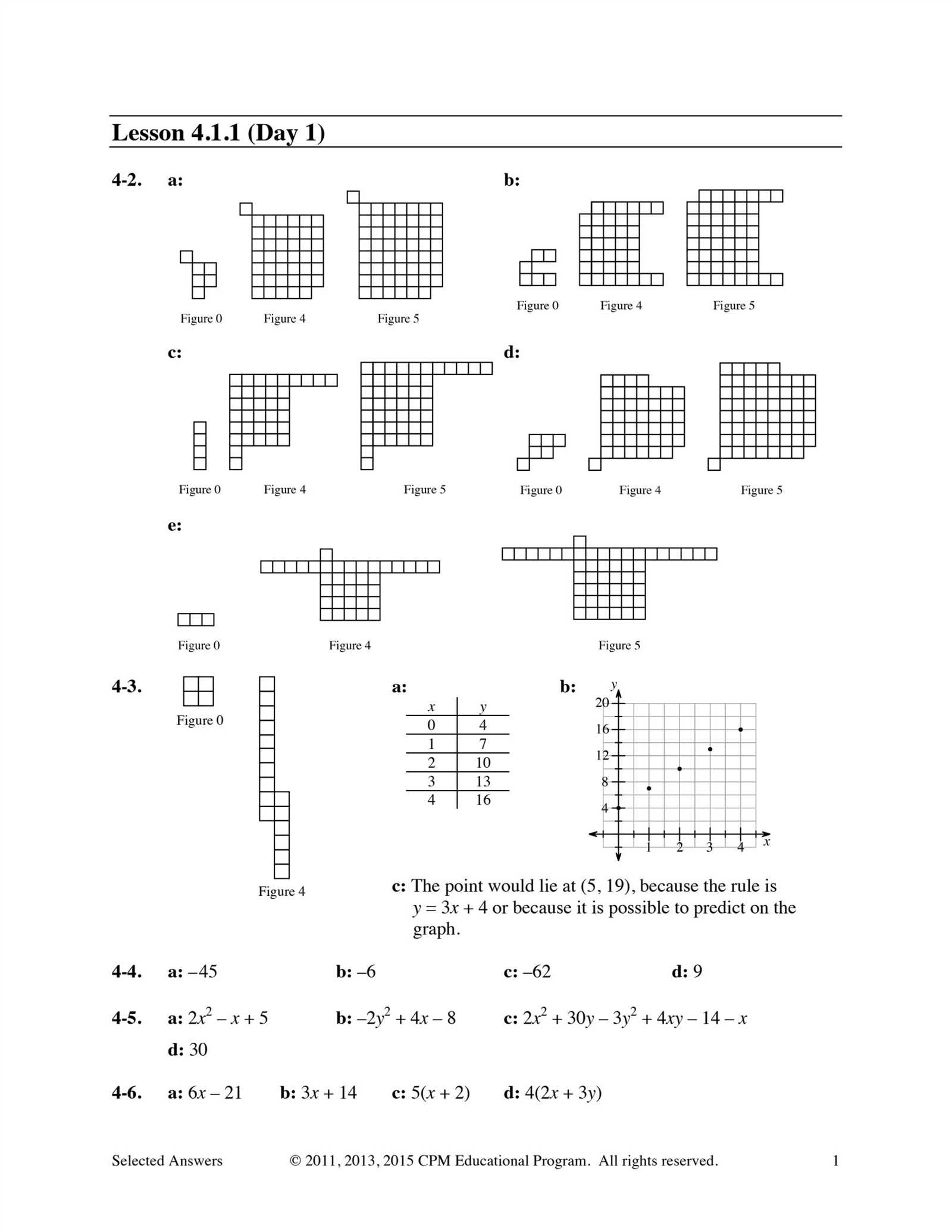
Understanding spatial relationships is vital when solving complex problems across various fields. The ability to think critically and visualize elements interacting with each other helps break down intricate tasks into manageable components. This skill is essential not only for mathematical challenges but also for practical decision-making and everyday applications.
Here are several reasons why this knowledge is crucial in problem-solving:
- Enhances Analytical Thinking: Visualizing the connections between different elements encourages logical reasoning and helps structure solutions more effectively.
- Improves Spatial Awareness: The ability to understand how objects relate in space is fundamental for solving real-world problems, such as designing structures or navigating spaces.
- Facilitates Pattern Recognition: Identifying recurring patterns and relationships between figures makes complex tasks easier to approach and solve.
- Broadens Problem-Solving Skills: Understanding the principles of spatial reasoning provides the foundation for solving a wide range of problems in science, engineering, and technology.
Incorporating these skills into problem-solving strategies leads to more efficient, accurate, and creative solutions. Whether working through academic tasks or addressing practical issues, the ability to manipulate and understand spatial elements is invaluable for success.
Breaking Down Complex Geometry Connections
When faced with intricate spatial problems, the key to finding a solution lies in simplifying the task. Breaking down complex relationships into smaller, manageable steps allows you to tackle each part individually, making it easier to identify patterns and apply appropriate methods. This approach helps reduce confusion and enables a clearer understanding of how the elements interact.
One effective strategy for handling complicated tasks is to start by identifying the most basic components. Focus on understanding the fundamental properties and relationships of each figure involved. Once you have a clear grasp of these, you can begin to connect them logically, step by step.
Another important technique is to break the problem into smaller subproblems. By addressing each part separately, you can solve them independently before combining the solutions to form the complete answer. This method helps avoid overwhelming yourself with the complexity of the entire task at once and ensures a more accurate result.
With practice and a systematic approach, even the most complicated challenges can be simplified and solved effectively. The key lies in breaking down the problem, understanding the relationships between components, and applying logical reasoning to solve each part sequentially.
Visualizing Geometry Connections for Success
Effective problem-solving often depends on how well we can visualize complex relationships and structures. The ability to mentally picture how different elements interact with each other helps break down complicated tasks into simpler steps. This skill is particularly useful when working with intricate problems that involve multiple components and relationships.
Creating a clear mental image of the figures and their connections allows you to better understand how they relate. By seeing the bigger picture, you can identify patterns and structures that may not be immediately obvious. This enhances your ability to apply the correct methods and make informed decisions when solving the problem.
In many cases, drawing diagrams or models can further solidify your understanding. These visual tools serve as a reference, making it easier to track relationships and spot potential errors. With practice, visualizing these connections becomes second nature, enabling you to approach complex challenges with confidence and precision.
Ultimately, developing the ability to visualize spatial relationships will not only improve your problem-solving skills but also make tackling advanced tasks more intuitive and efficient.
Strategies for Tackling Difficult Geometry Questions
When faced with challenging spatial problems, it’s important to approach them systematically. Difficult tasks often require a deeper level of understanding and the ability to apply multiple strategies. By breaking down the problem into smaller, manageable parts, you can tackle it step by step and increase your chances of finding a solution. Here are a few strategies that can help guide you through tough problems.
Start with the Basics

Before diving into complex calculations or theories, ensure you understand the foundational elements of the problem. Identify key components, such as points, lines, angles, or shapes, and recall any relevant properties. Sometimes, starting with simple relationships can provide valuable insights that lead to a solution.
Use a Structured Approach
Break the problem down into smaller steps. Work through each part in a logical sequence, using known formulas or theorems to address each individual component. This step-by-step approach will help prevent confusion and ensure that you don’t overlook any important details.
Additionally, don’t hesitate to sketch diagrams, create models, or write out intermediate steps. Visualizing the problem can often reveal patterns and relationships that might not be immediately obvious, leading you closer to the solution.
How to Use Diagrams in Geometry Problems
Diagrams are powerful tools for solving spatial problems. By visually representing the elements and their relationships, diagrams can help clarify complex situations, making it easier to understand and solve the problem. A well-drawn diagram can provide insight into the structure of the problem and guide you toward the correct solution.
Start by carefully reading the problem to identify the key components, such as shapes, angles, and points. Once you have a clear understanding, sketch a diagram that accurately reflects the information provided. Ensure that all necessary details, such as labels, measurements, and any given values, are included in your drawing. The clearer the diagram, the easier it will be to apply the appropriate mathematical principles.
In some cases, a diagram may reveal patterns or relationships that aren’t immediately obvious from the problem statement alone. These visual cues can help you make connections between different parts of the problem, allowing you to apply geometric properties or theorems that might be useful for finding the solution.
Additionally, diagrams can serve as a reference throughout the problem-solving process. As you work through the problem, refer back to the diagram to ensure that your steps align with the visual representation. This can help prevent errors and keep you on track toward the correct answer.
Geometry Connection Techniques for Beginners
When starting out with spatial problems, it can be difficult to see how different elements are related. Developing a strong understanding of the basic techniques for connecting various shapes, lines, and angles will help you build a solid foundation for tackling more complex tasks. By using systematic methods, beginners can begin to identify patterns and apply key concepts to solve problems efficiently.
One of the most important techniques for beginners is learning how to break down a problem into smaller, simpler parts. This allows you to focus on one relationship or component at a time, making the entire problem easier to handle. Below are some effective strategies to help you establish strong connections between elements:
| Technique | Description |
|---|---|
| Draw Clear Diagrams | Start by sketching the problem to visually represent the components involved. Label all important elements to create a clearer understanding of the relationships between them. |
| Identify Known Values | Highlight any known measurements or properties. This will allow you to establish starting points for applying relevant formulas or theorems. |
| Use Logical Steps | Break down the problem into manageable steps. Approach each element methodically, solving smaller parts before tackling the entire problem. |
By mastering these fundamental techniques, you’ll develop the skills needed to make sense of complex tasks. The key to success is practice and building confidence in applying these methods to different types of problems.
Analyzing Different Geometry Problem Types
When working with spatial challenges, it’s crucial to recognize the different types of problems you may encounter. Each type has unique characteristics and requires a distinct approach for effective problem-solving. By understanding these variations, you can apply the appropriate techniques to find solutions more efficiently. Below, we explore some common problem types and the strategies best suited for each.
Classification of Common Problem Types
Problems can be grouped into several categories based on their characteristics. The more familiar you become with these types, the better you can adapt your approach to each scenario.
| Problem Type | Description | Strategy |
|---|---|---|
| Measurement Problems | These problems involve finding specific dimensions or angles of shapes based on given information. | Use formulas for area, perimeter, and angles. Label all known values clearly and apply relevant principles. |
| Proof Problems | Proof-based problems require showing that a specific geometric statement is true based on known theorems and axioms. | Start with what is given, and build a logical argument using known geometric properties and postulates. |
| Construction Problems | In these, you are tasked with creating a figure based on certain criteria or instructions. | Use compass and straightedge techniques. Focus on accuracy and following the step-by-step process. |
Strategies for Approaching Different Problems
Understanding the structure of each problem type allows you to select the most appropriate method for solving it. Whether it’s applying geometric principles, drawing diagrams, or using logical reasoning, having a strategy in place is key to success.
As you gain more experience, these approaches will become second nature, allowing you to approach each problem with confidence and clarity.
Advanced Methods for Solving Geometry Problems
As you progress in solving spatial challenges, you may encounter more complex problems that require advanced strategies and techniques. These methods involve a deeper understanding of the principles, along with creative approaches to problem-solving. Developing proficiency with these techniques allows you to tackle sophisticated tasks with greater efficiency and precision.
Key Advanced Techniques

Advanced strategies often involve leveraging multiple concepts simultaneously or using higher-level tools to simplify complex problems. Below are some methods that can be helpful:
- Coordinate Geometry: This method involves placing shapes on a coordinate plane and using algebraic equations to solve for unknown values, making it easier to work with complex shapes.
- Transformations: By applying rotations, reflections, and translations, you can manipulate figures to find symmetries or solve for unknowns.
- Trigonometry: For problems involving angles, trigonometric ratios like sine, cosine, and tangent can be used to find missing sides or angles in right triangles.
- Vector Analysis: Vectors can be used to solve problems involving direction and magnitude, particularly in three-dimensional spaces or for finding relationships between different shapes.
Effective Problem-Solving Process
To efficiently apply these advanced methods, it’s important to break down the problem and follow a structured approach:
- Identify Known and Unknown Variables: Understand what is given and what you need to find.
- Choose the Right Method: Based on the problem type, select the most suitable advanced technique to apply.
- Work Step by Step: Solve the problem in smaller, manageable steps, verifying each solution before moving on.
- Check for Consistency: Once you find a solution, double-check your work to ensure all calculations and logic hold true.
By mastering these advanced techniques, you can confidently solve more intricate and challenging problems. Consistent practice and experience will refine your problem-solving abilities, helping you approach each challenge with the tools necessary for success.
Practical Applications of Geometry Connections
Understanding the relationships between shapes and their properties is essential not only in academic settings but also in real-world scenarios. By applying these concepts effectively, individuals can solve problems across various fields, from architecture to technology and engineering. Mastering these relationships allows us to model physical spaces, optimize designs, and develop innovative solutions to complex challenges.
One of the most significant benefits of understanding spatial relationships is its widespread use in numerous industries. For example, architects rely on geometric principles to design buildings that are structurally sound and aesthetically pleasing. Engineers use similar concepts to develop efficient systems and machinery, while computer scientists apply spatial reasoning in areas like computer graphics and game development.
In addition to the built environment, these principles also play a crucial role in areas such as navigation and mapping. Understanding how different locations relate spatially allows for the creation of accurate maps and reliable GPS systems. Similarly, professionals in logistics and transportation use these techniques to optimize routes and minimize travel time, benefiting both businesses and consumers.
As technology advances, the application of these ideas continues to evolve. For instance, in the field of virtual reality, designers use spatial algorithms to create immersive and realistic environments. In medicine, imaging techniques such as MRI and CT scans rely on an understanding of three-dimensional spaces to generate accurate representations of the human body.
In summary, the ability to apply concepts related to spatial relationships is not only fundamental in solving theoretical problems but also has a profound impact on many aspects of our daily lives. By mastering these principles, individuals can contribute to fields that shape our world and drive innovation.
Geometry Connections in Real-World Scenarios
Spatial reasoning and the understanding of how shapes interact with one another play a significant role in many everyday applications. These principles are not confined to academic problems but are actively used to solve practical challenges across various industries. From the design of buildings to the creation of efficient transportation networks, the ability to visualize and apply these connections leads to tangible solutions that affect our daily lives.
Architectural Design and Construction
In architecture, understanding how different structures and spaces relate to each other is fundamental. Architects rely heavily on the knowledge of shape relationships to create buildings that are both functional and safe. By recognizing the way angles, distances, and dimensions interact, designers can create layouts that optimize space, ensure stability, and meet aesthetic standards. The use of advanced software allows for more precise designs, but at the heart of it is a deep understanding of how geometric elements work together.
Urban Planning and Infrastructure

Urban planners also use spatial reasoning to design cities that are efficient and sustainable. This includes everything from traffic flow and public transportation networks to the layout of utilities and green spaces. By analyzing how different regions within a city relate spatially, planners can create systems that reduce congestion, ensure accessibility, and improve overall quality of life. The careful consideration of these relationships ensures that cities are not just functional, but also livable and well-connected.
Beyond urban spaces, industries such as manufacturing, technology, and even healthcare depend on spatial thinking. In manufacturing, for instance, the layout of machines and assembly lines requires careful planning of how objects move through space. In healthcare, the interpretation of medical images and the precise placement of equipment in operating rooms are also dependent on these concepts. These real-world applications demonstrate how an understanding of shapes and spatial relationships is fundamental to solving complex, everyday problems.
Tools to Enhance Geometry Problem Solving
In tackling complex spatial challenges, using the right tools can make a significant difference in solving problems efficiently and accurately. Whether you are working on abstract theoretical concepts or real-world applications, having access to various instruments and resources can improve your problem-solving skills. These tools range from traditional methods to modern technological innovations, all designed to help visualize, analyze, and solve intricate spatial relationships.
Traditional Tools
While digital tools are incredibly helpful, traditional instruments still play a crucial role in understanding and solving spatial problems. Some of these tools include:
- Compass: Useful for drawing precise circles and arcs, essential for many constructions.
- Protractor: Helps measure and construct accurate angles, which is vital in numerous geometric proofs and constructions.
- Ruler: A fundamental tool for measuring distances and drawing straight lines in geometric diagrams.
- Graph Paper: Provides a grid for plotting points, lines, and curves, helping visualize relationships between shapes.
Technological Tools
In today’s digital age, various software and applications can significantly enhance problem-solving capabilities by offering interactive features and more advanced visualization. Some useful technological tools include:
- Geogebra: A dynamic mathematics software that combines geometry, algebra, and calculus, making it easy to visualize and manipulate geometric constructions.
- Sketchpad: Another powerful tool for constructing geometric shapes and exploring their properties, allowing for more intuitive learning and problem-solving.
- 3D Modeling Software: Programs like AutoCAD or SolidWorks are used for visualizing and designing objects in three dimensions, helpful for understanding complex spatial relationships in both engineering and design.
- Graphing Calculators: These devices are essential for plotting functions and analyzing geometric shapes, often with advanced features like 3D graphing.
Incorporating these tools into your problem-solving routine can help build a deeper understanding of spatial concepts, making it easier to tackle even the most challenging problems with confidence and clarity.
Improving Accuracy in Geometry Connections
Achieving precision in spatial problem-solving is crucial for obtaining reliable results. Whether you’re working with abstract theoretical problems or practical applications, small errors in measurements, construction, or reasoning can lead to incorrect conclusions. To enhance accuracy, it is important to follow systematic approaches, use appropriate tools, and double-check calculations. The strategies outlined below are designed to help minimize errors and improve overall precision in solving complex problems.
Key Techniques for Enhancing Precision
By focusing on careful execution and using specific techniques, you can significantly improve the accuracy of your work. Some effective methods include:
- Double-Check Measurements: Ensure that every length, angle, or distance is measured twice to avoid mistakes. Small inaccuracies can accumulate and affect the final outcome.
- Use High-Quality Tools: Investing in reliable and precise instruments like protractors, rulers, and compasses can help you avoid errors caused by faulty or imprecise tools.
- Follow a Step-by-Step Process: Breaking down the problem into manageable steps ensures that each part is addressed thoroughly. Skipping steps or rushing can introduce mistakes.
- Use Visual Aids: Drawing diagrams and sketches can make complex relationships clearer and reduce the chance of misunderstanding or misinterpreting information.
- Verify Results: After reaching a solution, revisit the problem to ensure the solution makes sense within the context. Cross-referencing with known formulas and properties can confirm accuracy.
Utilizing Technology for Better Accuracy
In addition to traditional methods, modern tools and technology can greatly enhance precision. The following tools are particularly useful for improving accuracy:
- Computer Software: Programs like GeoGebra or SketchUp allow for precise measurements and allow you to visualize complex shapes and transformations with greater ease.
- Digital Calipers: These tools offer incredibly accurate measurements for small distances, which is especially useful when dealing with intricate geometric figures.
- Graphing Calculators: Advanced graphing calculators help plot points and curves with high precision, reducing the likelihood of errors in visual representation.
- 3D Modeling Tools: Software designed for 3D visualization, such as AutoCAD, can help you view relationships in three-dimensional space, ensuring more accurate analysis of complex shapes.
By combining traditional methods with modern technological tools, and consistently applying accurate techniques, you can significantly improve the precision of your problem-solving process.