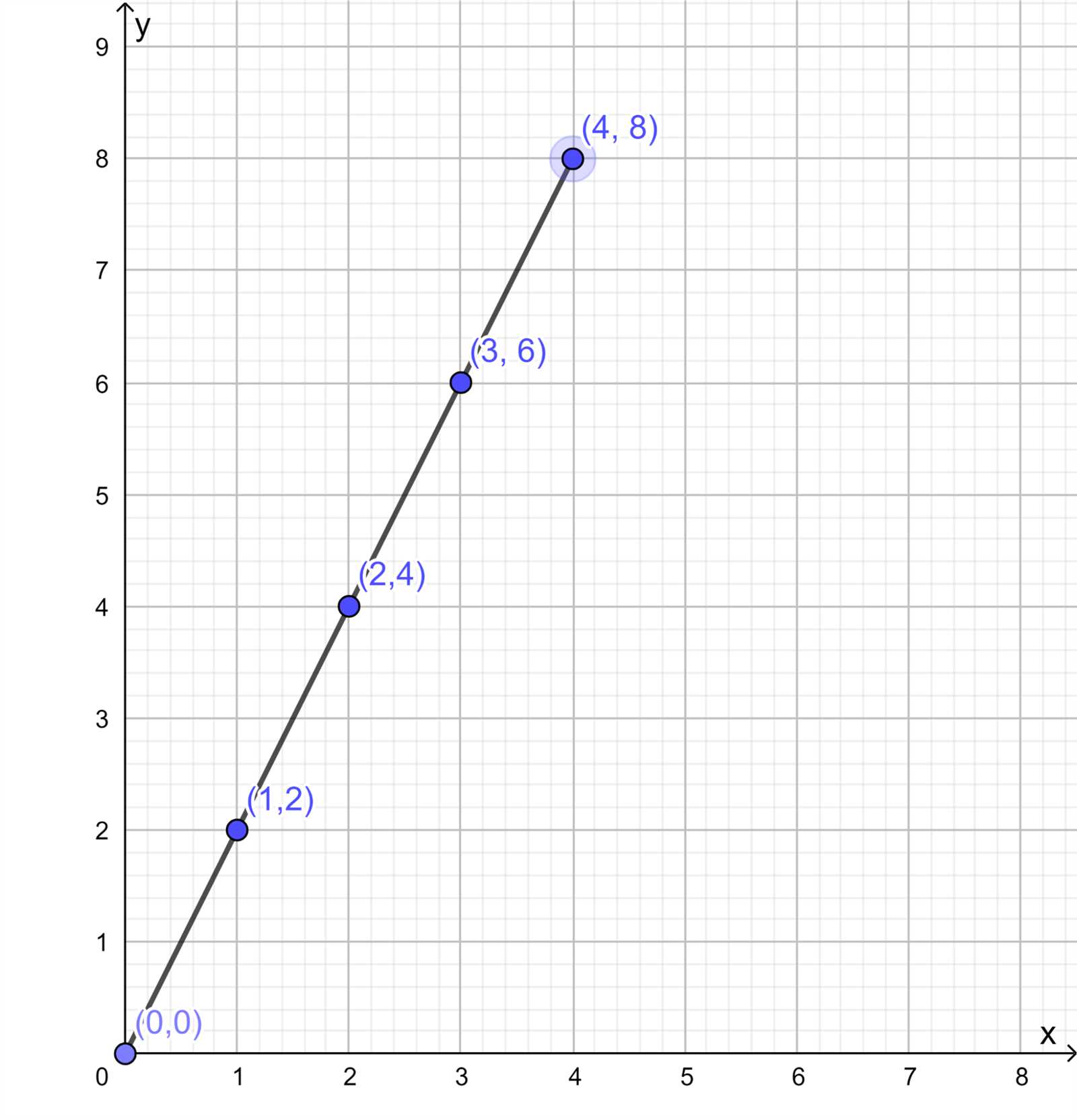
In this section, we explore fundamental principles that are essential for understanding various mathematical scenarios. These concepts play a significant role in solving real-world problems by connecting different numerical values and their relationships. By mastering these ideas, students can gain a deeper insight into how numbers interact in both abstract and practical situations.
As we dive deeper, you’ll learn how to identify key patterns and structures that allow for consistent mathematical reasoning. This knowledge will provide a foundation for tackling more complex problems, especially in fields such as geometry, algebra, and data analysis. Grasping these core principles is not only vital for academic growth but also beneficial in everyday problem-solving scenarios.
Course 3 Chapter 3 Proportional Relationships and Slope Answers
This section focuses on key mathematical concepts that involve comparing quantities and understanding how they relate to each other through linear models. The ideas presented here are crucial for solving a wide range of problems where two variables are linked, and their rate of change can be determined.
To help you fully grasp these concepts, we will explore various methods and techniques for solving problems that involve direct and constant variation. Understanding the rules that govern these interactions is essential for successfully working through related exercises.
- Learn how to recognize when two quantities are linked in a way that their values consistently increase or decrease together.
- Master the skills necessary to calculate the rate of change between two variables, and how this value reflects the relationship between them.
- Understand how to interpret visual representations, such as graphs, to identify key features like rate and direction of change.
By the end of this section, you will be able to apply these principles to solve problems with varying levels of complexity. The ability to work with these concepts is an important foundation for further study in mathematics and other related fields.
- Review how to calculate the rate of change for different types of problems.
- Understand the significance of the constant rate in different contexts.
- Apply the knowledge gained to real-life situations that require linear problem-solving skills.
Understanding Proportional Relationships in Math
In mathematics, certain situations arise where two quantities are connected in such a way that when one changes, the other changes in a consistent manner. These types of problems are fundamental to understanding how numbers work together and are crucial in various mathematical fields. Recognizing these patterns allows for easier problem-solving and prediction of outcomes.
One of the key aspects to focus on is how the value of one number affects the other, based on a consistent factor. This factor remains unchanged, which makes it possible to predict future values when one variable is known. In practical terms, this means that if you know how much one quantity increases, you can calculate how much the other quantity will increase or decrease in the same manner.
- The concept of constant change, where two quantities always scale together.
- The ability to identify how one quantity increases or decreases in relation to another.
- The significance of the constant multiplier that links these two quantities.
By understanding these basic principles, you can apply the same logic to solve a wide variety of problems in both theoretical and real-world contexts. Mastery of these ideas is not only important for solving equations but also for interpreting graphs and charts that display these connections.
- Examine how simple equations can illustrate these connections.
- Learn to identify the patterns that occur in graphs and tables.
- Apply your knowledge to real-world examples to see how these mathematical principles play out in everyday situations.
What is the Concept of Slope?
The concept of change is central to understanding how two quantities interact in many mathematical problems. When one value increases or decreases, the rate at which the other value responds is an important factor to consider. This rate, which indicates how steep or gradual the change is, plays a crucial role in analyzing and solving various types of problems.
Understanding the Rate of Change
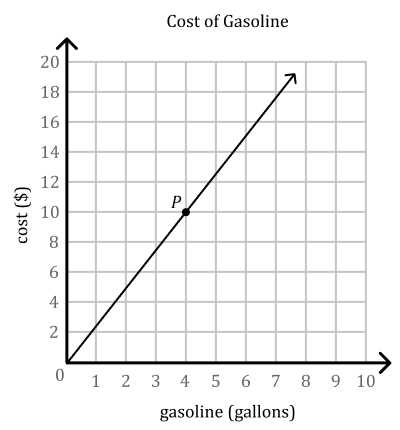
In simple terms, this rate tells us how much one quantity will change for each unit of change in another quantity. It represents the “steepness” or “incline” of a line on a graph, showing how one value increases or decreases in relation to the other. For example, if you’re dealing with a situation where one quantity increases by a certain amount, the rate of change tells you exactly how much the other will increase, based on a fixed relationship.
Interpreting the Graphical Representation
On a graph, this rate is represented as the angle or tilt of a line, where a steep line shows a high rate of change, and a flatter line indicates a lower rate. By examining the graph, you can quickly determine how two values are connected, whether they are rising, falling, or staying constant. This visual representation is an essential tool for understanding and working with problems that involve changing quantities.
How to Identify Proportional Relationships
Recognizing when two quantities are linked in such a way that their values change in a consistent manner is an important skill in mathematics. Identifying this type of connection allows you to predict one quantity when the other is known, based on a fixed ratio or multiplier. Understanding the signs of this relationship can help you solve a variety of problems efficiently.
Key Indicators of Consistent Change
One of the main signs of a consistent connection is when the ratio between two quantities remains constant. If, as one quantity increases, the other increases by the same proportion each time, the quantities are said to be connected in a specific way. This is the key to identifying situations where the two values behave in a predictable manner.
Using Tables to Identify Patterns
One effective way to identify these connections is by organizing data into a table and observing the ratios between corresponding values. If the ratio remains constant across all pairs, the quantities are linked in a consistent manner.
| Quantity 1 | Quantity 2 | Ratio (Quantity 1/Quantity 2) |
|---|---|---|
| 2 | 6 | 2/6 = 1/3 |
| 4 | 12 | 4/12 = 1/3 |
| 6 | 18 | 6/18 = 1/3 |
As shown in the table, the ratio between the two quantities remains the same (1/3) across all pairs. This indicates a consistent connection between the quantities, and the pattern can be applied to predict future values.
The Role of Ratios in Proportions
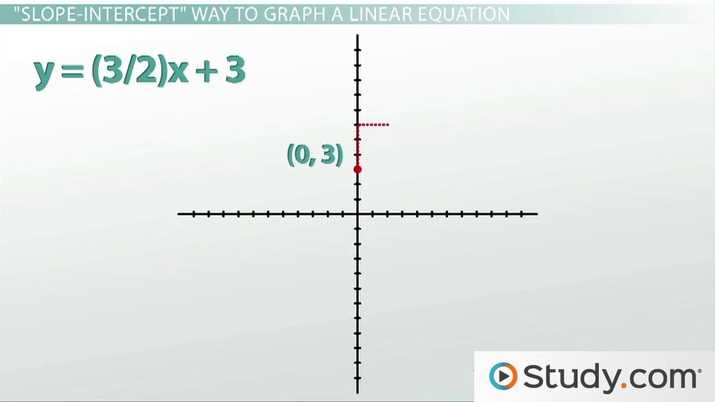
In mathematics, ratios play a fundamental role in understanding how two quantities relate to each other. They are used to express the relationship between these quantities in a way that shows how one changes in comparison to the other. When working with problems involving changing values, recognizing the ratio allows for a clear representation of how one quantity influences the other.
Understanding the Importance of Ratios
Ratios provide a simple yet powerful way to express the relationship between two numbers. When these ratios remain constant across different values, they reveal a consistent pattern that makes it easier to predict future outcomes. By applying ratios, you can understand how one variable affects another in a predictable and measurable way.
- Ratios are used to express the relative sizes of two quantities.
- A constant ratio indicates a fixed relationship between the quantities.
- Understanding ratios allows for easy scaling of values based on the relationship.
How Ratios Work in Real-World Problems
In real-world applications, ratios are often used to solve problems involving scaling, comparisons, or measuring. For instance, they are commonly seen in situations like recipes, speed calculations, or financial analysis, where quantities are compared or scaled to find a solution. Recognizing the role of ratios helps simplify complex situations and makes calculations more manageable.
- Using ratios to adjust quantities in recipes or mixtures.
- Applying ratios to determine speed or efficiency in various contexts.
- Solving financial problems by comparing income and expenses through ratios.
Finding the Slope of a Line
One of the key concepts in understanding the behavior of lines on a graph is determining how steep or flat the line is. This measurement is crucial for interpreting how one variable changes in relation to another. Whether the line rises or falls, this value helps quantify the rate of change, providing valuable insight into the connection between two quantities.
How to Calculate the Rate of Change

To find the steepness, we need to calculate the rate at which one value changes as the other increases or decreases. This can be done by measuring the vertical change between two points on the line and dividing it by the horizontal change. The formula for this calculation is:
Rate of change = (Vertical Change) / (Horizontal Change)
This gives the measure of how much one value changes for each unit change in the other. The result can be positive, negative, or zero, depending on the direction of the line.
Steps to Find the Rate of Change
Follow these simple steps to calculate the rate of change:
- Choose two points on the line. These points should be clearly visible or easy to identify on the graph.
- Find the difference between the y-values (vertical change) and the difference between the x-values (horizontal change) of these two points.
- Divide the vertical change by the horizontal change to get the rate of change.
By following these steps, you can easily determine how rapidly one quantity is changing in relation to another. This calculation is essential for graphing, interpreting trends, and solving a wide variety of real-world problems.
Real-Life Examples of Proportions
The concept of consistent ratios appears in many everyday situations, helping us make sense of the world around us. Whether adjusting a recipe, calculating travel time, or splitting costs, understanding how two quantities scale together allows for efficient problem-solving. These real-life scenarios provide practical applications of mathematical principles, making them essential tools for daily life.
Cooking and Recipe Adjustments
One common example is found in cooking. When you need to adjust a recipe based on the number of servings, you’re essentially working with ratios. If a recipe calls for 2 cups of flour to make 4 servings, you can easily scale it up or down by maintaining the same ratio. For instance, to make 8 servings, you would use 4 cups of flour, keeping the ratio of flour to servings the same.
- Scaling ingredients for larger or smaller portions.
- Adjusting cooking times when changing the quantity of food.
Speed and Travel Time
Another example is calculating travel time based on speed. If you know the distance you need to travel and the speed at which you’re traveling, you can determine how long the trip will take. For example, if you’re driving 60 miles at a speed of 30 miles per hour, it will take 2 hours to reach your destination. The ratio between distance and time remains constant, allowing for easy calculation of travel time at different speeds.
- Determining arrival times based on speed and distance.
- Adjusting routes and time estimates for varying conditions.
These examples demonstrate how ratios and scaling play a vital role in daily tasks, making mathematical concepts accessible and useful in a variety of real-world contexts.
How to Solve Proportional Word Problems
Solving word problems that involve scaling or comparing two quantities requires a systematic approach. These problems often provide a real-world scenario where one quantity changes in relation to another. By identifying the key information and recognizing the relationship between the values, you can easily solve the problem by setting up an equation or using a simple formula.
Step-by-Step Process
The first step in solving these types of problems is to identify the two quantities that are being compared. Once you’ve recognized these quantities, look for any given information about how one quantity changes when the other changes. Then, translate this information into a mathematical expression, usually in the form of a ratio or fraction. Finally, solve for the unknown quantity by applying the appropriate operations.
- Read the problem carefully and identify the two related quantities.
- Write down the ratio or relationship between these quantities.
- Set up an equation based on the given information.
- Solve for the unknown value using arithmetic or algebraic methods.
Example Problem
Let’s consider a simple problem: If 3 apples cost $6, how much do 8 apples cost? Here’s how to solve it:
- First, identify the two quantities: the number of apples and the cost.
- Write the ratio of apples to cost: 3 apples / $6.
- Now, set up the equation: 3 apples / $6 = 8 apples / x (where x is the unknown cost for 8 apples).
- Cross-multiply and solve for x: 3 * x = 6 * 8, so x = 16.
Therefore, 8 apples cost $16. By recognizing the relationship and applying a simple equation, we can easily solve the problem.
Understanding the Slope Formula
The formula to calculate the steepness of a line is an essential concept for analyzing how one variable changes in relation to another. This mathematical tool helps quantify the rate of change between two points on a graph. By understanding how to use this formula, you can accurately describe the direction and steepness of any straight line, whether it’s rising, falling, or horizontal.
The Formula Breakdown
The formula to determine the rate of change is simple but powerful. It is written as:
Rate of change = (Vertical Change) / (Horizontal Change)
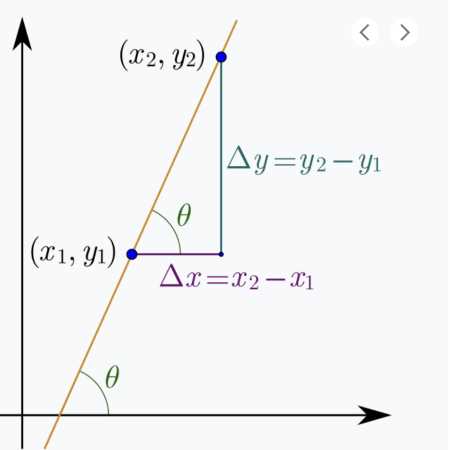
This formula can also be expressed using the coordinates of two points on the line. If you have two points, (x₁, y₁) and (x₂, y₂), the formula becomes:
m = (y₂ – y₁) / (x₂ – x₁)
Here, m represents the rate of change or the steepness of the line, while the differences between the y-values and x-values represent how much the vertical and horizontal positions change between the two points.
Applying the Formula
To use the formula, follow these steps:
- Identify two points on the line. These points should have clear x and y coordinates.
- Subtract the y-coordinates to find the vertical change.
- Subtract the x-coordinates to find the horizontal change.
- Divide the vertical change by the horizontal change to find the rate of change (m).
By following these steps, you can determine how steep the line is and understand how one variable changes in relation to the other. This is crucial for analyzing trends, interpreting data, and solving many types of mathematical problems.
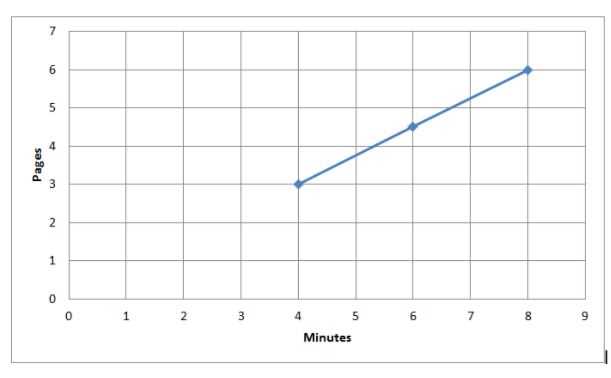
Graphing Proportional Relationships
Graphing two quantities that are linked by a consistent rate of change is a fundamental skill in mathematics. This type of graph shows how one value changes in relation to another in a clear, visual manner. By plotting data points on a coordinate plane and drawing a line through them, you can represent how the two variables scale together. This graphical approach provides insight into the nature of the connection, whether it’s increasing, decreasing, or remaining constant.
When graphing, the key is to identify pairs of values that share a fixed ratio. Each point on the graph represents one pair of values, with the x-axis typically representing the independent variable and the y-axis representing the dependent variable. If the connection between the two variables follows a consistent pattern, the points will align to form a straight line.
To plot these relationships accurately, follow these steps:
- Choose a set of data points that reflect the relationship between the two variables.
- Label the x-axis and y-axis appropriately based on the variables you’re working with.
- Plot each point on the graph according to its x and y values.
- Connect the points with a straight line if they follow a consistent trend.
As a result, you will have a graph that visually displays the connection between the two quantities, making it easier to understand the underlying pattern. Whether analyzing business trends, scientific data, or everyday measurements, graphing is a powerful tool for seeing the bigger picture.
Interpreting the Slope of a Graph
Understanding the rate of change in a graph is crucial for analyzing how two variables are connected. The steepness of the line gives you valuable information about how quickly one value increases or decreases in relation to the other. By interpreting the incline or decline of the line, you can deduce important characteristics of the relationship between the variables, such as whether the trend is increasing or decreasing and by what magnitude.
When analyzing a graph, the rate of change is represented by the angle of the line. A steeper line indicates a larger change in the dependent variable for each unit change in the independent variable. Conversely, a flatter line shows a smaller rate of change.
Key Insights from the Line’s Slope
- Positive Slope: If the line rises from left to right, the relationship is increasing. As one variable increases, so does the other.
- Negative Slope: If the line falls from left to right, the relationship is decreasing. As one variable increases, the other decreases.
- Zero Slope: A horizontal line indicates that there is no change in the dependent variable as the independent variable increases. The two quantities are constant.
- Undefined Slope: A vertical line means that the independent variable does not change, regardless of the dependent variable. This often represents a fixed value.
How to Interpret the Value of the Slope
The exact value of the rate of change can be calculated by measuring the vertical change (the difference in the y-values) over the horizontal change (the difference in the x-values) between two points on the line. This ratio will give you a clear picture of how fast one variable is changing in relation to the other.
By carefully analyzing the graph’s slope, you gain insight into the nature of the connection, which can be applied in various fields, such as economics, physics, and data analysis, to predict behavior and understand trends more effectively.
Common Mistakes with Proportions and Slope
Working with ratios and linear trends can be tricky, especially when interpreting data and applying formulas. Many common errors can occur, which may lead to incorrect conclusions or calculations. Understanding these mistakes can help you avoid pitfalls and improve your mathematical accuracy. Below are some of the most frequent mistakes when dealing with ratios and the rate of change.
Frequent Errors in Calculations
- Incorrectly Identifying Variables: Mixing up the dependent and independent variables is a common mistake. It’s crucial to clearly identify which variable is being changed and which one is responding.
- Forgetting to Simplify Ratios: Ratios should be simplified to their lowest terms. Failure to do this can lead to confusion and errors in further calculations or graphing.
- Misunderstanding the Unit Rate: When calculating the rate of change, it’s important to understand the units involved. Sometimes, the wrong units can be used, or the unit rate may be misinterpreted.
- Improper Use of Formula: Applying the wrong formula for calculating the rate of change or incorrectly using the slope formula can result in inaccurate answers.
Visual Misinterpretations
- Incorrect Graph Scaling: Not choosing appropriate scales for the axes can distort the graph, making it harder to identify trends or calculate the rate of change accurately.
- Assuming a Linear Relationship: Not all data sets follow a straight line. Assuming that the data will always create a straight line can lead to misinterpretation.
- Ignoring Data Points: Sometimes, a small number of outliers may be ignored or misjudged. These points can significantly affect the accuracy of calculations and conclusions drawn from the graph.
How to Avoid These Mistakes
Paying close attention to the details is key to avoiding these common mistakes. Double-check the definitions of variables, simplify ratios, and carefully apply formulas. It’s also essential to carefully graph your data, ensuring that the axes are scaled appropriately and that outliers are taken into account. With practice, these errors can be minimized, leading to better understanding and application of mathematical concepts.
| Common Mistake | Consequence | Solution |
|---|---|---|
| Incorrectly identifying variables | Leads to wrong calculations or interpretations | Clearly define dependent and independent variables |
| Not simplifying ratios | Leads to complex or unclear solutions | Always reduce ratios to their simplest form |
| Misapplying formulas | Results in incorrect outcomes | Review the correct formulas before applying them |
Using Cross Multiplication for Proportions

Cross multiplication is a powerful method for solving equations involving two ratios. This technique allows for quick simplification and provides a clear path to find missing values when two quantities are related. Whether you’re solving for an unknown term or confirming the equality of two ratios, cross multiplication is an essential tool in mathematics.
How Cross Multiplication Works
The process involves multiplying the numerator of one ratio by the denominator of the other ratio. This results in two products that can be compared to solve for the unknown value. Below is a step-by-step guide on how to apply this technique:
- Step 1: Write the two ratios as fractions.
- Step 2: Multiply the numerator of the first fraction by the denominator of the second fraction, and do the same with the other two terms.
- Step 3: Set the two products equal to each other.
- Step 4: Solve the resulting equation to find the unknown variable.
Example of Cross Multiplication
Consider the following equation:
3/4 = x/8
To solve for x using cross multiplication, follow these steps:
- Multiply 3 by 8 (3 * 8 = 24).
- Multiply 4 by x (4 * x = 4x).
- Set the products equal to each other: 24 = 4x.
- Finally, divide both sides by 4 to solve for x: x = 24/4 = 6.
The value of x is 6, showing that cross multiplication provides a straightforward method for solving equations involving ratios.
Benefits of Cross Multiplication
- Efficiency: Cross multiplication simplifies the process of solving for unknowns, especially in complex equations.
- Clarity: This method removes the need for trial and error, making calculations more direct.
- Wide Applicability: Cross multiplication works for many types of ratio problems, making it versatile across different contexts in mathematics.
By mastering cross multiplication, you can quickly and accurately solve many problems involving ratios and unknowns. Whether you’re working with fractions, percentages, or other related concepts, this technique is an invaluable part of any math toolkit.
How Slope Affects Line Steepness
The steepness of a line is a fundamental concept in geometry and graphing. It describes how much the line rises or falls as you move along the x-axis. This characteristic is determined by the ratio of vertical change to horizontal change, which ultimately defines the incline or decline of the line. The greater the value of this ratio, the steeper the line becomes.
In simple terms, when the line’s incline is steep, the change in the y-direction is larger compared to the x-direction, resulting in a line that rises or falls sharply. On the other hand, a gentle incline means that for each unit of horizontal movement, the vertical change is smaller. Understanding this concept is crucial for interpreting graphs, predicting trends, and analyzing real-world data.
The steepness of a line can be adjusted based on the value of the ratio. A higher ratio means a steeper incline, while a lower ratio results in a flatter line. For example, a ratio of 2 would indicate that the line rises by 2 units for every 1 unit it moves horizontally, resulting in a relatively steep line. Conversely, a ratio of 0.5 would show a much gentler slope, as the line rises by only half a unit for each horizontal unit.
These variations in steepness are important when analyzing graphs in fields like physics, economics, or engineering, where understanding the rate of change is key to making predictions and solving problems. The steeper the line, the faster the change is occurring in one direction, which can have significant implications depending on the context of the data.
Proportions and Their Applications in Geometry
In geometry, the concept of ratios plays a critical role in solving problems related to shapes, angles, and dimensions. These relationships are essential for comparing different parts of a figure and understanding how they scale relative to each other. Whether dealing with similar shapes, calculating distances, or analyzing areas, the ability to apply these ratios allows for accurate measurements and solutions.
One of the primary applications of ratios in geometry is in similar figures. When two shapes are similar, their corresponding sides are proportional, meaning the ratio of one side to another is constant across the figure. This principle allows for the calculation of unknown side lengths when the lengths of other sides are known, or when scaling an object while maintaining its proportions.
Another key use of ratios in geometry is in the calculation of areas and volumes. For example, the area of a shape may be proportional to the square of its dimensions, while volume might relate to the cube of the dimensions. These proportional relationships help in scaling objects up or down without losing their geometric properties.
In addition to measuring and scaling, proportions also come into play when working with angles. For instance, understanding the relationship between the sides of a right triangle, known as trigonometric ratios, allows for the calculation of unknown angles or sides based on given information. This application is widely used in fields like architecture, engineering, and navigation.
Key Strategies for Solving Slope Problems
When approaching problems that involve the steepness or incline of a line, several strategies can help break down the process into manageable steps. Whether you are calculating the gradient between two points or analyzing the behavior of a line in a graph, understanding the core principles can lead to more accurate solutions. These methods are essential for determining how a line rises or falls, providing insights into both geometric and algebraic contexts.
One of the most common approaches is the use of the basic formula, which involves taking the difference in vertical values (rise) and dividing it by the difference in horizontal values (run) between two points. This simple calculation gives you the rate of change between those points, which can be interpreted as the incline or tilt of the line. Ensuring that you correctly identify these two points on the graph is key to accurate results.
Another useful strategy is graphing the line first to visually assess its direction and steepness. By plotting points, you can quickly identify trends, whether the line rises steeply, falls gently, or remains horizontal. This visual representation can help check calculations and provide intuitive understanding of the values you’re working with.
For problems involving horizontal or vertical lines, it’s important to recognize that these types of lines have unique characteristics. Horizontal lines have no incline and thus a slope of zero, while vertical lines have an undefined slope due to the lack of horizontal movement. Being aware of these special cases can save time and prevent errors when solving for the rate of change.
Additionally, in problems that require interpreting the context of a real-world situation, such as speed or cost over time, understanding the practical meaning of the line’s incline can be beneficial. The steeper the line, the greater the rate of change, whether it represents an increase in speed, cost, or any other variable. Recognizing these real-life connections can provide further insights and help you apply mathematical knowledge more effectively.
Reviewing Key Concepts in Proportions and Slope
When studying the relationship between two quantities and their changes, it’s essential to revisit the fundamental ideas that govern these connections. Whether analyzing straight lines or comparing two sets of values, recognizing the principles behind the calculations helps build a solid foundation. This review focuses on the core concepts that make up the tools needed to solve these types of problems, ensuring clarity and precision in the application of mathematical reasoning.
Understanding the Rate of Change
The rate of change measures how one quantity changes in relation to another. It is often represented as the steepness of a line on a graph. A key idea to remember is that the steeper the incline, the greater the rate of change. This concept can be applied in various contexts, such as speed, growth, or financial analysis, where it helps quantify how quickly one variable responds to another.
Graphing and Interpretation
Graphing provides a visual representation of the relationship between variables. In many cases, the graphical interpretation of a line reveals important information, such as whether the relationship is increasing, decreasing, or constant. For example, a straight line with a positive incline indicates an increase, while a negative incline shows a decrease. Horizontal lines represent no change, while vertical lines reflect undefined changes.
| Line Type | Interpretation |
|---|---|
| Positive Incline | Increasing relationship |
| Negative Incline | Decreasing relationship |
| Horizontal Line | No change |
| Vertical Line | Undefined change |
By reviewing the core ideas of how changes occur between two variables, whether through numerical methods or graphical representations, it becomes easier to solve problems involving rate of change. Mastery of these concepts leads to a deeper understanding of various mathematical applications and provides a strong foundation for more advanced studies.