
Preparing for a major math test can feel overwhelming, especially when the concepts are complex and the stakes are high. Whether you’re tackling polynomial equations, working with functions, or analyzing graphs, having a clear approach to each problem is crucial for success. This guide provides you with detailed steps, examples, and strategies to help you navigate through the toughest questions you might encounter.
Mastering mathematical techniques requires practice and a solid understanding of the core principles. This resource offers a variety of problems and solutions, breaking down each step to ensure clarity. From solving equations to applying formulas correctly, you’ll gain the confidence needed to excel in the subject.
Through a combination of theory and practical application, this article will guide you in sharpening your problem-solving skills. With each solution carefully explained, you’ll be able to tackle any question with confidence and improve your overall performance. Let’s dive into the essential methods and tools for achieving success in your next assessment.
Final Exam Algebra 2 Answers
When preparing for a comprehensive mathematics assessment, it’s essential to have clear, reliable methods for approaching each question. A strong understanding of the key concepts is crucial for navigating through problems efficiently. This section provides step-by-step solutions to common types of questions you may encounter, helping you grasp the necessary techniques to solve them correctly.
In order to perform well, focus on mastering the following areas:
- Solving systems of equations
- Working with quadratic and polynomial functions
- Understanding rational expressions and equations
- Manipulating exponential and logarithmic functions
- Graphing and analyzing functions accurately
- Applying formulas and solving for unknowns
Each problem is accompanied by a detailed solution, breaking down the process into clear, manageable steps. Here’s a sample approach for solving a quadratic equation:
- Identify the standard form of the equation (ax² + bx + c = 0).
- Apply the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
- Calculate the discriminant (b² – 4ac) to determine the nature of the roots.
- Find the solutions based on the discriminant.
By reviewing problems like these and practicing each type, you will develop a deeper understanding of the material. With consistent preparation and the application of these methods, you’ll be equipped to solve problems accurately and with confidence on your next test.
Understanding the Algebra 2 Exam Format
Knowing the structure of your upcoming math assessment is essential for effective preparation. Familiarity with the types of questions and how they are presented allows you to approach the test with confidence. This section provides an overview of the common formats and sections you can expect, helping you plan your study strategy accordingly.
Typically, these assessments are divided into multiple sections, each focusing on different mathematical concepts. You will encounter a mix of question types, including:
- Multiple-choice questions, where you select the correct answer from a set of options.
- Short-answer problems that require you to show your work and provide a solution.
- Word problems that test your ability to apply mathematical concepts to real-life situations.
- Graphing exercises, where you’ll be asked to plot functions and interpret data.
- Long-form problems, requiring more extensive calculations and reasoning to arrive at the correct solution.
Understanding the types of questions and how they are structured can help you allocate your time wisely. Some sections may require faster problem-solving skills, while others demand more careful, detailed work. Recognizing the format ahead of time will allow you to practice the right techniques and focus on your weak points, giving you the best chance for success.
Key Topics to Review Before the Exam
In order to perform well on your upcoming math assessment, it’s essential to focus your review on the core concepts that are most frequently tested. By honing in on the right topics, you’ll be able to maximize your study time and ensure you’re fully prepared to tackle a wide range of problems. This section highlights the key areas you should prioritize in your preparation.
Equations and Functions
A solid understanding of how to work with different types of equations is fundamental to success. Be sure to review:
- Linear equations and systems of equations
- Quadratic equations and solving methods (factoring, completing the square, quadratic formula)
- Rational expressions and how to simplify and solve them
- Exponential and logarithmic functions, including transformations and applications
Graphing and Analysis
Another critical area is graphing and interpreting functions. Focus on:
- Graphing linear, quadratic, and cubic functions
- Analyzing the behavior of functions (asymptotes, intercepts, domain, range)
- Understanding transformations such as shifts, reflections, and stretches
- Working with systems of inequalities and graphing their solutions
By mastering these key topics, you’ll be well-equipped to approach a wide variety of problems with confidence and clarity, ensuring that you’re fully prepared for the test.
How to Solve Common Algebra 2 Problems
When tackling math problems in higher-level courses, it’s crucial to follow systematic methods that help break down complex questions. By mastering a few key techniques, you can confidently approach a variety of problems and simplify the solution process. This section will provide strategies for solving some of the most common problems you’ll encounter in your studies.
Step-by-step problem solving is essential for accuracy. Always start by identifying the type of problem you’re dealing with and choose the appropriate method. For example, if you’re working with quadratic equations, knowing whether to factor, complete the square, or use the quadratic formula will save you time and effort. Here’s a general approach for solving a quadratic equation:
- Rewrite the equation in standard form: ax² + bx + c = 0.
- Check if factoring is possible. If not, use the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
- Calculate the discriminant (b² – 4ac) to determine the number of real solutions.
- Find the roots based on the discriminant value.
For problems involving functions or graphs, start by plotting key points or identifying intercepts. Knowing how to apply transformations to basic functions will also allow you to graph complex equations with ease. Always double-check your work, especially with word problems, where identifying the correct variables is key to finding the right solution.
With consistent practice and a focus on these common problem-solving methods, you’ll improve your ability to handle a range of challenges and build a strong foundation for more advanced concepts.
Step-by-Step Solutions for Algebra 2 Questions
To master complex math problems, it’s important to break them down into smaller, manageable steps. By following a clear, methodical approach, you can solve even the most challenging questions with confidence. This section will guide you through the process of solving common problems step by step, ensuring you understand each stage of the solution.
Let’s begin with a typical problem involving quadratic equations. Here’s how you can solve it:
- Write the equation in standard form: ax² + bx + c = 0.
- Determine if factoring is possible. If not, proceed with the quadratic formula.
- Apply the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
- Calculate the discriminant (b² – 4ac) to assess the number of real solutions.
- Find the roots based on the discriminant and simplify the equation.
For problems involving functions, follow these steps to graph a quadratic function:
- Identify the vertex of the function by finding h = -b/2a.
- Determine the y-intercept by substituting x = 0 into the equation.
- Plot the vertex and the y-intercept on a coordinate plane.
- Draw the axis of symmetry and sketch the parabola.
By working through problems like these with a clear step-by-step approach, you’ll develop a deeper understanding of the material and enhance your problem-solving skills.
How to Prepare for Algebra 2 Final Exam
Preparing for a major math assessment requires more than just reviewing notes – it involves a structured approach that targets key concepts, strengthens weak areas, and builds problem-solving confidence. Whether you’re revisiting complex equations or mastering graphing techniques, effective preparation will help you approach the test with clarity and precision. This section outlines a strategy to help you get ready and ensure you’re fully equipped to perform at your best.
Start early by identifying the topics that are most likely to appear and that you find challenging. Make a study schedule that breaks down your review into manageable chunks, allowing ample time for each topic. For example, dedicate one session to working through quadratic equations, another to rational expressions, and a third to graphing functions. This approach will help reinforce your understanding and give you time to review any material you’re less familiar with.
Practice regularly with a variety of problems. Start with easier questions to build confidence and gradually move on to more difficult problems. Be sure to practice under timed conditions to simulate the test environment. This will help you manage your time effectively when you’re facing the actual assessment.
Finally, review any past assignments, quizzes, and tests. These are excellent resources for understanding the types of questions that have been asked before and the format you can expect. Don’t hesitate to seek help from your teacher or peers if certain concepts remain unclear. With consistent effort and a focused study plan, you’ll be ready to tackle the test confidently and successfully.
Mastering Quadratic Equations in Algebra 2
Quadratic equations are a fundamental concept in advanced mathematics, and mastering them is essential for success in any related course. These equations, typically in the form of ax² + bx + c = 0, appear frequently on assessments and are key to understanding more complex topics. This section will guide you through different methods for solving quadratic equations, providing clear explanations and examples to reinforce your understanding.
Methods for Solving Quadratic Equations
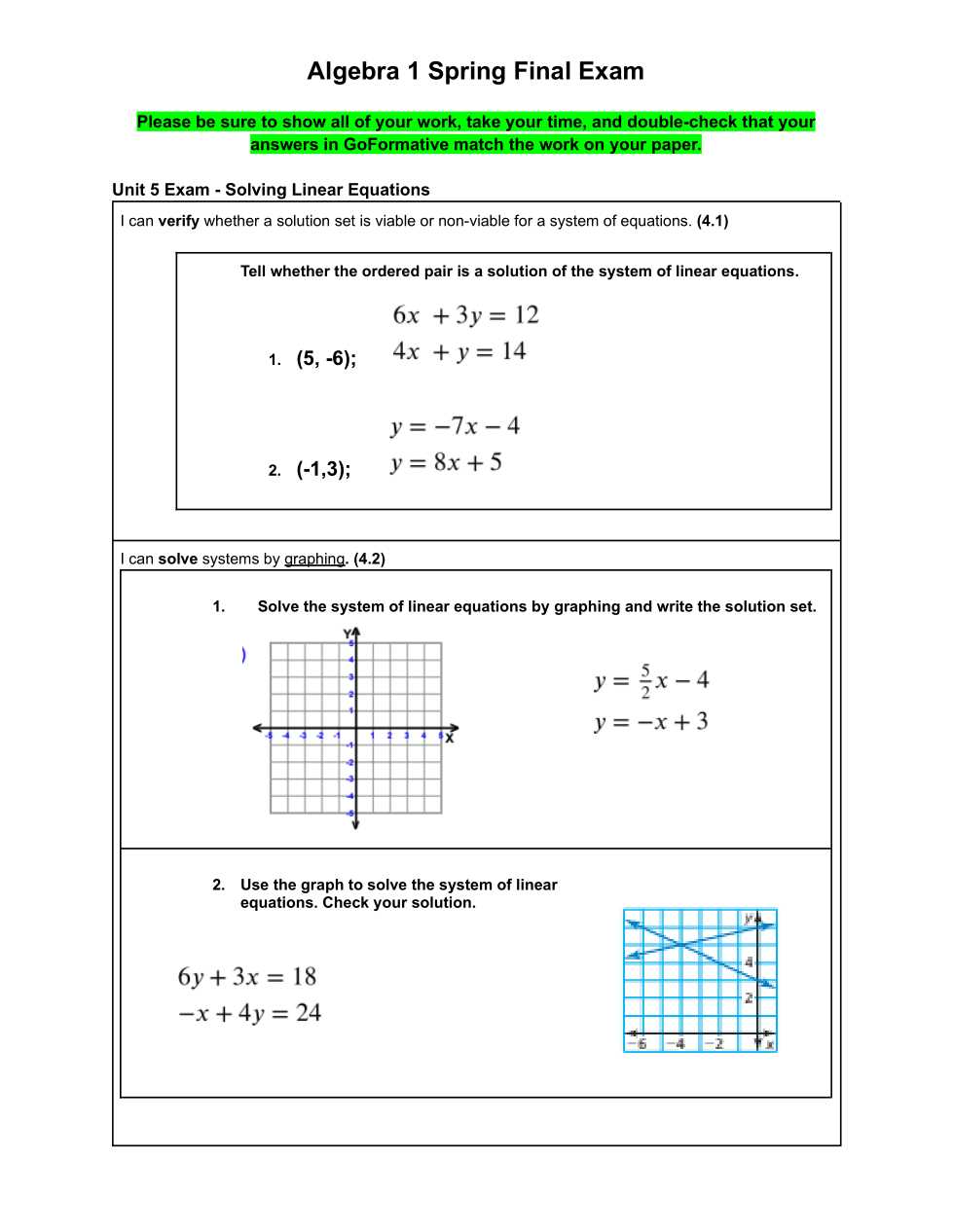
There are several ways to solve quadratic equations, each suited to different types of problems. The most common methods are:
- Factoring: If the quadratic equation can be factored, this is often the quickest and simplest method. Look for two numbers that multiply to give ac and add to give b. Once factored, solve for the variable by setting each factor equal to zero.
- Quadratic Formula: When factoring is not possible, the quadratic formula can be used: x = (-b ± √(b² – 4ac)) / 2a. This formula works for all quadratic equations and provides the roots directly.
- Completing the Square: This method involves manipulating the equation to form a perfect square trinomial, which can then be solved easily. This technique is particularly useful for equations where the quadratic formula may be less intuitive.
Understanding the Discriminant
The discriminant, found inside the square root of the quadratic formula (b² – 4ac), plays a crucial role in determining the nature of the roots. Here’s how it works:
- If b² – 4ac > 0, there are two distinct real solutions.
- If b² – 4ac = 0, there is exactly one real solution (a repeated root).
- If b² – 4ac , there are no real solutions, but two complex (imaginary) solutions.
By practicing these methods and understanding the role of the discriminant, you’ll become proficient in solving quadratic equations and gain confidence in handling a wide range of problems.
Tips for Solving Polynomial Problems
Polynomials are a crucial part of higher-level mathematics, and solving polynomial equations or expressions requires a strategic approach. Whether you’re factoring, simplifying, or finding roots, mastering a few essential techniques can make these problems much more manageable. This section will provide you with effective tips and methods to tackle polynomial problems with confidence and precision.
Factoring Polynomials
One of the most important skills when dealing with polynomials is factoring. Factoring allows you to break down a complex expression into simpler parts, making it easier to solve. Here are some tips for factoring polynomials:
- Look for the Greatest Common Factor (GCF): Before proceeding with any other method, always check if there is a common factor in all terms that can be factored out.
- Use Special Formulas: Familiarize yourself with common patterns such as difference of squares (a² – b² = (a + b)(a – b)) and perfect square trinomials (a² + 2ab + b² = (a + b)²).
- Trial and Error for Trinomials: When factoring quadratics or other higher-degree polynomials, look for two numbers that multiply to give the constant term and add up to the middle coefficient.
Solving Polynomial Equations
Once you have factored a polynomial, solving the equation becomes straightforward. Here are some essential steps for solving polynomial equations:
- Set Each Factor Equal to Zero: If you have factored the polynomial, set each factor equal to zero and solve for the variable.
- Check for Multiple Solutions: Higher-degree polynomials may have multiple solutions. Ensure you check for all possible roots, including real and complex ones.
- Use Synthetic or Long Division: For higher-degree polynomials that don’t factor easily, use synthetic division or long division to break the polynomial into simpler factors.
By practicing these strategies and applying them consistently, you’ll find that polynomial problems become much easier to solve. With a clear understanding of factoring, solving, and simplifying, you’ll be well-prepared to handle any polynomial-related challenge that comes your way.
Understanding Rational Expressions and Equations
Rational expressions and equations involve ratios of polynomials, and working with them requires a solid understanding of how to manipulate fractions with variable terms. These types of problems often appear in various forms, from simplifying expressions to solving equations. Mastering the rules and techniques for dealing with rational functions will help you handle a wide range of questions efficiently.
Simplifying Rational Expressions
The first step in working with rational expressions is simplifying them. To simplify a rational expression, follow these key steps:
- Factor both the numerator and denominator: Look for common factors and factor them out as much as possible.
- Cancel common terms: If there are any common factors in both the numerator and the denominator, they can be canceled out.
- Check for restrictions: Remember that the denominator cannot equal zero. Always identify the values of the variable that make the denominator zero and exclude them from the solution set.
For example, for the rational expression (x² – 9) / (x² – 6x + 9), factor both the numerator and denominator:
- Factor the numerator: x² – 9 = (x + 3)(x – 3).
- Factor the denominator: x² – 6x + 9 = (x – 3)(x – 3).
- Cancel the common factor: (x – 3).
Solving Rational Equations
Rational equations are equations where the variable appears in the numerator or denominator of one or more fractions. To solve rational equations, follow these steps:
- Find the least common denominator (LCD): To eliminate fractions, multiply both sides of the equation by the LCD of all the denominators.
- Simplify the equation: After multiplying by the LCD, simplify the equation to remove the denominators and solve for the variable.
- Check for extraneous solutions: When solving rational equations, always check if any solution makes the denominator zero, as this would not be valid.
For example, to solve 1 / (x – 2) = 3 / (x + 1), multiply both sides by the LCD, which in this case is (x – 2)(x + 1), and solve the resulting equation.
By practicing these steps and becoming familiar with the techniques for simplifying and solving rational expressions, you’ll be able to approach these problems with ease and accuracy, ensuring success in handling them on any assessment.
Tips for Graphing Functions on the Exam
Graphing functions is a crucial skill in many math assessments, and being able to quickly and accurately plot them can make a significant difference in your performance. Understanding how to interpret equations and apply transformations allows you to graph even complex functions with ease. This section provides helpful tips and strategies to improve your graphing skills for various types of functions.
Understanding the Basics of Graphing
Before diving into specific types of functions, make sure you understand the basic principles of graphing:
- Identify key components: Recognize the general form of the function. For example, y = mx + b represents a linear function, and y = ax² + bx + c represents a quadratic function.
- Find the intercepts: Always calculate the x- and y-intercepts, as they provide essential points for plotting the graph.
- Plot key points: Choose specific values for x and calculate the corresponding y values. Plot these points and connect them smoothly.
Graphing Specific Functions
Different types of functions require unique approaches when graphing. Below are some tips for specific types of functions you might encounter:
- Linear Functions: For equations in the form y = mx + b, plot the y-intercept b, then use the slope m to find another point and draw a straight line.
- Quadratic Functions: For equations like y = ax² + bx + c, identify the vertex and axis of symmetry. Then, plot additional points on either side of the vertex and draw a parabola.
- Exponential Functions: For equations like y = a * b^x, start by plotting the y-intercept. Remember that the graph increases or decreases rapidly based on the value of b.
- Rational Functions: Identify vertical and horizontal asymptotes, and plot points near these asymptotes to understand the behavior of the graph.
By following these strategies and practicing regularly, you’ll become proficient at graphing a wide range of functions, which will help you tackle graphing questions with speed and accuracy during any math assessment.
How to Tackle Word Problems in Algebra 2
Word problems can often seem overwhelming, but with a structured approach, you can break them down into manageable parts. The key to solving these types of problems is translating the words into mathematical expressions and equations. Once you identify the right approach, these problems become much easier to handle. This section will guide you through effective strategies for solving word problems in higher-level math courses.
Step-by-Step Approach to Word Problems
To solve word problems efficiently, follow these steps:
- Read the problem carefully: Take your time to understand the scenario. Highlight important numbers, keywords, and any conditions given in the problem.
- Identify what you’re solving for: Focus on the question at the end of the problem. What is the unknown value you need to find?
- Translate the words into an equation: Convert the text into mathematical expressions. Pay attention to relationships such as “total,” “difference,” “product,” and “sum” that indicate operations like addition, subtraction, multiplication, and division.
- Set up the equation: Once you have your expression, solve for the unknown by applying the appropriate mathematical techniques, such as factoring, using the quadratic formula, or solving systems of equations.
Common Strategies for Solving Word Problems
Some word problems require specific methods to find the solution:
- Using systems of equations: If the problem involves two or more unknowns, setting up a system of equations can help you solve for both variables simultaneously.
- Working with rates or proportions: Problems involving speed, distance, or time often require setting up proportions or using rate equations to find the solution.
- Breaking down complex problems: In cases where a problem involves multiple steps, break it down into smaller parts. Solve one part, then use the result to move on to the next step.
By practicing these techniques and approaching each word problem systematically, you’ll improve your ability to tackle even the most complex word problems with confidence and precision.
Common Mistakes to Avoid in Algebra 2
In higher-level math, small errors can quickly snowball into bigger problems, affecting your overall understanding and performance. Recognizing and avoiding these common mistakes will help you improve your accuracy and efficiency. This section highlights some of the most frequent pitfalls that students encounter, along with tips on how to avoid them.
Errors in Simplification and Factoring
One of the most common mistakes is incorrectly simplifying or factoring expressions. When working with polynomials or rational expressions, be sure to:
- Double-check your factoring: Ensure that you’ve fully factored both the numerator and denominator before canceling out common factors. Missing a factor can lead to incorrect answers.
- Pay attention to signs: Watch out for sign errors when simplifying expressions, especially when working with negative numbers. Incorrectly handling signs can drastically change the outcome of your solution.
- Don’t forget the distributive property: When simplifying expressions, remember to distribute terms carefully. Overlooking a distribution can lead to mistakes in both solving equations and factoring.
Misunderstanding Functions and Graphs
Another area where students commonly slip up is in understanding the behavior of functions and graphs. Some key points to remember are:
- Confusing transformations: When applying transformations (shifts, stretches, reflections), always remember the correct order of operations. For example, horizontal shifts are applied before vertical shifts, and stretching occurs after shifts.
- Forgetting asymptotes: When working with rational functions, it’s crucial to recognize vertical and horizontal asymptotes. These features often guide the graphing process, and neglecting them can lead to incorrect graphs.
- Not checking domain and range: Always verify the domain and range of the function you’re working with. Some functions, such as square roots or rational functions, have restrictions that must be accounted for.
Overlooking Details in Word Problems
Word problems can be particularly tricky because they require translating real-world scenarios into mathematical expressions. Common mistakes in word problems include:
- Misinterpreting the question: Always take time to carefully read the problem and determine what you are being asked to find. Many students make the mistake of solving for the wrong variable or misunderstanding the relationship between quantities.
- Ignoring units: Pay attention to the units of measurement in the problem. In many cases, you need to convert units or express the answer in the correct unit of measure.
- Skipping steps: Don’t rush through word problems. Make sure to clearly define variables, set up equations, and solve methodically. Skipping steps can lead to missed details and errors in your final solution.
Avoiding these common mistakes requires practice, attention to detail, and a clear understanding of the concepts involved. By being mindful of these errors, you can significantly improve your problem-solving skills and achieve better results.
Time Management Strategies for the Exam
Effective time management is crucial when preparing for and taking any math assessment. Having a strategy in place allows you to allocate sufficient time to each question, stay calm under pressure, and ensure that you complete the test with time to review your work. This section offers practical techniques to help you manage your time effectively during an assessment.
Pre-Test Preparation
Time management starts long before the test begins. Use the time leading up to the test wisely:
- Create a study schedule: Break down your study material into manageable chunks and allocate specific times for each topic. Make sure to review the most challenging topics first.
- Prioritize weak areas: Identify the areas where you’re weakest and devote extra time to those topics. This ensures you focus your efforts on areas that need the most improvement.
- Practice under timed conditions: Take practice tests or work through problems with a timer to simulate the time pressure of the real test. This will help you develop a sense of how long you should spend on each section.
During the Test
Once the assessment begins, managing your time efficiently becomes even more important. Here are some strategies to use during the test:
- Quickly scan the entire test: At the start of the test, glance through all the questions to get a sense of the difficulty and time requirements. This will help you plan how to tackle them.
- Allocate time for each section: Divide your available time by the number of questions or sections. Make sure to leave time at the end to revisit difficult problems.
- Start with easier questions: Begin with the questions that seem the easiest to you. This will build confidence and allow you to rack up points quickly.
- Don’t get stuck: If you get stuck on a question, move on and come back to it later. Spending too much time on a single problem can jeopardize the rest of your test.
Managing Time for Review
Reviewing your work is an essential step in ensuring you don’t miss any mistakes. Here’s how to make the most of your review time:
- Leave time at the end: Always save at least 10-15 minutes to go over your answers. This gives you a chance to catch any errors or missed questions.
- Check your work systematically: Focus on checking calculations first, then verify your answers to word problems and graphs. Make sure you’ve answered every question.
- Don’t second-guess yourself: Trust your initial answers unless you find an obvious mistake. Overthinking can waste valuable time.
By applying these time management strategies, you can approach the test with confidence, complete the test efficiently, and increase your chances of success. Effective time management isn’t just about speed–it’s about working smart and ensuring you maximize every minute of your test.
How to Use a Calculator During the Test
A calculator can be an invaluable tool during a math assessment, but it’s important to use it wisely and efficiently. Knowing when and how to use the calculator can save you time and help you avoid simple arithmetic errors. This section provides guidance on how to make the most of your calculator during a math test, ensuring you use it as an aid rather than a crutch.
Understand the Calculator’s Functions
Before the test, take the time to familiarize yourself with the features of the calculator you will be using. Key functions to understand include:
- Basic operations: Know how to quickly add, subtract, multiply, and divide, especially for long or complex calculations.
- Advanced functions: Understand how to use functions like square roots, exponents, and trigonometric operations, which may be necessary for higher-level problems.
- Memory functions: Practice storing and recalling values using the memory buttons, which can be useful for saving intermediate results in multi-step calculations.
Use the Calculator Strategically
While a calculator can help you complete many calculations quickly, it’s important not to rely on it for everything. Here are some tips on using the calculator strategically:
- Save time on complex calculations: Use the calculator for lengthy arithmetic or complicated fractions to avoid making errors by hand. This is particularly useful for problems involving large numbers or decimals.
- Double-check your work: After performing a calculation, take a moment to verify that the answer makes sense in the context of the problem before moving on. This will help you catch any potential miscalculations.
- Use estimation when appropriate: Sometimes, a quick estimate can save time and help you check if the calculator’s answer is reasonable. For example, rounding numbers before calculating can give you a rough idea of the expected result.
When Not to Use the Calculator
While a calculator is helpful, there are times when you should not rely on it:
- Simple calculations: For basic math operations that you can easily do in your head or with paper and pencil, avoid using the calculator. This saves time and ensures that you’re still practicing mental math skills.
- When it’s unnecessary: In many cases, test problems are designed to be solved without a calculator. If the problem asks for something simple, like the value of a variable or solving a linear equation, try to solve it manually first.
- During early stages of the test: If you can solve a problem quickly and easily, skip the calculator to avoid wasting time. Focus on using it for more challenging or time-consuming tasks.
By using your calculator thoughtfully and strategically, you can enhance your problem-solving speed while minimizing the chance of errors. It’s an essential tool, but one that should be used with care and consideration throughout the assessment.
Practice Problems for Test Preparation
Practicing a wide variety of problems is one of the most effective ways to prepare for any assessment. By solving different types of questions, you can reinforce your understanding of key concepts, identify areas of weakness, and build your problem-solving speed. In this section, you’ll find several practice problems designed to help you review and prepare for your upcoming assessment. Each problem type focuses on different mathematical skills that are essential for success.
Problem Types to Focus On
Here are some types of problems you should practice to strengthen your skills:
- Equations and Inequalities: Solving linear, quadratic, and rational equations will help you reinforce your understanding of core mathematical principles.
- Functions and Graphing: Be sure to practice working with different types of functions, including exponential, logarithmic, and trigonometric functions, as well as graphing these functions on the coordinate plane.
- Word Problems: These problems often require interpreting real-world scenarios and converting them into mathematical expressions. Practice translating word problems into equations to enhance your skills.
Sample Practice Problems
Use the following problems to practice and improve your mathematical abilities:
| Problem | Solution Method |
|---|---|
| Solve for x: 3x + 5 = 20 | Isolate the variable x by subtracting 5 from both sides and then dividing by 3. |
| Graph the function: f(x) = 2x – 1 | Plot the y-intercept at (0, -1) and use the slope of 2 to plot additional points, then draw the line. |
| Solve for x: (x – 4)(x + 6) = 0 | Set each factor equal to zero and solve for x. |
| Factor the expression: x² – 7x + 10 | Find two numbers that multiply to 10 and add to -7. The factors are (x – 5)(x – 2). |
| Find the value of y when x = 3: y = 4x² – 2x + 1 | Substitute x = 3 into the equation and simplify to find y = 31. |
By practicing these problems and others like them, you can improve your ability to solve various types of questions that are commonly found in assessments. Ensure that you spend time reviewing your solutions, and make sure to identify any areas where you may need further practice. The more you practice, the more confident and prepared you will be.
Reviewing Key Formulas for Success
Mastering mathematical formulas is essential for efficiently solving a wide range of problems. Knowing when and how to apply the correct formula can save time and prevent errors, especially under time constraints. This section highlights some of the most important formulas that you should review in preparation for any assessment. Familiarizing yourself with these formulas and understanding how to use them will help reinforce your problem-solving skills.
Essential Formulas to Remember
The following formulas are frequently used and will be invaluable when tackling various types of problems:
| Formula | Application |
|---|---|
| Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a | Used to find the solutions of a quadratic equation ax² + bx + c = 0. |
| Slope-Intercept Form: y = mx + b | Describes a linear function, where m is the slope and b is the y-intercept. |
| Pythagorean Theorem: a² + b² = c² | Used to find the length of the sides of a right triangle, where a and b are the legs and c is the hypotenuse. |
| Sum of Angles in a Triangle: 180° | States that the sum of the angles in any triangle is always 180°. |
| Distributive Property: a(b + c) = ab + ac | Used to simplify expressions by multiplying each term inside the parentheses by the factor outside. |
Tips for Memorizing Formulas

While knowing the formulas is important, it’s also crucial to remember how and when to apply them. Here are a few tips to help with memorization:
- Practice regularly: The more you work with the formulas, the more familiar they will become. Solve practice problems that require the use of these formulas.
- Create flashcards: Write down the formulas on one side and their applications on the other. Review them regularly to reinforce your memory.
- Understand the logic: Don’t just memorize the formulas–understand why and how they work. This will help you remember them more effectively.
By reviewing these key formulas and practicing their application, you’ll be well-prepared to tackle a wide variety of problems. Make sure to spend time familiarizing yourself with each formula, and understand its application in different contexts. Mastery of these essential formulas is a cornerstone for solving complex problems efficiently.
How to Stay Calm During the Test
Test anxiety can be overwhelming, but staying calm and focused is essential for performing your best. Managing stress effectively during the assessment will help you think more clearly, make fewer mistakes, and approach each question with confidence. In this section, we’ll explore strategies that can help you remain composed throughout the test and maintain a positive mindset.
Practice Relaxation Techniques
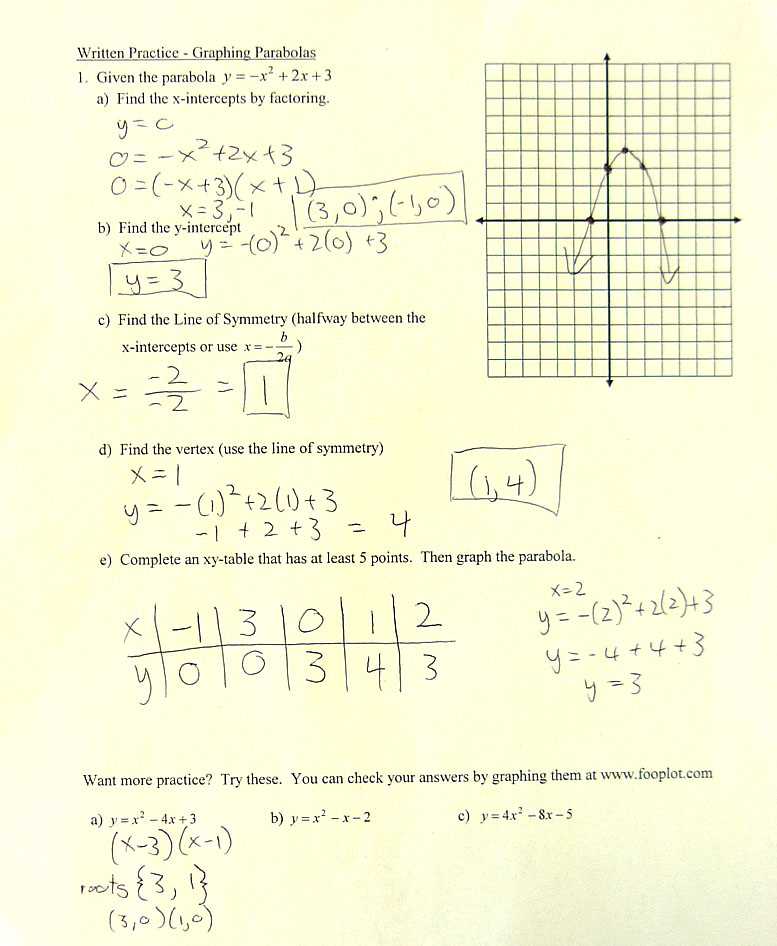
Before and during the test, using relaxation techniques can help calm your nerves and reduce anxiety:
- Deep Breathing: Take slow, deep breaths to calm your mind and body. Inhale for a count of four, hold for four seconds, and exhale for four seconds. This simple technique can help you reset if you begin to feel stressed.
- Positive Visualization: Visualize yourself completing the test confidently and successfully. Imagine yourself solving problems with ease and staying calm. This mental rehearsal can help reduce anxiety and boost your confidence.
- Stretching: Stretching your arms, neck, and shoulders before and during the test can release physical tension and improve focus.
Maintain a Positive Mindset
Your mindset plays a crucial role in managing test-related stress. Staying positive can help you overcome challenges and approach difficult questions with a clear mind:
- Focus on the Present: Don’t dwell on questions you find difficult or worry about how much time is left. Focus on the task at hand and take each problem one step at a time.
- Embrace Mistakes: It’s normal to make errors during a test. Instead of getting frustrated, view mistakes as part of the learning process. Correct them and move forward.
- Stay Organized: Before you begin, take a moment to organize your space, plan how you’ll approach the test, and prioritize easier questions. This can give you a sense of control and reduce stress.
Time Management to Reduce Pressure
Time pressure is one of the biggest sources of stress during an assessment. Managing your time effectively will help you stay calm and avoid rushing through questions:
- Set a Pace: Estimate how long you should spend on each section or problem and stick to it. If a question is taking too long, move on and return to it later if needed.
- Take Breaks: If the test format allows, take brief breaks to stretch, relax, or refocus your mind. A short mental reset can help maintain your energy and clarity.
- Don’t Rush: While time is limited, rushing can lead to careless mistakes. Take your time to understand each question and double-check your answers when possible.
By incorporating these strategies, you can reduce stress and stay focused throughout the assessment. Remaining calm under pressure will not only help you perform better but also boost your confidence for future challenges.