
Mathematical problems often require a clear understanding of underlying principles and methods. This section aims to guide you through various problem-solving strategies, providing you with the tools needed to approach each challenge effectively. By mastering these techniques, you’ll be able to simplify complex tasks and solve equations with confidence.
As you explore this topic, you’ll encounter several key techniques for manipulating expressions, solving systems of equations, and interpreting word problems. Emphasis is placed on logical thinking and step-by-step analysis to ensure that each problem is tackled efficiently. With practice, these skills become essential for mastering more advanced mathematical concepts.
Mathematical Solutions and Techniques
This section explores various methods for solving complex mathematical problems. It covers strategies that help break down equations, tackle challenging word problems, and understand abstract concepts. Mastering these techniques is key to progressing in mathematical learning and building a solid foundation for more advanced studies.
Key Problem-Solving Strategies
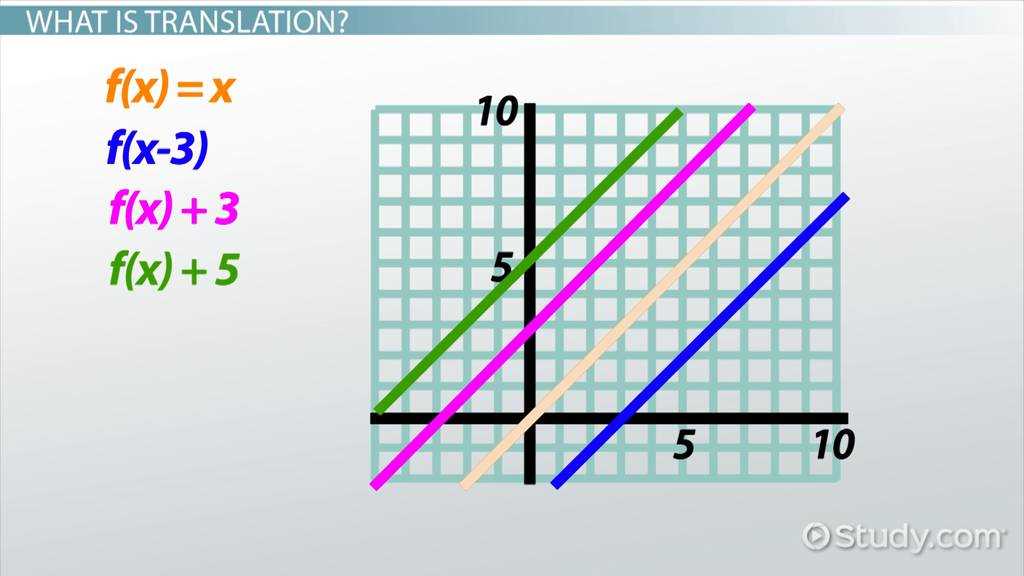
In this part, we focus on essential steps to successfully solve a range of equations. By following a structured approach, you can easily handle even the most intricate tasks. Here are some techniques to keep in mind:
- Start with understanding the problem fully.
- Identify what is being asked and what information is given.
- Apply the appropriate mathematical method or formula.
- Check the solution by substituting it back into the original equation.
Commonly Encountered Problem Types
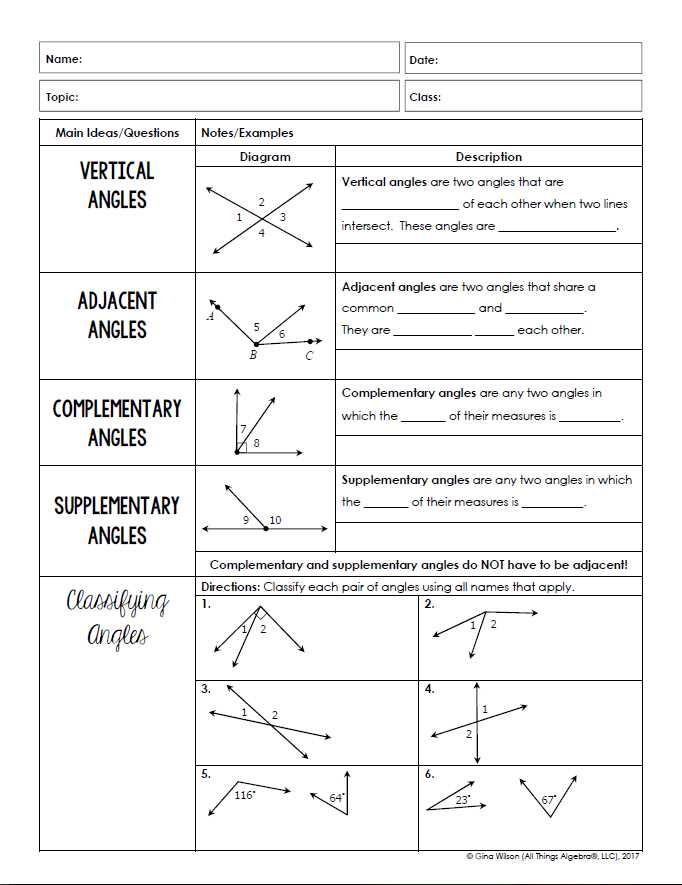
Throughout this section, you will come across different types of problems. Below are some examples of common tasks:
- Solving linear equations with one variable.
- Working with systems of equations and finding their solutions.
- Factoring expressions and simplifying terms.
- Graphing functions and interpreting their slopes and intercepts.
By practicing these methods and familiarizing yourself with common problem types, you’ll be better equipped to approach any mathematical challenge with confidence. Regular practice and review will help reinforce these concepts and improve your problem-solving skills over time.
Understanding Key Concepts in Chapter 7
In this section, we delve into the foundational ideas that are essential for solving a wide variety of mathematical problems. By breaking down the core principles, you will develop a deeper understanding of how different concepts are connected and how to apply them effectively. The key to mastering these topics is not only learning the techniques but also understanding the underlying reasoning that makes them work.
As you progress through these concepts, focus on recognizing patterns, understanding relationships between different elements, and applying logic to solve equations and problems. This approach helps simplify complex tasks and ensures a clearer path toward finding solutions.
| Concept | Description |
|---|---|
| Linear Equations | Understanding the relationship between variables in equations with a single solution. |
| Factoring Expressions | Breaking down expressions into simpler components to make problem-solving easier. |
| Graphing Techniques | Visualizing equations on a graph to identify solutions and trends. |
| Systems of Equations | Solving multiple equations simultaneously to find a common solution. |
Mastering these key concepts will allow you to approach problems from various angles and tackle them with confidence. As you continue practicing, you will gain proficiency and be able to solve more challenging tasks with ease.
Step-by-Step Solutions for Problems
Breaking down complex problems into manageable steps is a critical skill in mathematics. By following a systematic approach, each part of the problem becomes easier to solve. This method not only simplifies the process but also helps ensure accuracy at each stage, ultimately leading to the correct solution.
The process involves carefully analyzing the problem, identifying key elements, and then applying appropriate techniques in a logical sequence. Each step builds on the previous one, leading to a clear understanding of how to approach similar challenges in the future. By practicing this method regularly, you’ll improve both your problem-solving skills and your ability to recognize patterns in different types of problems.
Here’s an example of how to approach a typical problem step by step:
- Read the problem carefully to understand what is being asked.
- Identify the variables and the relationship between them.
- Set up an equation or system of equations based on the given information.
- Perform the necessary operations to simplify or solve the equation.
- Check the solution by substituting it back into the original problem.
By consistently following these steps, you’ll develop a structured approach to solving problems and increase your ability to tackle even more advanced topics with confidence.
Common Mistakes to Avoid in Algebra
When solving mathematical problems, especially those involving equations and expressions, it’s easy to make mistakes that can lead to incorrect solutions. Recognizing and avoiding these common errors is essential for improving your problem-solving skills. Often, these mistakes occur due to misunderstandings of key concepts or rushing through the steps without careful thought.
Common Errors in Operations
Many problems arise from mistakes made during basic operations such as addition, subtraction, multiplication, and division. Some common pitfalls include:
- Incorrectly distributing terms in expressions.
- Forgetting to apply parentheses when necessary.
- Misunderstanding how to handle negative signs, especially when multiplying or dividing by negative numbers.
Overlooking Key Steps in Problem Solving
Other mistakes occur when essential steps are skipped, leading to incomplete or incorrect solutions. These errors can often be avoided by taking your time and reviewing each stage of the solution process:
- Failing to check the solution by substituting it back into the original equation.
- Not simplifying expressions fully before proceeding to the next step.
- Ignoring the context of word problems, which can result in misinterpreting the given information.
By being aware of these common mistakes and taking care to avoid them, you can improve both the accuracy and efficiency of your problem-solving process.
Tips for Mastering Algebraic Expressions
Understanding and manipulating algebraic expressions is a key skill in solving mathematical problems. The ability to simplify, expand, and factor expressions efficiently is crucial for tackling more complex topics. By mastering the basics and following certain strategies, you can improve your proficiency and approach these tasks with confidence.
Essential Techniques for Simplification
Simplifying expressions is often the first step toward solving an equation or problem. Here are some tips to keep in mind when working with expressions:
- Combine like terms whenever possible to reduce the expression to its simplest form.
- Use the distributive property to eliminate parentheses and simplify terms.
- Remember the order of operations (PEMDAS) when simplifying multi-step expressions.
- Factor expressions to find common factors and break them down into simpler components.
Strategies for Expanding and Factoring
Expanding and factoring are critical skills that can help you solve equations more easily. Use the following techniques to work with these types of expressions:
- When expanding, always apply the distributive property carefully to ensure accuracy.
- Factor out the greatest common factor (GCF) from terms to simplify expressions.
- Use special factoring formulas, such as the difference of squares or perfect square trinomials, to identify patterns.
- Check your factoring work by multiplying the factors to ensure they match the original expression.
By practicing these strategies regularly, you’ll develop the skills needed to tackle any expression with ease and accuracy.
How to Solve Linear Equations
Solving linear equations involves finding the value of an unknown variable that satisfies an equation. The process typically requires isolating the variable on one side of the equation by performing a series of mathematical operations. Mastering this technique is essential, as it forms the foundation for solving more complex equations in the future.
To solve linear equations effectively, follow these key steps:
- Step 1: Begin by simplifying both sides of the equation, if needed. This may include combining like terms or distributing values.
- Step 2: Move all terms containing the variable to one side of the equation. You may need to add or subtract terms to achieve this.
- Step 3: Move constant terms to the opposite side by performing the necessary addition or subtraction.
- Step 4: Once the variable is isolated, divide or multiply to solve for its value.
- Step 5: Always check the solution by substituting the value of the variable back into the original equation to verify the result.
By practicing these steps, you’ll become more comfortable with solving linear equations and will be able to approach problems more confidently and efficiently.
Graphing Functions in Chapter 7
Graphing functions is a vital skill for visualizing relationships between variables and understanding their behavior. In this section, we will explore how to represent mathematical expressions as graphs on a coordinate plane. By plotting points and analyzing the resulting graphs, you’ll gain a clearer understanding of how changes in one variable affect the other.
To graph a function, begin by identifying the key components such as the slope, intercepts, and any transformations. Each function has its own characteristics, and learning how to identify these will help you draw accurate graphs. Once you understand the structure of the function, plotting the points becomes a straightforward task.
Here’s a general approach to graphing:
- Identify the function’s key features: slope, y-intercept, and any other transformations (shifts, reflections, etc.).
- Create a table of values by choosing several values for the independent variable (usually x) and calculating the corresponding dependent values (y).
- Plot the points on the coordinate plane.
- Draw the graph, ensuring the line or curve accurately represents the function’s behavior.
- Analyze the graph to understand the function’s key attributes, such as increasing or decreasing intervals, maximum or minimum points, and asymptotes if applicable.
By practicing these steps, you’ll become more confident in graphing various functions and interpreting their graphical representations in different contexts.
Real-World Applications of Algebra
Mathematics plays a crucial role in various aspects of everyday life, and understanding its applications can help you see how important it is beyond the classroom. From managing personal finances to analyzing data, the concepts learned in mathematical problem-solving are essential tools used by professionals in diverse fields. In this section, we explore how mathematical principles, especially those related to solving equations and working with expressions, are applied in real-world situations.
Business and Finance
In business, algebraic methods are commonly used for budgeting, forecasting, and analyzing trends. For instance, businesses use equations to model costs and profits, helping to predict future revenue based on certain factors such as sales, prices, or production levels. Similarly, individuals apply algebra to calculate loans, interest rates, and savings over time, making these skills highly valuable in financial planning.
Engineering and Technology
Engineers and technologists frequently use algebraic techniques to solve problems related to design, construction, and innovation. Whether it’s calculating dimensions for structures or determining the optimal conditions for machinery, algebra helps to solve equations that are vital in fields like electrical engineering, civil engineering, and computer science. Algorithms that drive technology, such as those used in software development and data analysis, also rely heavily on algebraic concepts.
By understanding these applications, you can appreciate the relevance of algebra in everyday life and various industries, making it easier to grasp its importance in solving both practical and theoretical problems.
Analyzing Word Problems Effectively
Word problems are a common challenge in mathematics, requiring not only problem-solving skills but also the ability to translate real-world situations into mathematical expressions. The key to solving these problems lies in understanding the language used, identifying the relevant information, and organizing the steps required to reach a solution. In this section, we will discuss strategies for breaking down word problems and finding the right approach to solve them.
Breaking Down the Problem
The first step in solving a word problem is to read the problem carefully and identify the important details. Focus on the key numbers, operations, and relationships described in the text. Once you’ve gathered the necessary information, restate the problem in your own words, which can help clarify what is being asked and the steps needed to find a solution.
- Identify the unknowns: What are you trying to find?
- Look for important numbers or phrases that indicate operations (e.g., “total,” “difference,” “product”).
- Determine the relationships between the different elements of the problem.
Creating an Equation
After understanding the problem, the next step is to translate the situation into a mathematical equation. This can often involve setting up variables to represent unknown quantities and then using algebraic operations to express relationships. For example, if the problem involves the total cost of items purchased, you might set up an equation involving the price per item and the quantity purchased.
- Define variables to represent the unknown values.
- Use appropriate operations to connect the variables, based on the problem’s language.
- Double-check the equation to ensure it accurately reflects the problem’s conditions.
By following these steps and practicing regularly, you can improve your ability to solve word problems effectively, turning complex scenarios into manageable equations.
Using the Distributive Property

The distributive property is a powerful tool in mathematics that allows you to simplify expressions by distributing a number across terms in parentheses. This property is particularly useful when working with multiplication and addition or subtraction. By applying this rule, you can break down complex expressions into smaller, more manageable parts, making problem-solving easier and faster.
To use the distributive property effectively, follow these basic steps:
- Step 1: Identify the number outside the parentheses and the terms inside the parentheses that need to be multiplied.
- Step 2: Multiply the outside number by each term inside the parentheses.
- Step 3: Simplify the resulting expression by combining like terms, if applicable.
For example, in the expression 3(x + 4), you would distribute the 3 to both x and 4, resulting in 3x + 12. This method can be applied to more complex expressions, whether they involve variables, constants, or both.
Mastering the distributive property helps you handle more complex mathematical problems with ease and lays the foundation for solving equations and simplifying expressions in advanced topics.
Solving Systems of Equations
Solving systems of equations involves finding the values of variables that satisfy multiple equations at once. These systems can appear in a variety of forms, from two-variable equations to more complex ones involving several unknowns. The goal is to find a solution where all equations in the system are true simultaneously, which can be done using different methods, such as substitution, elimination, or graphing.
One of the most common methods for solving systems of equations is the substitution method. This technique involves solving one of the equations for one variable and then substituting that expression into the other equation. This reduces the system to a single equation with one unknown, making it easier to solve.
Another popular approach is the elimination method. In this method, you add or subtract the equations in such a way that one of the variables is eliminated. This leaves a simpler equation that can be solved for the remaining variable. Once that variable is found, you can substitute it back into one of the original equations to find the other variable.
Graphing is also a visual method for solving systems of equations. By plotting both equations on a coordinate plane, the solution is the point where the two lines intersect. While this method can provide a quick solution for some systems, it is often more useful for approximating solutions when working with more complex or non-linear systems.
Mastering these methods allows you to solve systems of equations efficiently and is essential for tackling a wide range of mathematical problems in various fields.
Factoring Techniques Explained
Factoring is a fundamental concept in mathematics that involves breaking down complex expressions into simpler components. This process is often used to solve equations, simplify expressions, and analyze polynomial functions. Mastering factoring techniques is essential for solving quadratic equations and higher-degree polynomials. There are several methods to factor expressions effectively, depending on the structure and type of terms involved.
Factoring by Grouping
Factoring by grouping is a method used when an expression contains four terms. The idea is to group terms in pairs and factor out the greatest common factor (GCF) from each group. Once you’ve factored each group, you can often factor out a common binomial factor from both groups.
- Group the terms in pairs.
- Factor out the GCF from each group.
- Factor out the common binomial.
For example, consider the expression ax + ay + bx + by. By grouping (ax + ay) and (bx + by), you can factor out the GCF from each pair and end up with (a + b)(x + y).
Factoring Trinomials
Factoring trinomials is a method commonly used for quadratic expressions of the form ax² + bx + c. The goal is to find two binomials whose product gives the original trinomial. This method involves finding two numbers that multiply to give ac and add to give b.
- Multiply a and c.
- Find two numbers that multiply to ac and add to b.
- Split the middle term using these two numbers.
- Factor by grouping.
For example, for the trinomial x² + 5x + 6, the two numbers that multiply to 6 and add to 5 are 2 and 3. Therefore, the factored form is (x + 2)(x + 3).
By practicing these techniques, you can efficiently factor polynomials and solve complex equations with ease.
Strategies for Improving Problem Solving
Effective problem solving requires both understanding the problem and knowing the best approach to tackle it. Whether you are working with complex equations or word problems, adopting certain strategies can significantly improve your ability to find solutions. These methods not only streamline the process but also help in building a deeper understanding of mathematical concepts.
One of the first strategies is to break down a problem into smaller, more manageable parts. By simplifying a complex problem into smaller steps, you can focus on solving each part individually. This method can help reduce mistakes and increase your confidence in finding the solution.
Another key approach is to visualize the problem. Graphing equations or drawing diagrams can provide a clearer perspective, especially in problems involving geometry or functions. This visual representation allows you to better understand the relationships between variables and can make it easier to identify patterns.
Use of Logical Reasoning
Logical reasoning plays a crucial role in solving problems efficiently. This involves recognizing patterns, making inferences, and applying known formulas or methods. Sometimes, taking a moment to think through the problem logically before jumping into calculations can save time and reduce errors.
| Strategy | Description |
|---|---|
| Break Down the Problem | Divide the problem into smaller steps to make it easier to handle. |
| Visualize the Problem | Use graphs, diagrams, or charts to help clarify complex relationships. |
| Apply Logical Reasoning | Analyze the problem step-by-step, using known patterns and formulas. |
Finally, practice is essential. The more problems you solve, the better your ability to identify the most effective strategies. Over time, you will develop a stronger intuition for which approach to use in various situations. Regular practice ensures that you are not only able to solve problems more efficiently but also more accurately.
How to Check Your Solutions
Verifying your solutions is an essential part of problem-solving. After working through a mathematical problem, it’s important to ensure that your results are correct. This process helps identify mistakes early and ensures that your conclusions are accurate. Checking your work provides confidence in your calculations and can help you spot errors that may have been overlooked during the initial steps.
One effective method for verification is to substitute your solution back into the original equation or expression. If the result holds true, then your solution is likely correct. For example, when solving an equation, you can replace the variable with the value you obtained and check if both sides of the equation are equal. If they match, it confirms the solution’s validity.
Additionally, you can use different methods to check your solution. For example, if you solved a system of equations, you could use substitution or elimination methods to cross-check the results. If the same solution appears with both techniques, it indicates a correct answer. Alternatively, graphing can be a useful tool for visualizing solutions, especially when working with functions or linear equations.
Tips for Effective Solution Checking
- Substitute values: Always substitute your solution back into the original equation to verify its correctness.
- Use alternative methods: Employ different techniques to cross-check your solution for consistency.
- Graph your results: For equations involving variables, graphing can help visually confirm the solution.
By regularly applying these checking techniques, you can improve your accuracy and avoid common mistakes. Remember, thorough verification ensures that you are not just arriving at a solution but arriving at the correct one.
Breaking Down Complex Problems
When faced with complicated problems, breaking them down into smaller, more manageable parts is an effective strategy. Tackling a large issue can feel overwhelming, but by dividing it into simpler tasks, you can focus on one step at a time. This approach not only makes the problem more approachable but also increases the chances of finding a correct solution.
Start by understanding the core components of the problem. Identify the key variables, relationships, and steps involved. Once you have a clear picture, break the problem into smaller chunks. Focus on solving one part before moving on to the next. As you progress, constantly check your work to ensure that each step builds towards the overall solution.
Steps for Breaking Down Problems

- Identify the main variables: Recognize the unknowns and the relationships between them.
- Divide the problem into parts: Split the task into smaller, more manageable segments.
- Work on one part at a time: Solve each part independently before combining them.
- Check your progress: After solving each part, verify its accuracy before moving forward.
Using this approach helps maintain clarity and ensures that nothing is overlooked. By systematically solving smaller components, you can successfully address even the most challenging issues. This strategy not only applies to mathematical problems but can be used for complex tasks in other areas as well.
Practice Exercises for Chapter 7

To master the concepts presented in this section, practicing a variety of problems is essential. The exercises will help reinforce your understanding of the key principles and allow you to apply them to different situations. Regular practice ensures that you become more comfortable with the material, ultimately leading to better retention and problem-solving skills.
Working through exercises allows you to identify areas where you might need more focus. By solving progressively challenging problems, you can track your improvement and develop a deeper understanding of the topics covered. Whether you prefer working through examples step by step or attempting complex problems, consistent practice is crucial for success.
Exercise Examples
- Solve linear equations: Find the value of the unknown by using various methods such as substitution or elimination.
- Factor expressions: Break down expressions into simpler components by applying factoring techniques.
- Graph equations: Plot points on a coordinate plane and understand the relationship between variables.
- Work through word problems: Translate real-world scenarios into mathematical expressions and solve for the unknowns.
Benefits of Regular Practice
- Improves accuracy: Consistent practice helps reduce errors and improves your ability to solve problems quickly.
- Builds confidence: As you become more familiar with the material, you will feel more confident in tackling more difficult questions.
- Enhances problem-solving skills: Regular exercises develop critical thinking and decision-making skills, which are important for solving complex problems.
By dedicating time to practice, you will strengthen your grasp of the material and be better prepared to handle various challenges in this topic.
Preparing for Algebraic Assessments
Success in any mathematical evaluation requires both understanding the concepts and practicing the techniques needed to solve problems. Preparation involves more than just memorizing formulas or procedures; it is about building the confidence and skills necessary to approach a wide variety of problems. A focused study plan and consistent practice can significantly improve performance in these assessments.
To prepare effectively, it is essential to review the main topics covered, identify areas of weakness, and focus on mastering them. Solving practice problems, revisiting challenging concepts, and seeking clarification on any doubts will ensure that you are ready for the test. Additionally, working with sample assessments can help familiarize you with the format and the types of questions that might be asked.
Study Tips
- Review key concepts: Make sure you understand the fundamental principles, such as solving equations, graphing, and simplifying expressions.
- Practice regularly: Consistent practice is essential for solidifying your understanding and improving your problem-solving speed.
- Work on sample problems: Test yourself with different types of problems to become comfortable with a range of scenarios.
- Identify and focus on weaknesses: Pay extra attention to the areas where you struggle most, and spend additional time improving those skills.
- Stay organized: Keep notes and study materials organized for easy review. This will help you quickly find important information during your study sessions.
Mindset for Success
- Stay calm: Approaching the assessment with a clear, focused mind will help you think more critically and avoid unnecessary mistakes.
- Trust your preparation: Confidence in the work you’ve done to prepare will give you the assurance needed to perform well.
- Manage your time: During the assessment, allocate enough time for each problem, and do not spend too long on any one question.
By following these strategies and committing to regular practice, you will be well-prepared to excel in any upcoming assessment.