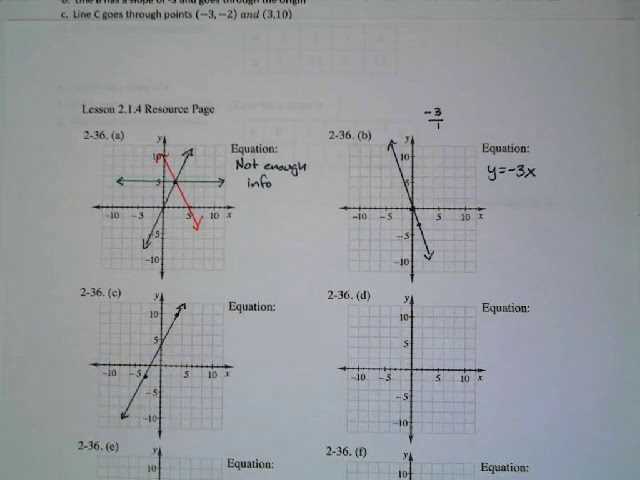
Understanding complex mathematical concepts requires clear strategies and practice. By breaking down difficult tasks and applying logical steps, learners can navigate through challenging problems with confidence. This approach helps in reinforcing essential principles while improving problem-solving skills.
Whether it’s simplifying equations or mastering advanced calculations, having a structured method is key to success. With the right tools and guidance, students can gain a deeper grasp of the material, ensuring they overcome obstacles and excel in their studies. Engagement with the material plays a critical role in long-term mastery, turning theoretical knowledge into practical ability.
Mathematical Problem Solutions
When tackling complex mathematical tasks, having a structured approach to finding solutions is essential. By breaking down each problem into smaller, manageable steps, learners can systematically work through challenges. The key is not just knowing the formula but understanding the reasoning behind it and applying it effectively to different types of questions.
Steps to Solve Mathematical Problems
- Identify the given information and what is being asked.
- Determine the appropriate method or formula for the problem.
- Carefully perform the calculations, checking each step for accuracy.
- Review the final result to ensure it makes sense within the context.
Tips for Mastering Solutions
- Practice regularly to build familiarity with various problem types.
- Use diagrams or graphs to visualize problems, particularly with functions and inequalities.
- Double-check work to avoid common mistakes such as calculation errors or misinterpreting the question.
With consistent practice and applying these strategies, students can gain confidence in solving complex problems, improving both their accuracy and speed. The process becomes more intuitive as familiarity grows, making it easier to approach new and unfamiliar challenges.
Step-by-Step Problem Solving Techniques
Approaching a mathematical challenge requires a clear and systematic method to ensure accuracy and efficiency. Breaking down each task into smaller steps allows for better understanding and reduces the risk of errors. By following a structured process, complex problems become easier to manage and solve.
Effective Problem-Solving Process
- Read the problem carefully and highlight important information.
- Identify what the problem is asking and determine the goal.
- Choose the right strategy or formula to solve the problem.
- Work through the problem step by step, checking each calculation.
- Reassess the final solution to ensure it meets the initial requirements.
Common Approaches to Problem Solving
- Use substitution or elimination for solving equations involving multiple variables.
- Graph functions to visually identify solutions and trends.
- Break word problems into smaller parts and translate them into equations.
- Test solutions by plugging them back into the original problem to verify correctness.
By consistently applying these techniques, students can enhance their problem-solving skills and become more confident in tackling a wide range of mathematical challenges. Each method offers a unique approach depending on the nature of the task, but the core principle remains the same: clarity and methodical execution lead to success.
Understanding Key Mathematical Concepts
Mastering essential mathematical ideas is crucial for solving more complex problems. Gaining a solid understanding of fundamental principles not only helps in tackling specific tasks but also forms the foundation for learning advanced techniques. By focusing on core concepts, students can build confidence and improve their ability to solve various types of mathematical challenges.
Important Concepts to Grasp
- Equations and Inequalities: Understanding how to manipulate and solve different types of equations is essential for progressing in math.
- Functions and Graphs: Learning how functions behave and how to represent them visually is crucial for analyzing relationships between variables.
- Quadratic Relationships: Recognizing the patterns in quadratic equations and knowing how to solve them is key for dealing with more advanced problems.
Techniques for Mastery
- Practice regularly: Reinforce concepts through consistent exercises to enhance understanding and recall.
- Use real-life examples: Apply mathematical ideas to practical situations for better comprehension and relevance.
- Seek help when needed: Don’t hesitate to ask for clarification on difficult concepts to ensure a clear grasp of the material.
By developing a strong foundation in these key areas, students will not only be able to solve specific problems more efficiently but also gain the skills necessary for tackling more advanced topics in mathematics.
Common Mistakes and How to Avoid Them
When working through mathematical tasks, it’s easy to make mistakes that can lead to incorrect solutions. Recognizing these common errors and understanding how to prevent them is essential for improving accuracy and efficiency. By becoming aware of typical pitfalls, students can learn to spot mistakes early and avoid them in the future.
Frequent Errors in Mathematical Tasks
- Misinterpreting the Problem: Failing to clearly understand the question can lead to solving the wrong equation or using the wrong approach.
- Calculation Mistakes: Simple errors in arithmetic or signs can result in incorrect answers. Always double-check your work.
- Forgetting to Apply the Correct Formula: Using the wrong formula or applying it incorrectly is a common issue. Make sure you know which formula to use for each type of problem.
How to Minimize Errors
- Read Carefully: Take the time to fully understand the problem before attempting to solve it. Identify key information and what is being asked.
- Check Your Work: Always review your calculations, especially when solving equations or performing complex operations.
- Practice Regularly: The more problems you solve, the more familiar you become with the techniques and the less likely you are to make errors.
By staying mindful of these common mistakes and taking the necessary precautions, students can significantly improve their problem-solving abilities and avoid unnecessary setbacks.
Effective Strategies for Solving Equations
Solving equations requires a methodical approach to ensure that each step is completed correctly. Whether the equation involves simple arithmetic or more complex variables, following clear strategies helps in reaching the solution efficiently. Understanding the fundamental techniques allows for quicker and more accurate problem-solving.
Key Approaches to Solving Equations
- Isolation of Variables: One of the most effective strategies is isolating the variable on one side of the equation. This simplifies the process and makes it easier to solve.
- Balancing the Equation: Always remember to perform the same operation on both sides of the equation to maintain balance. This ensures the equation remains true throughout the process.
- Using Substitution: For equations involving multiple variables, substitution can be a powerful tool to eliminate variables and simplify the equation to a more solvable form.
Tips for Efficient Solving
- Check for Common Factors: Before diving into more complex operations, check if there are any common factors that can be factored out to make the equation easier to handle.
- Work Step-by-Step: Take the time to carefully work through each step. Rushing through can lead to mistakes, especially in equations with multiple variables.
- Verify Your Solution: Once a solution is found, always substitute the values back into the original equation to ensure they satisfy the equation.
By practicing these strategies and applying them consistently, solving equations becomes a more straightforward process, leading to more accurate and quicker solutions in mathematical tasks.
Tips for Mastering Functions
Functions are a fundamental concept in mathematics, and mastering them is key to solving more complex problems. Understanding the relationship between variables and how one affects the other is crucial for success. By practicing different types of functions and applying various techniques, students can develop a deeper understanding and increase their problem-solving skills.
Understanding the Basics of Functions
To fully grasp functions, it’s important to begin by understanding their definition and how they represent relationships. Here are some important aspects to keep in mind when learning about functions:
| Aspect | Description |
|---|---|
| Domain | The set of all possible input values (independent variable). |
| Range | The set of all possible output values (dependent variable). |
| Function Notation | Using symbols like f(x) to express a function’s output for a given input. |
Techniques for Mastering Functions
- Practice Identifying Functions: Work on recognizing functions from various equations and graphs. This helps in understanding their behavior and properties.
- Use Graphs to Visualize Functions: Visualizing functions graphically helps to see how changes in the input affect the output. Plotting functions allows you to analyze their trends and relationships.
- Familiarize Yourself with Different Types: Understand the different types of functions, such as linear, quadratic, and exponential. Knowing their characteristics and how they differ will help you solve a variety of problems.
With consistent practice and a solid understanding of the core concepts, mastering functions becomes a manageable and rewarding process. By applying these tips and techniques, students can significantly improve their skills and confidence when working with mathematical functions.
Practice Problems for Mastery
To truly master mathematical concepts, it’s essential to practice regularly. Working through various problems allows students to strengthen their skills and gain confidence in solving more complex challenges. The following exercises are designed to reinforce key principles and provide hands-on experience with different types of problems.
Essential Practice Problems
- Solve Linear Equations: Find the value of the variable in simple linear equations.
- Factor Quadratic Expressions: Practice factoring expressions into binomials or other forms.
- Graphing Functions: Plot different types of functions, such as linear, quadratic, and exponential, on a graph.
- Solving Systems of Equations: Use methods like substitution or elimination to find solutions to systems involving two or more equations.
- Working with Exponents: Simplify expressions involving exponents and apply the rules for multiplying and dividing powers.
Challenging Exercises
- Word Problems: Translate real-world situations into mathematical expressions and solve for the unknowns.
- Solving Inequalities: Solve both simple and compound inequalities, and graph the solutions on a number line.
- Polynomial Division: Practice dividing polynomials using long division or synthetic division.
By regularly working through these practice problems, students will develop a stronger grasp of key mathematical concepts and be better prepared for tackling more advanced topics. The more diverse the problems, the better equipped learners will be to approach unfamiliar challenges with confidence.
How to Check Your Solutions
Verifying the correctness of your solutions is an essential part of the problem-solving process. By double-checking your work, you can identify errors, improve your understanding, and build confidence in your ability to solve similar problems in the future. Implementing a few simple strategies can help ensure accuracy and prevent mistakes from going unnoticed.
Start by reviewing each step carefully. Revisit the methods and operations you used to reach your solution, ensuring that every calculation and logical step was executed correctly. Check for any possible misinterpretations of the problem, and ensure the solution aligns with the context or requirements of the question.
Another effective method is to substitute your solution back into the original problem to verify its validity. This helps confirm whether the values you’ve calculated satisfy the equation or meet the given conditions. If the result doesn’t work, it’s a clear sign that an error was made somewhere along the way.
Lastly, using alternative approaches or solving the problem in a different order can help verify your results. This not only strengthens your understanding of the problem but also provides a chance to catch any inconsistencies or missteps.
Learning to Work with Polynomials
Understanding how to manipulate and solve problems involving polynomials is a crucial skill in mathematics. Polynomials are expressions consisting of terms that can be added, subtracted, or multiplied, each involving variables raised to various powers. Mastering the operations on these expressions opens the door to solving complex problems in algebra and beyond.
To work effectively with polynomials, it’s essential to become comfortable with their structure and the operations that can be performed on them. Here are some key techniques and methods for handling polynomials:
- Adding and Subtracting Polynomials: Combine like terms by adding or subtracting their coefficients. Make sure to keep track of the exponents on the variables.
- Multiplying Polynomials: Use the distributive property (also known as the FOIL method) to multiply binomials or higher-degree polynomials.
- Factoring Polynomials: Factor expressions by identifying common factors, applying factoring formulas, or using methods like grouping or synthetic division.
Additionally, being able to identify the degree and the leading coefficient of a polynomial helps in analyzing its behavior, especially when graphing the expression or solving related equations. By practicing these techniques and building a strong foundation, working with polynomials becomes more intuitive and manageable.
Whether simplifying an expression, solving polynomial equations, or performing operations, mastering these steps will enhance your ability to tackle a wide variety of problems involving polynomials.
Graphing Techniques for Mastery

Graphing is an essential skill that allows you to visually interpret mathematical relationships and solve problems effectively. By plotting equations and functions on a coordinate plane, you can identify key features such as intercepts, slopes, and asymptotes. Mastering various graphing techniques helps in understanding the behavior of different types of mathematical expressions and aids in solving complex problems with ease.
Key Graphing Methods

- Plotting Linear Equations: For linear functions, identify the slope and y-intercept to draw a straight line representing the equation. This method is fundamental for visualizing relationships between variables.
- Graphing Quadratics: Quadratic functions are often represented as parabolas. Find the vertex, axis of symmetry, and intercepts to draw an accurate graph of a quadratic equation.
- Graphing Exponentials: Exponential functions have rapid growth or decay. Focus on identifying key points like the y-intercept and the horizontal asymptote to graph these types of equations correctly.
Advanced Graphing Techniques
- Transformations of Functions: Understand how shifts, stretches, and reflections affect the graph of a function. Apply these transformations to sketch functions that have been modified from their standard forms.
- Using Technology: Graphing calculators and software can make graphing more efficient, especially when dealing with complex functions. Learning to use these tools can save time and help check your work.
With consistent practice and a solid understanding of these techniques, graphing will become a valuable tool for solving problems and visualizing mathematical concepts. Whether you’re analyzing linear trends or exploring complex functions, mastering graphing techniques is crucial for mathematical success.
Transforming Word Problems into Equations

Converting word problems into equations is a critical skill in solving real-life mathematical situations. By translating the narrative into a mathematical expression, you can identify the variables, relationships, and unknowns, turning a complex problem into something manageable. This process involves interpreting the language and structure of the problem and applying appropriate mathematical operations to model the situation accurately.
To begin, break down the problem into smaller parts. Identify what is being asked and the given information. Assign variables to unknowns and set up relationships based on the context. Once the equation is formulated, you can apply algebraic methods to solve it.
| Step | Action |
|---|---|
| Step 1 | Read the problem carefully and identify key information. |
| Step 2 | Assign variables to unknown quantities. |
| Step 3 | Translate the relationships and conditions into an equation. |
| Step 4 | Solve the equation using appropriate methods. |
| Step 5 | Interpret the solution in the context of the original problem. |
For example, if a problem involves finding the total cost of items with given prices and quantities, you can express the total as an equation by multiplying the price per item by the quantity, and then adding up the results for each item. This transforms the word problem into an equation that can be solved using simple arithmetic operations.
By practicing this process, you will develop a systematic approach to solving word problems and gain confidence in applying mathematical reasoning to everyday situations.
Solving Systems of Equations Efficiently
Solving multiple equations simultaneously is a key technique in mathematics, often used to find the values of variables that satisfy all given conditions at once. The process involves identifying the points of intersection between equations, where the values of the variables make all equations true. This skill is crucial in both theoretical and practical problem-solving, from business calculations to engineering designs.
There are several methods to solve these systems efficiently, each suited for different types of problems. The most common methods include substitution, elimination, and graphical solutions. Each of these methods has its advantages depending on the complexity of the system and the type of equations involved.
| Method | Description |
|---|---|
| Substitution | One equation is solved for one variable, and the result is substituted into the other equation to simplify the system. |
| Elimination | By adding or subtracting equations, variables are eliminated, making it easier to solve for the remaining variable. |
| Graphical | The equations are graphed, and the solution is the point where the graphs intersect. |
For example, if you are given a system of two linear equations, you can use the substitution method by solving one of the equations for one variable and then substituting that expression into the other equation. Alternatively, with the elimination method, you can multiply one or both equations by factors that allow you to cancel out one of the variables when added or subtracted.
By choosing the most efficient method based on the problem, you can solve systems of equations more quickly and accurately, saving time and reducing complexity.
Utilizing Resources for Math Help

When faced with challenging problems, using available resources can greatly enhance understanding and improve problem-solving skills. Whether you’re stuck on a specific concept or need general guidance, a variety of tools and materials are at your disposal to make learning more efficient. From online platforms to study groups, these resources can provide the support necessary to master difficult topics.
Online Platforms and Tutorials
The internet offers a wealth of platforms dedicated to helping students with mathematical problems. Websites and apps often feature step-by-step tutorials, video explanations, and interactive problem sets. These resources allow students to learn at their own pace, reinforcing concepts they may find difficult. Some platforms even provide personalized assistance, offering tailored explanations and solutions based on your progress and learning style.
Study Groups and Peer Support
Collaborating with classmates or joining a study group is another effective way to approach complex topics. Discussing problems with peers can help you see different approaches to the same question, deepening your understanding. Sometimes, teaching a concept to others can also solidify your own comprehension. Additionally, peers can often explain topics in a way that is more relatable and easier to grasp.
By combining online resources, study groups, and practice, you can steadily improve your skills and approach even the most challenging problems with confidence.
Common Math Challenges Students Face
Many students encounter a range of difficulties when tackling advanced mathematical problems. These challenges can stem from various aspects of problem-solving, from understanding complex concepts to applying the right strategies. Recognizing these common obstacles is the first step toward overcoming them and improving performance. Whether it’s struggling with equations, functions, or graphing techniques, each difficulty can be addressed with the right approach and practice.
Struggling with Complex Equations
One of the most frequent issues students face is solving complex equations. These can involve multiple variables, fractions, or exponents, requiring a deep understanding of different mathematical rules and operations. Breaking down each equation step-by-step and isolating variables can help, but it’s essential to stay organized and avoid rushing through the process.
Difficulty in Visualizing Functions and Graphs
Another common challenge is understanding and graphing functions. Visualizing how different functions behave on a coordinate plane can be overwhelming, especially when dealing with quadratic, exponential, or logarithmic equations. It often helps to draw several examples and look for patterns, as well as practicing with graphing tools to gain a clearer understanding of how the equations relate to their graphical representations.
While these challenges can be frustrating, they are not insurmountable. With the right mindset, tools, and resources, students can develop the skills to tackle even the toughest math problems efficiently and with confidence.
Understanding Quadratic Equations Thoroughly
Quadratic equations are a fundamental part of mathematics, appearing in various real-world applications and advanced mathematical topics. These equations typically involve variables raised to the second power and can be solved in several ways, such as factoring, completing the square, or using the quadratic formula. Mastering these methods is essential for gaining a deeper understanding of how quadratic relationships work and how they can be manipulated to solve problems effectively.
When working with quadratic equations, it’s important to recognize their general form: ax² + bx + c = 0, where a, b, and c are constants. Identifying the coefficients correctly and understanding their impact on the equation’s graph is crucial. The graph of a quadratic equation is a parabola, and by examining the equation’s parameters, you can predict its shape, direction, and key features like the vertex and axis of symmetry.
For students struggling with quadratic equations, understanding the different methods of solving them can greatly improve their problem-solving skills. Practice is key to mastering these equations, so students should be familiar with each approach and when to apply them effectively. Whether solving via factoring, using the quadratic formula, or completing the square, knowing how and when to use these techniques will help simplify complex problems and enhance overall mathematical understanding.
Building Confidence in Algebra 2 Solutions
Building confidence in solving mathematical problems is a crucial aspect of mastering any subject. When it comes to advanced problem-solving, particularly those involving equations, functions, and graphs, feeling comfortable with the material can make a significant difference in performance. Gaining confidence not only helps improve understanding but also makes the process more enjoyable and less intimidating.
One of the most effective ways to build confidence is through consistent practice and exposure to a wide range of problems. By repeatedly solving similar types of equations and gradually increasing the difficulty level, students can reinforce their skills and enhance their problem-solving techniques. Understanding the underlying concepts rather than memorizing formulas helps build a strong foundation for tackling complex problems confidently.
Key Strategies for Building Confidence
- Practice Regularly: Consistent practice helps solidify knowledge and reduces anxiety when facing new problems.
- Start with Simpler Problems: Begin with easier problems and progressively move to more challenging ones to build competence at a comfortable pace.
- Review Mistakes: Understanding errors and learning from them strengthens the problem-solving process and improves accuracy.
- Use Visual Aids: Diagrams and graphs can offer helpful insights, especially when dealing with complex equations and functions.
- Work with Peers: Collaborative problem-solving allows students to share strategies and gain different perspectives on tackling problems.
Tracking Progress
Monitoring your progress is essential to maintaining motivation and ensuring improvement. By tracking how well you solve problems and identifying areas of difficulty, you can focus on specific topics that need further attention. Keeping a record of solved problems and reviewing them periodically can also boost confidence as you see how much progress you’ve made.
| Strategy | Benefits |
|---|---|
| Consistent Practice | Improves familiarity with problem types and reduces anxiety |
| Starting with Simpler Problems | Builds confidence and creates a strong foundation |
| Reviewing Mistakes | Helps avoid repeated errors and reinforces learning |
| Collaborating with Peers | Expands problem-solving techniques and strategies |
By implementing these strategies, students can gradually increase their confidence and tackle even the most challenging problems with ease. Confidence in mathematical problem-solving grows with time and persistence, so don’t hesitate to approach each new problem as an opportunity to strengthen your skills.