Core Connections Algebra 1 Chapter 6 Answers

In this section, we explore important mathematical principles that form the foundation for more advanced topics. Focusing on essential problem-solving techniques, this material provides a thorough understanding of various numerical relationships and how to apply them effectively in different scenarios.

By working through the exercises, you will gain a clearer grasp of how to manipulate variables and solve for unknowns in various mathematical contexts. These skills are crucial for progressing to more complex equations and problems, allowing you to build a strong foundation for further learning.

Understanding the concepts and strategies presented here will empower you to tackle more challenging tasks with confidence. With consistent practice, you will develop the necessary tools to approach and solve problems efficiently and accurately. Success in these exercises lays the groundwork for mastering higher-level topics in mathematics.

Core Connections Algebra 1 Chapter 6 Answers

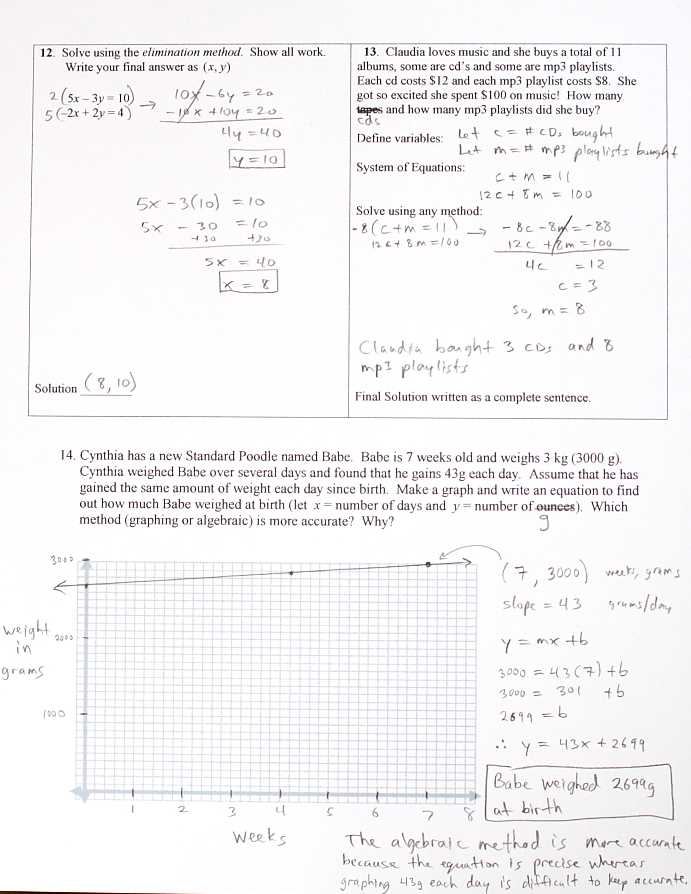
This section provides a detailed guide to solving various mathematical problems related to linear equations, functions, and their applications. By reviewing each problem step-by-step, you can gain a deeper understanding of how to manipulate expressions, solve for unknowns, and interpret mathematical relationships. The goal is to enhance your ability to approach different types of equations and inequalities with confidence.

By mastering these techniques, you will not only improve your problem-solving skills but also build a solid foundation for tackling more complex concepts in future studies. Understanding the methods used to solve these exercises will equip you with the tools needed to handle a wide range of mathematical challenges. Practice and review are key to achieving proficiency and ensuring long-term success.

To further aid your learning, each solution is broken down into simple steps, highlighting the strategies and key principles behind each one. Whether you are reviewing or learning these techniques for the first time, the clarity of these solutions will help you feel more confident in your ability to apply them independently. Keep practicing to solidify your understanding and prepare for more advanced topics in mathematics.

Understanding Key Concepts in Chapter 6

This section delves into essential mathematical principles that form the foundation for solving equations and working with functions. Mastery of these concepts is vital for progressing through more advanced topics. By understanding the underlying techniques and strategies, you will be better equipped to approach a wide range of problems with confidence and clarity.

The key to success in this area lies in grasping the fundamental relationships between variables, and how to manipulate them to solve for unknowns. A deep understanding of these concepts allows you to simplify complex expressions and effectively interpret the results. Below is a breakdown of the most important principles covered in this section:

Concept	Description
Linear Equations	Equations involving variables raised to the first power, often solved by substitution or elimination methods.
Graphing Techniques	Methods for plotting equations on a coordinate plane to visualize relationships between variables.
Systems of Equations	Solving for multiple unknowns by finding where two or more equations intersect.
Word Problems	Translating real-world scenarios into mathematical equations and solving for unknowns.
Functions	Understanding the relationship between inputs and outputs, often represented in tables, graphs, or equations.

By mastering these key concepts, you will not only enhance your ability to solve problems in this section but also prepare for more advanced mathematical challenges in future lessons.

Step-by-Step Solutions for Exercises

This section provides detailed, easy-to-follow solutions for a variety of mathematical problems, allowing you to understand each step in the process. By breaking down complex problems into manageable steps, you can build a solid understanding of how to approach and solve similar exercises on your own. These solutions are designed to highlight key strategies and techniques that will help you grasp important concepts and improve your problem-solving skills.

Each solution is carefully explained, ensuring that every step is clear and logically follows from the previous one. This approach allows you to see the progression of thought and the application of mathematical principles in action. Whether you are working through basic problems or more challenging exercises, the step-by-step format will guide you through the process and reinforce your understanding.

Common Mistakes in Algebra 1

Many learners face challenges when working through mathematical problems, especially when dealing with equations and functions. Understanding where mistakes commonly occur is key to improving problem-solving skills and avoiding errors in future exercises. This section highlights some of the most frequent errors encountered in this field and provides guidance on how to avoid them.

One common mistake is misinterpreting the problem’s instructions, leading to incorrect setup or solutions. Another frequent issue is making algebraic simplification errors, such as incorrectly distributing terms or combining unlike terms. Additionally, failing to check the solution by substituting values back into the original equation is a mistake that can easily go unnoticed. By recognizing these typical pitfalls, students can develop more accurate and efficient methods for solving problems.

Mastering Linear Equations and Graphs

Understanding linear equations and their graphical representations is fundamental to mastering more complex mathematical topics. By working with equations involving straight lines, you can develop a deeper understanding of relationships between variables and how to visually interpret those relationships on a graph. This section focuses on techniques for solving and graphing linear equations accurately.

To begin mastering linear equations, it is essential to learn the basic structure of an equation in two variables. Once you are familiar with the equation format, the next step is plotting the equation on a coordinate plane. The ability to graph lines based on their equations will allow you to visualize solutions and interpret their meaning in real-world contexts.

• Identify the slope and y-intercept of the equation.
• Plot the y-intercept on the graph.
• Use the slope to find other points along the line.
• Draw a straight line through the points to complete the graph.

In addition to graphing, solving linear equations involves manipulating the equation to isolate the variable. This process is essential for determining the exact values that satisfy the equation. With practice, you will become proficient in both graphing and solving linear equations, skills that will support your success in future mathematical studies.

How to Solve Systems of Equations

Solving systems of equations involves finding values for variables that satisfy multiple equations at the same time. This is a fundamental skill in mathematics, as it allows you to solve problems where there are interdependent relationships between different quantities. The most common methods for solving these systems are substitution, elimination, and graphing.

Each method has its advantages depending on the specific problem, and knowing when to use each one is key to solving these types of problems efficiently. Below is an overview of the three main techniques used to solve systems of equations:

Method	Description
Substitution	Solving one equation for one variable, then substituting that expression into the other equation to find the second variable.
Elimination	Adding or subtracting the equations to eliminate one variable, making it easier to solve for the remaining variable.
Graphing	Plotting both equations on a graph and identifying the point where the lines intersect, which represents the solution.

Each method can be effective, but the choice of method depends on the structure of the system and the context of the problem. Mastering these techniques will allow you to solve a wide range of problems that involve multiple equations and variables. Practice with each method will help you choose the best approach for any given system.

Real-World Applications of Algebra

The principles you learn in solving equations and working with functions have practical applications in various fields. These mathematical tools are not just theoretical–they help us solve everyday problems, make decisions, and understand complex systems in real life. From budgeting and finance to engineering and computer science, the ability to manipulate variables and solve for unknowns is essential in many professions.

Below are some examples of how mathematical concepts are applied in different industries:

Industry	Application
Finance	Solving equations to calculate interest rates, loans, and investment growth over time.
Engineering	Using equations to design structures, machines, and systems based on specific parameters and constraints.
Computer Science	Applying algorithms and functions to solve problems, manage data, and optimize processes in software development.
Healthcare	Using mathematical models to predict disease spread, calculate dosages, and analyze clinical data.
Manufacturing	Optimizing production lines and supply chains by solving equations related to inventory, demand, and supply rates.

Understanding how to apply these concepts beyond the classroom can give you valuable skills that will benefit you in various careers and everyday decision-making. By honing your problem-solving abilities, you can gain confidence in tackling real-world challenges with mathematical precision.

Strategies for Solving Word Problems

Word problems can be challenging, as they require translating real-world scenarios into mathematical equations. To approach these problems effectively, it’s important to follow a systematic process. By breaking the problem down into manageable steps and using strategies to identify key information, you can solve even the most complex word problems with ease.

Below are some helpful strategies that can guide you through solving word problems:

• Read the problem carefully: Understand the situation described in the problem before jumping into the calculations. Look for key details such as quantities, relationships, and what is being asked.
• Identify variables: Assign a variable to represent the unknown quantity or quantities in the problem. This will help you set up an equation that models the situation.
• Write an equation: Translate the word problem into a mathematical equation by using the relationships described in the text. Be sure to include any necessary operations and constants.
• Solve the equation: Use appropriate methods to solve for the unknown. This could involve simple arithmetic, factoring, or applying algebraic techniques.
• Check the solution: After finding the solution, substitute it back into the original problem to ensure it makes sense within the context of the situation.

By following these steps and practicing regularly, you will become more confident in solving word problems and applying mathematical reasoning to real-world situations.

Tips for Algebraic Simplification

Simplifying expressions is an essential skill when working with mathematical formulas. The goal is to make complex expressions more manageable and easier to work with by applying basic rules of mathematics. Proper simplification helps save time and reduces the risk of errors when solving equations. In this section, we will go over some effective strategies for simplifying expressions efficiently.

Combine Like Terms

One of the most common techniques for simplification is combining like terms. Like terms have the same variable raised to the same power, and they can be added or subtracted directly. This reduces the expression to a simpler form.

• For example, in the expression 3x + 5x, you can combine the terms to get 8x.
• Similarly, in 2y + 4y – y, combining gives 5y.

Apply the Distributive Property

Another useful strategy is to apply the distributive property, which states that a(b + c) = ab + ac. This allows you to remove parentheses and simplify the expression by distributing multiplication across addition or subtraction.

• For example, 3(x + 2) becomes 3x + 6.
• Similarly, 5(2y – 3) becomes 10y – 15.

By mastering these techniques and consistently practicing them, you will be able to simplify complex expressions quickly and accurately. Simplification is a key step in solving problems and helps create a clearer path to finding the solution.

Exploring Functions and Their Properties

Understanding functions is crucial in mathematics as they provide a way to describe relationships between different quantities. A function assigns each input exactly one output, and it can be represented in various forms such as graphs, tables, or equations. Exploring the properties of functions helps to better understand how they behave, how to manipulate them, and how to solve problems involving them.

Types of Functions

There are several types of functions, each with its own characteristics. Some common examples include:

• Linear Functions: These functions have a constant rate of change and can be represented by straight lines when graphed. The general form is y = mx + b, where m is the slope and b is the y-intercept.
• Quadratic Functions: These functions involve squared terms and are represented by parabolas. The general form is y = ax² + bx + c.
• Exponential Functions: Exponential functions involve a constant raised to a variable exponent. They are commonly used to model growth or decay in real-life situations.

Key Properties of Functions

When analyzing functions, there are several important properties to consider:

• Domain: The set of all possible input values (x-values) that the function can accept.
• Range: The set of all possible output values (y-values) that the function can produce.
• Intercepts: The points where the function intersects the x-axis and y-axis. These can provide valuable information about the function’s behavior.
• Increasing/Decreasing: Identifying intervals where the function is increasing or decreasing helps understand the function’s trends.

By studying these properties and understanding the different types of functions, you can solve more complex mathematical problems and model a variety of real-world scenarios. Functions are a fundamental tool in mathematics and provide the foundation for much of higher-level problem-solving.

Solving for Unknown Variables Effectively

Solving for unknown variables is a fundamental skill in mathematics. Whether you’re dealing with simple equations or more complex systems, knowing how to isolate the variable you’re solving for is crucial. By applying the right strategies and techniques, you can solve equations efficiently and accurately.

Step-by-Step Approach

To solve for an unknown variable, it’s important to follow a systematic process. Here are some key steps to consider:

• Identify the equation: Begin by understanding the structure of the equation. Look for the variable that you need to solve for and determine the operations involved.
• Isolate the variable: Use basic operations such as addition, subtraction, multiplication, and division to isolate the variable on one side of the equation. Keep the equation balanced by performing the same operation on both sides.
• Check for extraneous solutions: After solving, always substitute the value of the variable back into the original equation to ensure the solution is valid.

Common Techniques for Solving Equations

Here are some common methods used to solve for unknown variables:

• Substitution: This technique is often used in systems of equations. You solve one equation for one variable and substitute it into the other equation.
• Elimination: In systems of equations, the elimination method involves adding or subtracting equations to eliminate one of the variables, making it easier to solve for the other.
• Factoring: For quadratic equations, factoring can be an effective way to find the roots or solutions by expressing the equation as a product of binomials.

By mastering these strategies and practicing regularly, you’ll be able to solve equations quickly and effectively. Understanding the various methods and knowing when to apply them will significantly improve your problem-solving abilities.

Checking Your Work in Algebra

Verifying your calculations is an essential part of solving mathematical problems. Even the smallest mistake can lead to incorrect results, making it important to check your work thoroughly. By using different methods to confirm your solutions, you can ensure the accuracy of your answers and improve your problem-solving skills.

Methods for Verifying Solutions

Here are several approaches that can help you double-check your results:

• Substitute the solution back: One of the simplest ways to check your work is to substitute the value you found for the variable back into the original equation. If both sides are equal, the solution is correct.
• Use the opposite operation: After isolating the variable, you can reverse the operations to check if the original equation holds true. For example, if you solved by division, try multiplying both sides to see if you reach the original equation.
• Estimate the result: Before solving a problem, estimate the expected answer. After finding the solution, compare it to your estimate. If the results are vastly different, review your work for possible errors.

Common Errors to Watch For

When checking your work, keep an eye out for these common mistakes:

• Sign errors: It’s easy to overlook a negative sign or make an error when applying multiplication or division with negative numbers. Always double-check your signs.
• Arithmetic mistakes: Simple addition, subtraction, multiplication, or division errors can lead to wrong answers. Make sure to perform each step carefully and verify your calculations.
• Misinterpreting the problem: Sometimes errors occur because of a misunderstanding of the question. Reread the problem and ensure that you are solving for the correct value.

By consistently reviewing your work and utilizing these checking techniques, you can minimize mistakes and improve your overall performance in solving mathematical problems. Developing this habit will increase your confidence and efficiency in problem-solving.

Using Algebraic Tools for Success

Effective problem-solving in mathematics often relies on the proper use of various tools and techniques. By understanding how to apply different strategies, students can simplify complex problems and achieve accurate results. Utilizing these tools not only aids in solving equations but also enhances overall mathematical thinking.

Essential Tools for Solving Problems

There are several key resources that can help students approach mathematical challenges with confidence:

• Graphing Calculators: Graphing calculators are invaluable when solving systems of equations or plotting functions. They allow you to visualize relationships between variables and check solutions quickly.
• Mathematical Formulas: Knowing key formulas is essential for solving many types of problems. Whether it’s for finding the area of a shape or solving a quadratic equation, having a formula at hand simplifies the process.
• Online Tools: Numerous websites and apps provide step-by-step solutions, explanations, and practice problems. These can be especially helpful when working through difficult problems or seeking additional clarification.
• Manual Calculations: While technology is useful, manual calculations remain a critical skill. Understanding the basic methods and operations helps build a solid foundation and strengthens problem-solving ability.

Building Success with Proper Techniques

In addition to having the right tools, it’s essential to employ effective problem-solving techniques to maximize success:

• Practice Regularly: Like any skill, proficiency improves with practice. Regularly solving different types of problems helps solidify concepts and improve speed and accuracy.
• Break Problems into Steps: Complex problems can often be daunting. Breaking them into smaller, manageable steps allows for a clearer approach and reduces the likelihood of errors.
• Understand the Concepts: Rather than simply memorizing methods, take the time to understand the underlying concepts. This will make it easier to apply the right technique to different problems.

By combining the right tools with effective techniques, students can navigate mathematical challenges with greater ease and confidence, ultimately achieving success in their studies.

Importance of Practice in Algebra

Consistent practice is a cornerstone of mastering mathematical concepts. Without regular exercises, it can be difficult to fully internalize the processes needed to solve complex problems. Practicing regularly reinforces key skills, helping students build a stronger understanding and the ability to approach a variety of questions with confidence.

Why Practice Matters

Mathematics is a subject where skills are built layer by layer. Each new topic often relies on concepts learned previously, and without ample practice, it becomes harder to retain and apply these concepts effectively. Here’s why practice is essential:

• Improves Retention: The more you practice, the more likely you are to remember the steps and formulas needed for solving problems. Repetition helps cement these concepts in your memory.
• Increases Confidence: Regular practice boosts self-confidence as you begin to solve problems more easily and recognize patterns that help guide your thinking.
• Develops Problem-Solving Speed: The more familiar you become with different types of problems, the faster and more accurately you can solve them. This is especially important during exams or timed assignments.
• Reduces Mistakes: Practice helps you become more aware of common errors. Through repeated exercises, you can identify and correct mistakes, reducing their occurrence in the future.

How to Practice Effectively

It’s not just about doing exercises–effective practice requires strategy. Here are some tips to make your practice sessions more productive:

• Focus on Weak Areas: Identify the topics where you struggle the most and dedicate extra time to those areas. Strengthening these weak spots will significantly improve your overall performance.
• Vary Your Practice Problems: Work on a diverse range of problems to ensure you understand the different applications of each concept. This will help you adapt to any problem that may appear in tests.
• Set Goals: Set specific, measurable goals for each practice session. This will keep you motivated and give you a clear direction to focus on during your studies.

Ultimately, practice is not just about repetition, but about making intentional progress. By incorporating regular, focused practice into your study routine, you’ll develop the skills needed to excel in mathematics and confidently tackle more challenging topics.

How to Approach Algebraic Challenges

When faced with complex mathematical problems, having a clear approach is crucial. Whether you’re solving equations, working with functions, or analyzing patterns, taking the right steps can simplify even the most difficult tasks. A structured method allows you to break down challenges into manageable parts and approach them with confidence.

Step 1: Understand the Problem

The first step in tackling any mathematical problem is to fully understand what is being asked. Carefully read through the question and identify key elements such as known values, unknown variables, and the type of solution required. Look for any specific instructions or conditions mentioned in the problem that will guide your approach.

• Identify the variables: Clearly define what each symbol represents in the problem.
• Analyze the relationship: Pay attention to how the different variables are related or interact within the equation.

Step 2: Break Down the Problem

Once you understand the question, break it down into smaller, more manageable steps. Divide the problem into parts that you can solve independently. If there are multiple variables or unknowns, identify how they can be isolated or eliminated using different strategies like substitution or elimination.

• Work systematically: Tackle one part of the problem at a time without rushing to conclusions.
• Use known formulas: Refer to any relevant mathematical principles or equations that can help simplify your work.

Step 3: Check Your Work

After solving the problem, it’s essential to verify your solution. Checking your work ensures accuracy and prevents mistakes. Plug your solution back into the original problem to see if it satisfies all conditions. If it doesn’t, revisit your approach and try to identify where things may have gone wrong.

By following a clear, structured method and remaining patient, even the most challenging problems can be solved efficiently. Keep practicing different techniques and stay persistent, as each challenge helps build stronger problem-solving skills for the future.

Resources for Extra Practice

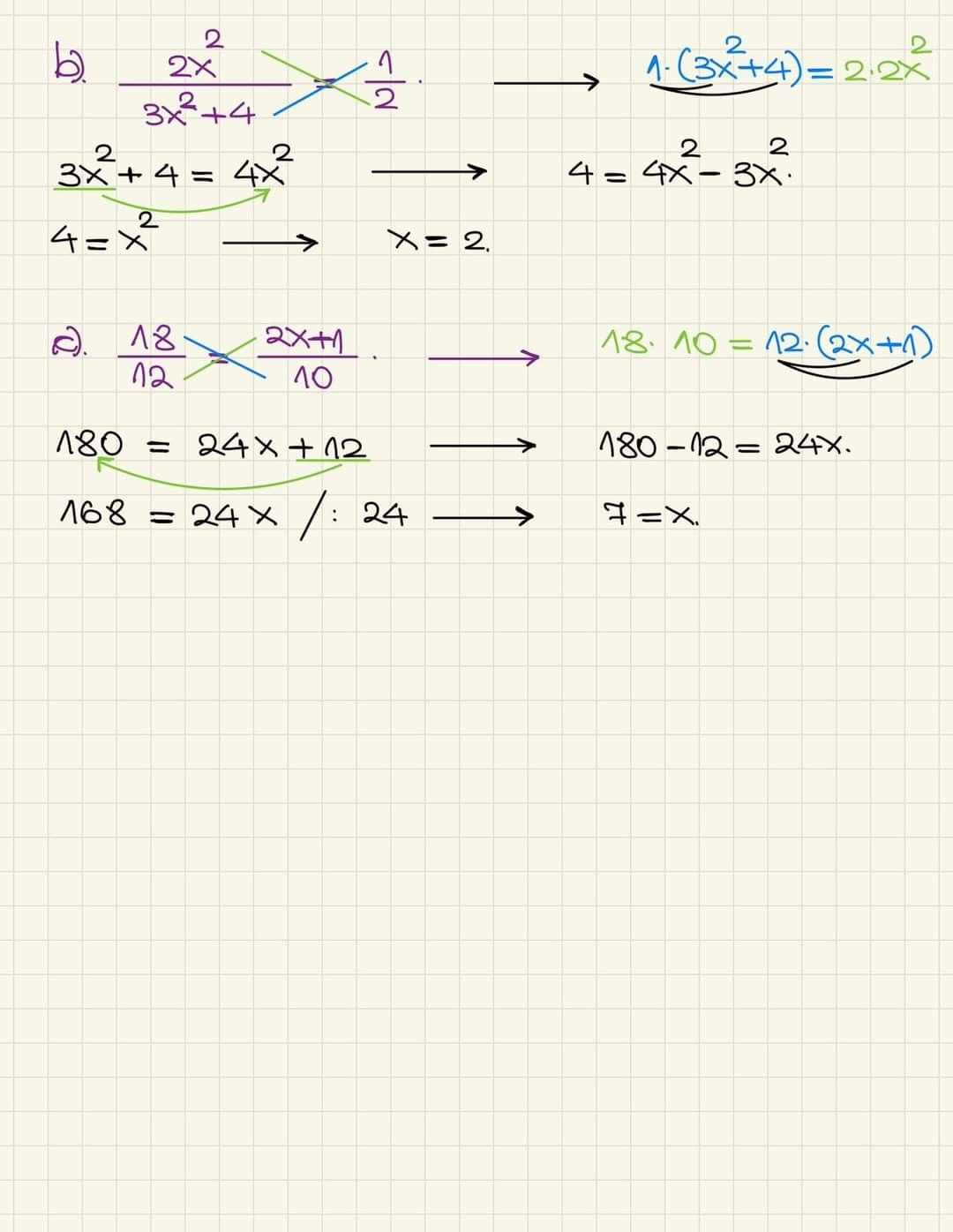
Practicing regularly is key to mastering any mathematical concept. Whether you’re looking to reinforce your understanding or tackle more advanced problems, there are a variety of tools and resources available to help you sharpen your skills. These resources range from online platforms to books, offering a wide range of exercises and explanations to support your learning journey.

Online Platforms

Many websites provide interactive exercises, step-by-step solutions, and explanations to assist in developing a deeper understanding. These platforms often allow you to practice problems at your own pace, track progress, and get immediate feedback. Some popular resources include:

• Khan Academy: Offers a wide range of lessons and practice exercises, from basic equations to more complex topics, with video tutorials and instant feedback.
• Wolfram Alpha: An advanced computational tool that allows you to input problems and see detailed solutions and explanations.
• IXL: Provides tailored practice questions across various topics, with adaptive learning that helps you focus on areas where you need improvement.

Books and Worksheets

Books and printed worksheets are still excellent resources for additional practice. Many textbooks come with practice problems, detailed solutions, and explanations to help reinforce key concepts. Some options include:

• Practice Workbooks: Look for workbooks specifically designed for problem-solving exercises and practice questions, which often include answer keys for self-assessment.
• Textbooks with Practice Sections: Many math textbooks contain practice problems at the end of each section, along with examples to guide you through the process.
• Supplementary Guides: Consider using study guides and problem sets from authors who specialize in mathematics education for additional challenges.

By utilizing these resources, you’ll be able to enhance your skills, build confidence, and prepare for more advanced mathematical tasks. Consistent practice is essential for mastering new concepts, and with the help of these tools, you can make significant progress in your learning journey.

Improving Test Performance

Achieving better results on tests requires more than just understanding concepts; it involves effective preparation and test-taking strategies. By focusing on the right techniques, reviewing key materials, and practicing regularly, you can improve your performance and feel more confident during the exam. Below are several strategies to help you perform at your best during assessments.

Effective Study Techniques

Proper preparation is essential for performing well on tests. To ensure you’re fully ready, consider the following tips:

• Organize Study Sessions: Break down the material into manageable sections and study regularly, rather than cramming the night before.
• Focus on Weak Areas: Identify topics where you struggle and dedicate extra time to understanding them. Seek additional help if needed, whether from a tutor, online resources, or class discussions.
• Practice with Past Tests: Review previous assessments or practice exams to familiarize yourself with the format and question types. This helps reduce test anxiety and improve time management.

Test-Taking Strategies

When it comes time to take the test, implementing the right strategies can make a significant difference in your performance. Keep the following in mind:

• Time Management: Allocate a specific amount of time for each section of the test and stick to it. If you’re stuck on a question, move on and return to it later.
• Read Questions Carefully: Pay attention to the wording of each question. Make sure you understand what is being asked before attempting to solve it.
• Show Your Work: For problems that require calculations or multiple steps, write down your thought process. This will not only help ensure accuracy but also earn partial credit if your final answer is incorrect.

Post-Test Review

After the test, take the time to review your performance. Understand where you made mistakes, and use that as a learning experience for the future. Reflecting on errors can help prevent them from happening again and improve your skills for the next test.

Strategy	Description
Organize Study Sessions	Plan your study time in advance and focus on one section at a time.
Focus on Weak Areas	Identify and dedicate more time to challenging topics.
Practice with Past Tests	Familiarize yourself with the format and question types by practicing with old exams.
Time Management	Allocate specific time for each section and avoid spending too long on any one question.
Read Questions Carefully	Ensure you understand each question before attempting a solution.

By incorporating these strategies into your preparation, you will not only improve your test performance but also gain confidence in your ability to tackle mathematical problems effectively. Regular practice, combined with a well-thought-out approach to studying and test-taking, will set you up for long-term success.

Final Review of Chapter 6 Content

This section provides a comprehensive review of the key topics covered in the previous lessons. The focus is on consolidating understanding and reinforcing the concepts that form the foundation for solving problems. Whether you’re preparing for an exam or seeking to strengthen your grasp of the material, this summary highlights the most important aspects you need to remember and apply effectively.

Throughout this section, the main concepts revolve around equations, their properties, and how to solve them efficiently. The various methods and techniques introduced help in solving complex problems step by step. It’s important to remember the different strategies, as well as the foundational rules, that were emphasized in earlier lessons.

Key topics covered include:

• Solving Linear Equations: A review of the techniques used to isolate variables and find their values. This includes balancing equations and applying inverse operations.
• Graphing Equations: Understanding how to graph linear relationships and interpret their visual representations.
• Working with Inequalities: Solving and graphing inequalities while considering the impact of inequality signs on the solution set.
• Systems of Equations: Techniques for solving systems, whether by substitution, elimination, or graphing methods.

As you review these topics, it is essential to practice problem-solving regularly and test your understanding through various exercises. This will help reinforce the material and enhance your problem-solving skills. Keep in mind that each concept builds on the previous one, so a solid understanding of the basics will make more complex problems easier to approach.

By revisiting these core concepts, you ensure that you are well-prepared to tackle any problems that come your way, whether in assessments or real-life applications. The more you practice and apply these strategies, the more confident and successful you will become in solving mathematical challenges.