
In this section, we delve into essential concepts that help students build a solid foundation in mathematics. The focus is on problem-solving techniques, mathematical reasoning, and the application of various methods to approach complex challenges. These skills are crucial for progressing in higher-level mathematics and for real-world problem-solving.
By breaking down various topics into manageable steps, we aim to make difficult problems more accessible. Emphasis is placed on understanding the underlying principles that drive mathematical solutions. With practice, students will gain confidence in their ability to tackle new problems, regardless of their complexity.
This guide provides clear, structured solutions that help clarify common pitfalls and mistakes. It serves as a resource for students who wish to strengthen their skills and grasp core mathematical ideas with greater ease.
Mathematical Solutions and Problem-Solving Strategies
This section focuses on key problem-solving techniques and methods used to approach mathematical exercises in the given topic. By breaking down the problems into simpler steps, it is possible to understand complex concepts more easily. Whether it’s working through equations or interpreting word problems, a clear strategy is essential for mastering these tasks.
The goal here is to provide a structured approach to solving typical exercises, highlighting common challenges and offering tips to overcome them. The following are important steps to keep in mind when solving related problems:
- Understanding the Problem: Carefully read the problem to identify what is being asked and what information is given.
- Breaking Down the Equation: Simplify the problem by isolating variables and applying appropriate operations.
- Checking the Solution: After solving, it is crucial to verify the result by substituting back into the original equation.
By following these guidelines, students can develop a systematic approach to working through exercises in this area, ultimately gaining confidence and improving their problem-solving skills.
In addition, this guide will offer specific solutions to common problems, providing step-by-step explanations that clarify the reasoning behind each answer. Practice with these examples will help solidify the foundational concepts and prepare students for more advanced topics.
Overview of Key Concepts
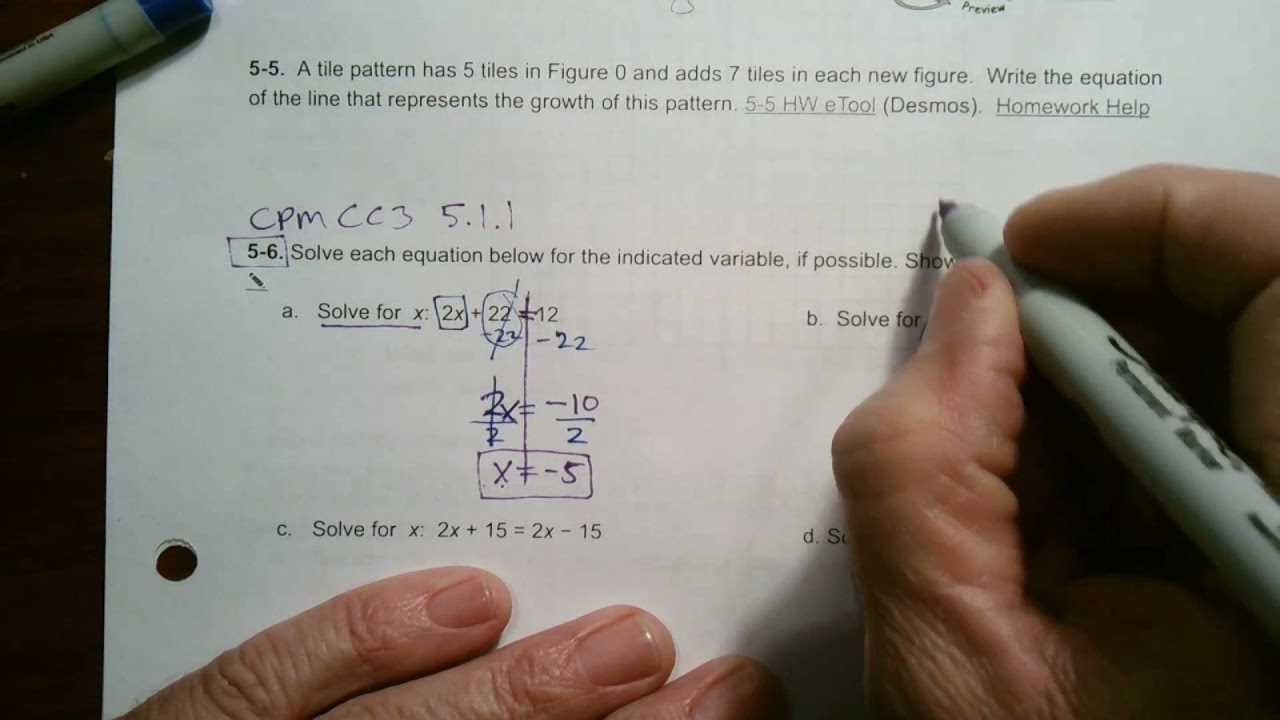
This section covers the fundamental topics essential for mastering the exercises and problems encountered in this part of the course. The focus is on understanding the relationships between numbers and variables, as well as how to apply mathematical rules to simplify and solve complex equations. By grasping these core ideas, students can confidently approach a wide variety of problems.
Essential Skills and Techniques
The following concepts are central to success in this section:
- Identifying Variables: Recognizing how variables function within equations and how they relate to known values.
- Simplifying Expressions: Using appropriate methods to reduce expressions to their simplest form.
- Solving for Unknowns: Applying methods to isolate variables and determine their values in equations.
Approaching Word Problems
Word problems require translating real-world situations into mathematical expressions. The following strategies help break down the process:
- Extracting Relevant Information: Identify key facts and values from the text that will guide the equation-building process.
- Setting Up Equations: Formulating an equation that represents the situation described in the problem.
- Checking Solutions: Verifying the accuracy of the solutions by substituting them back into the original problem.
These strategies, when applied consistently, enable students to tackle a variety of problems with ease and precision.
Key Topics Covered in This Section
This section explores several critical topics that provide a solid foundation for solving various mathematical problems. The emphasis is on understanding fundamental principles, developing problem-solving skills, and applying key techniques to different types of exercises. Mastering these concepts will not only enhance mathematical proficiency but also prepare students for more advanced material.
Among the key areas covered are:
- Understanding Equations: A deep dive into how equations are structured and how to manipulate them to isolate variables.
- Graphing and Functions: Exploring how to represent mathematical relationships visually and interpreting graphs.
- Systems of Equations: Techniques for solving multiple equations that involve two or more variables simultaneously.
- Exponents and Powers: Understanding the rules governing exponents and how to apply them in simplifying expressions.
- Word Problem Strategies: Methods for translating real-world situations into solvable mathematical equations.
These topics are integral to building a comprehensive understanding of the material and will serve as a foundation for tackling more complex mathematical challenges in the future.
How to Solve Mathematical Problems Effectively

Solving mathematical problems requires a systematic approach, where breaking down the steps and understanding each part of the problem is key to finding the correct solution. Whether you are dealing with equations, expressions, or word problems, following a clear method will help simplify complex tasks and lead to better results. Developing strong problem-solving skills is crucial for mastering mathematical concepts.
Step-by-Step Approach
To tackle problems efficiently, it is essential to follow a logical sequence of steps:
- Read the Problem Carefully: Understand what is being asked and identify the known and unknown variables.
- Organize the Information: Arrange the given information in a structured manner, often turning it into an equation or expression.
- Solve Using Appropriate Methods: Apply relevant techniques, such as isolating variables, simplifying expressions, or graphing, depending on the type of problem.
- Verify the Solution: Always check your solution by substituting it back into the original problem to ensure it makes sense.
Common Problem-Solving Tips
Here are some additional tips to improve your problem-solving skills:
- Practice Regularly: The more you practice, the more familiar you become with different types of problems and solutions.
- Learn from Mistakes: Review errors carefully to understand where you went wrong and improve your approach.
- Use Visual Aids: Graphing or drawing diagrams can often make abstract problems easier to understand.
By applying these strategies consistently, you will become more efficient at solving problems and gain confidence in your ability to handle complex mathematical tasks.
Step-by-Step Solutions for Section 5

In this section, we will guide you through detailed solutions for common problems, breaking each down into manageable steps. By following these steps, you will gain a deeper understanding of the concepts and how to apply them to similar exercises. These solutions are designed to help clarify complex processes and provide a clear path to the correct answers.
Below are step-by-step instructions for solving some of the key problems encountered in this section:
| Step | Explanation |
|---|---|
| 1 | Read the problem carefully and identify the known and unknown values. |
| 2 | Set up the equation or expression based on the given information. |
| 3 | Simplify the equation, isolating variables and performing necessary operations. |
| 4 | Check the result by substituting it back into the original problem to verify the accuracy. |
| 5 | Revisit any steps if necessary to ensure the solution is correct. |
These steps will help you approach each problem systematically, making even the most complex tasks more manageable. Practice with these methods will further enhance your problem-solving skills and ensure you are well-prepared for future exercises.
Understanding Mathematical Expressions
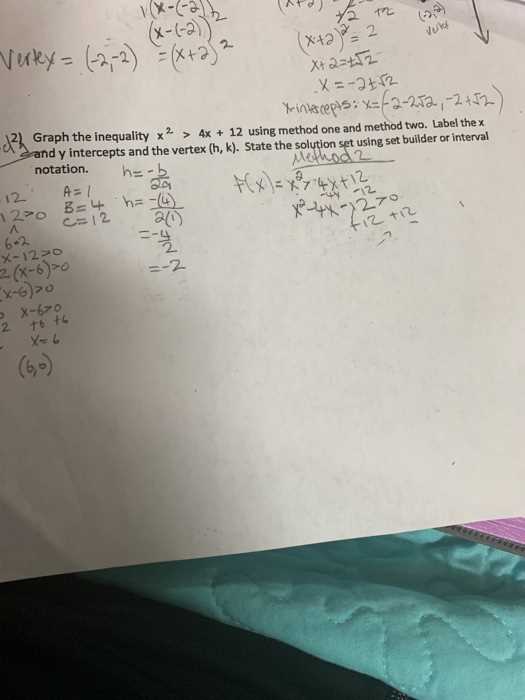
Mathematical expressions form the foundation of many problems, representing relationships between numbers, variables, and operations. Understanding how to interpret and manipulate these expressions is essential for solving equations and real-world problems. The key to mastering these expressions lies in recognizing the role each component plays and how they interact to provide solutions.
Each expression consists of numbers, variables, and mathematical symbols, where the variables can take different values and affect the overall outcome. For example, an expression like 3x + 5 shows a relationship where x is multiplied by 3, and then 5 is added. By substituting different values for the variable, you can evaluate the expression and solve for unknowns.
It is important to recognize the order of operations when working with expressions. Performing operations in the correct sequence ensures accurate results. This includes operations like addition, subtraction, multiplication, and division, along with more complex functions such as exponents or roots.
Common Mistakes in Mathematical Problems
When solving mathematical problems, certain mistakes are more frequent, especially when dealing with complex equations or word problems. These errors can lead to incorrect solutions and confusion, but understanding where they typically occur can help in avoiding them. Recognizing common pitfalls and developing strategies to address them is an essential step in mastering the material.
One common mistake is misinterpreting the problem. Often, students may overlook important details or fail to translate a word problem into a correct mathematical expression. This can lead to setting up the wrong equation and, consequently, arriving at an incorrect answer.
Another frequent issue is incorrect application of the order of operations. When working with multiple operations within an expression, it is crucial to follow the correct sequence (PEMDAS/BODMAS). Neglecting this can result in mistakes, especially when combining addition, subtraction, multiplication, and division.
Lastly, many students forget to check their solutions. After solving for an unknown or simplifying an expression, it’s vital to substitute the result back into the original problem to verify its accuracy. Skipping this step can allow errors to go unnoticed, leading to incorrect conclusions.
Practice Problems and Solutions
Engaging in practice problems is one of the most effective ways to reinforce understanding and gain proficiency in solving mathematical tasks. By applying the concepts learned, students can identify areas where they may need further clarification and improve their problem-solving techniques. Below are several problems with step-by-step solutions to help you practice and grasp key concepts.
Problem 1: Solve the Equation
Given the equation 5x – 3 = 17, solve for x.
- Step 1: Add 3 to both sides of the equation: 5x = 20
- Step 2: Divide both sides by 5: x = 4
- Solution: The value of x is 4.
Problem 2: Simplify the Expression
Simplify the expression 2(3x + 4) – 5x.
- Step 1: Distribute the 2: 6x + 8 – 5x
- Step 2: Combine like terms: x + 8
- Solution: The simplified expression is x + 8.
Practicing problems like these will help reinforce the process of solving equations, simplifying expressions, and improving mathematical fluency.
Helpful Tips for Success in Mathematics
Achieving success in mathematics requires more than just understanding formulas and rules; it involves developing strong problem-solving strategies and consistent practice. By adopting effective study habits and focusing on key concepts, you can improve your skills and build a solid foundation for tackling more advanced topics. Below are some helpful tips to guide you through the learning process and help you succeed.
Effective Study Techniques
- Practice Regularly: The more you practice, the more comfortable you will become with the material. Aim for consistency, even if it’s just a few problems each day.
- Break Down Complex Problems: Break larger problems into smaller, manageable steps. This will make it easier to identify where you might be going wrong and how to fix it.
- Use Resources: Don’t hesitate to seek additional help from tutors, classmates, or online resources when you’re stuck. Different perspectives can provide clarity.
Strategies for Understanding Key Concepts
- Understand, Don’t Memorize: Focus on truly understanding the logic behind each concept rather than just memorizing steps. This will make it easier to apply what you’ve learned in different situations.
- Work on Word Problems: Word problems are a great way to apply theoretical knowledge in practical situations. They also help improve critical thinking skills.
- Review Mistakes: Analyze the errors you make and understand why they happened. This will help you avoid repeating the same mistakes in the future.
By following these tips and maintaining a consistent approach, you’ll develop the skills needed to succeed and gain confidence in solving mathematical problems.
Interpreting Word Problems Effectively

Word problems can often seem challenging, as they require translating a real-world scenario into a mathematical expression. However, with the right approach, interpreting these problems becomes much easier. The key is to break down the information provided, identify the relevant details, and set up an equation that accurately represents the situation.
- Read Carefully: Take the time to read the problem thoroughly. Make sure you understand what is being asked before trying to solve it. Look for keywords that indicate operations, such as “sum,” “difference,” “product,” and “quotient.”
- Identify the Variables: Determine what quantities in the problem are unknown and assign a variable to represent each one. This will help you set up an equation to solve the problem.
- Extract Key Information: Identify the numbers and relationships given in the problem. Often, word problems include unnecessary information, so focus on what is essential to finding the solution.
- Translate Words into Mathematical Expressions: Use your understanding of mathematical operations to convert the words into symbols. For example, “twice a number” translates to “2x,” and “the difference between” suggests subtraction.
- Check Units and Context: Pay attention to units (such as dollars, hours, or miles) and ensure that the answer makes sense in the context of the problem.
By following these steps, you can approach word problems methodically and improve your ability to interpret and solve them with confidence.
How to Use Graphs in Mathematics
Graphs are powerful tools for visualizing relationships between variables and can help to understand complex mathematical concepts more easily. By plotting data points on a coordinate plane, you can observe patterns, trends, and the behavior of equations in a visual form. This section will guide you through the process of using graphs to solve problems and interpret mathematical expressions.
- Plotting Points: To begin using graphs, you need to plot points on a grid. Each point represents a pair of values (x, y) that satisfy a given equation or set of conditions. The x-coordinate shows the horizontal position, while the y-coordinate shows the vertical position.
- Graphing Equations: Graphing an equation allows you to see the relationship between the variables visually. For linear equations, you can plot two points and draw a straight line through them. For more complex functions, such as quadratic or exponential equations, the graph will show curves or other shapes.
- Identifying Slope and Intercept: For linear equations, the graph can help you easily identify the slope and the y-intercept. The slope represents the rate of change, and the y-intercept is the point where the line crosses the y-axis.
- Analyzing Graphs: Once you have graphed an equation, look for key features such as intercepts, turning points, or asymptotes. These features can provide valuable insights into the behavior of the equation and help you solve related problems.
- Using Graphs for Comparison: Graphs can also be used to compare different equations or sets of data. By plotting multiple lines or curves on the same graph, you can visually compare their relationships and find points of intersection or other important features.
Graphs provide a clear and intuitive way to analyze mathematical problems, helping you to understand abstract concepts and make connections between different types of equations and their solutions.
Breaking Down Linear Equations
Linear equations represent a fundamental concept in mathematics, describing relationships where the change in one variable is proportional to the change in another. Understanding how to work with these equations is key to solving many types of problems. In this section, we’ll break down the process of solving linear equations step by step, focusing on identifying their components and applying algebraic techniques to find solutions.
Key Components of a Linear Equation
- Variables: The unknowns in an equation are usually represented by letters such as x, y, or z. These are the values we aim to find.
- Coefficients: The numbers that multiply the variables are called coefficients. For example, in the equation 3x + 5 = 11, the number 3 is the coefficient of x.
- Constants: The constant term is a number without a variable. In the equation 3x + 5 = 11, the number 5 is a constant.
Steps to Solve Linear Equations
- Isolate the Variable: Start by moving all terms with the variable to one side of the equation and constants to the other. This step may involve addition, subtraction, multiplication, or division.
- Simplify the Equation: Combine like terms on each side of the equation to make the equation simpler and easier to solve.
- Solve for the Variable: Once the variable is isolated, solve for its value by performing the necessary operations. Check your work to ensure the solution is correct.
By breaking down linear equations into smaller, manageable steps, you can easily solve for the unknowns and gain a deeper understanding of how these equations model real-world relationships.
Understanding Variables and Constants
In mathematics, variables and constants are two essential components that make up many types of equations and expressions. Understanding the role of each is crucial for solving problems and simplifying mathematical operations. Variables are placeholders for unknown values, while constants are fixed numbers that do not change. By distinguishing between these two, you can manipulate and solve equations more effectively.
Variables represent unknown quantities and are often represented by letters such as x, y, or z. They allow us to generalize equations and functions, making it possible to solve for specific values. Constants, on the other hand, are values that remain the same throughout an equation or expression. They can be positive, negative, or zero, and they provide the numerical basis on which variables operate.
In equations, understanding the relationship between variables and constants is key to simplifying expressions and solving for unknowns. The interaction of variables and constants forms the foundation for algebraic reasoning, making them indispensable in any mathematical analysis.
Solving Systems of Equations
When dealing with multiple relationships between variables, systems of equations are often used to find the values of those variables that satisfy all the given conditions simultaneously. A system consists of two or more equations that are interconnected, and solving these systems involves finding the values for each variable that make all the equations true at the same time. This process is fundamental in many areas of mathematics and real-world problem-solving.
Methods for Solving Systems
- Graphical Method: One way to solve a system is by graphing the equations on the same set of axes. The point where the graphs intersect represents the solution to the system. This method is useful for visualizing the relationships between the equations but may not always be precise.
- Substitution Method: In this approach, one equation is solved for one variable, and that expression is substituted into the other equation. This allows for the elimination of one variable, making it easier to solve for the remaining variable.
- Elimination Method: Also known as the addition or subtraction method, this technique involves manipulating the equations to eliminate one of the variables. By adding or subtracting the equations, the system can be reduced to a simpler form, allowing for easier solving.
Understanding the Solutions
Once the system is solved, there are three possible outcomes:
- One Solution: If the equations intersect at a single point, the system has a unique solution, meaning that there is one set of values for the variables that satisfies both equations.
- No Solution: If the equations represent parallel lines that never intersect, the system has no solution. This means the equations describe contradictory relationships.
- Infinitely Many Solutions: If the equations are dependent, meaning they represent the same line or equation, there are infinitely many solutions, as any point on the line is a valid solution.
By using these methods, systems of equations can be solved efficiently, providing valuable insights into complex relationships between multiple variables.
Utilizing Functions in Chapter 5

In mathematical problem-solving, functions play a crucial role in representing relationships between variables. A function defines how one quantity depends on another, and understanding how to work with these relationships is essential for solving a wide range of problems. In this section, we explore how functions are applied in different contexts and how to effectively use them to find solutions to various equations.
Functions can be used to model real-world situations, make predictions, and solve for unknowns. They help to simplify complex relationships by providing a clear framework for understanding how changes in one variable affect another. By mastering the use of functions, you can enhance your problem-solving abilities and gain a deeper understanding of mathematical structures.
Examples of Functions in Chapter 5
Here are some examples of how functions can be utilized in solving problems:
| Function Type | Description | Example |
|---|---|---|
| Linear Functions | These functions model constant rate changes between two variables. They are represented as straight lines on a graph. | y = 2x + 3 |
| Quadratic Functions | These functions describe relationships where the change in the dependent variable is proportional to the square of the independent variable. | y = x² – 4x + 3 |
| Exponential Functions | These functions describe rapid growth or decay, where the rate of change is proportional to the current value. | y = 2^x |
By understanding these types of functions and knowing how to apply them, you can tackle a variety of problems with confidence. Whether you’re dealing with simple linear relationships or more complex nonlinear functions, these tools are essential for analyzing and solving equations effectively.
Real-World Applications of Algebra
Mathematical concepts are not just confined to textbooks–they play a significant role in solving real-world problems. The skills learned in solving equations, analyzing relationships, and using variables have applications across a variety of fields. By translating practical situations into mathematical models, we can make predictions, optimize solutions, and understand complex patterns that impact our daily lives.
From business to engineering and science, the ability to work with equations and functions is essential. Whether it’s calculating the cost of materials, determining the best route for a delivery, or analyzing scientific data, the tools provided by mathematical reasoning help to make informed decisions. In this section, we explore some of the ways these concepts are applied outside of the classroom.
Finance and Budgeting
In the financial world, equations are used to calculate interest rates, determine investment growth, and assess risks. For example, a simple equation can determine how much money you will have in a savings account after a certain amount of time with compound interest. Additionally, algebra is used in budgeting to allocate expenses and plan for future savings.
- Calculating loan payments
- Budgeting for monthly expenses
- Predicting investment growth
Engineering and Architecture
In engineering, mathematical models are essential for designing structures, systems, and products. Engineers use equations to calculate forces, determine the materials needed, and optimize designs for efficiency and safety. Whether it’s building a bridge, designing a new machine, or planning a city infrastructure, the principles of solving equations are at the heart of it all.
- Designing structures like bridges and buildings
- Calculating load-bearing capacities
- Optimizing product designs for efficiency
Understanding how to apply these mathematical principles in real-life scenarios enhances problem-solving skills and equips individuals with the tools necessary for success in a wide variety of industries.
How Chapter 5 Prepares for Future Topics
The concepts covered in this section lay a solid foundation for more advanced mathematical studies. By mastering the fundamental techniques of solving equations, working with variables, and analyzing functions, students gain essential tools for tackling more complex problems in future lessons. These skills are not only critical for further mathematical topics but also serve as building blocks for a wide range of disciplines, including science, engineering, and economics.
The skills developed in this section are key to understanding more abstract topics, such as systems of equations, graphing, and data analysis. Moreover, the ability to manipulate and solve for unknown values will be essential when moving on to higher-level concepts like quadratic equations, inequalities, and functions in future studies.
Building Problem-Solving Strategies
Understanding the methods introduced in this section equips students with the problem-solving strategies they will use in upcoming lessons. These strategies are essential as the difficulty of problems increases, and mastering basic techniques will allow students to tackle more sophisticated challenges with confidence.
- Recognizing patterns in equations
- Applying algebraic methods to more complex scenarios
- Connecting concepts across different mathematical topics
Foundation for Advanced Topics

As students progress to more advanced subjects, the foundational knowledge gained in this section becomes even more critical. Topics such as calculus, linear programming, and advanced statistics rely heavily on the skills learned here, making this a pivotal part of the learning journey.
- Solving systems of equations in multiple variables
- Understanding the relationships between different types of functions
- Working with matrices and determinants
In conclusion, the lessons from this section are not just isolated concepts but interconnected skills that open doors to a range of mathematical topics that will be explored in the future. Mastering them ensures a smoother transition to more advanced studies and greater success in subsequent courses.
Resources for Further Practice
To reinforce the concepts and skills covered in this section, a variety of resources are available for additional practice. These resources can help solidify understanding, enhance problem-solving abilities, and provide valuable support for tackling more complex tasks. Whether you prefer interactive tools, worksheets, or instructional videos, there are many ways to continue improving your skills outside of regular lessons.
Online Platforms and Tools

There are numerous online platforms that provide interactive exercises, tutorials, and step-by-step solutions. These tools are designed to help students practice at their own pace and receive immediate feedback on their work. Below are some helpful websites and applications:
- Khan Academy: Offers a variety of video lessons and exercises on a wide range of topics, allowing students to work through problems interactively.
- IXL Learning: Provides targeted practice questions with immediate feedback, tracking progress over time.
- Wolfram Alpha: An excellent tool for solving problems step-by-step and visualizing equations and functions.
Books and Worksheets
For those who prefer a more traditional approach, textbooks and worksheets can provide further opportunities for practice. These resources often include examples, exercises, and review sections that are great for reinforcing learned material.
- Math Practice Workbooks: Many publishers offer workbooks that focus on specific topics and include various problem sets for additional practice.
- Textbooks with Solutions: Some textbooks come with answers and explanations, allowing students to check their work and understand the process behind each solution.
Study Groups and Tutoring
Collaborating with peers or seeking tutoring support can also be a great way to reinforce understanding and address any areas of difficulty. Study groups allow students to discuss problems and solutions together, while tutors can offer personalized assistance to work through challenging material.
| Resource | Description | Best for |
|---|---|---|
| Khan Academy | Interactive lessons and exercises | Self-paced learning |
| IXL Learning | Targeted practice and progress tracking | Detailed practice and feedback |
| Wolfram Alpha | Step-by-step solutions and visualizations | Problem-solving support |
By utilizing these resources, students can build confidence, strengthen their understanding of mathematical concepts, and better prepare for future topics. Regular practice and exposure to different types of problems will help ensure long-term success in mastering these important skills.