
The second unit in this math curriculum focuses on building essential skills in solving mathematical problems. This section aims to deepen understanding of various numerical relationships and develop problem-solving strategies that are foundational for more advanced topics. By working through these exercises, students will strengthen their ability to manipulate expressions and interpret different types of equations.
Throughout this unit, you will explore practical techniques for tackling problems step-by-step. Whether it’s working with variables, simplifying expressions, or solving linear equations, this section provides the tools needed to build confidence and improve accuracy in mathematical reasoning. Understanding these core concepts is crucial for success in higher-level mathematics.
As you proceed, remember that consistent practice and attention to detail are key to mastering the material. With each problem solved, you will gain more insight into the underlying principles that govern mathematical operations, making the process easier and more intuitive over time. By the end of this unit, you will be better equipped to approach complex problems with a clear strategy.
Understanding Key Solutions and Methods
This section provides detailed solutions to the problems found in the second unit of the course. It covers essential techniques for solving various types of equations, helping students master important concepts. By carefully reviewing each solution, learners will gain a deeper understanding of how to approach similar problems and improve their problem-solving skills.
Breaking Down the Problem-Solving Process
Each problem is solved step-by-step, illustrating the logical progression required to reach the correct result. This breakdown emphasizes the importance of following a clear method, from identifying key components of the problem to applying the appropriate rules. The solutions provide a roadmap for students to follow, helping them grasp the techniques involved and avoid common mistakes.
Building Confidence with Practice
As students work through these solutions, they can build confidence in their ability to handle similar tasks independently. Repetition and practice are essential to mastering the material, and by understanding the reasoning behind each step, learners can reinforce their knowledge. This section not only offers answers but also the tools to tackle future challenges with confidence.
Understanding Key Concepts in Mathematics
Grasping the fundamental principles of math is essential for solving problems and building more advanced skills. This section focuses on the core ideas that form the foundation of mathematical reasoning. By exploring these concepts, students will enhance their ability to solve a variety of equations and apply these techniques to real-world scenarios.
Breaking Down Mathematical Relationships
Mathematics often revolves around understanding the relationships between numbers, variables, and expressions. Recognizing patterns and learning how to manipulate these elements is crucial for developing problem-solving strategies. This section delves into how different components work together to form logical equations and solutions, helping learners see the connections between abstract concepts and practical applications.
Mastering Problem-Solving Techniques
To effectively tackle mathematical problems, students must master specific techniques and methods. This includes learning how to isolate variables, simplify expressions, and approach equations systematically. With practice, these skills will become second nature, empowering learners to solve even the most complex problems with ease.
Solving Equations in the Second Unit
In this section, we explore the process of solving mathematical equations, focusing on techniques that are fundamental for mastering more complex problems. By systematically applying rules and methods, students will learn how to manipulate different types of expressions and solve for unknown values. Understanding how to solve equations step by step is key to developing confidence in problem-solving.
Steps for Solving Simple Equations
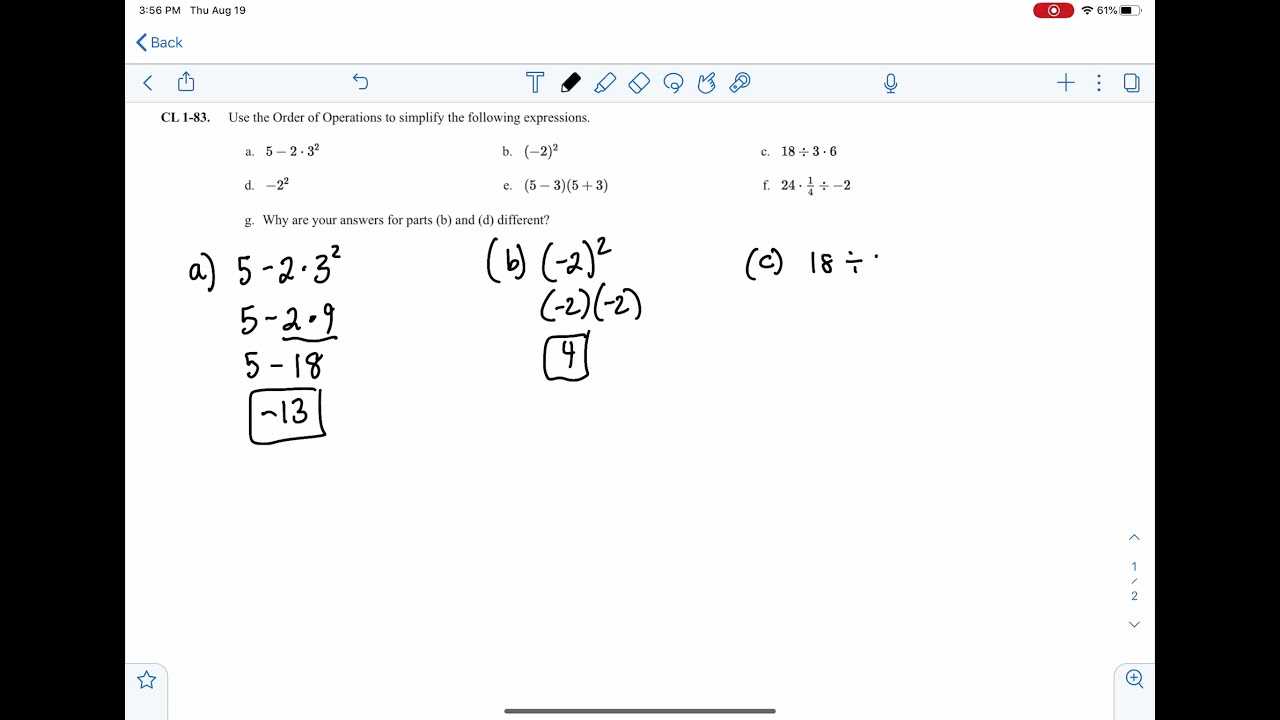
The process of solving equations involves isolating the variable on one side of the equation. This often requires applying inverse operations, such as addition, subtraction, multiplication, and division. Below is a simple example to demonstrate this process:
| Step | Action | Equation |
|---|---|---|
| 1 | Start with the equation | x + 5 = 12 |
| 2 | Subtract 5 from both sides | x = 7 |
Dealing with More Complex Equations

As the complexity of equations increases, students will need to apply additional techniques such as combining like terms or working with fractions. This process often involves multiple steps, but by breaking down each part, students can confidently approach and solve more intricate problems. Practice with various types of equations will reinforce these skills, making the approach more intuitive over time.
Interpreting Word Problems Effectively
Word problems are an essential part of mastering mathematics, as they require students to translate real-world situations into mathematical equations. This process can be challenging, but with the right approach, learners can break down the information step-by-step and solve the problem efficiently. The key is understanding how to identify the relevant details and recognize the operations needed to find the solution.
Key Steps to Approach Word Problems
When tackling a word problem, it’s helpful to follow a structured approach to ensure no important details are overlooked. The following steps can guide students through the process:
- Read the problem carefully – Identify the main question and the information provided.
- Highlight important numbers and terms – Focus on key quantities, units of measurement, and relationships.
- Translate the words into an equation – Convert the narrative into a mathematical expression or equation.
- Solve the equation – Use the appropriate techniques to solve for the unknown.
- Check your work – Verify that the solution makes sense in the context of the problem.
Common Mistakes to Avoid

While working through word problems, students often encounter specific challenges. Being aware of these common mistakes can help avoid confusion:
- Missing key information – Sometimes, important details are buried in the text. Be sure to read carefully.
- Improper interpretation of the question – Make sure you fully understand what is being asked before solving the problem.
- Forgetting to check the units – Always pay attention to the units provided and ensure the final answer is in the correct form.
Step-by-Step Guide to Solutions
Breaking down mathematical problems into manageable steps is essential for solving them correctly and efficiently. This section provides a clear, structured approach to tackling problems, ensuring each stage is carefully addressed. By following this step-by-step method, students can gain confidence and improve their problem-solving abilities.
Essential Steps for Solving Problems
To approach any problem systematically, follow these basic steps:
- Understand the problem – Carefully read the question and identify what is being asked.
- Identify known and unknown values – Highlight key information and determine what needs to be solved.
- Set up the equation – Translate the word problem or given values into a mathematical expression.
- Perform the necessary operations – Apply appropriate mathematical methods to simplify and solve the equation.
- Check your solution – Ensure the result is reasonable and answers the original question.
Tips for Effective Problem Solving
By applying a consistent method, students can streamline their approach and avoid common errors:
- Stay organized – Write out each step clearly and avoid skipping any parts of the process.
- Work through similar examples – Practicing with problems of increasing difficulty helps reinforce techniques.
- Review your calculations – Double-check your work to catch any small mistakes.
Common Mistakes in Mathematics
While working through mathematical problems, it’s easy to make mistakes that can lead to incorrect answers. Understanding the most common errors helps students avoid them and improve their overall problem-solving skills. By recognizing these pitfalls and knowing how to correct them, learners can build confidence and accuracy in their work.
Frequent Errors to Watch For
Here are some of the most common mistakes that students make when solving problems:
- Sign errors – Misplacing a negative sign or incorrectly adding/subtracting signs is a common issue.
- Incorrect distribution – Forgetting to distribute terms correctly, especially with parentheses, can lead to inaccurate results.
- Mixing up operations – Confusing the order of operations or skipping necessary steps often results in errors.
- Misinterpreting the problem – Not fully understanding what the problem is asking can lead to setting up the equation incorrectly.
How to Avoid These Mistakes

To prevent errors, it’s important to develop good habits and follow a structured approach:
- Double-check your work – Always review your calculations and ensure each step is correct.
- Take your time – Rushing through a problem increases the chance of overlooking important details.
- Practice regularly – Familiarity with common problem types helps reduce errors and improves speed.
Graphing Linear Equations Explained

Graphing linear equations is an essential skill that allows you to visually represent relationships between variables. By plotting these equations on a coordinate plane, you can observe patterns and analyze how changes in one variable affect another. Understanding how to graph these equations step by step is crucial for interpreting and solving real-world problems.
To graph a linear equation, you need to identify key components such as the slope and the y-intercept. The slope indicates the steepness of the line, while the y-intercept shows where the line crosses the vertical axis. With these two pieces of information, you can accurately plot the equation and draw the corresponding line.
In most cases, the equation is written in slope-intercept form (y = mx + b), where “m” represents the slope and “b” represents the y-intercept. By substituting values for “x,” you can calculate corresponding “y” values, plot those points, and then connect them to form a straight line. As you practice, you will become more comfortable recognizing different forms of linear equations and graphing them efficiently.
Understanding Variables and Coefficients
In mathematical equations, variables and coefficients play a fundamental role in representing relationships between quantities. A variable is a symbol, usually a letter, that stands for an unknown value or a value that can change. Coefficients, on the other hand, are the numbers multiplied by the variables, indicating how much the variable is scaled or influenced by the equation. Understanding the function of both elements is crucial for solving equations and simplifying expressions.
What Are Variables?
Variables can represent any number or quantity. They allow us to generalize problems and express relationships abstractly. For example, in the equation 2x + 3 = 7, “x” is the variable that can take different values based on the context of the problem. By solving for “x,” we determine its specific value that satisfies the equation.
The Role of Coefficients

Coefficients are the numerical factors attached to variables. In the expression 3y – 5 = 10, the number “3” is the coefficient of “y,” meaning that “y” is multiplied by 3. Understanding coefficients helps in recognizing how the variable’s value is affected by multiplication. Coefficients also help identify the slope in linear equations or the rate of change between variables.
Practical Applications of Algebra 1
The concepts learned in introductory mathematics are not just abstract ideas–they have practical uses in everyday life and various professions. From managing finances to designing technology, the skills gained from understanding equations, variables, and relationships are valuable in many fields. Recognizing the real-world applications of these mathematical principles can help make them more meaningful and easier to grasp.
For instance, algebraic techniques are frequently used in fields like engineering, economics, and computer science. Whether it’s calculating interest rates for loans, predicting trends in business, or solving for unknowns in a system of equations, the principles learned in basic courses provide a foundation for problem-solving in diverse scenarios. Understanding how these skills are applied outside the classroom makes learning more engaging and relevant to future career paths.
Tips for Mastering Algebraic Expressions
Mastering mathematical expressions requires understanding how variables and constants interact within an equation. The key to becoming proficient is practicing the manipulation and simplification of these expressions. Developing a clear approach to handling terms, operations, and their relationships will make solving problems easier and more efficient. Here are some essential tips to help you build a solid foundation and gain confidence in working with algebraic expressions.
First, it is crucial to remember the importance of the order of operations. When simplifying an expression, always follow the proper sequence–parentheses, exponents, multiplication and division, and finally, addition and subtraction (PEMDAS). This ensures that each part of the expression is dealt with correctly. Additionally, combining like terms is an important skill. By identifying and grouping terms that have the same variable, you can simplify the expression and make solving much more straightforward.
Another helpful tip is to break down complex problems into smaller steps. Start by identifying the core components of the expression, and solve each part incrementally. With practice, these steps will become second nature, allowing you to tackle more complicated expressions with ease.
Exploring Functions in Chapter 2
Functions are a key concept in mathematics that describe relationships between two variables. They allow us to understand how one quantity influences another and provide a way to model real-world situations. By examining the properties of functions, we can predict outcomes, analyze trends, and solve problems efficiently. In this section, we will explore how functions are represented, interpreted, and applied in various contexts.
One of the most common ways to express a function is through an equation. For example, in the equation y = 2x + 3, the value of “y” depends on the value of “x.” The number “2” is the coefficient, which determines how much “y” changes as “x” changes, while the constant “3” shifts the value of “y” vertically. Understanding how to manipulate and graph functions is essential for analyzing these relationships visually.
Another important aspect of functions is their domain and range. The domain refers to all possible values that the independent variable (often “x”) can take, while the range represents all possible values of the dependent variable (often “y”). Recognizing the domain and range of a function helps us better understand the limits and behavior of the relationship between the variables.
How to Check Your Answers
Verifying your results is an essential step in problem-solving, ensuring that the solutions you find are correct. Whether you’re working with equations or word problems, checking your work helps you catch errors, refine your methods, and boost your confidence. There are several strategies you can use to confirm your solutions effectively and efficiently.
Here are a few methods to help you check your solutions:
- Substitute your solution back into the original equation: Once you find a solution, plug it back into the equation to see if both sides are equal. If they are, your solution is correct.
- Use estimation: Before solving the problem, estimate the answer. After solving, compare your result to your estimate to check if it falls within a reasonable range.
- Check for consistency: Ensure that each step you took in solving the problem aligns logically with the previous one. If something feels off, go back and reassess that step.
By using these strategies, you can confidently assess whether your solutions are accurate and improve your problem-solving skills over time.
Importance of Practice in Algebra
Repetition and consistent practice are fundamental to mastering mathematical concepts. The more you work through problems, the more comfortable you become with various techniques and methods. This process helps reinforce key ideas, improve problem-solving skills, and ultimately leads to greater confidence in tackling complex equations and expressions. Regular practice not only helps you memorize procedures but also enables you to understand the underlying principles and apply them in new situations.
One of the benefits of frequent practice is that it helps you identify patterns and relationships between different types of problems. With experience, you can quickly recognize the approach needed to solve a particular equation or expression, reducing the time spent on each problem. Over time, this leads to more efficient problem-solving and a deeper understanding of mathematical principles.
To make the most of your practice, it’s important to focus on both variety and repetition. Work on problems that challenge you, and revisit previous concepts to strengthen your grasp on them. Below is a simple table of tips to guide your practice sessions:
| Tip | Description |
|---|---|
| Consistency | Make practice a daily habit to reinforce learning and retention. |
| Variety | Work on different types of problems to enhance your problem-solving skills. |
| Challenge Yourself | Tackle more difficult problems to expand your understanding and push your limits. |
| Review Mistakes | Learn from your errors by reviewing where you went wrong and understanding the correct approach. |
By focusing on consistent practice and applying these tips, you can strengthen your mathematical abilities and build a strong foundation for future learning. Remember, mastery comes with time and effort.
Key Terms and Definitions to Remember

In any mathematical study, understanding key terminology is crucial for grasping the core concepts. Whether you are working with equations, functions, or expressions, having a solid grasp of these essential terms helps you navigate problems more effectively and enhances your overall understanding. Here are some of the most important terms to remember:
- Variable: A symbol, often represented by a letter, that stands for an unknown value in an equation or expression.
- Coefficient: A numerical factor that multiplies a variable within an expression or equation.
- Equation: A mathematical statement that asserts the equality of two expressions, typically containing one or more variables.
- Expression: A combination of numbers, variables, and operations that represents a value but does not include an equality sign.
- Constant: A fixed value that does not change within the context of an equation or expression.
- Term: A single number, variable, or the product of both, which is separated by addition or subtraction in an expression.
- Function: A relationship between a set of inputs and outputs where each input is related to exactly one output.
- Solution: The value or set of values that satisfy an equation or inequality.
By familiarizing yourself with these key terms, you can more easily follow problem-solving processes and communicate effectively in mathematical discussions. A clear understanding of these definitions lays the foundation for success in more advanced topics.
Strategies for Solving Systems of Equations

Solving systems of equations involves finding the values that satisfy multiple equations simultaneously. This is a common challenge in mathematics, and various strategies can help simplify the process. By applying the right method, you can efficiently solve for the unknown variables. Below are some of the most widely used strategies:
- Substitution Method: This technique involves solving one of the equations for one variable and then substituting that expression into the other equation. This reduces the system to a single equation with one variable, making it easier to solve.
- Elimination Method: In this approach, you add or subtract the equations in such a way that one of the variables cancels out. This leaves you with a simpler equation to solve for the remaining variable.
- Graphing Method: By graphing both equations on a coordinate plane, the point where the two lines intersect represents the solution to the system. This method is particularly useful for visualizing the relationship between the equations.
- Matrix Method: For more complex systems, especially those involving three or more equations, matrix methods such as Gaussian elimination or Cramer’s rule can be used. These techniques involve working with augmented matrices to solve the system algebraically.
Each of these methods has its strengths and is suited to different types of systems. Understanding when and how to use them can improve problem-solving skills and efficiency. Whether you are working with linear systems or more advanced sets of equations, these strategies form the foundation of effective mathematical reasoning.
Real-World Uses for Algebraic Skills
The ability to understand and manipulate mathematical expressions is not just valuable in the classroom; it has numerous practical applications in everyday life and various industries. Whether you’re planning a budget, designing a building, or analyzing data, mathematical skills are essential tools. Algebraic reasoning, in particular, plays a crucial role in problem-solving across a wide range of fields. Below are some of the key areas where these skills are frequently used:
- Financial Planning and Budgeting: Managing finances requires an understanding of equations and how to solve them. Whether it’s balancing a personal budget or calculating interest rates on loans, algebra helps individuals and businesses make informed decisions.
- Engineering and Architecture: From calculating the load-bearing capacity of materials to designing structural elements, algebraic concepts are essential in the fields of construction and engineering. It helps ensure that structures are safe, efficient, and cost-effective.
- Computer Science and Software Development: Algorithms, which are at the core of programming, rely on mathematical principles. Developers use algebraic techniques to create software solutions, optimize code, and work with databases.
- Healthcare and Medicine: In healthcare, algebra is used for drug dosage calculations, medical imaging, and even genetic research. It plays a role in interpreting medical data and ensuring the accuracy of treatments and diagnoses.
- Data Analysis and Statistics: Whether it’s analyzing trends, interpreting data, or making predictions, algebraic skills are indispensable in fields like economics, marketing, and scientific research. Data analysts use these techniques to make data-driven decisions and predictions.
These examples illustrate that algebra is not just an academic subject, but a vital skill that supports decision-making and innovation in many professional fields. Mastery of algebraic concepts can open doors to a wide range of careers and improve problem-solving capabilities in everyday life.
Advanced Topics After Chapter 2
Once foundational concepts have been established, it’s time to explore more complex ideas that build on the earlier material. These advanced topics dive deeper into mathematical reasoning, expanding on the principles learned in the initial stages. At this point, learners begin to engage with more sophisticated techniques that are applied in real-world situations and more challenging mathematical problems. The following sections introduce key concepts that extend beyond basic calculations and equations:
| Topic | Description |
|---|---|
| Quadratic Equations | Quadratic equations take the form of ax² + bx + c = 0. Solving these equations involves factoring, using the quadratic formula, and completing the square. These techniques are essential for handling more complex relationships and modeling real-world scenarios. |
| Systems of Inequalities | Solving systems of inequalities involves determining the set of values that satisfy multiple conditions simultaneously. Graphing these systems allows for visualizing the solutions and understanding how different constraints interact. |
| Functions and Graphs | Functions are mathematical relationships that map inputs to outputs. Understanding how to graph and manipulate these functions is essential for analyzing patterns, trends, and predictions in various fields like economics and engineering. |
| Exponential Growth and Decay | This topic covers how quantities grow or decrease at a constant rate, often seen in finance, biology, and physics. Mastery of exponential functions is critical for modeling populations, investments, and other real-world processes. |
| Polynomials | Polynomials are expressions involving sums and products of variables raised to integer powers. Operations on polynomials, including addition, subtraction, and division, are foundational for solving higher-level mathematical problems. |
As students progress, these topics provide a broader mathematical toolkit, preparing them for higher education in math, science, and engineering fields. Mastery of these advanced concepts strengthens critical thinking and problem-solving skills, essential for success in various professional and academic endeavors.
Resources for Further Learning

Once you’ve grasped the basics, continuing your studies with additional materials can deepen your understanding and enhance your skills. There are many resources available that provide additional explanations, exercises, and challenges to reinforce your learning. These tools are especially useful for those who want to expand their knowledge or need extra help in certain areas. Below are some valuable resources for further exploration:
Online Learning Platforms
- Khan Academy: Offers free lessons and exercises on a wide range of mathematical topics, including step-by-step tutorials and practice problems.
- Coursera: Provides access to courses from universities and institutions around the world, many of which cover advanced mathematical topics.
- edX: Similar to Coursera, edX offers both free and paid courses in mathematics, offering structured paths and certificate programs.
- Brilliant: Focuses on interactive problem-solving and critical thinking, offering courses that challenge students to think creatively about mathematical concepts.
Books and Study Guides
- “The Art of Problem Solving” by Richard Rusczyk: A series of books that teach problem-solving techniques and provide advanced problems for more experienced learners.
- “How to Solve It” by George Polya: A classic text that introduces strategies for solving mathematical problems and developing a logical approach to learning.
- Practice Workbooks: Many publishers offer workbooks with additional exercises that allow students to practice and refine their skills in specific areas of mathematics.
Interactive Tools and Apps

- Desmos: A powerful graphing calculator tool that helps visualize functions and explore mathematical concepts interactively.
- GeoGebra: Provides dynamic geometry, algebra, and calculus tools that are helpful for visualizing problems and solutions.
- Wolfram Alpha: An online computational tool that can help solve equations, visualize graphs, and provide step-by-step solutions.
Utilizing these resources will not only help you strengthen your current skills but also expose you to new and more advanced concepts, enabling you to tackle a broader range of problems with confidence.