
Preparing for any challenging assessment requires a deep understanding of the material, strategic problem-solving skills, and the ability to apply learned concepts effectively. This section focuses on guiding students through critical aspects of their coursework, ensuring they are equipped with the tools to tackle difficult questions confidently. With proper preparation, complex problems can be broken down and understood with ease.
In this guide, we explore essential topics, review key strategies for answering problems efficiently, and provide useful tips for improving overall performance. Whether you’re looking to refine your problem-solving techniques or get better at managing time during your test, this article serves as a comprehensive resource to boost your readiness and confidence. It’s not just about knowing the right answers, but understanding the reasoning behind them.
By breaking down complicated ideas into manageable parts, students can approach their studies with clarity and focus. This guide will help you navigate through the material and develop a strong foundation for success, ensuring you’re well-prepared when the time comes to demonstrate your skills.
BYU Algebra 2 Part 2 Final Exam Answers
Success in any rigorous assessment relies on more than just memorization; it requires a strong grasp of key concepts and the ability to apply them under pressure. This section explores how to effectively tackle the challenging questions typically encountered during the later stages of the course. By understanding the material deeply, students can confidently approach complex problems and demonstrate their knowledge clearly and accurately.
To excel, it’s crucial to familiarize yourself with the most common problem types and the strategies used to solve them. In this guide, we break down the essential concepts, highlighting practical techniques to ensure that you’re fully prepared for the assessment. Whether you are reviewing for a cumulative test or focusing on specific problem-solving strategies, this section will provide insight into how to approach various types of questions with confidence.
By concentrating on understanding the core principles, you’ll improve your ability to solve problems efficiently and avoid common pitfalls. With consistent practice and a solid grasp of the material, you will not only be prepared for the assessment but also enhance your overall academic performance.
Understanding the Final Exam Format
Grasping the structure of an assessment is essential for successful preparation. Knowing the format in advance allows students to plan their study strategies effectively and approach the test with confidence. This section outlines the typical organization of the questions, the types of problems you can expect, and how they will be presented. Understanding these elements is key to managing time and ensuring a clear response to each item.
Types of Questions and Problem Styles
Each assessment tends to feature a variety of question types, such as multiple choice, short answer, and longer, more detailed problems that require critical thinking. Being familiar with these different formats helps students to adjust their strategies accordingly. For example, multiple choice questions often test your quick recall and basic understanding, while more detailed questions assess your ability to apply concepts in complex scenarios.
Time Management and Organization
Another important aspect of the assessment is its timing and organization. Each section or problem may vary in the amount of time you should spend on it. Learning to allocate your time wisely ensures that you can complete all sections within the allowed period without rushing or leaving questions unanswered. Practice and mock tests are valuable tools to simulate this experience and improve your pacing.
Key Topics Covered in Algebra 2 Part 2

The second segment of this course delves into a variety of advanced mathematical concepts that build upon earlier knowledge. These topics are designed to challenge students and deepen their understanding of the subject. Mastery of these key areas is essential for performing well in the assessment, as they often form the basis of many questions. In this section, we explore the core subjects that are most frequently tested and provide strategies for effective study.
Functions and Their Applications
A significant portion of the material focuses on functions, including polynomial, rational, and exponential types. Understanding the properties of these functions, how to manipulate them, and their real-world applications is crucial. Topics such as solving for unknowns, graphing complex functions, and analyzing their behavior are fundamental skills that will appear throughout the assessment.
Systems of Equations and Inequalities

Another key area involves solving systems of equations and inequalities, which can appear in various formats. Whether using substitution, elimination, or matrix methods, it is important to be comfortable with multiple techniques. Additionally, understanding how to work with inequalities and their graphical representations is vital for answering related questions efficiently.
Effective Study Tips for Exam Success
Proper preparation is key to excelling in any challenging assessment. To perform at your best, it’s essential to develop effective study habits that help you understand the material deeply and efficiently. This section provides practical tips and strategies to enhance your study sessions, maximize retention, and improve your problem-solving skills. Consistency, focus, and smart planning are the pillars of successful preparation.
Organize Your Study Sessions
Being organized is one of the most important steps in preparing for a test. Create a study schedule that breaks down topics into manageable sections and allocates enough time for each. This will help you stay on track and ensure that you cover all the necessary material before the assessment.
- Set clear study goals for each session.
- Prioritize the most challenging topics.
- Break down your study time into focused intervals, such as 25–30 minutes, with short breaks in between.
Practice Regularly with Sample Problems
Consistent practice is crucial for reinforcing concepts and building confidence. Work through as many sample problems as possible, especially those that are similar to what you might encounter in the assessment. This will help you familiarize yourself with the question types and improve your ability to solve problems under time pressure.
- Start with simpler problems and gradually increase the difficulty.
- Focus on areas where you feel least confident.
- Review incorrect solutions to understand your mistakes and avoid them in the future.
Utilize Additional Resources
In addition to your main study materials, make use of supplemental resources such as textbooks, online tutorials, and practice tests. These resources can provide alternative explanations and new perspectives, helping to deepen your understanding of complex concepts.
- Watch instructional videos on challenging topics.
- Seek out practice exams to simulate the real test environment.
- Join study groups to discuss difficult concepts with peers.
Practice Problems to Master Key Concepts
Mastering key concepts requires consistent practice and a focused approach to problem-solving. By working through a variety of problems, students can strengthen their understanding and develop the skills needed to tackle complex scenarios. This section provides a collection of practice exercises that cover the most important topics, helping you to build confidence and prepare for any challenge that may arise during the assessment.
Problem-Solving with Functions
One of the most critical areas to focus on is understanding how to manipulate and apply functions. Here are some practice problems to help reinforce these concepts:
- Given a polynomial, identify its roots and graph its behavior.
- Solve an equation involving exponential functions and interpret the solution in real-world contexts.
- Find the inverse of a rational function and explain its significance.
Systems of Equations Practice
Another fundamental skill is solving systems of equations. These problems will test your ability to work with multiple variables and find their values using different methods:
- Use substitution to solve a system of two linear equations.
- Apply the elimination method to solve a system involving both linear and quadratic equations.
- Graphically solve a system of inequalities and identify the feasible region.
Graphing and Analyzing Functions
Graphing is an essential skill that can help visualize how equations behave. Work through these problems to sharpen your graphing abilities:
- Graph a piecewise function and explain its different segments.
- Determine the asymptotes and end behavior of a rational function.
- Identify transformations of a function based on its equation and graph.
Time Management Strategies for the Exam
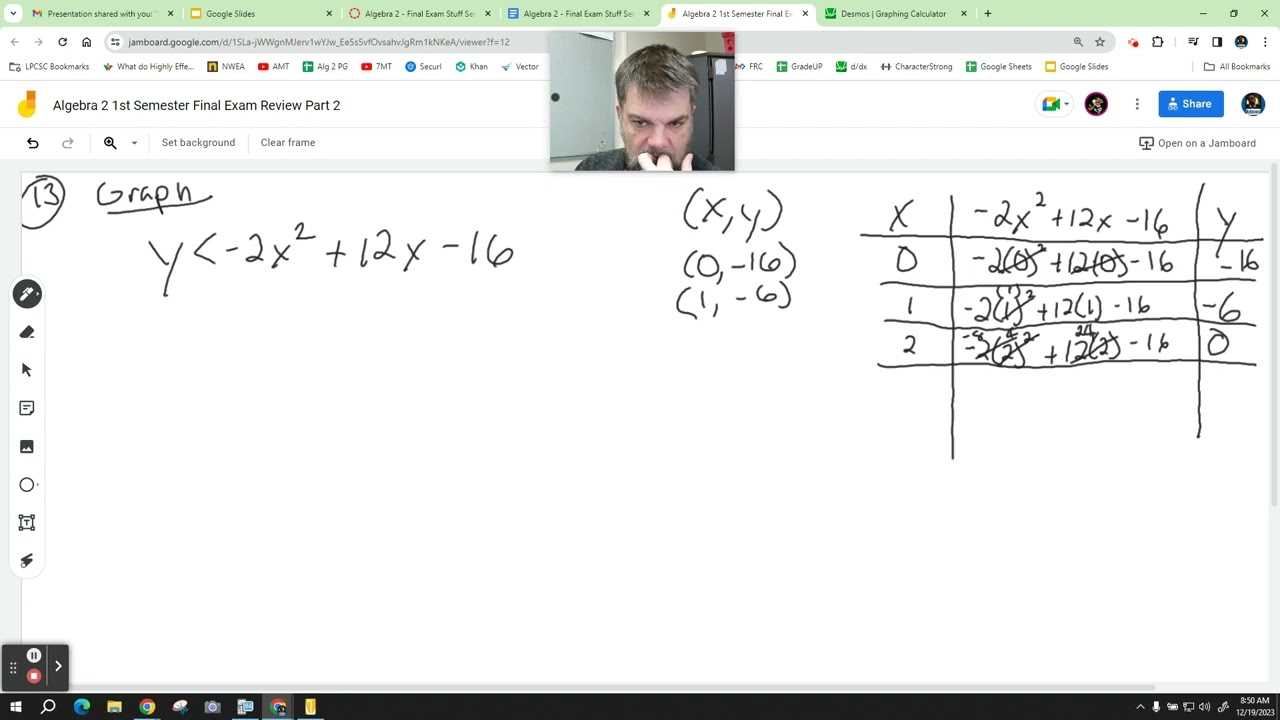
Effective time management is crucial for performing well in any assessment. Without a solid plan, even the most prepared student may struggle to complete the test within the allotted time. This section outlines practical strategies to help you allocate your time wisely, ensuring that you can approach each problem thoughtfully while staying on track.
Prioritize the Most Challenging Questions
Start by identifying the questions that appear most complex or time-consuming. These problems may require more in-depth thinking or involve multiple steps. By tackling them first, you ensure that you have enough time to fully engage with them without feeling rushed later on. Once the difficult questions are out of the way, you can approach the easier ones with greater confidence.
- Skim through the assessment to identify time-intensive problems.
- Begin with the challenging questions and allocate more time to them.
- Move on to easier questions once you’ve tackled the difficult ones.
Set Time Limits for Each Section
Setting clear time limits for each section or question helps you avoid spending too much time on any one problem. Break the overall time into smaller chunks and assign a reasonable amount of time to each part. For example, if you have 60 minutes for 10 questions, aim to spend about 6 minutes per question. This keeps you on pace and prevents you from running out of time before completing all sections.
- Divide the total time available by the number of questions or sections.
- Stick to the time limit for each question to avoid getting stuck.
- Keep an eye on the clock to stay aware of how much time remains.
Review and Refine Your Approach
Once you have completed all the questions, use any remaining time to review your answers. During your review, focus on checking calculations, verifying logic, and ensuring that all parts of each question have been addressed. This final check can help you catch any mistakes you may have missed during your initial attempt.
- Use the last few minutes to double-check your work.
- Look for minor errors that might have been overlooked in the rush.
- Ensure that all answers are complete and clearly written.
Common Mistakes to Avoid During the Test
Even the most prepared individuals can fall into certain traps during an assessment. These common errors often arise from misreading instructions, rushing through questions, or neglecting to double-check work. By recognizing and avoiding these pitfalls, you can improve your performance and ensure that you maximize your chances of success. In this section, we highlight some of the most frequent mistakes and provide tips on how to avoid them.
Misunderstanding the Question
One of the most common mistakes is misinterpreting the question. It’s easy to overlook key details or misread a term, leading to incorrect answers. Always take a moment to carefully read each question, making sure you fully understand what is being asked before attempting to solve it.
- Read the question at least twice to ensure comprehension.
- Highlight or underline important keywords to stay focused.
- Break down the question into smaller parts to understand its requirements.
Rushing Through Problems
Another mistake is rushing through problems in an attempt to finish quickly. While time is limited, working too fast can lead to simple mistakes, such as calculation errors or missed steps. It’s essential to maintain a steady pace, ensuring accuracy over speed.
- Focus on solving each problem carefully and methodically.
- Avoid skipping steps even if you think you know the solution.
- Take short breaks if needed to stay focused and avoid rushing.
Neglecting to Double-Check Work

Failing to review your answers is another common error. Even if you’re confident in your responses, it’s important to double-check your work. This final review can help catch any mistakes or oversights that may have been missed during the initial attempt.
- Set aside time at the end to review your work thoroughly.
- Check for calculation mistakes or overlooked details.
- Ensure that your answers match the format requested in the question.
How to Interpret Algebraic Expressions
Understanding and interpreting algebraic expressions is a fundamental skill needed to solve problems involving variables, constants, and operations. These expressions can appear complex, but breaking them down step by step helps to reveal their meaning. In this section, we explore strategies for interpreting and simplifying such expressions to make them easier to work with.
Identifying Components of an Expression
An algebraic expression consists of several components, including variables, constants, coefficients, and operators. Knowing how to identify and differentiate these elements is the first step toward understanding the expression’s structure.
- Variables represent unknown values and are typically denoted by letters such as x, y, or z.
- Constants are fixed values that do not change, like numbers 3, -7, or π.
- Coefficients are numerical factors that multiply variables, such as the 2 in 2x.
- Operators indicate the mathematical operations to perform, such as +, −, ×, and ÷.
Breaking Down Complex Expressions
When faced with more complicated algebraic expressions, it’s important to break them down into simpler parts. This helps clarify their meaning and enables easier manipulation. Here are some strategies:
- Group like terms: Combine terms with the same variable or exponent. For example, 3x + 4x becomes 7x.
- Use parentheses: Parentheses indicate which operations should be performed first. Always simplify inside parentheses first before expanding.
- Follow the order of operations: Remember PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) when simplifying.
Approaching Word Problems in Algebra
Word problems can often seem overwhelming, especially when dealing with unfamiliar contexts. However, breaking down the information and translating it into mathematical terms is a skill that can make these problems more manageable. In this section, we explore effective strategies for solving word problems by carefully analyzing the language used and identifying the key mathematical elements.
Step-by-Step Approach to Solving Word Problems
To tackle word problems effectively, follow a systematic approach that helps to clearly identify the given information and what is being asked. By translating the problem into an equation, you can apply your mathematical knowledge to find a solution.
- Read the Problem Carefully: Understand the context and identify what is being asked.
- Identify the Variables: Determine what the unknowns are in the problem and represent them with symbols.
- Translate Words into Math: Convert key phrases and information into mathematical expressions.
- Set Up an Equation: Use the information to form a solvable equation.
- Solve the Equation: Apply your algebraic skills to solve for the unknown variable.
- Check the Solution: Verify that the solution makes sense in the context of the problem.
Common Phrases and Their Mathematical Translations
Certain words and phrases commonly used in word problems have specific meanings in mathematical terms. Below is a table that can help you quickly recognize and translate them into algebraic expressions.
| Phrase | Mathematical Translation |
|---|---|
| Sum of | + |
| Difference of | − |
| Product of | × |
| Quotient of | ÷ |
| Is equal to | = |
Tips for Handling Complex Equations
Working with intricate equations can be a daunting task, especially when multiple steps and operations are involved. However, breaking down these problems methodically and applying a few key strategies can simplify the process and lead to accurate solutions. In this section, we provide essential tips for handling equations that might seem complicated at first glance.
Break Down the Equation Step by Step
The first and most important strategy is to approach complex equations one step at a time. Tackling everything at once can lead to confusion and mistakes. Focus on simplifying small parts of the equation before moving on to more challenging components.
- Simplify both sides: Always start by simplifying each side of the equation individually. This might include combining like terms or expanding expressions.
- Isolate variables: Try to get the variable on one side of the equation. This is often the key to making the equation more manageable.
- Perform inverse operations: Use inverse operations to cancel out terms and simplify the equation. For example, if there is addition, use subtraction to eliminate it.
Look for Patterns and Substitutions
Complex equations often contain patterns or opportunities for substitution that can make solving them easier. Identifying these patterns early on can save time and reduce errors.
- Factor when possible: Factoring can simplify a complex expression, especially when dealing with polynomials or quadratic terms.
- Substitute known values: If the equation includes expressions with variables you know or can solve for, substitute those values to simplify the equation.
- Use symmetry: In some cases, equations may exhibit symmetry that can be exploited to reduce the complexity.
Exam Day Preparation Checklist
Preparing for the day of a significant assessment requires careful planning and organization. Ensuring that you have everything you need and are mentally ready can make a big difference in your performance. This checklist will help guide you through essential steps to take the day before and the morning of your assessment, so you feel confident and prepared.
Day Before the Assessment

The day before the test is a crucial time to finalize your preparation. It’s important to focus on review and relaxation, not last-minute cramming. Follow these steps to ensure you are fully prepared:
- Review key concepts: Go over important topics, formulas, and problem-solving techniques one last time.
- Practice sample problems: Complete a few practice questions to refresh your memory and sharpen your skills.
- Organize materials: Ensure you have all necessary materials, such as pens, pencils, erasers, a calculator, or any permitted tools.
- Get a good night’s sleep: Rest is essential for mental clarity, so aim for 7-8 hours of sleep the night before the assessment.
Morning of the Assessment
The morning of the test is when you need to focus on staying calm and confident. A few simple steps can set the tone for a successful experience:
- Eat a healthy breakfast: Have a nutritious meal that will fuel your brain and keep your energy up throughout the assessment.
- Arrive early: Plan to arrive at the test location with plenty of time to spare so you can settle in and avoid unnecessary stress.
- Bring necessary identification: Double-check that you have your ID or any other required documents with you.
- Stay calm and focused: Take deep breaths and trust in your preparation. Stay positive and focused as you begin the assessment.
Resources for Additional Practice

To ensure a deep understanding of key concepts, it is essential to engage with various resources that provide extra practice. Utilizing diverse materials will help reinforce your knowledge and give you a wider range of problems to solve, ultimately improving your ability to tackle challenging questions. Here are some valuable resources to support your preparation and enhance your skills.
Online Platforms and Websites
Many websites offer interactive tools, practice questions, and tutorials that can help you strengthen your grasp on complex topics. These platforms provide instant feedback and allow you to track your progress.
- Khan Academy: This free resource offers comprehensive lessons, practice exercises, and instructional videos on a wide range of subjects.
- EdX and Coursera: Both platforms provide online courses from universities, often including exercises and quizzes to test your understanding.
- Wolfram Alpha: Known for its powerful computational engine, it can be used to check solutions to math problems and explore different methods of solving them.
Books and Workbooks
Books and workbooks are also great for additional practice. These resources provide both guided practice and independent exercises that can deepen your understanding.
- Practice Problem Sets: Look for books with problem sets that offer varying levels of difficulty to challenge your abilities.
- Solution Guides: Books with detailed solutions will help you understand the reasoning behind each step, which can be valuable for learning and improvement.
- Prep Books: Many publishers offer test preparation books that focus on specific skills and techniques for mastering complex concepts.
Understanding Calculator Usage
Calculators are essential tools for solving complex mathematical problems efficiently. Understanding how to effectively use these devices can enhance your problem-solving abilities and save valuable time during assessments. Different types of calculators offer various functionalities, and learning how to utilize these features appropriately can make a significant difference in your performance.
Types of Calculators and Their Functions
There are several types of calculators, each with unique functions suited for different mathematical tasks. Familiarizing yourself with their capabilities will help you choose the right tool for each problem.
| Calculator Type | Functions |
|---|---|
| Basic Calculator | Performs simple operations like addition, subtraction, multiplication, and division. |
| Scientific Calculator | Includes functions for trigonometry, logarithms, and other advanced operations. |
| Graphing Calculator | Capable of plotting graphs, solving equations, and performing complex calculations. |
Maximizing Calculator Efficiency
To maximize the effectiveness of your calculator, consider the following tips:
- Know the functions: Familiarize yourself with the key features and buttons of your calculator to access the necessary tools quickly.
- Use the memory function: Store intermediate results to avoid redoing calculations, saving you time on multiple-step problems.
- Practice with real problems: Work through practice problems using your calculator to become comfortable with the tools and avoid errors during the actual assessment.
Reviewing Key Concepts for Success
Preparing for an assessment requires a solid understanding of essential topics. To ensure success, it’s vital to review the core concepts that are typically tested. By revisiting these areas, you can strengthen your grasp on problem-solving techniques and reduce the chances of overlooking key details during the assessment. A well-structured review can help you feel confident and well-prepared.
Core Topics to Focus On
Focusing on the most frequently tested topics will help you efficiently prepare for the assessment. Below are some of the main areas you should prioritize:
- Equations and Inequalities: Master solving linear, quadratic, and rational equations, as well as understanding how to graph inequalities.
- Functions and Graphs: Understand different types of functions, their properties, and how to interpret and sketch their graphs.
- Polynomials and Factoring: Familiarize yourself with the process of factoring polynomials and solving problems involving polynomial equations.
- Systems of Equations: Be prepared to solve systems using substitution, elimination, or graphing techniques.
Review Strategies for Success
To efficiently review the concepts and ensure that you retain the necessary knowledge, consider the following strategies:
- Practice with Sample Problems: Continuously work through practice problems to reinforce your understanding and identify weak areas.
- Use Conceptual Tools: Diagrams, graphs, and charts can help visualize complex ideas and facilitate understanding.
- Break Down Complex Ideas: For more difficult topics, break them down into simpler steps and tackle each part methodically.
How to Stay Calm During the Test
Staying calm and focused during an assessment is crucial for performing at your best. The pressure of time and the complexity of questions can sometimes cause stress, but managing anxiety is key to maintaining clarity and concentration. By applying a few strategies, you can stay composed and approach the tasks with confidence and a clear mind.
Effective Techniques to Manage Stress
There are several strategies that can help you remain calm and handle challenging situations during the test:
- Deep Breathing: Taking slow, deep breaths helps reduce anxiety and allows you to focus more effectively. Inhale deeply through your nose, hold for a few seconds, and exhale slowly through your mouth.
- Positive Visualization: Before the assessment begins, visualize yourself successfully completing the tasks. This can boost your confidence and reduce feelings of fear or doubt.
- Stay Organized: Keeping track of time and managing your approach to each question can alleviate stress. Don’t rush through questions–prioritize and pace yourself.
Staying Calm During the Test
Once the test begins, it’s important to stay relaxed and focused. Here are some additional tips to maintain calm throughout:
- Take Breaks: If you feel overwhelmed, take a brief mental break. Close your eyes for a few seconds, stretch, or adjust your posture to reset your focus.
- Don’t Dwell on Difficult Questions: If you get stuck on a question, move on and come back to it later. Dwelling on one problem can heighten anxiety and make it harder to move forward.
- Trust Your Preparation: Remember that you have prepared for this moment. Trust in the effort you’ve put in, and focus on applying what you’ve learned, one step at a time.
What to Do After Completing the Test

Once you’ve completed the assessment, it’s important to approach the next steps with the same level of care and mindfulness you applied during your preparation and test-taking. The post-test period is an opportunity to reflect, relax, and focus on what comes next. How you handle the time after finishing can influence your overall well-being and readiness for future challenges.
Review and Reflect
After submitting the test, take a few moments to reflect on your performance. This is not the time to dwell on mistakes, but rather to consider what strategies worked well and where improvements can be made for future assessments:
- Look Back on Your Strategy: Think about how you approached the questions. Did you manage your time effectively? Were there any techniques that helped you stay calm?
- Identify Areas of Difficulty: Take note of any sections that were more challenging. This will guide you in identifying areas to review for the future.
Relax and Recharge
Once you’ve done your part, give yourself permission to unwind. Stressful situations can take a toll, so it’s important to prioritize rest after completing such an important task:
- Engage in Relaxing Activities: Take a walk, read a book, or watch something light to distract yourself and release any built-up tension.
- Celebrate Your Effort: Regardless of the outcome, completing an assessment is an accomplishment. Take a moment to acknowledge the work you put in.