
The fifth unit in this mathematical curriculum covers a range of crucial topics designed to deepen understanding and sharpen problem-solving skills. From simplifying expressions to analyzing advanced functions, this section offers the tools needed to approach complex equations with confidence. By reviewing essential principles, students will be better equipped to tackle challenges both in academic settings and real-world scenarios.
Throughout this section, the focus is on applying various techniques to solve problems efficiently and accurately. Whether it’s working with polynomials, manipulating rational expressions, or exploring exponential relationships, the goal is to build a strong foundation for tackling increasingly sophisticated material in future lessons. Mastering these concepts is key to progressing in higher-level mathematics.
In this guide, we will explore effective methods for solving problems, identify common pitfalls, and provide practical examples. With consistent practice, learners can refine their skills and improve their performance on tests and assignments.
Algebra 2 Chapter 5 Review Answers
This section focuses on providing clear explanations and solutions to key problems covered in the fifth part of the course. It aims to help students consolidate their understanding of various mathematical techniques and methods. Through detailed examples, learners can enhance their ability to solve complex equations and grasp challenging concepts.
Each problem is approached step by step, ensuring a comprehensive breakdown of the process. By reviewing each solution carefully, students can identify the most effective strategies for tackling similar exercises. The goal is not just to provide the correct results, but to help develop a deeper understanding of the underlying principles.
In addition to problem-solving, this section highlights common mistakes and misconceptions, offering guidance on how to avoid them. By recognizing these pitfalls early on, students can improve their accuracy and confidence when faced with similar tasks in the future.
Key Concepts of Algebra 2

This section covers foundational ideas that are essential for solving more advanced problems. Understanding these principles is crucial for developing the skills necessary to work through complex equations and functions. The concepts explored here form the building blocks that support the progression to higher levels of mathematics.
Important Mathematical Techniques
- Factoring and solving polynomial equations
- Working with rational expressions
- Understanding and applying quadratic formulas
- Analyzing functions and their graphs
- Solving systems of equations
Core Mathematical Relationships
- Roots and zeros of functions
- Exponential growth and decay
- Rational and irrational numbers
- Using properties of exponents and logarithms
Mastering these core ideas is essential for anyone progressing through more advanced topics. By becoming familiar with these key concepts, students can approach more challenging problems with confidence and accuracy.
Understanding Polynomial Equations
Polynomial equations are a vital part of solving complex mathematical problems. These expressions involve variables raised to different powers and are central to many topics in higher mathematics. Gaining a strong grasp of these equations allows for efficient manipulation and problem-solving, especially when dealing with real-world scenarios or abstract concepts.
Key Elements of Polynomial Equations
- Terms with varying exponents of a single variable
- Coefficients that multiply each term
- Constant terms that don’t involve variables
Methods of Solving Polynomial Equations

- Factoring the polynomial to find its roots
- Using synthetic division to simplify expressions
- Applying the quadratic formula for second-degree polynomials
- Graphing to visually identify solutions
Mastering these techniques is essential for solving polynomial equations quickly and accurately. Understanding the structure and methods involved ensures that students can tackle a wide variety of problems with confidence.
Factoring Techniques for Algebra 2
Factoring is a powerful tool used to simplify expressions and solve equations. This process involves breaking down complex expressions into their basic components, making it easier to find solutions. A solid understanding of factoring methods is crucial for handling higher-level mathematical problems and solving for unknown variables.
Common Factoring Methods

- Factoring by Grouping: Rearranging terms to create common factors.
- Difference of Squares: Recognizing expressions in the form of a² – b².
- Trinomial Factoring: Factoring quadratics like ax² + bx + c.
- Factoring Completely: Using multiple factoring methods on the same expression.
Steps to Factor Polynomials
- Identify the greatest common factor (GCF) and factor it out.
- Apply the appropriate method based on the number of terms and their structure.
- Check the factored form by expanding to ensure accuracy.
By mastering these techniques, students can break down even the most complicated expressions into manageable parts, leading to faster problem-solving and a deeper understanding of mathematical principles.
Solving Quadratic Equations with Methods
Quadratic equations are a fundamental part of solving for unknowns in mathematics. These equations, typically in the form of a second-degree polynomial, can be solved using a variety of techniques, each with its own advantages. Understanding these methods is essential for efficiently finding solutions and applying them to more complex problems.
Common Methods for Solving
- Factoring: Breaking down the equation into simpler binomials.
- Completing the Square: Rewriting the equation to form a perfect square trinomial.
- Quadratic Formula: Using x = (-b ± √(b² – 4ac)) / 2a to find the roots.
- Graphing: Plotting the equation on a graph to identify the points where it intersects the x-axis.
Choosing the Right Method

- If the equation can be easily factored, factoring is the quickest approach.
- Completing the square is helpful when the coefficient of x² is 1.
- The quadratic formula works universally, even for equations that cannot be easily factored.
By understanding and practicing these methods, students can efficiently solve quadratic equations and tackle more advanced topics with greater ease.
Identifying Functions in Chapter 5

Understanding how to recognize and work with functions is crucial for progressing in mathematics. A function is a relationship between input and output where each input has only one corresponding output. This section will explore various types of functions and methods for identifying them, providing students with the tools to analyze and solve problems efficiently.
Key Features of Functions
- One-to-One Relationship: Each input corresponds to exactly one output.
- Domain and Range: The set of possible inputs and outputs for the function.
- Vertical Line Test: A graphical method to determine if a curve represents a function, where no vertical line crosses the graph more than once.
Types of Functions in This Section
- Linear Functions: Equations with a constant rate of change.
- Quadratic Functions: Functions that form a parabola when graphed.
- Exponential Functions: Functions where the variable appears in the exponent.
By recognizing the characteristics and applying the vertical line test, students can easily identify different functions and determine their properties, ensuring a deeper understanding of how these relationships behave.
Graphing Polynomial Functions Explained
Graphing polynomial functions involves plotting curves that represent relationships between variables, where the degree of the function and the leading coefficient play crucial roles in shaping the graph. Understanding how to interpret the structure of these equations helps in predicting their behavior on a coordinate plane. This section will guide you through the key steps and concepts for graphing polynomial functions effectively.
Steps for Graphing Polynomial Functions

- Identify the degree of the polynomial to determine the end behavior of the graph.
- Find the x-intercepts by solving the equation for zero.
- Determine the y-intercept by evaluating the function at x = 0.
- Analyze the turning points by using the first and second derivative tests, if necessary.
- Plot key points and sketch the curve, considering the behavior at the ends of the graph.
Key Features of Polynomial Graphs
| Feature | Impact on Graph |
|---|---|
| Degree of the Polynomial | Determines the number of turning points and the overall shape of the graph. |
| Leading Coefficient | Indicates the direction the graph opens at the ends (upward or downward). |
| Roots (x-intercepts) | Where the graph crosses the x-axis, indicating the solutions to the equation. |
| Y-intercept | The point where the graph crosses the y-axis, found by setting x = 0. |
By following these steps and understanding the key features of polynomial functions, students can successfully graph complex equations and gain insight into their characteristics. This process helps visualize the solutions and relationships described by the function, making it easier to analyze and interpret results.
Analyzing Roots and Zeros

Understanding the roots and zeros of a function is essential for solving equations and interpreting their behavior. These values represent the points where the function intersects the x-axis, indicating the solutions to the equation. Analyzing the roots and zeros provides valuable insights into the structure of the equation and its graph.
Identifying Roots and Zeros
The roots of a function are the values of the variable that make the function equal to zero. These points are where the graph crosses the x-axis. Identifying the roots is crucial for solving polynomial equations and understanding the relationship between variables.
- Real Roots: Points where the graph crosses the x-axis, corresponding to real solutions.
- Complex Roots: Solutions that do not correspond to x-intercepts, often represented as conjugate pairs.
- Multiplicity of Roots: The number of times a root is repeated, affecting the graph’s shape at the intercept.
Methods for Finding Roots
- Factoring: Breaking down a polynomial into simpler factors to identify the roots.
- Quadratic Formula: A universal method for finding roots of quadratic equations.
- Graphing: Visualizing the function on a graph to locate the x-intercepts.
- Numerical Methods: Using approximation techniques for more complex functions.
By analyzing roots and zeros, students can gain a deeper understanding of how equations behave and how to solve them. This knowledge is fundamental for tackling more advanced topics and provides the foundation for further mathematical exploration.
Working with Rational Expressions
Rational expressions involve fractions where both the numerator and the denominator are polynomials. Manipulating these expressions requires understanding how to simplify, multiply, divide, add, and subtract them. Mastering these operations is essential for solving equations and working with complex mathematical functions.
Key Operations with Rational Expressions
| Operation | Explanation |
|---|---|
| Simplifying | Reduce the expression by canceling out common factors in the numerator and denominator. |
| Multiplying | Multiply the numerators together and the denominators together, then simplify if possible. |
| Dividing | Multiply by the reciprocal of the divisor, then simplify the resulting expression. |
| Adding/Subtracting | Find a common denominator, rewrite the fractions, and combine the numerators. |
Common Mistakes to Avoid
- Forgetting to factor both the numerator and denominator before simplifying.
- Incorrectly adding or subtracting without finding a common denominator.
- Failing to check for excluded values, such as values that make the denominator zero.
By practicing these operations, students can confidently work with rational expressions and tackle more advanced mathematical problems. Proper manipulation of these expressions is vital for a deeper understanding of mathematical relationships and solutions.
Finding the Domain of Functions
The domain of a function refers to the set of all possible input values that will produce a valid output. Determining the domain is crucial for understanding the limitations and behavior of a function, especially when working with real-world applications or complex equations. In this section, we will explore how to find the domain of various types of functions and the common restrictions to consider.
Key Considerations When Finding the Domain
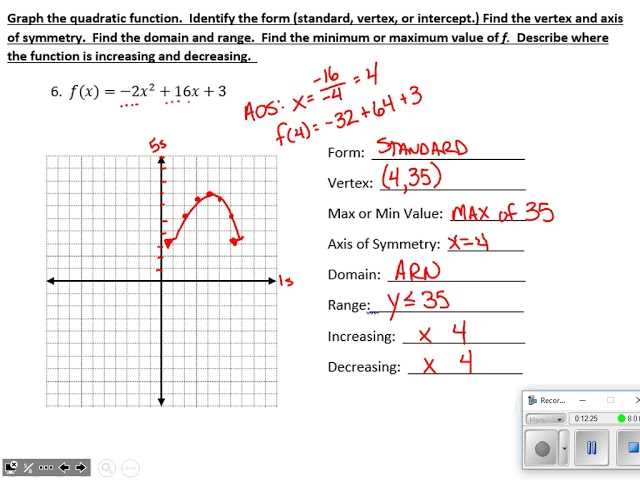
- Division by Zero: Ensure that no input values make the denominator equal to zero, as this would create an undefined result.
- Square Roots: For functions involving square roots or even roots, the radicand (expression inside the root) must be non-negative.
- Logarithms: For logarithmic functions, the argument inside the logarithm must be positive.
- Other Restrictions: Pay attention to any other special conditions that apply based on the type of function.
Steps to Determine the Domain
- Identify any restrictions based on the type of function (e.g., denominators, square roots, logarithms).
- Set up inequalities or conditions that exclude invalid input values.
- Solve for the valid range of input values and express the domain, often as an interval or set notation.
By understanding the domain of a function, you can avoid errors in calculations and ensure that the solutions make sense within the given context. It is a foundational skill for solving and graphing various types of functions accurately.
Exploring Exponential Equations
Exponential equations involve expressions where a constant base is raised to a variable exponent. These equations are prevalent in various fields, such as population growth, radioactive decay, and finance, making them essential to understand. Solving such equations often requires logarithmic methods and properties of exponents to manipulate and isolate the variable in the exponent.
Solving Exponential Equations
To solve exponential equations, we typically start by isolating the exponential term and then apply logarithms to both sides of the equation. This allows us to transform the equation into a form where the exponent is accessible.
- Example: Solve 3^x = 81. By recognizing that 81 is a power of 3, we can rewrite the equation as 3^x = 3^4, and then set x = 4.
- Logarithmic Approach: When the equation doesn’t have a clear base, take the natural log (ln) or logarithm of both sides to eliminate the exponent.
Applications of Exponential Equations
- Growth and Decay: Exponential functions model scenarios like population growth, interest calculations, and radioactive decay, where quantities increase or decrease by a fixed percentage over time.
- Compound Interest: The formula for compound interest is an example of exponential growth, where the amount grows exponentially over time.
- Half-life Calculations: The half-life of substances in decay is another common use for exponential equations, where the amount of substance decreases by half over regular intervals.
Understanding how to solve and apply exponential equations is critical for addressing real-world problems that involve growth, decay, and other time-dependent processes. By mastering the techniques, you can approach these equations with confidence and gain deeper insights into their applications.
Solving Systems of Equations
When faced with multiple equations that share common variables, the goal is to find a solution that satisfies all equations simultaneously. This process, known as solving a system of equations, can be approached through various methods, each suitable for different types of systems. Whether dealing with linear or nonlinear equations, understanding how to manipulate and solve these systems is essential for finding consistent solutions.
Methods for Solving Systems
| Method | Steps | When to Use |
|---|---|---|
| Substitution | 1. Solve one equation for one variable. 2. Substitute this expression into the other equation. |
When one equation can be easily solved for a single variable. |
| Elimination | 1. Multiply or divide equations to align terms. 2. Add or subtract equations to eliminate one variable. |
When the system is set up for easy elimination of a variable. |
| Graphing | 1. Graph each equation on the same coordinate plane. 2. Identify the point where the lines intersect. |
For visualizing solutions or when working with smaller, simpler systems. |
Example of Solving a System

Consider the following system of equations:
1. 2x + 3y = 6
2. x – y = 2
Using the substitution method:
- From the second equation, solve for x: x = y + 2.
- Substitute this expression for x into the first equation: 2(y + 2) + 3y = 6.
- Simplify: 2y + 4 + 3y = 6. Combine like terms: 5y + 4 = 6.
- Solve for y: 5y = 2, so y = 2/5.
- Substitute y = 2/5 into x = y + 2 to find x = 2.4.
The solution to this system is x = 2.4 and y = 2/5.
By understanding and practicing these methods, you can solve more complex systems of equations with ease, whether the equations are linear or nonlinear, and apply these techniques to real-world problems.
Applying the Rational Root Theorem
When working with polynomial equations, especially those with integer coefficients, one useful technique is determining possible rational roots. The Rational Root Theorem provides a systematic way to identify potential rational solutions for a given equation. By examining the relationship between the coefficients of the polynomial, this method allows you to narrow down which rational numbers could be the roots of the equation, simplifying the process of solving it.
According to the theorem, any rational root of a polynomial equation can be expressed as a fraction, where the numerator is a divisor of the constant term and the denominator is a divisor of the leading coefficient. Once the possible rational roots are identified, these candidates can be tested through substitution or synthetic division to find the actual roots of the equation.
Steps for Applying the Rational Root Theorem
- Step 1: Identify the constant term and the leading coefficient of the polynomial.
- Step 2: List all divisors of the constant term (possible numerators) and the divisors of the leading coefficient (possible denominators).
- Step 3: Create a list of possible rational roots by forming fractions from the divisors.
- Step 4: Test each candidate by substituting it into the original equation or using synthetic division.
- Step 5: If a candidate is a root, continue factoring the polynomial. If none work, expand the search to more complex methods.
Example
Consider the polynomial equation:
2x³ – 3x² – 8x + 4 = 0
Using the Rational Root Theorem:
- The constant term is 4, and the leading coefficient is 2.
- The divisors of 4 are ±1, ±2, ±4, and the divisors of 2 are ±1, ±2.
- Possible rational roots are: ±1, ±1/2, ±2, ±4.
By testing each possible root, you can determine that x = 2 is a root of the equation. You can then factor the polynomial further to find other roots.
Through this method, the Rational Root Theorem becomes a powerful tool in polynomial analysis, helping to efficiently find rational solutions for complex equations.
Steps to Simplify Algebraic Expressions
Simplifying mathematical expressions is a crucial skill in solving equations and understanding the underlying relationships between variables. This process involves reducing complex expressions into simpler forms without changing their values. By combining like terms, applying distributive properties, and utilizing basic arithmetic rules, you can make expressions easier to work with and understand. These steps streamline problem-solving and ensure greater accuracy in calculations.
Step 1: Combine Like Terms
Start by identifying terms that have the same variable raised to the same power. These are called “like terms” and can be combined by adding or subtracting their coefficients. For example:
- 3x + 5x = 8x
- 7y² – 2y² = 5y²
By combining like terms, you reduce the complexity of the expression and make it more manageable.
Step 2: Apply the Distributive Property
The distributive property allows you to multiply a single term by each term inside a parentheses. This step is particularly useful when dealing with expressions involving parentheses:
- a(b + c) = ab + ac
- 5(x + 3) = 5x + 15
Expanding the expression ensures that all terms are accounted for and helps further simplify the overall equation.
Step 3: Simplify Fractions (if applicable)

If the expression contains fractions, look for opportunities to simplify by canceling common factors in the numerator and denominator. This can significantly reduce the complexity of the expression:
- Example: 2x/4x = 1/2
By following these basic steps–combining like terms, applying the distributive property, and simplifying fractions–you can reduce complex algebraic expressions to a more simplified form that is easier to manipulate and solve.
Identifying and Graphing Asymptotes

Asymptotes are essential concepts when analyzing rational functions and their graphs. These lines represent values that the function approaches but never actually reaches. Understanding the types of asymptotes–vertical, horizontal, and oblique–can provide crucial insight into the behavior of a function. By recognizing the conditions for these asymptotes, you can accurately sketch the graph and predict the function’s behavior at extreme values.
Vertical Asymptotes
Vertical asymptotes occur when the function approaches infinity or negative infinity as the input value gets closer to a particular number. These lines usually happen where the denominator of a rational expression equals zero, and the numerator does not cancel out. For example, if a function is expressed as f(x) = 1/(x-3), the vertical asymptote occurs at x = 3.
Horizontal Asymptotes
Horizontal asymptotes indicate the behavior of a function as the input values approach positive or negative infinity. These lines help define the end behavior of the graph. For rational functions, if the degree of the numerator is less than the degree of the denominator, the horizontal asymptote will be at y = 0. If the degrees are equal, the horizontal asymptote is at y = ratio of leading coefficients.
Oblique Asymptotes
When the degree of the numerator exceeds the degree of the denominator by one, an oblique (slant) asymptote appears. These asymptotes are linear and indicate that the function approaches a line, but the slope of this line is not horizontal. To find the equation of the oblique asymptote, perform polynomial division.
Graphing asymptotes involves plotting these lines and observing how the function behaves as it approaches them. Understanding their placement allows for a clearer visualization of how the function behaves near undefined points and at large values, aiding in more accurate graphing and analysis.
Common Mistakes in Algebra 2 Chapter 5

When working through advanced mathematical concepts, errors can often occur due to misinterpretation of rules or overlooking key steps. In this section, we will highlight some of the most frequent mistakes students make and provide tips for avoiding them. By identifying these common pitfalls, learners can improve their understanding and approach to solving complex problems.
1. Misunderstanding Exponent Rules
- Incorrectly applying the product rule: For example, x^a * x^b = x^(a+b) is often misapplied when the bases are not the same.
- Confusing the power of a product rule: (ab)^n ≠ a^n * b^n in all cases, especially with negative exponents.
2. Ignoring Domain Restrictions
- Forgetting to exclude values that cause division by zero or lead to undefined expressions, such as when the denominator equals zero in a rational function.
- Not recognizing domain restrictions for functions with square roots or other even powers, where the argument must be non-negative.
3. Failing to Factor Completely
- Leaving terms ungrouped or factoring out only part of the expression can lead to incorrect solutions or an incomplete form of the equation.
- Overlooking common factors between terms when factoring polynomials, which leads to missing or incorrect roots.
4. Mistakes in Graphing Rational Functions
- Forgetting to correctly identify and graph asymptotes, both vertical and horizontal, leading to inaccurate representations of the function.
- Not considering the behavior of the function at extreme values (towards positive or negative infinity) and misinterpreting the end behavior.
5. Incorrect Use of the Quadratic Formula
- Sign errors when calculating the discriminant or plugging in values for b, a, and c.
- Forgetting to simplify the final solution or misinterpreting the roots, especially when the discriminant is negative.
By being aware of these common mistakes and practicing more precise techniques, students can strengthen their understanding and improve their problem-solving skills. Ensuring a step-by-step approach and reviewing key concepts regularly will help avoid these pitfalls and lead to better performance in mathematics.