
In this section, we dive into some of the more complex aspects of mathematics that require a solid understanding of core principles. These topics often involve intricate problem-solving methods and multiple steps to reach the correct solutions. By mastering these techniques, you will be better prepared to handle challenges that arise in higher-level coursework and exams.
The exercises within this section focus on various strategies for simplifying equations, solving for unknowns, and interpreting mathematical functions. Each problem encourages the application of key methods that reinforce your skills and expand your understanding of the subject. The goal is to develop a deeper grasp of mathematical structures and improve your ability to tackle problems with confidence.
Thorough practice and understanding of these concepts can lead to better performance in both academic and real-world scenarios. It’s important to approach each problem systematically, paying close attention to details, and refining your techniques with every exercise. With consistent effort, these methods will become second nature and contribute to your overall mathematical proficiency.
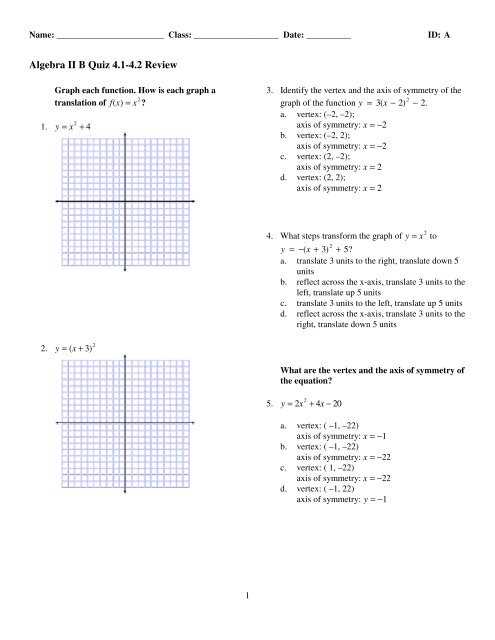
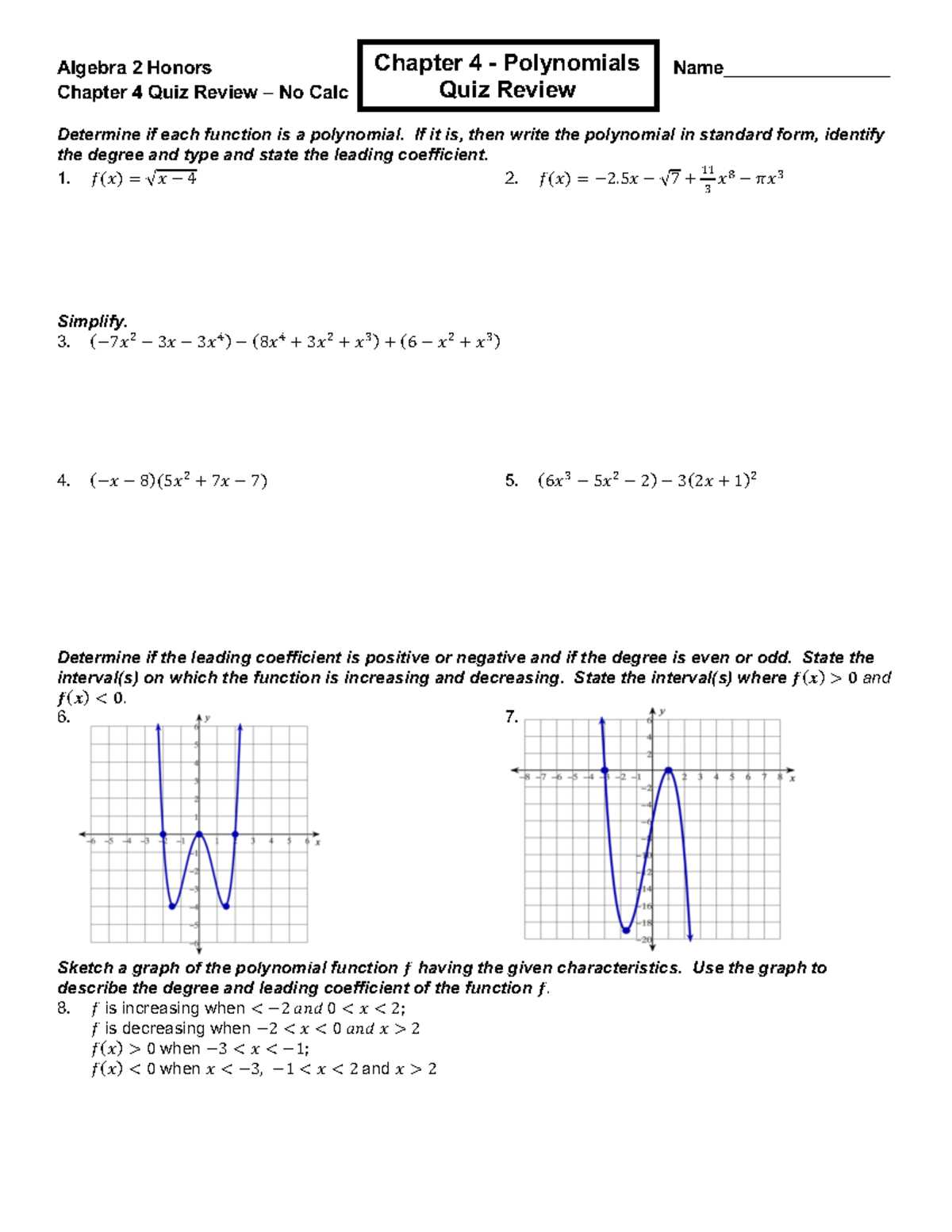
Algebra 2 Chapter 4 Review Answers

In this section, we will explore key mathematical techniques that help solve complex equations and improve problem-solving abilities. This involves breaking down advanced expressions, applying various methods for simplification, and finding solutions step by step. Mastering these techniques is essential for progressing in mathematics and gaining a deeper understanding of its structure.
Solving Quadratic Equations
Quadratic equations are a central focus in this section. These can be approached using methods like factoring, completing the square, and applying the quadratic formula. Each approach offers unique advantages depending on the form of the equation, and practicing these techniques will enhance your ability to quickly identify the best solution strategy.
Working with Rational Expressions
Rational expressions require attention to detail, particularly when simplifying or combining them. Recognizing how to find common denominators, cancel out factors, and handle complex fractions is essential. With careful practice, you can easily manage these expressions and solve them efficiently.
Understanding Key Concepts in Chapter 4
This section focuses on essential mathematical principles that are crucial for solving more complex problems. Gaining a solid understanding of these foundational concepts will allow you to approach difficult equations with greater ease. Each idea builds on previous knowledge and prepares you for more advanced topics, creating a strong base for continued learning.
Working with Functions and Equations
One of the core concepts covered involves the manipulation of functions and equations. Understanding how to solve and graph different types of functions is vital. Whether dealing with linear, quadratic, or rational functions, mastering the rules and operations allows for more efficient problem-solving and helps in recognizing patterns across different types of expressions.
Simplification and Factoring Techniques
Simplification and factoring are key tools that help break down complicated expressions into more manageable forms. By learning how to identify common factors and apply different factoring methods, you can solve problems faster and more accurately. These skills are essential for tackling equations that involve polynomials and rational expressions.
Step-by-Step Solutions for Practice Problems
In this section, we will break down several practice problems to demonstrate the process of finding solutions. Each problem will be approached methodically, highlighting the key steps and explaining the reasoning behind each action. This approach will help reinforce your understanding and give you the confidence to tackle similar problems independently.
Example 1: Solving a Quadratic Equation

Let’s solve a quadratic equation using the quadratic formula. Here’s the step-by-step breakdown:
- Identify the coefficients: For the equation ax² + bx + c = 0, identify the values of a, b, and c.
- Apply the quadratic formula: Use the formula x = (-b ± √(b² – 4ac)) / 2a to solve for x.
- Simplify the expression: Perform the operations under the square root and solve for both values of x.
- Final answer: State the values of x that satisfy the equation.
Example 2: Simplifying a Rational Expression
Now, let’s simplify a rational expression. Follow these steps:
- Factor both the numerator and the denominator: Find common factors in both parts.
- Cancel out common factors: Eliminate any factors that appear in both the numerator and denominator.
- Simplify the remaining expression: After canceling out common factors, the expression should be in its simplest form.
By following these systematic steps, you can efficiently solve problems and gain a deeper understanding of the underlying concepts.
Common Mistakes to Avoid in Algebra 2
When working with advanced mathematical concepts, it’s easy to make errors that can lead to incorrect results or confusion. Understanding these common mistakes and knowing how to avoid them is key to mastering the material and improving your problem-solving skills. By recognizing these pitfalls early, you can approach each problem more confidently and accurately.
Incorrectly Applying the Order of Operations
A frequent mistake is failing to follow the proper order of operations, often referred to as PEMDAS (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction). Skipping steps or misapplying this rule can result in incorrect answers. Always remember to solve expressions inside parentheses first, handle exponents, then proceed with multiplication or division before addition or subtraction.
Forgetting to Factor Completely
Another common error is stopping halfway through the factoring process. It’s essential to factor completely in order to simplify equations or expressions. Leaving a factor unaddressed can make the problem more difficult to solve or cause you to overlook possible solutions. Be sure to factor fully before moving to the next step in your problem-solving process.
How to Tackle Complex Algebraic Equations
Solving complex equations requires a strategic approach to break down the problem into manageable steps. The key to success is to stay organized, apply the appropriate techniques, and methodically work through each part of the equation. By using systematic strategies, you can simplify even the most challenging expressions and find solutions with greater ease.
Start by identifying the type of equation you’re working with. Whether it’s a quadratic, rational, or polynomial equation, each type has specific techniques for solving it. Look for opportunities to simplify expressions, combine like terms, or factor terms when possible. Always check your work at each step to ensure you’re heading in the right direction.
Another important strategy is to isolate the variable you’re solving for. This often involves moving terms to one side of the equation and simplifying the remaining expression. If necessary, apply operations like factoring, completing the square, or using the quadratic formula to solve for the unknown variable. By staying organized and patient, you can confidently tackle complex problems and find the correct solution.
Breaking Down Polynomial Functions
Polynomial functions are a key area of study and can often seem intimidating due to their complexity. However, understanding the structure of these functions and how to break them down into simpler parts is essential for solving equations and graphing them accurately. The process involves recognizing patterns, factoring terms, and applying various techniques to simplify the function.
Identifying Terms and Degree
The first step in breaking down polynomial functions is identifying the individual terms and their corresponding degrees. Each term in a polynomial consists of a coefficient and a variable raised to a power. By organizing the terms based on their degree, you can better understand the behavior of the function.
| Term | Coefficient | Degree |
|---|---|---|
| 3x² | 3 | 2 |
| -5x | -5 | 1 |
| 7 | 7 | 0 |
Factoring and Simplifying Expressions
Once the terms are identified, the next step is to factor the polynomial expression, if possible. Factoring allows you to express the polynomial in a simpler form, making it easier to solve equations or graph the function. Recognizing common factors and applying techniques like grouping or using the distributive property can help simplify the polynomial.
Solving Rational Expressions with Ease
Working with rational expressions can seem complicated at first, but with the right approach, they become much easier to handle. These expressions involve fractions where both the numerator and the denominator are polynomials. By applying systematic techniques like simplifying, factoring, and finding common denominators, you can solve these expressions step by step with confidence.
Simplifying Rational Expressions
The first step in solving rational expressions is simplifying them. Look for common factors in the numerator and denominator, and cancel them out when possible. This reduces the complexity of the expression, making it easier to work with in later steps.
Finding Common Denominators
When adding or subtracting rational expressions, it’s crucial to find a common denominator. This may involve factoring both denominators and determining the least common denominator (LCD). Once you have the LCD, you can rewrite the expressions with matching denominators, allowing you to combine the fractions effectively.
Tip: Always check for any restrictions in the denominator. If a factor makes the denominator equal to zero, it must be excluded from the solution set.
Graphing Quadratic Equations and Parabolas
Graphing quadratic equations is an essential skill for understanding the behavior of parabolas. These curves, which are the graphs of quadratic functions, can open upwards or downwards and have a vertex that represents the highest or lowest point on the graph. To graph them accurately, it’s important to follow a structured process that includes identifying key points and understanding the shape of the curve.
Steps to Graph a Quadratic Equation
Here is a step-by-step guide to graphing a quadratic function:
- Identify the vertex: The vertex is the point where the parabola reaches its maximum or minimum value. It can be found using the vertex formula x = -b / 2a, where ax² + bx + c = 0 is the quadratic equation.
- Plot the vertex: Once you know the coordinates of the vertex, plot it on the graph.
- Find additional points: Choose values for x and solve for y to get more points that lie on the curve.
- Draw the axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two equal parts.
- Sketch the parabola: Connect the points in a smooth curve, making sure the graph opens in the correct direction (upwards or downwards).
Key Features of Parabolas
When graphing quadratic functions, understanding the following key features will help you analyze the graph:
- Vertex: The highest or lowest point on the graph.
- Direction of Opening: The parabola can open upwards or downwards depending on the sign of the leading coefficient.
- Axis of Symmetry: A vertical line that passes through the vertex and divides the parabola into two symmetrical halves.
- Intercepts: The points where the parabola crosses the x-axis (real solutions) and y-axis (when x = 0).
Factoring Techniques for Algebra 2 Problems
Factoring is an essential technique in solving various mathematical expressions. By breaking down complex polynomials into simpler factors, you can make equations easier to solve and analyze. Mastering the different factoring methods will help you simplify problems and find solutions efficiently. Whether you’re working with quadratics, trinomials, or higher-degree polynomials, having a solid understanding of factoring is crucial for success.
Common Factoring Methods
There are several methods that can be applied depending on the form of the expression you’re working with:
- Factoring by Grouping: This technique is useful when the polynomial has four terms. You group terms in pairs, factor out the greatest common factor from each pair, and then factor out the common binomial.
- Factoring Trinomials: A common method for quadratics where you factor expressions of the form ax² + bx + c. You look for two numbers that multiply to give ac and add up to b.
- Difference of Squares: This method applies to expressions of the form a² – b². You can factor it as (a + b)(a – b).
- Perfect Square Trinomials: When a trinomial is a perfect square, it can be factored as (a + b)² or (a – b)².
Steps to Factor Complex Polynomials

When factoring more complex polynomials, follow these steps to simplify the process:
- Identify the greatest common factor (GCF): Look for any common factors that can be factored out from all terms in the polynomial.
- Apply appropriate factoring methods: Depending on the structure, use grouping, trinomials, or other factoring techniques as necessary.
- Check your work: After factoring, always multiply the factors back together to ensure they give the original polynomial.
Exploring the Concept of Exponents
Exponents are a fundamental mathematical tool used to express repeated multiplication. When a number is raised to a power, it indicates how many times that number is multiplied by itself. Understanding exponents allows for efficient manipulation of large numbers and provides a basis for more advanced mathematical concepts. From basic operations to more complex applications, mastering exponents is essential for solving a variety of problems.
The concept of exponents can be applied in different ways, such as in simplifying expressions, solving equations, or working with scientific notation. By learning the rules and properties of exponents, you can tackle problems more easily and with greater accuracy. Understanding how to manipulate these powers is crucial for solving problems in various areas of mathematics.
Strategies for Simplifying Radical Expressions
Simplifying radical expressions is an essential skill for working with square roots and higher-order roots. By reducing these expressions to their simplest form, you can make calculations easier and more manageable. The process involves breaking down the radical to eliminate unnecessary complexity, which can lead to more efficient problem-solving.
Key Techniques for Simplification
To simplify radical expressions effectively, consider the following techniques:
- Extract perfect squares: Identify perfect square factors within the radicand (the number inside the radical). For example, √36 simplifies to 6 because 36 is a perfect square.
- Factor the radicand: Break down the radicand into its prime factors and extract any perfect squares, cubes, or higher powers that can be simplified.
- Rationalize the denominator: If the radical expression is in a denominator, multiply both the numerator and denominator by the conjugate to eliminate the radical from the denominator.
Examples of Simplification
Here are a couple of examples to illustrate how simplification works:
- Example 1: √50 can be simplified as √(25 × 2) = 5√2.
- Example 2: 1 / √3 can be rationalized by multiplying both the numerator and denominator by √3, resulting in √3 / 3.
Applying the Distributive Property Effectively
The distributive property is a powerful tool that allows you to simplify expressions and solve equations by distributing multiplication over addition or subtraction. By applying this property, you can break down complex problems into more manageable parts. This method is especially useful when dealing with expressions that involve parentheses or when you need to combine like terms.
Steps for Using the Distributive Property
To apply the distributive property correctly, follow these steps:
- Identify the terms: Look for expressions where a term outside of parentheses is multiplied by terms inside the parentheses.
- Distribute the multiplication: Multiply the term outside the parentheses by each term inside. For example, in a(b + c), distribute a to both b and c, resulting in ab + ac.
- Combine like terms: After distributing, simplify the expression by combining any like terms that appear in the result.
Example Problems
Here are a few examples to illustrate how the distributive property works:
- Example 1: 2(x + 3) = 2x + 6
- Example 2: 3(4y – 5) = 12y – 15
Mastering Systems of Equations in Chapter 4
Systems of equations are a fundamental concept in mathematics, allowing you to find solutions for multiple variables simultaneously. These systems can be solved using various methods, such as substitution, elimination, and graphing. Mastering these techniques provides a structured approach to solving problems where two or more equations are involved, and understanding how to manipulate them is key to obtaining accurate results.
Key Methods for Solving Systems
To effectively solve systems of equations, it’s essential to understand the different approaches available. Here are the main methods:
- Substitution: In this method, you solve one equation for one variable and substitute the result into the second equation to solve for the other variable.
- Elimination: This method involves adding or subtracting the equations to eliminate one variable, making it easier to solve for the remaining variable.
- Graphing: By graphing both equations on a coordinate plane, you can find the point where the two lines intersect, which represents the solution to the system.
Example of Solving a System

Let’s go through an example of solving a system of equations using the substitution method:
| Equation 1 | Equation 2 |
|---|---|
| 2x + y = 6 | x – y = 1 |
Step 1: Solve one equation for a variable. Let’s solve Equation 2 for x:
x = y + 1
Step 2: Substitute the expression for x into Equation 1:
2(y + 1) + y = 6
Step 3: Simplify and solve for y:
2y + 2 + y = 6
3y = 4
y = 4/3
Step 4: Substitute y = 4/3 back into the expression for x:
x = 4/3 + 1 = 7/3
Thus, the solution to the system is x = 7/3 and y = 4/3.
Reviewing Functions and Their Properties
Understanding the behavior and characteristics of functions is essential for solving complex mathematical problems. Functions describe relationships between sets of numbers, where each input corresponds to a single output. By analyzing the properties of these functions, you can gain deeper insights into their behavior, graph shapes, and transformations. Recognizing the type of function you are working with is the first step toward efficiently solving problems involving variables and equations.
Key Properties of Functions
When working with functions, it’s important to identify their defining properties. Here are some essential properties to consider:
- Domain: The set of all possible input values (independent variables) that the function can accept.
- Range: The set of all possible output values (dependent variables) that result from the given domain.
- Intercepts: The points where the function crosses the axes, typically the x-intercept and y-intercept.
- Symmetry: Functions may exhibit symmetry, such as even symmetry (symmetric about the y-axis) or odd symmetry (symmetric about the origin).
- Asymptotes: Lines that the graph of a function approaches but never touches or crosses, often seen in rational functions.
Common Types of Functions
Different types of functions have distinct characteristics and behaviors. Here are a few commonly encountered types:
- Linear Functions: Represent straight lines and have a constant rate of change, often written in the form y = mx + b.
- Quadratic Functions: Produce parabolic graphs and are typically written as y = ax² + bx + c.
- Exponential Functions: Involve a constant base raised to a variable exponent, such as y = a * b^x.
- Rational Functions: Functions expressed as a ratio of two polynomials, often resulting in asymptotes and undefined points.
Analyzing Word Problems with Algebra
Word problems are an essential part of mathematics that require translating real-world situations into mathematical expressions. By carefully reading and understanding the problem, you can break it down into manageable parts and set up equations to find the solution. The key is to identify the variables, relationships between them, and the operations needed to solve for the unknowns. Once these components are clear, you can apply appropriate mathematical techniques to arrive at the correct answer.
Steps to Solve Word Problems
To effectively solve word problems, follow these general steps:
- Read the problem carefully: Pay close attention to the details provided and underline or highlight important information.
- Identify the unknowns: Determine what quantities need to be found and assign variables to them.
- Translate the words into equations: Convert the relationships described in the problem into mathematical expressions using the variables.
- Set up and solve the equation: Use algebraic techniques to solve for the unknown values.
- Check the solution: Ensure that the solution makes sense in the context of the problem and answer any remaining questions.
Common Types of Word Problems
There are various types of word problems that involve different mathematical concepts. Some common types include:
- Rate problems: These problems involve distances, speeds, or work rates, often using the formula distance = rate × time.
- Mixture problems: These problems deal with combining different substances (such as liquids, chemicals, or costs) to achieve a desired result.
- Age problems: These problems involve relationships between the ages of different people at different times.
- Investment problems: These problems deal with calculating interest or returns on investments based on given rates and time periods.
Using Algebra 2 Review for Test Prep

Effective preparation for any mathematics exam requires a solid understanding of the concepts and the ability to apply them under timed conditions. By reviewing key topics and practicing problem-solving techniques, students can build confidence and improve their performance. Focusing on practice questions and thoroughly working through problems can help reinforce learning and ensure that students are well-prepared for the test environment.
To maximize the benefit of your study sessions, it’s important to focus on areas where you feel least confident. Start by identifying the types of problems that tend to be more challenging, then work through similar problems until the process feels more natural. In addition, reviewing concepts in multiple ways–such as through practice problems, summaries, or visual aids–can help deepen your understanding.
Another effective strategy is to simulate test conditions during your practice sessions. Set a timer and try to solve problems under similar time constraints to those you will face during the actual exam. This will help you develop time-management skills and reduce anxiety when faced with unfamiliar or complex problems on test day.