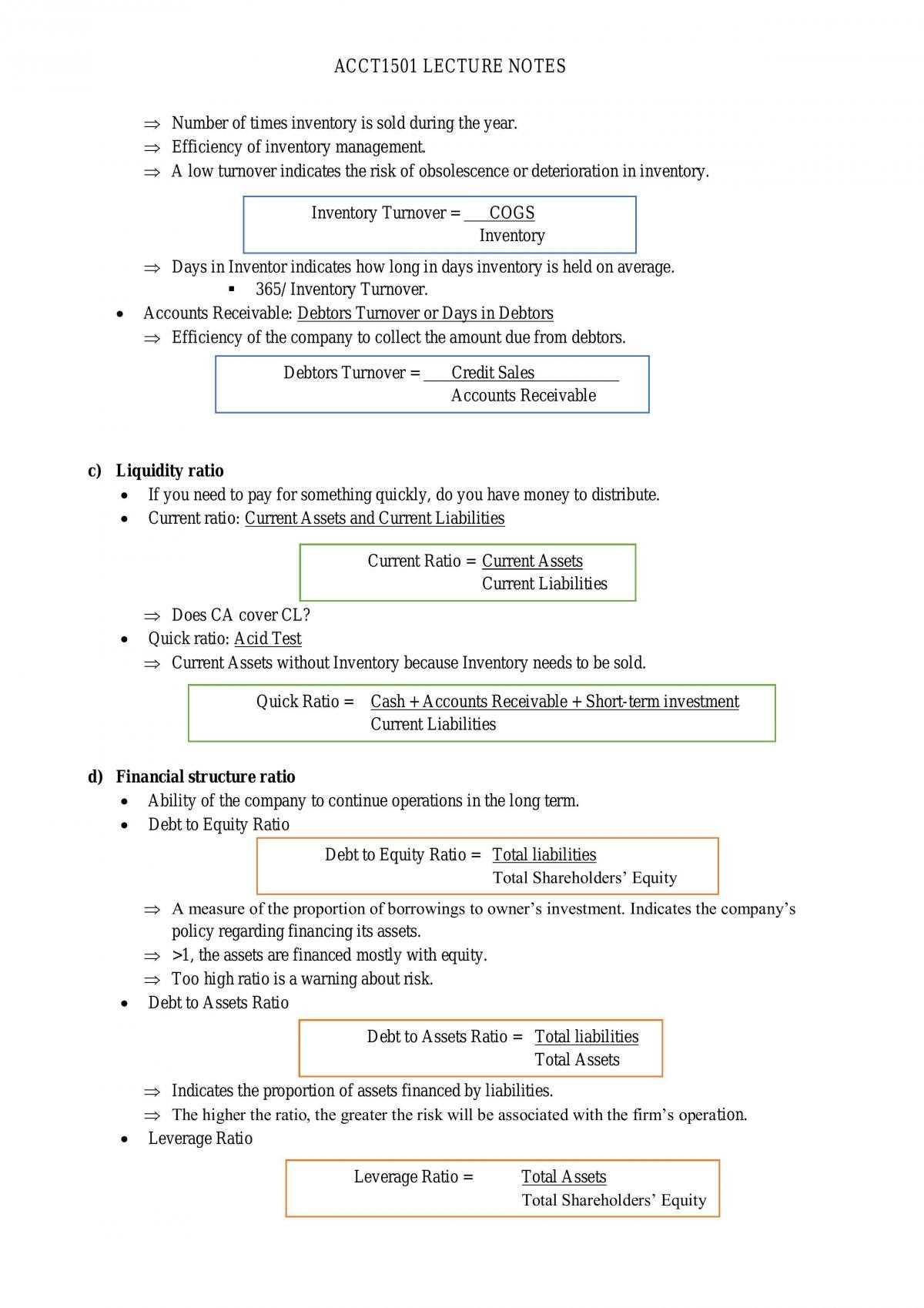
As you approach the end of your course, it’s essential to review key concepts and techniques that will be tested. The upcoming evaluation will assess your understanding of various mathematical principles, requiring you to demonstrate problem-solving skills and critical thinking. Preparing thoroughly can make a significant difference in your performance and boost your confidence.
Understanding the material is the first step towards success. From equations to graphing, a clear grasp of the core topics will enable you to navigate the most challenging problems. This guide will provide insight into common questions and how to approach them effectively, ensuring you are well-equipped for the task at hand.
Effective practice and careful preparation will allow you to approach the assessment with confidence. By revisiting key formulas and strategies, you can ensure that you’re ready to tackle each section with clarity and precision. The goal is to minimize errors and maximize efficiency during the test.
Algebra 1a Final Exam Answers Overview
When preparing for the assessment, it’s important to focus on mastering the essential concepts and techniques that will be tested. The questions are designed to challenge your ability to solve problems efficiently and accurately. By understanding the structure and type of problems you may face, you can approach the evaluation with confidence.
Key areas you should review include:
- Basic mathematical operations
- Working with equations and inequalities
- Graphing functions and interpreting graphs
- Polynomials and rational expressions
- Systems of equations and their solutions
- Word problems and real-life applications
Each section of the test will require a unique approach, so familiarity with a variety of problems will help you stay prepared. Be sure to practice solving different types of questions, as this will sharpen your problem-solving abilities and reduce the likelihood of errors during the evaluation.
By identifying common question formats and types of problems, you can streamline your study efforts and improve your chances of success. Reviewing past questions and practicing time management will also ensure you remain calm and efficient when faced with more complex tasks.
How to Approach Your Algebra Exam
Successfully tackling a math assessment requires more than just knowledge of formulas. It’s about how you approach each problem and manage your time. With the right strategy, you can approach even the most challenging tasks with confidence. The key is to stay organized and follow a systematic process for solving each question.
Understanding the Problem
The first step is to carefully read each question. Take a moment to understand what is being asked before attempting to solve it. Identify key information, such as known values, unknowns, and the type of equation or concept involved. This will help you determine the most effective method to use and avoid unnecessary mistakes.
Breaking Down Complex Problems
If you encounter a complicated problem, break it down into smaller, manageable parts. Focus on solving each segment step by step. By isolating the components of a larger problem, you can ensure that no detail is overlooked and that your solution process is as efficient as possible.
Time management is also crucial. Allocate enough time to each section based on its difficulty and length. If a problem seems too time-consuming, move on to the next one and return to it later if needed. This will help you avoid spending too much time on any single question.
Remember, practice and preparation are your best allies. The more problems you solve before the assessment, the more confident you’ll be in your ability to handle a wide variety of questions. Stay calm and focused, and approach each task methodically to achieve the best results.
Key Topics Covered in Algebra 1a
To succeed in your upcoming assessment, it’s important to familiarize yourself with the core subjects that will be tested. These topics form the foundation of your understanding and will appear frequently in various problem formats. Mastering these concepts will not only help you solve questions with confidence but also build a strong mathematical skill set for future challenges.
The following table outlines the key concepts you should focus on:
| Topic | Description |
|---|---|
| Equations | Understanding how to solve linear and quadratic equations, including techniques like substitution and elimination. |
| Functions | Focusing on how to graph, interpret, and work with linear and non-linear functions. |
| Polynomials | Learning how to simplify, factor, and solve polynomial expressions and equations. |
| Systems of Equations | Working with systems of equations using methods such as graphing, substitution, and elimination. |
| Inequalities | Solving and graphing linear and quadratic inequalities. |
| Rational Expressions | Simplifying, multiplying, and dividing rational expressions. |
Focusing on these topics will give you a well-rounded preparation for the assessment. A solid understanding of each area will make it easier to tackle problems and avoid common pitfalls. Be sure to practice solving problems from each category to reinforce your skills and boost your confidence.
Understanding Common Algebraic Concepts
To excel in your upcoming assessment, it’s essential to have a solid grasp of the fundamental mathematical principles that will be tested. Many of these concepts will appear across a variety of problems, so understanding them deeply will help you solve questions more efficiently and accurately. Focusing on the most common concepts will give you a strong foundation to approach a wide range of problems confidently.
Some of the core principles you should focus on include:
- Variables and Constants: Understanding how to manipulate unknowns and fixed numbers in equations is essential for solving most problems.
- Operations: Knowing how to add, subtract, multiply, and divide both numbers and expressions is key to finding solutions.
- Exponents: The rules for working with powers and roots form an integral part of simplifying and solving equations.
- Factoring: Breaking down expressions into their simplest components allows for easier solutions to complex equations.
- Functions: Recognizing the relationship between variables and how to graph and manipulate functions is crucial for many problems.
By mastering these concepts, you’ll be able to recognize patterns in problems and apply the appropriate techniques to solve them. Practicing with different types of problems that incorporate these principles will help reinforce your understanding and make you more confident when it comes time to tackle the assessment.
Strategies for Solving Algebraic Equations
Solving mathematical equations requires a methodical approach to ensure accuracy and efficiency. Whether you are dealing with simple or complex equations, applying the right strategy can simplify the process and lead to quicker solutions. By following a structured approach, you can systematically solve problems and avoid common mistakes.
One key strategy is to isolate the variable. By getting the unknown on one side of the equation and the constants on the other, you can reduce the problem to a simpler form. This technique is useful for both linear and quadratic equations.
Breaking down the equation step by step is another effective approach. Start by simplifying both sides, combining like terms, and removing any unnecessary factors. This process will make it easier to identify the next steps for solving the equation.
Checking your work is crucial. After finding a solution, always substitute the value of the variable back into the original equation to ensure that both sides are equal. This helps identify any errors made during the solving process and reinforces your understanding of the problem.
Additionally, understanding different types of equations, such as linear, quadratic, and rational, will allow you to apply the most appropriate techniques for each case. Practice with a variety of problems will improve your skills and confidence in solving equations accurately.
Tips for Tackling Word Problems
Word problems often present a unique challenge because they require translating real-world situations into mathematical expressions. The key to solving these problems is to break them down into manageable steps and focus on extracting the relevant information. By following a structured approach, you can easily identify the necessary variables and operations needed to find the solution.
Start by carefully reading the problem to understand what is being asked. Pay attention to key terms that indicate mathematical operations, such as “sum,” “difference,” “product,” or “quotient.” These words will help you determine which operations to apply.
Highlighting key information is another effective strategy. Underline or note down important numbers, variables, or relationships mentioned in the problem. This will help you organize the information and avoid overlooking critical details.
Translating words into equations is the next step. Once you’ve identified the relevant data, convert the word problem into an equation or set of equations. This will allow you to apply your mathematical knowledge to solve the problem systematically.
Lastly, always double-check your solution by reading the problem again to ensure that your answer makes sense in the context of the question. This final step helps confirm that you’ve interpreted the problem correctly and avoided any errors during the solving process.
Reviewing Polynomial and Rational Functions
Understanding polynomial and rational functions is essential for solving a variety of mathematical problems. These types of functions appear frequently in both equations and word problems, so a solid grasp of their properties and behavior is crucial. By reviewing key concepts related to these functions, you will be better prepared to handle any questions that involve them.
Start by recalling the general structure of a polynomial function, which is a sum of terms where each term consists of a variable raised to a non-negative integer power. The degree of the polynomial indicates the highest exponent of the variable. Understanding how to add, subtract, and multiply polynomials will help you simplify and solve related equations.
Rational functions, on the other hand, are ratios of two polynomials. It’s important to recognize their domain, as they may have restrictions where the denominator equals zero. When working with rational functions, be sure to simplify the expression whenever possible to avoid complex calculations and identify any potential asymptotes or discontinuities.
To deepen your understanding, practice graphing both types of functions. Polynomial functions typically have smooth curves, while rational functions may exhibit vertical or horizontal asymptotes. Being able to visualize these functions will help you better understand their behavior and how to solve problems involving them.
Mastering Linear Equations and Inequalities

Linear equations and inequalities are fundamental topics that form the foundation for more advanced mathematical concepts. Mastering these topics is essential for solving a wide range of problems, from basic computations to more complex scenarios. Understanding how to approach and manipulate these expressions will significantly improve your problem-solving skills.
When working with linear equations, the goal is to isolate the variable by using basic operations such as addition, subtraction, multiplication, and division. This process allows you to find the value of the unknown in a straightforward manner. To solve inequalities, the approach is similar, but you must also be mindful of the direction of the inequality sign when multiplying or dividing by negative numbers.
- Linear Equations: These equations have the form of ax + b = c, where you need to solve for the variable x.
- Inequalities: Inequalities like ax + b > c or ax + b
- Graphing: Both linear equations and inequalities can be represented on a graph. For linear equations, the graph is a straight line, while inequalities create shaded regions on one side of the line.
Practice solving both equations and inequalities to reinforce your understanding. Start with simpler problems and gradually work your way to more complex ones. By becoming comfortable with these essential concepts, you’ll be able to tackle a variety of mathematical challenges with confidence.
Solving Quadratic Equations in Algebra
Quadratic equations are a fundamental part of mathematics, and being able to solve them is crucial for understanding more advanced topics. These equations are typically characterized by a variable raised to the second power, and solving them requires specific techniques. By mastering these methods, you can efficiently solve problems and build a strong foundation for more complex challenges.
There are several approaches for solving quadratic equations, each suited to different types of problems. Below are the most common methods used to find solutions:
- Factoring: If the quadratic equation can be factored, this is often the quickest method. Set the equation equal to zero, factor it into two binomials, and solve for the variable.
- Quadratic Formula: When factoring is difficult or not possible, the quadratic formula provides a reliable method for finding the roots. The formula is given by x = (-b ± √(b² – 4ac)) / 2a.
- Completing the Square: This method involves manipulating the equation to form a perfect square trinomial. Once this is achieved, you can take the square root of both sides to solve for the variable.
- Graphing: Quadratic equations can also be solved by graphing the equation and finding the points where the curve crosses the x-axis. These points represent the solutions to the equation.
Each method has its strengths and is appropriate for different types of quadratic equations. By practicing with various problems, you will become more proficient at recognizing which method to apply. Remember, solving these equations requires attention to detail, so take your time and carefully check each step of the process.
Graphing Techniques
Graphing is an essential skill for visualizing and solving mathematical equations. By plotting equations on a coordinate plane, you can gain a better understanding of their behavior and identify solutions more easily. There are several techniques to graph different types of equations, and each method helps to reveal key insights into the relationship between the variables.
When graphing equations, it’s important to follow a systematic approach to ensure accuracy. Whether you’re dealing with linear equations, quadratic functions, or more complex expressions, the process typically involves plotting points, determining intercepts, and understanding the general shape of the graph.
| Equation Type | Graphing Method | Key Features |
|---|---|---|
| Linear Equations | Plot two points and connect them with a straight line. | Straight line with a constant slope. |
| Quadratic Functions | Find the vertex and plot additional points symmetrically. | U-shaped curve (parabola). |
| Systems of Equations | Graph both equations and find the intersection point. | Point of intersection represents the solution. |
| Absolute Value Functions | Plot the vertex and create a V-shaped graph. | V-shaped graph with a sharp vertex. |
Mastering graphing techniques allows you to quickly interpret equations and identify key points, such as the intercepts or maximum/minimum values. Regular practice with different types of graphs will help build confidence and improve your problem-solving skills.
Examining Systems of Equations
Systems of equations involve multiple equations that are solved simultaneously. The goal is to find the values of the variables that satisfy all equations in the system. These problems are common in various fields, and understanding how to solve them efficiently is essential for progressing in mathematics.
There are different methods for solving systems of equations, each suitable for different types of problems. Below are the most widely used techniques:
- Substitution Method: In this method, you solve one equation for one variable and substitute this expression into the other equation. This allows you to solve for the second variable and then back-substitute to find the first.
- Elimination Method: The elimination method involves adding or subtracting the equations in the system to eliminate one variable. Once one variable is eliminated, solving for the remaining variable is straightforward.
- Graphing Method: You can graph each equation on a coordinate plane and find the point where the two graphs intersect. The coordinates of this intersection point are the values that satisfy both equations.
Each method has its advantages depending on the complexity of the system and the type of equations involved. For linear systems, substitution and elimination are often quicker, while the graphing method is useful for visualizing the solution. Practice with different systems will help you decide which method is best suited to each problem.
How to Avoid Common Mistakes
Mathematics can be tricky, especially when working with equations and solving problems that require multiple steps. It’s easy to make mistakes that can lead to incorrect solutions, but understanding where errors typically occur can help you avoid them. By recognizing common pitfalls, you can sharpen your problem-solving skills and become more confident in your abilities.
Some of the most frequent mistakes occur in the following areas:
- Incorrectly applying the distributive property: When expanding expressions, it’s crucial to distribute correctly. Always double-check that you are multiplying each term inside the parentheses by the factor outside.
- Sign errors: Pay careful attention to positive and negative signs. A small sign mistake, like misplacing a negative sign, can drastically change the outcome of an equation.
- Forgetting to simplify: After solving an equation or expression, always simplify your answer if possible. Leave no terms uncombined or fractions unsimplified.
- Misinterpreting word problems: Word problems often require translating real-world scenarios into mathematical expressions. Ensure you read the problem carefully and identify what each variable represents.
By practicing these tips and staying attentive to the details, you can avoid these common errors and approach problems with more confidence. Double-checking your work is always a good habit, especially when solving complex expressions or equations.
Study Methods for Success
Achieving success in mathematics requires more than just understanding formulas–it’s about consistent practice, active engagement with the material, and developing effective study habits. Knowing how to approach your learning process can make a significant difference in retaining information and solving problems efficiently.
Here are some effective study techniques to help you excel:
Active Problem-Solving
One of the most effective ways to master mathematical concepts is by actively solving problems. The more you practice, the more comfortable you become with different types of equations and functions. Focus on tackling a variety of problems, starting from the basics and progressing to more challenging ones. This builds both your skills and your confidence.
Collaborative Learning
Working with others can enhance your understanding. Group study sessions allow you to exchange ideas, solve problems together, and clarify any doubts. Explaining concepts to someone else is also a great way to reinforce your knowledge and identify any gaps in your understanding.
In addition to these methods, always make sure to review your notes regularly, break down complex topics into smaller, manageable parts, and stay consistent in your study habits. Success in mathematics is built on steady effort and persistence, so stay focused and keep practicing.
What to Expect on the Assessment
As you prepare for the upcoming assessment, it’s important to understand the key components that will be tested. This will help you focus your studies and ensure you’re well-prepared for the challenges ahead. The assessment will cover a wide range of topics, from basic problem-solving techniques to more advanced concepts that require deeper understanding.
Here’s a breakdown of what you can expect:
Types of Problems
The assessment will include a mix of problem types designed to test various mathematical skills. These may include:
- Simple equations and expressions
- Word problems requiring logical reasoning
- Graphical interpretations of functions
- Systems of equations and inequalities
- Quadratic and rational equations
Time Management
Time is a crucial factor during the assessment. Make sure to allocate enough time to review each problem carefully, but also avoid spending too much time on any single question. Efficient time management is key to completing the test successfully.
| Topic | Key Concepts | Expected Difficulty |
|---|---|---|
| Basic Equations | Solving simple linear and polynomial equations | Easy to moderate |
| Word Problems | Translating real-world situations into equations | Moderate |
| Graphing | Identifying and plotting points, interpreting functions | Moderate to challenging |
| Quadratic Equations | Solving and graphing quadratic functions | Challenging |
By understanding what to expect, you’ll be better equipped to approach each problem with confidence. Practice regularly, stay organized, and remember that time management plays an important role in your success on the test.
How to Check Your Results Effectively

After completing any set of problems, it’s essential to take the time to review your solutions. Properly checking your results can help identify mistakes, solidify your understanding, and improve accuracy. This process ensures that you don’t miss any simple errors and gives you a better chance of achieving the best possible outcome.
Here are some key strategies for verifying your work:
Step-by-Step Verification
One of the most effective methods for reviewing your work is to go through each solution step by step. Ensure that you followed all the required procedures correctly and check for any miscalculations. Pay special attention to signs, coefficients, and operations that could be easily overlooked.
Use Reverse Operations
Another powerful technique is using reverse operations to check your results. For example, if you solved for a variable, substitute the value back into the original equation to confirm it satisfies the problem. This can be especially helpful for verifying simple equations.
Estimate Your Results
If applicable, try estimating the result before solving the problem to get a rough idea of what the answer should be. If your final answer is significantly different from your estimate, this may be a sign that an error was made somewhere in the process.
Check Units and Context
In word problems or applied mathematics, always verify that your results make sense in the context of the question. Are the units correct? Does the solution fit the real-world scenario described? If anything seems off, double-check your steps for possible mistakes.
By incorporating these strategies, you can more confidently verify your work and improve the accuracy of your results. Checking your solutions thoroughly not only helps you avoid errors but also reinforces your understanding of the material.
How to Manage Time During the Test
Time management plays a crucial role in performing well on any assessment. Without a clear plan, it’s easy to feel overwhelmed and rushed, which can lead to avoidable mistakes. The key is to approach the task with a strategy that allows you to allocate enough time for each part of the test while maintaining focus and accuracy.
Here are some effective methods for managing your time during the assessment:
Prioritize the Questions
Start by scanning the entire test to get an overview of the questions. Identify the ones you feel most confident about and tackle them first. By handling easier questions early, you gain momentum and save time for more challenging ones later.
Set Time Limits
Before you start, divide the total time available by the number of sections or questions to get an idea of how much time you should spend on each one. For example, if the test is 60 minutes long and has 12 questions, aim to spend no more than 5 minutes per question. This helps you stay on track and prevents you from spending too much time on any one item.
Don’t Get Stuck on Difficult Questions
If you encounter a particularly tough problem, move on and come back to it later if time allows. Spending too much time on one question can drain your energy and make it harder to focus on the rest of the test. Keep your momentum going by sticking to your time limits.
Review the Test
Once you’ve completed the main portion of the test, take the remaining time to review your answers. Look for any careless mistakes, missing steps, or unclear calculations. If you find any errors, correct them quickly without rushing.
Practice Time Management Before the Test
To improve your time management skills, practice taking timed practice tests before the actual assessment. This will help you get used to pacing yourself, managing stress, and adjusting to the time constraints on the day of the test.
By applying these strategies, you can efficiently manage your time, reduce stress, and increase your chances of success during the test.
Review Resources for Mastery
Effective preparation is key to succeeding in any assessment. Having access to the right review materials can make a significant difference in your ability to understand complex topics and perform confidently. Here are several resources that can help you refresh your knowledge and sharpen your skills before the test.
Study Guides and Textbooks
Textbooks and comprehensive study guides often provide detailed explanations of key concepts and practice problems. These materials are structured to cover all essential topics and give you a well-rounded understanding. Consider reviewing the following:
- Chapter summaries: Focus on the end-of-chapter summaries for key concepts and formulas.
- Practice problems: Work through exercises in your textbook or study guide to reinforce what you’ve learned.
- Example problems: Revisit solved examples to understand the step-by-step approach to solving different types of questions.
Online Platforms and Tools
There are numerous websites and apps designed specifically to support learning and practice. These platforms often include video tutorials, interactive quizzes, and additional practice tests that can be invaluable in your preparation:
- Khan Academy: Offers free video lessons and practice exercises on a wide range of topics.
- Quizlet: Allows you to use flashcards and practice tests to reinforce your understanding.
- Wolfram Alpha: A computational tool that can help check your solutions and explain step-by-step solutions.
Study Groups and Tutoring
Collaborating with others can be an effective way to review difficult topics. Study groups allow you to share insights and discuss problems together, which can deepen your understanding. Alternatively, one-on-one tutoring can provide targeted support for areas where you need the most improvement.
Using a combination of these resources will give you a comprehensive review and a better chance of performing well during the assessment. Start early, and make sure to practice regularly to ensure you’re ready for any challenges that arise.