
When preparing for a major assessment in mathematics, it’s crucial to focus on the core principles and problem-solving techniques that will help you succeed. Strengthening your understanding of key topics can make a significant difference in your ability to tackle complex questions and solve them efficiently.
From working through equations to mastering different types of functions, it’s important to develop a solid foundation in all the necessary areas. Reviewing the critical concepts and practicing problems will help you improve both your speed and accuracy, ensuring you’re ready for any challenge that comes your way.
Effective preparation involves more than just memorizing formulas–it’s about understanding the logic behind them and applying this knowledge to a variety of scenarios. As you work through different types of problems, focus on honing your ability to recognize patterns and connect ideas across multiple topics.
Key Concepts for Mathematical Assessment Preparation
When it comes to preparing for a significant evaluation in mathematics, mastering the essential concepts and techniques is crucial. A strong grasp of the foundational topics will not only help in solving individual problems but also enable you to approach more complex questions with confidence. This section will highlight the major areas to focus on in your study routine.
Start by ensuring you are comfortable with basic operations and how to manipulate variables within various equations. Developing fluency in these skills will make it easier to move on to more advanced topics.
Key Areas to Focus On:
- Linear relationships and graphing techniques
- Solving quadratic equations through different methods
- Operations with polynomials and rational expressions
- Understanding and applying exponents and powers
- Mastering systems of equations and their solutions
- Working through word problems and real-world scenarios
By revisiting these fundamental ideas and practicing the necessary steps, you’ll build the confidence to handle a wide variety of questions. It’s important to practice regularly and understand the logic behind the steps, not just memorize formulas. The more you familiarize yourself with different problem types, the more intuitive solving them will become.
Additionally, focus on recognizing common patterns in equations and solutions, as this will help you navigate similar problems quickly during the test.
Essential Topics for Mathematical Preparation
To succeed in any comprehensive assessment, it’s important to focus on the foundational concepts that form the core of mathematical problem-solving. By understanding the key principles and strengthening your skills in these areas, you’ll be better equipped to tackle a wide range of questions. The following topics are crucial to your overall success.
Key Areas to Master:
- Linear Equations: Developing the ability to solve for unknowns and graph these relationships is essential.
- Quadratic Equations: Understanding the methods to solve these equations–such as factoring, completing the square, and using the quadratic formula–will be critical.
- Polynomials: Being able to perform operations like addition, subtraction, and multiplication with polynomials is foundational.
- Systems of Equations: Learning to solve systems using substitution or elimination will help you with more complex problems.
- Functions: Recognizing different types of functions and their properties, including how to interpret and graph them, is key.
Important Techniques to Practice:
- Factoring: Recognizing when and how to factor expressions can simplify many problems.
- Working with Fractions: Mastery of adding, subtracting, multiplying, and dividing rational numbers is necessary for problem-solving.
- Exponents: Understanding the rules for working with exponents, including laws of exponents and simplification techniques, is a must.
By ensuring a solid understanding of these topics and practicing the corresponding techniques, you’ll be prepared to handle a wide array of challenges. Focus on mastering each area and revisiting key problems until you feel confident in applying these strategies during your test.
Key Formulas to Memorize for the Assessment

Understanding and memorizing key formulas is essential for success in any mathematics test. These formulas serve as the foundation for solving a wide variety of problems and provide the structure needed to navigate more complex tasks. Below are some of the most important formulas that should be at the forefront of your preparation.
Core Mathematical Formulas:
- Slope Formula: m = (y₂ – y₁) / (x₂ – x₁) – Used to calculate the slope between two points on a graph.
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – Helps solve any quadratic equation in standard form.
- Point-Slope Form: y – y₁ = m(x – x₁) – A way to write the equation of a line when the slope and a point on the line are known.
- Factoring Difference of Squares: a² – b² = (a – b)(a + b) – A method for factoring expressions that are the difference between two squares.
- Sum and Difference of Cubes: a³ – b³ = (a – b)(a² + ab + b²) and a³ + b³ = (a + b)(a² – ab + b²) – Formulas used to factor cubes.
Additional Helpful Formulas:

- Pythagorean Theorem: a² + b² = c² – Used to find the length of a side of a right triangle.
- Exponential Growth/Decay Formula: y = y₀e^(kt) – Describes exponential growth or decay over time.
- Distributive Property: a(b + c) = ab + ac – Helps simplify expressions by distributing multiplication over addition or subtraction.
Memorizing these key formulas and practicing their applications will greatly enhance your ability to solve problems efficiently. Regular practice and a deep understanding of each formula’s purpose will allow you to apply them effectively during the test.
Understanding Linear Equations and Graphs
Linear equations and their graphical representations are fundamental concepts that play a key role in many mathematical problems. These equations describe relationships between variables and can be visualized as straight lines on a graph. Mastering both the algebraic manipulation of these equations and their graphical interpretation is essential for solving a wide range of questions.
To understand these equations, it’s important to recognize the form they typically take: y = mx + b, where m represents the slope of the line, and b represents the y-intercept, or the point where the line crosses the y-axis. Knowing how to identify these components allows you to quickly interpret the behavior of the line.
Graphing linear equations involves plotting points based on the equation’s solutions and connecting them to form a straight line. The slope indicates the steepness and direction of the line, while the y-intercept tells you where the line intersects the vertical axis.
By practicing with various examples, you’ll gain confidence in both writing equations from given information and graphing them accurately. Whether working with word problems or abstract equations, understanding these principles will help you approach many different types of mathematical tasks.
How to Solve Quadratic Equations
Solving quadratic equations is a crucial skill in mathematics. These equations typically involve a variable raised to the second power and may require different techniques depending on their structure. Mastering various methods for solving them will help you approach problems with confidence and efficiency.
Methods for Solving Quadratics:
- Factoring: This method works when the equation can be expressed as the product of two binomials. After factoring, set each factor equal to zero and solve for the variable.
- Completing the Square: This technique involves manipulating the equation so that one side becomes a perfect square trinomial, which can then be solved by taking the square root of both sides.
- Quadratic Formula: The general formula for solving any quadratic equation is x = (-b ± √(b² – 4ac)) / 2a. This method is reliable for all quadratic equations and helps find the roots directly.
Steps for Applying the Quadratic Formula:
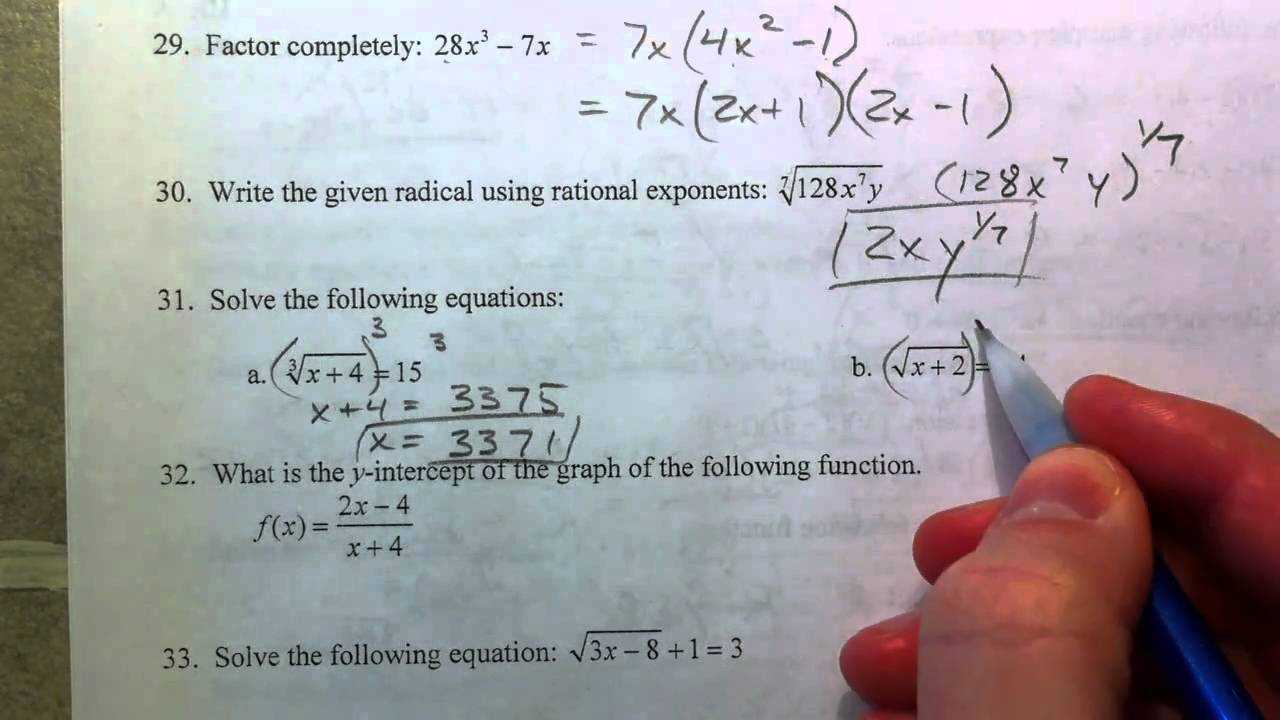
- Identify the values of a, b, and c from the equation in standard form: ax² + bx + c = 0.
- Substitute these values into the quadratic formula.
- Simplify the expression under the square root (the discriminant) and solve for x.
Each method has its advantages depending on the equation at hand. For example, factoring is quick when the equation is easily factorable, while the quadratic formula works for all types of quadratic equations, even those with no simple factors. Regular practice will help you become proficient in recognizing which method to use and applying it correctly.
Working with Rational Expressions and Equations
Rational expressions and equations involve fractions where the numerator and denominator are both polynomials. These expressions require specific techniques for simplifying, solving, and manipulating them effectively. Understanding how to work with these forms is essential for solving a variety of mathematical problems.
When simplifying rational expressions, it’s crucial to factor both the numerator and the denominator to identify common factors that can be canceled out. Solving equations that involve rational expressions often requires eliminating denominators by multiplying both sides by the least common denominator (LCD).
Key Steps in Working with Rational Expressions:
| Step | Description |
|---|---|
| 1. Factor the Numerator and Denominator | Factor both the top and bottom of the expression completely to look for common factors. |
| 2. Simplify the Expression | Cancel out any common factors between the numerator and denominator to simplify the expression. |
| 3. Eliminate Denominators in Equations | Multiply both sides of the equation by the LCD to eliminate any fractions. |
| 4. Solve the Resulting Equation | After clearing fractions, solve the resulting equation just like a regular algebraic equation. |
Working with rational equations requires careful attention to restrictions on the variable, as certain values may make the denominator zero. Always check for these values to avoid undefined solutions. With consistent practice, you will gain proficiency in manipulating and solving these types of expressions and equations.
Tips for Tackling Word Problems Effectively
Word problems can be challenging, but with the right approach, they become much more manageable. The key is breaking down the problem step by step and translating the written information into mathematical terms. By following a systematic method, you can solve even the most complex problems with confidence.
Steps to Solve Word Problems:
- Read the Problem Carefully: Take your time to understand what is being asked. Identify important information and look for key numbers, relationships, and unknowns.
- Define Variables: Assign a variable to represent the unknown quantity. This will help turn the word problem into a solvable equation.
- Translate Words into Equations: Look for phrases that indicate mathematical operations, such as “total,” “difference,” “product,” or “sum,” and write them as equations.
- Set Up the Equation: Once you have the relationships identified, create an equation that models the situation. This is often the most important step in word problems.
- Solve the Equation: Use appropriate methods to solve the equation and find the value of the variable.
- Check the Solution: Once you have a solution, go back and make sure it answers the question posed in the problem. Verify that the units and logic make sense.
Common Word Problem Strategies:
- Draw a Diagram: For problems involving geometry or movement, a visual representation can often help you understand the situation more clearly.
- Work Backwards: In some cases, it can be helpful to start with the solution and work backwards to find the unknowns.
- Use Logical Estimation: If you’re unsure about the solution, estimate the answer before solving to help you gauge if the final result makes sense.
By following these tips and practicing regularly, you will improve your ability to approach and solve word problems with confidence and accuracy. The more you practice, the easier it will become to translate words into numbers and equations.
Analyzing Functions and Their Properties
Understanding functions and their characteristics is a fundamental aspect of solving mathematical problems. A function describes the relationship between two variables, where each input corresponds to exactly one output. Analyzing these relationships allows you to uncover important features such as domain, range, intercepts, and behavior of the function.
Key Properties of Functions:
- Domain and Range: The domain refers to all possible input values, while the range represents all possible output values. Identifying the domain and range helps in understanding the limits of the function.
- Intercepts: The x-intercept is where the function crosses the x-axis, and the y-intercept is where the function crosses the y-axis. These points provide useful information about the function’s behavior.
- Increasing and Decreasing Intervals: Functions may increase or decrease over certain intervals. Identifying these intervals is key to understanding how the function behaves as the input changes.
- Symmetry: Some functions are symmetric, either with respect to the y-axis (even functions) or the origin (odd functions). Recognizing symmetry can help simplify the analysis.
- Asymptotes: An asymptote is a line that the function approaches but never touches. Vertical and horizontal asymptotes provide insight into the function’s behavior at extreme values of the input.
Methods for Analyzing Functions:
- Graphing: Plotting a function helps visualize its key features, including intercepts, increasing/decreasing intervals, and any asymptotes.
- Identifying Patterns: Analyzing the form of the function can help predict its behavior. For example, quadratic functions have a parabolic shape, while linear functions create straight lines.
- Calculus Tools: Using derivatives and integrals allows you to examine more advanced properties of functions, such as rates of change and accumulated areas under curves.
By carefully analyzing functions, you can uncover important properties that aid in solving problems and understanding the relationships between variables. Mastering these concepts is essential for approaching more complex mathematical challenges.
Solving Systems of Equations Easily

Systems of equations involve finding the values of variables that satisfy multiple equations simultaneously. Solving these systems is a crucial skill, and there are various methods to tackle them effectively. Understanding and applying the right technique can make the process much simpler and more intuitive.
Methods for Solving Systems:
- Substitution Method: In this approach, you solve one equation for one variable and then substitute that expression into the other equation. This method is especially useful when one equation is easy to isolate a variable.
- Elimination Method: This method involves adding or subtracting the equations to eliminate one of the variables. It works best when the coefficients of one variable are opposites or can be made to be opposites.
- Graphing Method: By graphing both equations on the same coordinate plane, the solution is the point where the two lines intersect. While this method is visual, it’s less precise unless the intersection is clearly marked on the graph.
Step-by-Step Approach:
- Step 1: Choose the Method: Decide whether substitution, elimination, or graphing is the most efficient method for the system you’re working with.
- Step 2: Simplify the Equations: Ensure that both equations are in a simple form, with variables clearly on one side and constants on the other.
- Step 3: Solve for One Variable: Whether you’re using substitution or elimination, isolate one variable and solve for its value.
- Step 4: Substitute and Solve: If using substitution, substitute the value you found into the other equation. If using elimination, add or subtract the equations to eliminate one variable and solve for the other.
- Step 5: Verify the Solution: Once you have a solution, plug it back into the original equations to ensure it satisfies both equations.
By practicing these methods and understanding when to apply each one, you can solve systems of equations more easily and efficiently. The key is to choose the right approach for the problem and stay organized throughout the process.
Important Concepts in Exponents and Polynomials
Exponents and polynomials are key elements in understanding more complex mathematical relationships. These concepts form the foundation for operations involving powers of numbers and expressions with multiple terms. Mastering these ideas allows you to simplify expressions, solve equations, and work efficiently with algebraic structures.
Key Ideas in Exponents:
- Product of Powers: When multiplying two powers with the same base, add the exponents. For example, am × an = am+n.
- Power of a Power: When raising a power to another power, multiply the exponents. For example, (am)n = am×n.
- Zero Exponent: Any nonzero number raised to the power of zero equals one. For example, a0 = 1.
- Negative Exponent: A negative exponent means the reciprocal of the base raised to the positive exponent. For example, a-n = 1/an.
Key Ideas in Polynomials:
- Terms and Degree: A polynomial is made up of terms, each consisting of a coefficient and a variable raised to an exponent. The degree of the polynomial is the highest exponent of the variable.
- Adding and Subtracting Polynomials: Combine like terms by adding or subtracting their coefficients. For example, (3x2 + 4x) + (5x2 – 2x) = 8x2 + 2x.
- Multiplying Polynomials: Multiply each term in one polynomial by each term in the other. Use the distributive property (FOIL method) for binomials.
- Factoring Polynomials: Breaking down a polynomial into simpler terms, called factors, can simplify solving equations or understanding the structure of the expression.
Understanding these concepts will allow you to work with a variety of problems involving powers and expressions. Mastery of exponents and polynomials is essential for progressing to more advanced mathematical topics and problem-solving techniques.
Reviewing Inequalities and Their Solutions
Inequalities represent relationships between expressions that are not equal but instead have a range of possible values. Solving inequalities involves finding the set of values that satisfy the given condition. Understanding the properties and methods for solving inequalities is crucial for solving real-world problems and working with complex expressions.
When solving inequalities, it’s important to remember that the solutions are often ranges of values rather than single numbers. These solutions can be represented on a number line or expressed as intervals. Depending on the inequality type, different methods are used, including graphing, algebraic manipulation, and testing solutions.
In many cases, when multiplying or dividing by a negative number, the inequality symbol must be flipped. This is a key step in ensuring that the solution is accurate. Understanding this rule, along with the basic operations and properties, allows for effective and accurate solving of inequalities.
Graphing and Interpreting Absolute Value Functions
Absolute value functions describe relationships where the output is always non-negative, regardless of the sign of the input. These functions create a distinctive “V” shaped graph, where the vertex represents the minimum or maximum value depending on the orientation. Understanding how to graph these functions and interpret their meaning is an essential skill for analyzing real-world scenarios.
Graphing Absolute Value Functions:
To graph an absolute value function, start by identifying the vertex, which is the point where the direction of the graph changes. This point is typically where the expression inside the absolute value equals zero. From the vertex, the graph extends symmetrically in both directions, creating the characteristic V-shape. The slope of the lines on either side of the vertex depends on the coefficient of the absolute value expression.
- Example 1: For the function f(x) = |x – 3|, the vertex is at (3, 0), and the graph opens upwards.
- Example 2: For the function f(x) = -|x + 2| + 4, the vertex is at (-2, 4), and the graph opens downwards.
Interpreting the Graph:
When interpreting absolute value functions, the key is understanding how the transformations affect the graph. A vertical shift moves the graph up or down, while a horizontal shift moves it left or right. The coefficient in front of the absolute value affects the steepness of the graph and whether it opens upwards or downwards.
- Vertical shift: Adding or subtracting a constant to the entire function moves the graph up or down.
- Horizontal shift: Adding or subtracting a value inside the absolute value expression shifts the graph left or right.
- Reflection: A negative coefficient in front of the absolute value causes the graph to flip, opening in the opposite direction.
By mastering the graphing and interpretation of absolute value functions, you can analyze various real-world problems that involve distances, errors, and differences, where only the magnitude of values matters, not their direction.
Understanding Slope and Y-Intercept
The slope and y-intercept are key components in understanding linear relationships. The slope indicates how steep a line is, while the y-intercept reveals where the line crosses the vertical axis. These two values provide essential information about the direction and position of a line on a graph. By understanding their significance, you can easily interpret and manipulate linear equations in a variety of contexts.
What is Slope?
Slope represents the rate of change between two points on a line. It measures how much the value of the output (y) changes relative to a change in the input (x). In simple terms, slope tells you how much the line rises or falls as you move from left to right. Mathematically, slope is often written as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
- Positive slope: A line with a positive slope rises as it moves from left to right.
- Negative slope: A line with a negative slope falls as it moves from left to right.
- Zero slope: A horizontal line has a slope of zero.
- Undefined slope: A vertical line has an undefined slope.
What is Y-Intercept?
The y-intercept is the point where a line crosses the vertical axis. This value represents the output (y-value) when the input (x-value) is zero. In the equation of a line, the y-intercept is typically the constant term. It provides a starting point for the graph and helps to determine the position of the line relative to the axis.
- Interpretation: If the y-intercept is positive, the line crosses above the origin. If it’s negative, the line crosses below the origin.
- Graphing: Knowing the y-intercept allows you to plot a point on the vertical axis, giving you a reference for drawing the line.
By combining the slope and y-intercept, you can graph any linear equation and understand the relationship between the two variables it represents. These concepts are fundamental for analyzing trends, making predictions, and solving problems in a wide range of fields.
Factoring Strategies for Complex Problems
Factoring is a powerful tool for simplifying expressions and solving equations. While some problems may seem daunting at first glance, breaking them down into manageable parts can make the process much easier. By using a few key strategies, you can factor even the most complicated expressions effectively. These techniques focus on recognizing patterns, applying basic rules, and transforming equations into forms that are easier to work with.
One of the most effective methods is factoring by grouping, where terms are paired in such a way that common factors can be extracted from each group. Another useful strategy is recognizing special product formulas, like the difference of squares or perfect square trinomials, which simplify factoring significantly. Moreover, mastering the quadratic formula and the process of splitting the middle term can also help handle more complex expressions efficiently.
In many cases, the goal is to break down a complex expression into simpler factors that can be solved or simplified further. By practicing these techniques and understanding the underlying principles, you can tackle even the toughest factoring problems with confidence and accuracy.
Mastering Operations with Rational Numbers
Understanding how to manipulate rational numbers is a fundamental skill in mathematics. Whether adding, subtracting, multiplying, or dividing fractions, mastering these operations ensures a strong foundation for more advanced topics. By breaking down the steps and practicing various methods, you can improve your ability to handle fractions and rational expressions with ease.
To add or subtract fractions, it is essential to have a common denominator. This allows the fractions to be combined easily. For multiplication and division, understanding how to multiply numerators and denominators, as well as how to simplify expressions, is crucial. Dividing fractions, though often tricky, follows a simple rule of flipping the second fraction and then multiplying.
| Operation | Example | Result |
|---|---|---|
| Addition | 1/3 + 2/3 | 3/3 or 1 |
| Subtraction | 5/6 – 1/3 | 1/2 |
| Multiplication | 3/4 × 2/5 | 6/20 or 3/10 |
| Division | 3/4 ÷ 2/5 | 15/8 |
By consistently applying these principles and practicing different problems, you will develop a solid understanding of rational number operations, laying the groundwork for tackling more complex mathematical challenges.
Common Mistakes to Avoid During the Exam
When facing an assessment, it is easy to make simple errors that can cost valuable points. Understanding the most frequent mistakes and learning how to avoid them can help ensure better performance. In this section, we will discuss common pitfalls and offer advice on how to stay on track during your assessment.
- Rushing Through Problems: One of the most common mistakes is hurrying through questions without taking the time to carefully read and understand the problem. Always ensure you fully comprehend what is being asked before attempting to solve it.
- Neglecting to Check Work: Failing to double-check your answers can lead to small mistakes that are easy to overlook. Always leave time at the end to review your work and verify your solutions.
- Misapplying Formulas: It’s easy to forget the correct formulas or apply them incorrectly. Make sure you are using the right method for each type of problem and remember to review key concepts before the assessment.
- Skipping Steps: Avoid skipping steps, even if you feel confident. Writing out every step not only ensures accuracy but also helps you track where things went wrong if you get an incorrect result.
- Overlooking Negative Signs: Negative signs are crucial in many calculations. Be cautious with adding and subtracting negative numbers to prevent errors that could change the outcome of your solution.
By staying mindful of these potential mistakes, you can approach your tasks more strategically and reduce the chances of losing points on easily avoidable errors. Always take your time, stay organized, and approach each problem methodically.
Effective Study Strategies for Exam Success
Achieving success on any assessment requires more than just reviewing notes; it demands a strategic approach to studying. Effective preparation involves organizing your time, using the right techniques, and focusing on understanding rather than memorization. This section provides key strategies to help you study efficiently and perform at your best.
Time Management and Planning
One of the most important aspects of preparation is creating a structured study plan. Allocate sufficient time to each topic and ensure you start well in advance to avoid last-minute cramming. Breaking down study sessions into focused intervals can help improve retention and reduce stress.
- Use a Study Schedule: Organize your study time by planning what you need to cover each day, and be sure to stick to the schedule.
- Prioritize Difficult Topics: Focus on areas where you feel less confident or where you tend to make mistakes.
- Take Regular Breaks: Short, frequent breaks can help maintain focus and prevent burnout.
Active Learning Techniques
Instead of passively reading through your notes, engage with the material using active learning methods. This not only strengthens your understanding but also improves long-term retention.
- Practice Problems: Consistently solving problems allows you to apply concepts and identify areas that need more attention.
- Teach Someone Else: Explaining concepts to a peer is an excellent way to reinforce your knowledge.
- Use Flashcards: Flashcards are an effective way to test your memory and reinforce key concepts.
Utilizing Available Resources
Don’t limit your study efforts to only textbooks. There are many resources available to reinforce your learning.
- Online Resources: Platforms offering practice questions, explanations, and tutorials can provide valuable support.
- Study Groups: Collaborating with others can offer different perspectives and help clarify confusing topics.
- Past Tests: Reviewing previous tests or practice papers is one of the most effective ways to understand the format and types of questions you might encounter.
| Study Strategy | Benefit |
|---|---|
| Time Management | Reduces stress, ensures coverage of all topics |
| Active Learning | Improves retention and understanding |
| Using Resources | Provides additional practice and perspectives |
By incorporating these strategies into your study routine, you can approach your preparation with confidence and ensure a greater chance of success. Always stay consistent, focused, and proactive in your approach.