
In this section, we will explore essential problem-solving techniques and strategies that can help students grasp the core ideas of introductory mathematics. The focus is on developing a deep understanding of the fundamental principles that form the basis for more advanced studies. Whether you’re tackling simple equations or more complex expressions, building a strong foundation is crucial.
Step-by-step solutions and practical examples will guide you through common challenges, ensuring that you not only arrive at the correct results but also understand the reasoning behind each step. With a variety of methods at your disposal, you’ll be equipped to handle a wide range of mathematical problems.
By mastering these core techniques, students will gain confidence and improve their ability to approach future lessons with a clearer perspective. Each problem is an opportunity to apply critical thinking skills and refine your approach to learning.
Algebra 1 Florida Textbook Answers

In this section, we provide detailed solutions to various problems encountered in introductory mathematics courses. These solutions are designed to enhance your understanding by breaking down each problem into manageable steps. With a focus on clarity and logic, these methods can help students navigate even the most challenging exercises.
By working through these examples, you’ll gain insight into solving equations, manipulating variables, and applying mathematical rules effectively. Each solution is explained thoroughly, ensuring that you not only reach the correct result but also understand the reasoning behind each step. Practice is key in mastering these skills, and by following the outlined processes, you’ll be prepared for more complex concepts in the future.
Additionally, these exercises encourage students to develop problem-solving strategies that can be applied to a variety of mathematical contexts. Understanding the patterns and techniques used in solving problems will improve your ability to approach similar tasks with confidence, making future learning more intuitive and less daunting.
Key Concepts in Algebra 1
This section focuses on the fundamental principles that form the foundation of early mathematical learning. Understanding these key concepts is essential for developing the skills needed to solve equations and analyze relationships between variables. Whether you’re just beginning or looking to strengthen your knowledge, mastering these ideas is crucial for academic success.
Understanding Variables and Expressions
At the core of many mathematical problems are variables, which represent unknown values. Expressions combine variables with constants and operators, forming the basis for equations and inequalities. Knowing how to manipulate and simplify these expressions is a critical skill for solving problems and working with mathematical relationships. Recognizing patterns in these expressions allows you to predict outcomes and create more complex models.
Solving Equations and Inequalities

Solving equations is a fundamental part of learning mathematics. It involves finding the value of a variable that satisfies the equation. Inequalities, on the other hand, express relationships where values can be greater or less than a given number. Both require a solid understanding of operations and the ability to manipulate terms correctly. By practicing these concepts, you’ll gain the ability to handle more advanced problems with ease.
Understanding the Structure of Algebra 1
The structure of an introductory mathematics course is carefully designed to build on each concept progressively. A solid understanding of the course structure helps students grasp the material more efficiently and apply what they’ve learned to more complex topics. This section will break down the key components that make up the learning path and explain how each section contributes to your overall success.
- Equations and Variables: The foundation of the course starts with understanding how variables and constants interact within equations.
- Expressions and Operations: Learning how to manipulate expressions using arithmetic operations is a vital skill for solving problems.
- Functions and Graphs: Functions describe the relationship between variables, and graphing allows you to visualize these relationships.
- Inequalities: A critical concept where values are compared and solved based on greater than, less than, or equal to conditions.
By focusing on these components, students will gain a clear understanding of the course flow and how different topics interconnect. This approach not only improves comprehension but also enhances problem-solving abilities, allowing for smoother transitions to more advanced material.
Step-by-Step Solutions for Algebra 1 Problems
In this section, we will guide you through solving common mathematical problems using a step-by-step approach. Breaking down complex problems into smaller, manageable parts is key to understanding the underlying concepts and mastering the necessary skills. Each solution will be explained thoroughly, ensuring that you can follow along and apply the same methods to similar challenges.
Starting with the basics, we will focus on how to approach each type of problem systematically. By isolating variables, simplifying expressions, and using logical operations, we will show how each step leads to the correct solution. This process not only helps solve individual problems but also builds a deeper understanding of the mathematical principles involved.
By practicing these step-by-step solutions regularly, you will develop the confidence to tackle more advanced topics and improve your problem-solving abilities. Whether dealing with equations, inequalities, or expressions, the goal is to create a solid foundation that will support future learning and application of mathematical concepts.
Common Mistakes in Algebra 1
Many students encounter similar challenges when learning the basics of mathematics. These common errors can prevent you from fully understanding the concepts and achieving success in problem-solving. In this section, we will highlight some of the most frequent mistakes and provide tips on how to avoid them. Recognizing and correcting these errors will improve your accuracy and confidence in handling mathematical tasks.
| Common Mistake | How to Avoid It |
|---|---|
| Misinterpreting negative signs | Always carefully follow the order of operations and double-check your signs, especially when working with subtraction or negative numbers. |
| Forgetting to distribute terms | When dealing with parentheses, make sure to distribute each term to avoid leaving out any factors. |
| Incorrectly solving for variables | Take your time when isolating variables, and ensure each step is logically sound before moving forward. |
| Overcomplicating simple problems | Stay calm and focus on simplifying each expression or equation step by step. Avoid rushing through the process. |
By being aware of these common mistakes and practicing proper techniques, you will improve your mathematical skills and minimize errors in future problems. Mastery comes through careful attention and consistent practice, so don’t hesitate to revisit basic concepts whenever needed.
How to Solve Linear Equations
Solving linear equations is a fundamental skill in mathematics that involves finding the value of an unknown variable. The process requires a series of logical steps to simplify the equation until the variable is isolated. Once you understand the method, solving these types of problems becomes a straightforward task that can be applied to a wide range of mathematical situations.
Step 1: Isolate the Variable
The first step in solving a linear equation is to isolate the variable on one side of the equation. This often involves performing inverse operations, such as addition, subtraction, multiplication, or division, to eliminate constants or coefficients. The goal is to simplify the equation to the form where the variable is alone on one side.
Step 2: Simplify and Solve
Once the variable is isolated, perform any remaining operations to simplify the equation and solve for the variable. This may involve combining like terms or further simplifying both sides of the equation. Always double-check your work to ensure no steps were missed and the final solution is correct.
By following these steps, you can confidently solve linear equations and apply the same approach to more complex mathematical problems in the future.
Quadratic Equations Explained
Quadratic equations are a specific type of mathematical expression that involves a variable raised to the second power. These equations can describe a wide range of real-world scenarios, from projectile motion to financial models. Solving them often requires a deeper understanding of the relationships between the variable and its coefficients, and there are several methods available to find the solution.
One common approach to solving quadratic equations is factoring, where you express the equation as a product of binomials. Another method is using the quadratic formula, which provides a general solution for any quadratic equation. Additionally, completing the square is another technique that can simplify the process and help you arrive at the correct solution.
Understanding these methods and when to apply them will give you the tools to tackle more complex problems and broaden your mathematical skills. Whether you are solving equations by factoring or using the quadratic formula, mastering these techniques is essential for progressing in mathematics.
Graphing Techniques for Algebra 1

Graphing is an essential skill in mathematics that allows you to visually represent relationships between variables. By plotting points on a coordinate plane and understanding how to draw lines and curves, you can gain valuable insights into the behavior of functions and equations. This section explores key techniques that help simplify the process and improve your graphing skills.
Plotting Points and Understanding the Coordinate Plane

Before you can graph any equation, it’s important to understand the coordinate plane. The plane consists of two axes: the horizontal x-axis and the vertical y-axis. The intersection of these axes is called the origin. Points are represented by ordered pairs (x, y), where the first number corresponds to the position on the x-axis and the second number corresponds to the position on the y-axis.
Graphing Lines and Curves
Once you’re comfortable plotting points, you can begin graphing lines and curves. Linear equations result in straight lines, while other types of equations may produce curves such as parabolas or circles. Understanding the slope and intercepts of equations is key to drawing accurate graphs. The slope represents the rate of change, and the intercepts indicate where the graph crosses the axes.
| Equation Type | Graph Shape | Key Feature |
|---|---|---|
| Linear Equation | Straight Line | Constant slope |
| Quadratic Equation | Parabola | Symmetry about the vertex |
| Circular Equation | Circle | Equal distance from the center |
By mastering these techniques, you can efficiently graph various types of equations and visualize how changes in the equation affect the graph. This skill is crucial not only for solving problems but also for interpreting real-world data and making predictions.
Using Algebra 1 for Real-World Problems
Mathematical concepts are not just abstract ideas; they can be powerful tools for solving practical problems in everyday life. By applying foundational principles, you can address a wide range of real-world challenges, from budgeting and planning to analyzing trends and making informed decisions. Understanding how to use these techniques in practical situations helps bridge the gap between theory and application.
One common way these methods are applied is in problem-solving scenarios such as calculating expenses, determining rates of change, or optimizing resources. For example, you may need to calculate the cost of materials based on unit prices or predict the future value of an investment. These types of problems are solved using the same techniques learned in a mathematical context but tailored to real-world situations.
By practicing how to translate real-world situations into mathematical equations and solving them step by step, you can develop critical thinking skills and enhance your ability to make decisions based on data and analysis. Whether in business, engineering, or daily life, the skills learned from solving mathematical problems are invaluable tools for navigating various challenges.
How to Factor Algebraic Expressions

Factoring is a key technique in simplifying mathematical expressions and solving equations. The goal is to break down a complex expression into simpler components, which can make problem-solving more efficient and help identify solutions more easily. Understanding how to factor expressions correctly is essential for progressing in various mathematical tasks, from solving quadratic equations to simplifying polynomials.
Step 1: Identify Common Factors

The first step in factoring any expression is to look for common factors among all the terms. This involves finding the greatest common divisor (GCD) of the coefficients and factoring out any shared variables or constants. Once the common factor is identified, it can be factored out to simplify the expression.
Step 2: Use Special Factoring Techniques
For more complex expressions, special factoring methods can be used. These techniques include factoring by grouping, using the difference of squares, or factoring trinomials. Each of these methods involves recognizing specific patterns and applying known formulas to simplify the expression further.
By practicing these factoring techniques, you’ll gain a deeper understanding of mathematical structures and improve your ability to solve more advanced problems with ease.
Mastering Word Problems in Algebra
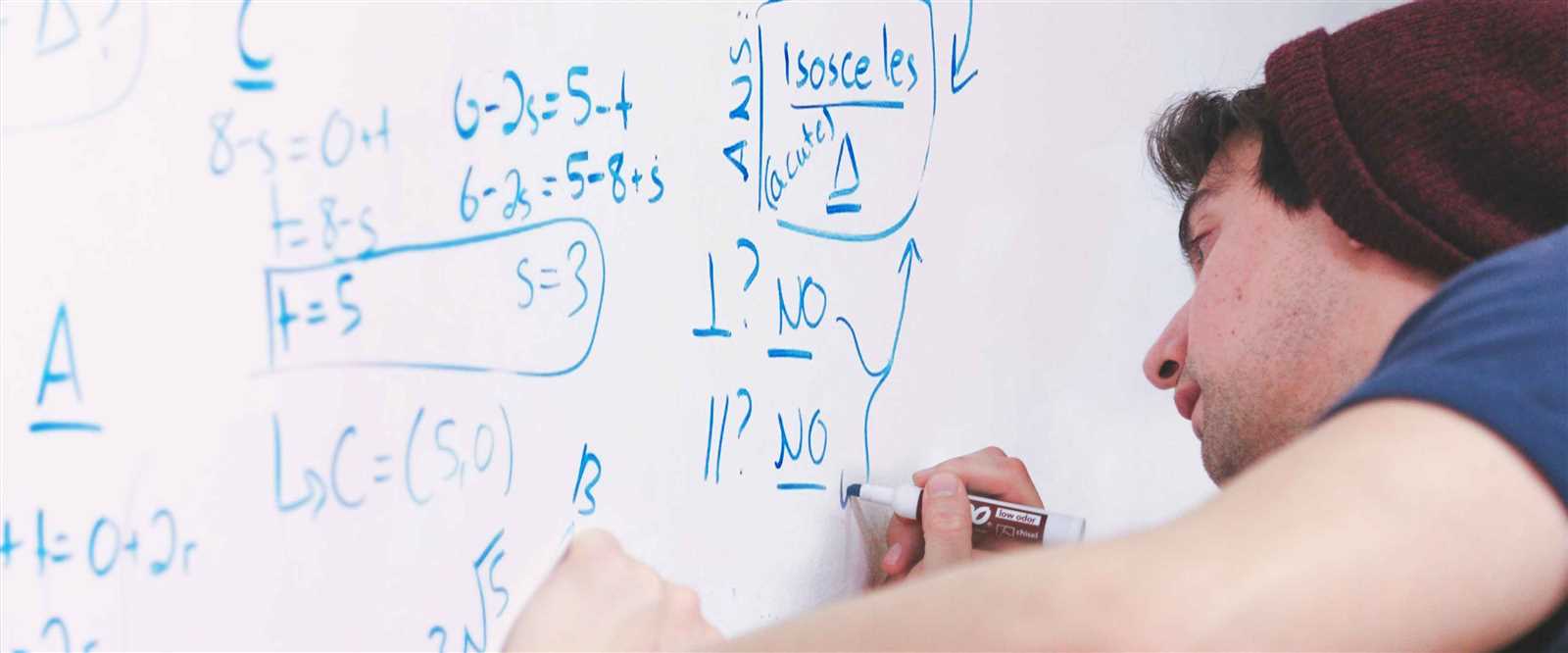
Word problems are one of the most practical applications of mathematical concepts, transforming abstract equations into real-life situations. The challenge lies in interpreting the problem correctly, identifying the relevant information, and translating it into a mathematical form that can be solved. Mastering this skill is crucial for effectively using mathematics in everyday decision-making and problem-solving.
The key to solving word problems is breaking down the information step by step. Start by carefully reading the problem and highlighting the important details. Then, determine what the unknowns are and how they relate to the information provided. Once you’ve set up the equation, use appropriate methods to solve it and check your answer in the context of the original problem.
With practice, you will become more adept at recognizing the patterns within word problems, allowing you to approach them with confidence. Remember, the more you practice, the more intuitive these problems become, and the better you’ll be at applying your mathematical knowledge to solve practical challenges.
Polynomials and Their Applications
Polynomials are a fundamental class of expressions in mathematics that can represent a wide variety of real-world phenomena. These expressions are made up of terms that include variables raised to different powers, along with coefficients. By studying polynomials, we can model and solve problems in fields ranging from physics and engineering to economics and biology.
Understanding the structure and behavior of polynomials allows us to apply them in practical ways. From determining areas and volumes to predicting trends and optimizing processes, polynomials serve as powerful tools for problem-solving. The flexibility of polynomials makes them suitable for a wide range of applications, including:
- Modeling population growth or decay over time
- Analyzing the motion of objects in physics
- Optimizing profit and cost functions in business
- Solving geometric problems involving areas and volumes
By mastering polynomials, you can tackle complex problems by breaking them down into simpler steps. This helps simplify real-world challenges and offers valuable solutions in various scientific and practical contexts.
Understanding Functions in Algebra 1
Functions are one of the most important concepts in mathematics, representing relationships between two sets of numbers or variables. A function assigns exactly one output for each input, establishing a clear rule that connects the two. Understanding how functions work is essential for solving equations, modeling real-world scenarios, and analyzing data in various disciplines.
In mathematics, functions are often expressed as equations, graphs, or tables. By recognizing the patterns and behavior of a function, you can predict outcomes, solve for unknowns, and make informed decisions. Some of the key concepts related to functions include:
- Domain and Range: The set of all possible inputs (domain) and the set of all possible outputs (range).
- Linear Functions: Functions that produce straight-line graphs, representing constant rates of change.
- Quadratic Functions: Functions that produce parabolic graphs, typically used to model acceleration or growth patterns.
- Piecewise Functions: Functions that are defined by different expressions depending on the value of the input.
By studying these concepts and how they interact, you will be able to solve more complex mathematical problems and apply the knowledge to real-life situations, such as calculating costs, predicting trends, or analyzing patterns in various fields.
Solving Systems of Equations
Solving systems of equations involves finding the values of variables that satisfy multiple equations at the same time. This is a common problem in mathematics, as many real-world situations require solving for unknowns in more than one equation. Whether in business, physics, or economics, understanding how to solve such systems is crucial for analyzing and solving complex problems.
There are several methods for solving systems of equations, each suited to different types of problems. The most commonly used methods include:
- Substitution Method: Solving one equation for a variable and then substituting that expression into the other equation.
- Elimination Method: Adding or subtracting the equations to eliminate one of the variables, making it easier to solve for the remaining variable.
- Graphical Method: Plotting both equations on a graph and finding the point of intersection, which represents the solution to the system.
By mastering these techniques, you can approach a variety of problems and find solutions with precision. With practice, solving systems of equations becomes a powerful tool for problem-solving in many fields.
Tips for Preparing for Algebra 1 Exams
Preparing for exams in mathematics requires a combination of understanding the material, practicing problem-solving techniques, and mastering test-taking strategies. With the right approach, you can confidently tackle the challenges presented in your exam and perform to the best of your ability. Below are several practical tips to help you get ready for your exam:
Understand Key Concepts
Ensure you fully grasp the main principles and methods covered in your coursework. Focus on core topics such as solving equations, graphing functions, and working with expressions. Mastery of these concepts will be essential for solving more complex problems during the exam.
Practice Regularly

Consistent practice is one of the most effective ways to prepare. Work through practice problems, sample questions, and past exams to build confidence and reinforce your understanding of the material.
| Strategy | Benefit |
|---|---|
| Practice with Timed Mock Exams | Improves time management and builds exam stamina |
| Review Mistakes Thoroughly | Helps identify weak areas and prevent future errors |
| Study in Small Chunks | Prevents burnout and improves focus |
By following these tips, you can approach your exam with confidence, knowing you’re well-prepared for the challenges ahead. Time management, consistent practice, and a solid understanding of the material will help you achieve success.
Common Algebra 1 Test Questions
When preparing for exams, it’s important to be familiar with the types of questions that are commonly asked. These questions often test key skills like simplifying expressions, solving for variables, and understanding mathematical relationships. Below are some examples of the most frequent question types you may encounter during your exam.
- Solving Linear Equations: Questions that ask you to isolate a variable and find its value.
- Graphing Functions: These questions may require you to plot a given equation or interpret a graph.
- Working with Polynomials: Expect questions about adding, subtracting, and multiplying polynomials.
- Factoring Expressions: You might be asked to factor quadratic expressions or simplify complex binomials.
- Simplifying Rational Expressions: These questions test your ability to reduce fractions and rationalize denominators.
- Word Problems: Many exams include practical scenarios where you must apply mathematical methods to solve real-world problems.
Familiarizing yourself with these common question types will help you feel more prepared and confident. Practice solving these problems ahead of time, so you can approach the test with ease.
How to Use Online Resources for Algebra
In today’s digital age, there are many online tools and resources available to help students master mathematical concepts. These resources provide a variety of learning methods, from interactive tutorials to video lessons and practice problems. Using these tools effectively can significantly enhance your understanding of mathematical topics and improve your problem-solving skills.
Here are some tips for utilizing online resources:
- Interactive Problem Solvers: Many websites offer step-by-step guides to solving various types of equations. These tools can help you learn the process of solving problems at your own pace, providing instant feedback along the way.
- Video Tutorials: Platforms like YouTube and educational websites often feature videos that break down complex topics into easy-to-understand lessons. Watching these can reinforce what you’ve learned in class and offer new perspectives.
- Online Practice Exercises: Practice makes perfect. Many websites provide a wide range of practice questions, from basic to advanced, allowing you to test your skills and track your progress.
- Forums and Discussion Groups: Joining online math forums or study groups can help you connect with peers and experts who can assist with difficult concepts. You can ask questions, share strategies, and learn from others’ experiences.
By leveraging these online tools, you can make your learning experience more interactive and effective, building confidence as you tackle different mathematical challenges.