
As the examination period approaches, students often seek reliable guidance to tackle the key topics that will be covered. Mastering the essential principles is crucial for success, and understanding the structure of the assessment can make a significant difference in how well you perform. This section focuses on strategies to enhance your preparation and ensure a solid grasp of the material.
Effective study techniques are just as important as the content itself. Knowing where to focus your energy can help you identify the areas that require the most attention, while also reinforcing your strengths. The more familiar you are with the test format and its demands, the better prepared you’ll be on the day of the exam.
Confidence in your knowledge and problem-solving skills is key. By reviewing practice questions and understanding the core methods, you can approach the exam with a clear strategy and a calm mindset. With the right approach, achieving success becomes more than just a possibility–it becomes a certainty.
Algebra 1 Exam Preparation Tips

Preparing for an important test requires a systematic approach and careful planning. It’s not just about knowing the material but also about managing your time and setting the right mindset. Success often comes down to consistency and focusing on the most critical areas that will be tested. Below are key strategies to help you get ready effectively and efficiently.
Effective Study Habits
To ensure solid preparation, develop a study routine that you can stick to. Consistency is key, as cramming at the last minute is rarely effective. Break down your study sessions into manageable blocks, focusing on one topic at a time. This approach helps to build a deeper understanding and reduces stress.
| Study Method | Benefits |
|---|---|
| Practice Problems | Improves problem-solving skills and identifies weak areas |
| Flashcards | Helps with memorizing key formulas and concepts |
| Group Study | Allows sharing different perspectives and explanations |
| Online Resources | Provides additional practice questions and tutorials |
Test-Taking Strategies
When it comes to the actual exam, knowing how to approach the questions is just as important as knowing the answers. Start by reviewing the instructions carefully and managing your time wisely. Skip difficult questions initially and return to them later when you have more time. Stay calm and focus on applying your knowledge step by step.
Key Topics Covered in Algebra 1 Exam

Understanding the core concepts and topics is crucial for success in any examination. The areas that are most commonly tested are those that form the foundation of mathematical problem-solving. A strong grasp of these essential subjects will help you approach the test with confidence and precision. Below are the key areas that you should focus on during your preparation.
Solving Equations and Inequalities
One of the most important skills is solving both linear equations and inequalities. These problems require you to find the value of the unknown variable through a series of logical steps. Practice solving simple to complex equations, and make sure you understand the principles behind balancing both sides of the equation.
Functions and Their Properties
Understanding functions is another critical topic. This includes identifying, interpreting, and graphing different types of functions such as linear, quadratic, and exponential. You should also be familiar with function notation and how to evaluate functions for specific values of the variable.
Understanding the Exam Structure
Knowing how the exam is organized is just as important as understanding the material itself. A well-structured test is designed to evaluate your understanding of key concepts and how well you can apply them in different scenarios. Familiarizing yourself with the exam layout allows you to approach each section with confidence and use your time effectively.
Types of Questions

The exam typically consists of a variety of question types, including multiple-choice, short answer, and problem-solving exercises. Multiple-choice questions are designed to test your recognition of correct answers and concepts, while short-answer and problem-solving questions require you to demonstrate your reasoning and process step by step. Understanding the format of each question type is crucial for effective preparation.
Time Allocation and Strategy
Time management plays a significant role in performing well on the exam. Each section is usually allotted a specific amount of time, and managing that time wisely can make a big difference. Prioritize easier questions first and return to more difficult ones once you’ve completed the rest. Practicing under timed conditions can help you get comfortable with this strategy.
How to Find Correct Exam Solutions
Finding reliable solutions to practice problems is an essential part of preparing for any major exam. It’s important to have access to accurate resources that not only provide the correct answers but also explain the reasoning behind them. This section will guide you through various strategies and resources that can help you identify and understand the solutions.
Utilizing Online Resources
The internet offers a wide range of platforms with practice exercises and solutions that can help solidify your understanding. Some websites and educational platforms provide step-by-step explanations, which are useful for understanding how to approach each question. When searching for solutions, make sure to use trusted sources.
- Educational websites with tutorial sections
- Interactive learning platforms offering practice quizzes
- YouTube channels that explain common problems and solutions
Using Study Guides and Textbooks

Textbooks and study guides are great for reviewing and verifying your answers. They not only offer solutions but often include explanations and examples that can help you learn how to solve similar problems in the future. Make use of any review sheets or example problems provided by your course material.
- Review chapter summaries and practice problems in textbooks
- Use answer keys provided in study guides for additional practice
- Focus on example questions from past exams or practice tests
Effective Study Strategies for Success
To perform well on any challenging exam, it’s important to adopt efficient study habits. Preparation goes beyond simply reading through notes; it requires active engagement with the material and a systematic approach. The following strategies can help you maximize your study time and improve retention, making your exam preparation more effective.
Active Learning Techniques
Instead of passively reviewing your notes, try to engage with the material through active learning techniques. This involves solving practice problems, summarizing key concepts in your own words, and teaching what you’ve learned to someone else. These methods help reinforce your understanding and identify areas that need further review.
- Work through a variety of practice exercises
- Explain concepts aloud to reinforce your understanding
- Use mind maps or diagrams to visualize complex ideas
Time Management and Consistency
Consistency is crucial when preparing for an exam. Rather than cramming the night before, break your study sessions into focused intervals over several weeks. Use a schedule or study plan to ensure you cover all necessary topics. Allocate more time to areas where you feel less confident, but also make sure to review your strengths periodically.
- Set specific study goals for each session
- Use the Pomodoro technique for focused study periods
- Track your progress to stay motivated and on schedule
Common Mistakes to Avoid During the Exam
When preparing for a major test, it’s just as important to avoid common errors as it is to master the material. Many students make mistakes due to carelessness, lack of understanding, or improper time management. By recognizing these pitfalls and actively working to avoid them, you can greatly improve your performance on the exam.
| Mistake | Why It Happens | How to Avoid It |
|---|---|---|
| Rushing Through Questions | Panic or poor time management | Take your time, read questions carefully, and double-check your work |
| Skipping Difficult Problems | Fear of not knowing the answer | Attempt all questions, move on and return to tough ones later |
| Not Showing Work | Lack of attention to detail | Write out every step, even if you can solve the problem mentally |
| Misinterpreting the Question | Not fully understanding what is being asked | Pay close attention to key words and phrases in each question |
| Overlooking Simple Errors | Not reviewing answers | Review all answers, especially for minor arithmetic mistakes |
Practice Tests for Exam Success
One of the most effective ways to prepare for any major test is by taking practice exams. These tests not only help you assess your knowledge but also familiarize you with the format and timing of the real exam. By simulating exam conditions, you can reduce anxiety and build confidence, making the actual test day less stressful.
Simulating test conditions is crucial to ensure that you are ready to manage your time and work through questions efficiently. When practicing, set a timer to replicate the time constraints of the real exam. This will help you become accustomed to pacing yourself and allow you to identify areas where you need more practice.
Reviewing your practice test results is just as important as taking the test itself. After completing each practice test, thoroughly review your mistakes and try to understand why you got them wrong. Focus on the areas where you struggle, and use this feedback to guide your future study sessions.
Top Resources for Exam Preparation
Accessing high-quality resources is essential for thorough exam preparation. With the right tools and materials, you can reinforce your understanding of key concepts and ensure that you’re ready for the challenges of the test. Below are some of the best resources that can help you prepare effectively.
Online platforms offer a wide range of practice problems, interactive lessons, and instructional videos. These resources are designed to guide you through complex topics step by step, allowing you to grasp difficult concepts at your own pace. Many websites also provide personalized learning plans based on your strengths and weaknesses.
Textbooks and study guides remain invaluable tools, providing structured reviews and exercises that mirror what you will encounter on the test. They often include example questions, as well as detailed solutions to help you understand the reasoning behind each answer.
How to Improve Problem-Solving Skills
Improving problem-solving skills is a critical part of performing well in any test. The ability to approach problems logically and methodically not only boosts confidence but also enhances overall test performance. With consistent practice and the right strategies, anyone can become more efficient at solving complex problems under time pressure.
Break Down the Problem
The first step in solving any problem is to break it down into smaller, more manageable parts. Start by identifying what is being asked and what information is given. This helps you focus on the most important elements and avoid getting overwhelmed. From there, think about which formulas or concepts can help you solve each part step by step.
- Identify known and unknown variables
- Look for relationships between the numbers and operations
- Organize the information before jumping into calculations
Practice Mental and Written Strategies
Being able to solve problems both mentally and in writing is essential. Start by practicing basic mental math to improve your speed and accuracy. When tackling more complex problems, write down your steps clearly. This not only helps you stay organized but also makes it easier to spot mistakes if they occur.
- Practice simple calculations to improve speed
- Write out every step to avoid skipping important details
- Use estimation to check the reasonableness of your answer
Time Management Tips for Exam Day
Effective time management on exam day is essential for maximizing your performance. Knowing how to allocate your time wisely ensures that you can complete all questions and review your work before submitting your exam. By using a few key strategies, you can stay focused and organized throughout the test.
Pre-Exam Preparation

Before the exam begins, make sure you have a clear plan for how you will approach each section. Set specific goals for each part of the test, and remember that time management is not just about speed–it’s also about strategy. Focus on your strengths first, and leave more challenging problems for later when you may be more warmed up.
- Review the exam structure to understand the timing of each section
- Prioritize questions based on difficulty and point value
- Bring all necessary materials (pens, pencils, ID, etc.) to avoid last-minute delays
During the Exam
During the exam, it’s important to keep track of time without feeling rushed. Use a clock or timer to monitor your progress, and try to maintain a steady pace throughout the test. If you get stuck on a question, don’t spend too much time on it. Move on and return to it later if you have time left over.
- Set a time limit for each question or section
- Skip tough questions and come back to them later
- Stay calm and focused, avoiding distractions
By managing your time effectively, you can approach each question with a clear mind and maximize your chances for success.
Important Formulas to Remember
Memorizing key formulas is essential for tackling problems efficiently in any math exam. Knowing the right equations at your fingertips allows you to solve problems faster and more accurately. Below are some of the most important formulas you should commit to memory for exam success.
Basic Arithmetic and Operations
These fundamental formulas are the building blocks for more advanced concepts and will help you in a wide range of problems.
- Distributive Property: a(b + c) = ab + ac
- Order of Operations: Parentheses, Exponents, Multiplication/Division (from left to right), Addition/Subtraction (from left to right)
- Percentage Formula: Part = (Percent × Whole) / 100
Linear Equations and Functions
Understanding the relationships between variables is crucial for solving equations and graphing functions.
- Slope-Intercept Form: y = mx + b (where m is the slope and b is the y-intercept)
- Point-Slope Form: y – y₁ = m(x – x₁) (where m is the slope and (x₁, y₁) is a point on the line)
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a (used to solve quadratic equations of the form ax² + bx + c = 0)
Factoring and Exponents
Mastering these formulas will help you simplify and solve complex expressions with ease.
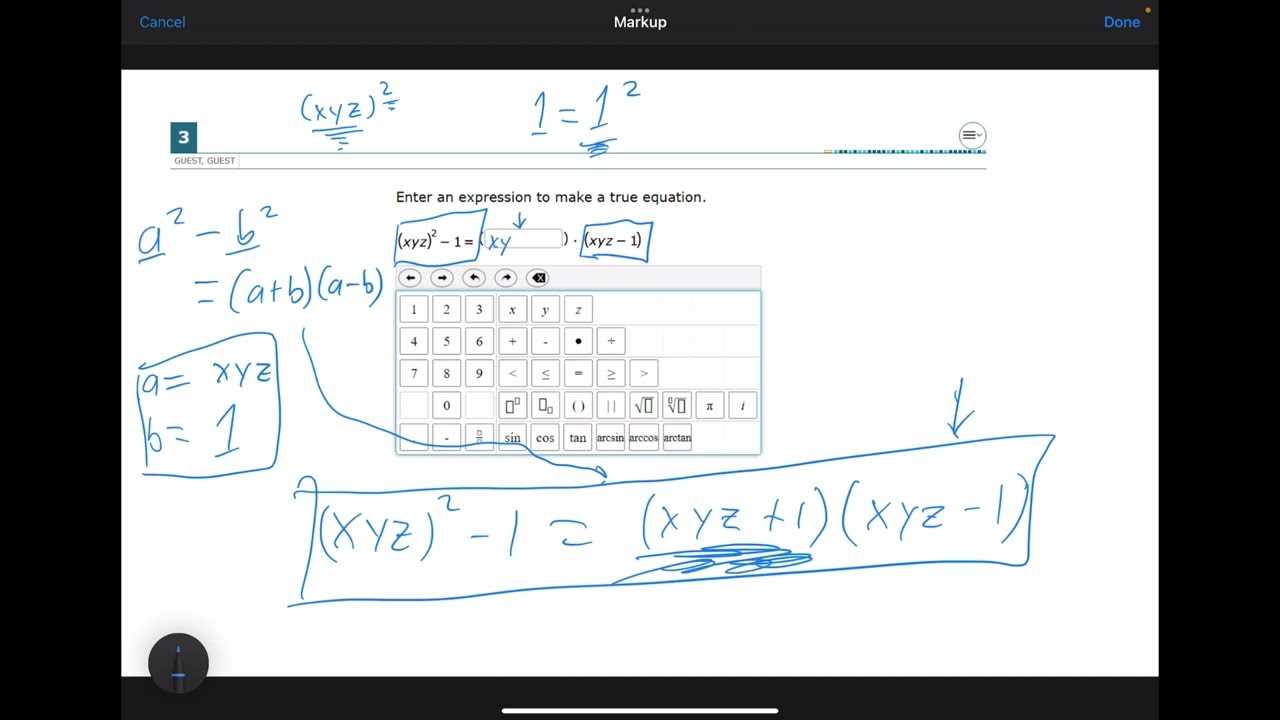
- Difference of Squares: a² – b² = (a + b)(a – b)
- Exponent Rules:
- a^m × a^n = a^(m+n)
- (a^m)^n = a^(m×n)
- a^0 = 1 (for any non-zero a)
By remembering and practicing these formulas, you’ll be well-equipped to handle a variety of mathematical challenges on your exam.
How to Stay Calm During the Exam
Maintaining composure during an exam is crucial for performing at your best. Feeling anxious or overwhelmed can hinder your ability to think clearly and focus on the questions at hand. By employing a few simple strategies, you can stay calm, organized, and confident throughout the test.
Practice Deep Breathing
One of the most effective ways to reduce anxiety is through deep breathing exercises. By focusing on your breath, you can quickly calm your mind and body. This technique helps lower stress levels and increases your ability to concentrate.
- Inhale slowly for 4 seconds, hold your breath for 4 seconds, then exhale slowly for 4 seconds.
- Repeat this cycle a few times to help calm your nerves.
Stay Positive and Focused

Keep a positive mindset during the exam. Remind yourself that you’ve prepared well and that you are capable of tackling each problem. Avoid negative thoughts and focus on one question at a time.
- Don’t dwell on questions you find difficult–move on and come back to them later if necessary.
- Visualize success and remind yourself that each challenge is just a step toward completing the exam.
By adopting these techniques, you’ll be better equipped to manage stress and approach the exam with a clear and calm mindset.
What to Do After Completing the Exam
After finishing your exam, it’s important to approach the next steps calmly and thoughtfully. This period can feel overwhelming, but staying focused will help you transition smoothly. Here’s what you can do to ensure you make the most of the time after completing the test.
Review Your Responses

If time permits, review your answers before submitting the exam. Often, a second look can help you catch small errors or incomplete responses. Make sure to check for:
- Any skipped questions
- Clear and legible handwriting
- Correct units or symbols in your answers
- Consistency in your calculations or reasoning
Stay Calm and Relax
Once you’ve reviewed your work, try to relax and avoid stressing over what might have been missed. It’s natural to wonder if you answered everything correctly, but worrying won’t change the outcome. Instead, focus on relaxing your mind and body:
- Take deep breaths
- Stretch your body to release tension
- Visualize your success and move forward with confidence
Prepare for the Next Steps
Once you’ve submitted your exam, it’s time to shift your attention to the future. Whether it’s awaiting results or preparing for future assignments, having a plan will help you stay productive:
- Review upcoming projects or tests
- Plan for your next study session
- Set new learning goals
By following these steps, you can transition from exam mode into your next tasks with a clear mind and a positive outlook.
Real-World Applications of Algebra 1 Concepts
The concepts learned in foundational mathematics have wide-ranging applications in everyday life and various professions. These skills not only help in academic settings but also provide essential tools for solving practical problems in the real world. By understanding how abstract principles work, you can apply them to situations that require logical thinking and problem-solving.
Managing Finances
Mathematical principles, such as solving equations, are frequently used in managing personal finances. Whether it’s calculating monthly expenses, setting up a budget, or understanding interest rates, the ability to manipulate numbers and solve for unknowns is crucial:
- Creating a budget using income and expenditure variables
- Understanding how loans or savings grow over time with compound interest
- Calculating discounts, tax, and tip amounts in shopping scenarios
Engineering and Architecture
In professions like engineering and architecture, mathematical concepts are foundational to designing structures, analyzing forces, and making calculations to ensure safety and efficiency. From the design of bridges to the layout of buildings, professionals rely on these skills:
- Calculating load distribution and structural integrity
- Designing efficient floor plans and creating scale models
- Estimating construction costs based on various variables
Computer Science and Technology
In the world of technology, algorithms and programming rely heavily on mathematical principles. Software development, data analysis, and machine learning all utilize mathematical reasoning to build effective systems:
- Writing algorithms that solve complex problems efficiently
- Optimizing code for better performance
- Building systems that handle large sets of data through computation
By mastering the fundamentals, students not only prepare for academic assessments but also gain skills that are applicable in many career fields and everyday situations. The use of mathematical thinking extends far beyond the classroom and plays a key role in navigating the challenges of modern life.
How Algebra 1 Affects Future Courses
The foundational concepts introduced in early mathematical studies play a significant role in shaping the trajectory of higher education. Mastery of these key principles is crucial not just for succeeding in subsequent courses but also for understanding more complex topics in various disciplines. The knowledge gained serves as a springboard for more advanced subjects, influencing both academic performance and future career paths.
Building a Strong Foundation for Advanced Math
As students progress through their education, understanding core mathematical concepts becomes increasingly important. The skills developed in early courses form the base upon which more challenging subjects are built. Topics like geometry, trigonometry, and calculus require a solid grasp of variables, equations, and functions, all of which are introduced at the beginning of one’s studies:
- Solving equations and inequalities in future math classes
- Applying functions and graphing in higher-level coursework
- Using logical reasoning and pattern recognition in problem-solving
Interdisciplinary Applications and Problem-Solving Skills
The knowledge acquired in introductory mathematics also extends beyond traditional math courses. It enhances students’ abilities in subjects like physics, economics, and computer science, where problem-solving and quantitative reasoning are essential. Students can apply these concepts in various fields:
- Understanding scientific principles through mathematical formulas
- Analyzing data and trends in economics and finance
- Designing algorithms and developing computer systems in technology courses
Ultimately, success in early mathematical courses paves the way for a deeper understanding of more advanced topics, benefiting students both in their academic journey and in their future careers. By mastering these foundational skills, students not only prepare for higher-level mathematics but also develop problem-solving abilities that are crucial across a wide range of fields.
Additional Support for Algebra 1 Students
Many students face challenges when learning core mathematical concepts, and it’s important to have a variety of resources available to provide assistance. Whether it’s extra practice, personalized tutoring, or digital tools, there are numerous ways to enhance understanding and build confidence. Access to supplementary help can make a significant difference in mastering the material and succeeding in math courses.
Types of Support Available
There are several types of additional support options that can aid students in strengthening their mathematical skills. These resources cater to different learning styles and can be used to address specific areas of difficulty:
| Support Type | Description |
|---|---|
| Tutoring | One-on-one assistance from a tutor can provide personalized instruction and help students work through complex problems at their own pace. |
| Online Resources | Websites and apps offer interactive lessons, exercises, and videos to reinforce concepts and allow students to practice on their own time. |
| Study Groups | Collaborating with peers in a group setting allows students to exchange ideas, clarify doubts, and reinforce learning through discussions and shared resources. |
| Classroom Resources | Teachers often provide additional worksheets, practice problems, and review materials to help students prepare for assessments and build their problem-solving abilities. |
Utilizing These Resources Effectively
It’s important for students to take a proactive approach when seeking additional help. Here are some tips to make the most of the available support:
- Set specific goals for each study session, focusing on particular concepts that need improvement.
- Ask questions and actively engage with tutors, teachers, or peers to clarify misunderstandings.
- Practice regularly to reinforce learning and gain confidence in solving various types of problems.
- Use online tools for extra practice, as they often provide instant feedback to help identify areas of weakness.
By utilizing the resources available, students can overcome challenges, improve their skills, and achieve greater success in their courses. The key is to seek support when needed and stay committed to consistent practice and learning.