
When starting out with foundational math topics, it’s crucial to grasp the basic principles that serve as building blocks for more advanced studies. Understanding the key concepts in this early stage sets the stage for success in solving equations, simplifying expressions, and interpreting problems correctly. Having a strong command of these fundamentals is essential for tackling more complex problems later on.
As you prepare for assessments in this area, focusing on developing problem-solving strategies is just as important as memorizing formulas. Learning to break down problems, apply the correct methods, and check your work will not only help you perform well on evaluations but also improve your overall math skills. With practice, you will gain confidence and ease in navigating mathematical challenges.
Effective preparation involves more than just reviewing material; it’s about understanding the logic behind each process and recognizing how different concepts are interconnected. Regular practice with sample questions and reviewing common mistakes will help you achieve the clarity needed to excel.
Understanding the Basics of Mathematical Foundations
At the heart of early math studies lies a set of core principles that form the foundation for all subsequent problem-solving and reasoning. Mastering these essentials is crucial for progressing through more complex material with confidence. In this section, we will focus on the fundamental concepts that provide the groundwork for developing strong mathematical skills.
By exploring the key elements of basic equations, operations, and relationships between variables, you’ll begin to understand the structure behind mathematical problems. This understanding is not only critical for solving specific exercises but also for recognizing patterns and applying the knowledge to more advanced topics.
| Concept | Description |
|---|---|
| Variables | Symbols representing unknown values or quantities in equations. |
| Expressions | Combinations of numbers, variables, and operations without an equal sign. |
| Equations | Mathematical statements with an equal sign showing equality between two expressions. |
| Operations | Basic actions such as addition, subtraction, multiplication, and division applied to numbers and variables. |
These key topics serve as the building blocks for progressing in mathematical thinking. Once you have a solid grasp of them, solving problems will become more intuitive and straightforward.
How to Prepare for the First Assessment
To succeed in the initial evaluation, it’s important to approach the preparation process strategically. Understanding the material thoroughly, practicing problem-solving techniques, and reviewing key concepts will ensure you feel confident and well-prepared when it’s time to apply your knowledge. This section provides a clear roadmap for effective preparation.
Review Key Concepts and Methods
Start by revisiting the core principles and techniques introduced in the beginning. Make sure you understand how to manipulate variables, solve simple equations, and apply basic operations to different problems. Here are some effective steps to follow:
- Go over class notes and textbooks to refresh your memory on foundational concepts.
- Identify common patterns in problem types and learn how to approach each one.
- Understand how to break down more complex problems into smaller, manageable steps.
Practice with Sample Problems
The more problems you solve, the more comfortable you will become with applying the methods learned. It’s essential to practice not only the exercises covered in class but also additional problems that test your understanding of various topics. Consider the following approaches:
- Work through problems from previous assignments to reinforce your knowledge.
- Find extra practice worksheets or online resources that offer a wide range of problems.
- Set aside time to complete timed exercises to simulate the test environment.
Consistent practice with these strategies will help you develop the necessary skills and confidence to succeed in the assessment.
Key Concepts to Master in the First Section
To build a solid foundation for future learning, it’s crucial to master the core ideas introduced early in the curriculum. These fundamental concepts are not only essential for solving problems but also form the basis for more advanced techniques. In this section, we will highlight the key areas you need to focus on for a strong understanding of the material.
Understanding Variables and Expressions
One of the first concepts to fully grasp is how variables work. Variables are symbols that represent unknown values and are often the starting point for solving equations. It’s important to understand how to read, write, and manipulate expressions involving these symbols. Being comfortable with this idea allows you to tackle a wide range of problems efficiently.
Operations and Simplification
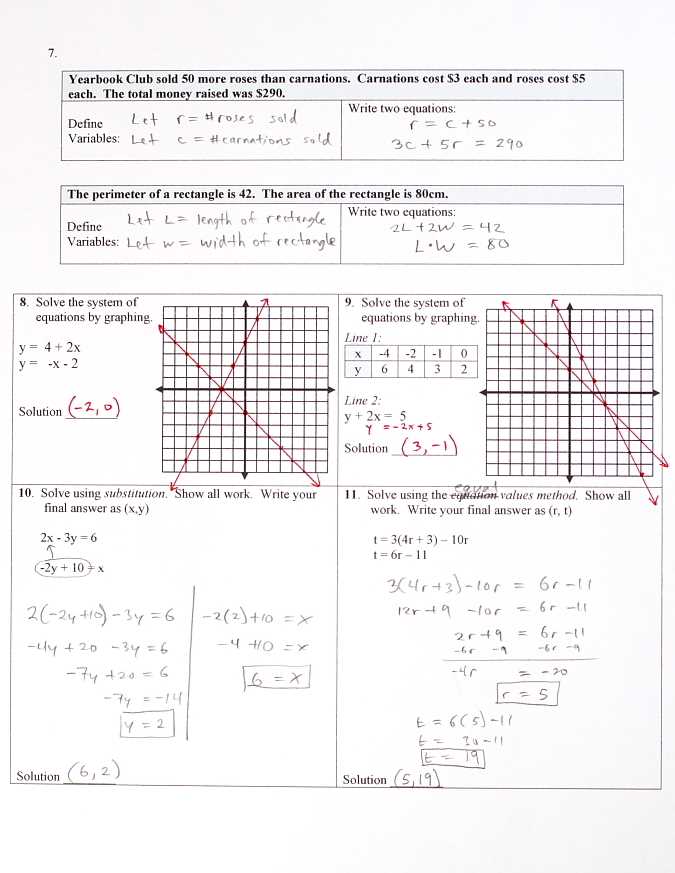
Equally important is understanding how different operations–addition, subtraction, multiplication, and division–interact with variables and numbers. Mastering how to apply these operations within expressions and simplifying them is essential for progressing to more complex tasks. A strong command of simplification techniques helps you recognize patterns and avoid common mistakes when solving equations.
By focusing on these key areas, you’ll develop the necessary skills to confidently approach more challenging problems in the future.
Step-by-Step Solutions for Practice Problems

To effectively master the skills needed for solving mathematical problems, it’s essential to break down each exercise into manageable steps. By approaching each problem systematically, you can better understand the process and apply the right techniques to reach the correct solution. This section will guide you through the problem-solving process using detailed steps.
Each problem should be approached with a clear strategy. Start by identifying the variables and the operations involved. Then, apply the appropriate methods to simplify and solve the equation. It’s important to check your work at each step to avoid errors and ensure the solution is accurate. Let’s explore this process with a sample problem:
Example Problem: Solve for x: 3x + 5 = 14
- Step 1: Subtract 5 from both sides to isolate the term with the variable.
3x = 14 – 5
3x = 9
- Step 2: Divide both sides by 3 to solve for x.
x = 9 ÷ 3
x = 3
By following these steps, you’ll be able to approach similar problems with greater confidence and accuracy.
Common Mistakes to Avoid in Mathematical Problem Solving
When working through mathematical exercises, it’s easy to make errors that can lead to incorrect solutions. Recognizing these common pitfalls early on can help you develop more accurate problem-solving habits. By being aware of typical mistakes, you can prevent them from becoming obstacles in your learning journey.
One frequent mistake is failing to follow the correct order of operations. Skipping steps or performing calculations out of sequence often results in incorrect results. Another common error is misinterpreting the problem, especially when variables or constants are involved. It’s important to carefully read each question and ensure you understand what is being asked before attempting to solve it.
Additionally, be mindful of sign errors. Whether it’s adding instead of subtracting or multiplying when division is required, small missteps in operations can lead to big mistakes. Regular practice and attention to detail are key to avoiding these errors and improving your overall accuracy.
Test-Taking Strategies for the First Assessment
Effective test-taking strategies are essential for maximizing performance during an evaluation. By preparing mentally and using a structured approach, you can tackle questions with confidence and accuracy. This section outlines key techniques that will help you approach the assessment with a clear plan, minimizing stress and optimizing results.
Start by quickly scanning through the entire set of problems. This will give you an overview of the content and help you prioritize questions. Tackle the ones that seem easiest first, as this will build confidence and give you more time for the more difficult problems. Be sure to manage your time effectively, allocating enough time for each section without rushing through any part.
Another important strategy is to double-check your answers, especially for calculations involving multiple steps. Mistakes can be easy to overlook in complex problems, so reviewing your work can help catch errors before submitting your results. Finally, stay calm and focused–panic can often lead to careless mistakes. By remaining composed, you can approach each question with clarity and solve it more efficiently.
Practice Questions for the First Section
Practicing with a variety of problems is one of the best ways to reinforce your understanding and prepare for any evaluation. By working through different types of exercises, you can familiarize yourself with the concepts and refine your problem-solving skills. In this section, you’ll find practice questions that cover the key topics introduced in the beginning, offering a chance to apply what you’ve learned.
Example Problems to Solve
These sample exercises are designed to test your ability to work with basic operations, expressions, and equations. Try solving each one and double-check your methods for accuracy.
- Solve for x: 4x – 7 = 13
- Simplify the expression: 3(2y + 4) – 5y
- Evaluate: 5a + 3 when a = 4
- Solve for y: 2y + 6 = 18
Practice Tips for Success
As you work through these questions, focus on understanding each step involved in reaching the solution. If you make a mistake, analyze where things went wrong and correct it. This practice will help solidify your grasp on the material and prepare you for more complex problems down the line.
Breaking Down Algebraic Expressions
Understanding how to break down and simplify algebraic expressions is a fundamental skill in mathematics. By identifying the components of an expression, such as variables, coefficients, and constants, you can effectively manipulate and simplify it. This section will guide you through the process of breaking down expressions step by step, making complex problems more manageable.
Start by recognizing the individual parts of an expression. Variables represent unknown quantities, while coefficients are the numbers that multiply those variables. Constants are simply fixed values added or subtracted from the expression. Once you’ve identified these components, you can apply the correct operations to simplify or solve the expression.
| Expression | Parts Breakdown | Simplified Form |
|---|---|---|
| 3x + 5 | Variable: x, Coefficient: 3, Constant: 5 | 3x + 5 |
| 2(4y – 3) | Coefficient: 2, Variable: y, Constant: -3 | 8y – 6 |
| 5a + 4a – 7 | Variables: a, Coefficients: 5, 4, Constant: -7 | 9a – 7 |
By following this approach, you can break down any algebraic expression, identify its components, and simplify it step by step for easier solving.
Tips for Solving Word Problems Efficiently
Word problems can often seem challenging, but with the right approach, they can be tackled more easily. The key to solving these types of problems is to break down the information provided and translate it into mathematical terms. This section offers practical tips to help you solve word problems quickly and accurately, ensuring you approach each problem with clarity.
- Read the problem carefully: Take your time to understand the context and what is being asked. Identify the important details and ignore unnecessary information.
- Identify the variables: Determine what you need to find and assign variables to represent unknown values. This will help you set up an equation or expression.
- Translate the words into math: Convert the given information into a mathematical equation. Look for keywords like “total,” “difference,” “product,” or “sum” to guide you in forming the equation.
- Organize the information: Write down the known values and the relationships between them. This helps in visualizing the problem and setting up the right approach.
- Double-check your work: Once you’ve solved the problem, review the question and your solution. Ensure the answer makes sense in the context of the problem.
By following these strategies, you can approach word problems with confidence, making the process of solving them much more efficient and less overwhelming.
Importance of Understanding Variables
Variables are essential components in mathematics as they represent unknown quantities that we need to solve for. A strong grasp of how to handle variables is crucial, as they appear in nearly every mathematical expression or equation. By understanding variables, you can translate real-world problems into solvable mathematical forms, which is an invaluable skill in problem-solving.
Mastering variables allows you to manipulate equations and expressions efficiently. Whether you’re adding, subtracting, multiplying, or dividing terms, knowing how to work with variables ensures that you can approach even the most complex problems systematically. This foundational skill lays the groundwork for more advanced topics in mathematics and other fields.
Key Properties of Variables

| Variable | Role | Example |
|---|---|---|
| x | Represents an unknown quantity to solve for | Solve for x in the equation: 2x + 3 = 7 |
| y | Used in expressions and equations for a second unknown | Solve for y in the equation: 3y – 5 = 10 |
| n | Typically used as a placeholder for counting or number sequences | Find the value of n in the expression: n + 4 = 10 |
Why Variables Matter
Without understanding how variables function, it would be impossible to approach and solve many types of problems. From basic equations to complex real-world applications, variables help represent and simplify relationships. Gaining confidence in handling variables enables you to move forward in your mathematical studies and solve problems with ease.
Using the Order of Operations Correctly
When solving mathematical expressions, it’s essential to follow a specific sequence of steps to ensure the correct result. The order in which operations are performed can significantly impact the outcome of a problem. Understanding and applying this sequence accurately is critical to solving problems effectively and avoiding common mistakes.
The order of operations dictates the sequence in which different operations–such as addition, subtraction, multiplication, division, and parentheses–should be carried out. If you don’t follow this rule, you risk getting an incorrect answer, even if the individual steps are done correctly.
Remember the Acronym PEMDAS
The acronym PEMDAS helps you recall the correct order of operations:
- P: Parentheses
- E: Exponents
- M: Multiplication
- D: Division
- A: Addition
- S: Subtraction
Operations inside parentheses should be completed first, followed by any exponents, then multiplication and division (from left to right), and finally, addition and subtraction (from left to right).
Example of Correct Application
Consider the expression: 3 + 5 × (2^2)
To solve this:
- First, handle the exponent: 2^2 = 4
- Next, evaluate the parentheses: 3 + 5 × 4
- Then, perform multiplication: 5 × 4 = 20
- Finally, perform the addition: 3 + 20 = 23
Following the order of operations gives the correct result: 23.
By applying the order of operations consistently, you can approach mathematical expressions with confidence, ensuring that you get accurate results every time.
Reviewing Graphing Techniques in Chapter 1
Understanding how to plot and interpret graphs is a fundamental skill that plays a key role in solving mathematical problems. The ability to represent relationships visually can simplify complex equations and make abstract concepts easier to understand. In this section, we will review the essential techniques for graphing that are introduced early on in mathematical studies.
Graphs provide a visual representation of equations, helping to identify patterns, trends, and solutions more intuitively. By plotting points on a coordinate plane, you can gain insights into how variables interact and how changes in one affect the other. Whether dealing with linear equations or more advanced functions, mastering graphing techniques is crucial for success in mathematics.
To graph successfully, it’s important to understand how to translate equations into coordinates, how to choose appropriate scales for the axes, and how to accurately plot points. This skill set is not only foundational for future topics but also essential for tackling word problems and real-world scenarios where data visualization is required.
How to Tackle Linear Equations
Solving equations that involve only variables to the first power can be a straightforward process once you understand the basic techniques. These types of problems typically involve finding the value of a variable that makes the equation true. By following a clear, step-by-step approach, you can simplify these problems and arrive at the correct solution with ease.
The key to solving linear equations lies in isolating the variable on one side of the equation. To achieve this, you must use inverse operations such as addition, subtraction, multiplication, and division. Each step brings you closer to finding the value of the unknown that satisfies the equation.
Step 1: Begin by simplifying both sides of the equation if necessary. Combine like terms and eliminate parentheses to make the equation clearer.
Step 2: Use inverse operations to move constants or coefficients away from the variable. For instance, if the variable is being multiplied by a number, divide both sides of the equation by that number.
Step 3: Continue applying inverse operations until the variable is isolated on one side. At this point, you can easily solve for its value.
Step 4: Finally, check your solution by substituting the value of the variable back into the original equation to ensure both sides are equal.
By practicing these steps, you will become more efficient at solving similar equations and gain confidence in tackling problems that require logical reasoning and numerical skills.
Test Review for Chapter 1 Success
Preparing for an upcoming evaluation is an essential step in achieving success. To feel confident and ready, it is important to review key concepts and practice essential skills. By revisiting core topics, identifying areas of weakness, and practicing with sample problems, you can ensure you are well-prepared and capable of solving problems effectively during the assessment.
Focus on the following strategies to maximize your review efforts:
- Identify Key Topics: Make a list of the main concepts covered, such as solving equations, graphing, or working with expressions.
- Review Notes and Textbooks: Go over your class notes, textbook examples, and any supplementary materials to refresh your memory on the methods used to solve problems.
- Practice with Exercises: Solving practice questions is one of the most effective ways to test your understanding. Work through examples similar to those you might encounter on the assessment.
- Seek Clarification: If you encounter any challenges, don’t hesitate to ask for help. Discussing difficult concepts with a teacher or classmate can provide valuable insights.
- Simulate the Environment: Practice solving problems within a set time frame to replicate the conditions of the evaluation. This will help you manage time effectively during the actual assessment.
By using these review techniques, you can boost your understanding, improve your problem-solving skills, and approach your evaluation with confidence. The more effort you put into preparing, the better your chances for success.
Understanding Functions and Their Properties
In mathematics, the concept of a relationship between variables is fundamental to solving a wide range of problems. Understanding how values are linked through specific rules helps us grasp essential principles that apply to many situations. By studying the characteristics of these relationships, such as domain, range, and behavior, one can gain a deeper insight into how to manipulate and solve related equations.
The Basics of Functions
A function is a special type of relationship where every input has exactly one output. The input is often referred to as the independent variable, while the output is the dependent variable. By studying the structure and form of a function, we can predict the output values based on specific inputs, which is key to solving many problems in mathematics.
Key Properties of Functions

When analyzing a function, several key properties come into play, which can help determine its behavior and assist in solving problems. Below are some of the most important aspects to understand:
| Property | Description |
|---|---|
| Domain | The set of all possible input values for which the function is defined. |
| Range | The set of all possible output values that the function can produce. |
| Increasing/Decreasing | Indicates whether the function is increasing or decreasing over a certain interval of inputs. |
| Continuity | Describes whether the function is continuous without jumps or breaks in its graph. |
These properties form the foundation of understanding how different functions behave, whether in simple equations or complex problems. Mastery of these concepts will help you better interpret the relationships between variables and effectively solve related tasks.
What to Expect in the Algebra 1 Test
Preparing for an assessment focused on the fundamentals of mathematical relationships can be a daunting task. Understanding what you will encounter on the exam is key to developing a focused study plan. The assessment will likely cover a range of topics, testing your ability to solve problems and demonstrate your understanding of key concepts. By familiarizing yourself with the format and types of questions, you can confidently approach the challenge.
Key Topics Covered
In this assessment, you can expect to encounter various concepts that are central to building a strong mathematical foundation. These topics will test your ability to work with equations, solve for unknowns, and apply logical reasoning to problems. Here are the main areas to focus on:
- Basic Operations: Adding, subtracting, multiplying, and dividing numbers, variables, and expressions.
- Linear Equations: Identifying and solving equations involving one or more variables.
- Graphing: Understanding how to plot points and interpret the graph of a relationship.
- Working with Variables: Identifying and manipulating variables in equations and expressions.
- Word Problems: Applying mathematical concepts to solve real-world scenarios and interpret problem situations.
What the Questions Will Look Like
The questions on the exam will vary in format, testing both your computational and conceptual knowledge. You might encounter the following types of questions:
- Multiple Choice: Choose the correct option based on your understanding of the material.
- Fill-in-the-Blank: Provide the correct value or expression in response to a question.
- Problem Solving: Solve for unknown variables and demonstrate your reasoning step by step.
- Graph Interpretation: Analyze a graph and answer questions related to its properties or data points.
To perform well, it’s important to review both the technical aspects of calculations and the application of concepts in various contexts. Keep practicing problems and familiarize yourself with the types of questions you are likely to face on the assessment. With focused preparation, you can approach the exam with confidence and clarity.
Building Confidence for Your Exam
Approaching an assessment with confidence is crucial for performing well. It’s natural to feel some anxiety, but there are practical steps you can take to ease your nerves and ensure you’re well-prepared. Understanding the material, practicing regularly, and adopting a positive mindset will all help you build the self-assurance needed to tackle the challenges ahead.
Effective Study Strategies
To boost your confidence, it’s important to have a structured approach to studying. Consistent practice and focused review can make a significant difference. Here are some tips to enhance your preparation:
- Break Down the Material: Focus on smaller sections of the content to avoid feeling overwhelmed. Master one concept before moving to the next.
- Practice Regularly: Solve problems daily to reinforce your understanding and improve your problem-solving skills.
- Use Different Resources: Review your notes, use online tutorials, or consult textbooks for different explanations of challenging concepts.
- Simulate Test Conditions: Practice under timed conditions to become comfortable with the exam format and improve time management.
- Review Mistakes: Take time to understand any errors you make during practice. This will help you avoid making the same mistakes on the actual exam.
Maintaining a Positive Mindset
A positive mindset can help you overcome stress and stay focused during the exam. Here are some techniques to maintain your confidence:
- Stay Positive: Focus on what you know, rather than stressing over the things you’re unsure of.
- Visualize Success: Picture yourself succeeding in the exam, which can help reduce anxiety and improve performance.
- Get Adequate Rest: A well-rested mind functions better, so make sure to get enough sleep before the exam day.
- Practice Mindfulness: Engage in relaxation techniques such as deep breathing or meditation to stay calm and clear-headed.
By following these strategies, you can approach your exam with the confidence and clarity needed to perform at your best. Trust in your preparation and take one step at a time to achieve success.