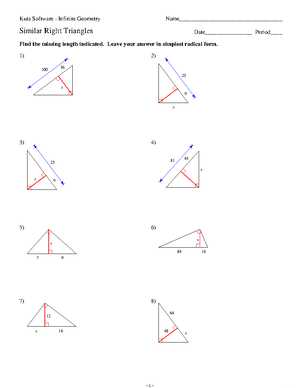
Achieving proficiency in mathematics requires not only understanding fundamental principles but also the ability to apply them effectively during evaluations. As students approach their final assessments, reinforcing knowledge through consistent practice becomes crucial. Tackling sample questions helps identify strengths and areas for improvement, ensuring better performance when faced with real exam challenges.
By reviewing common problem types and familiarizing oneself with different approaches to solutions, students can significantly boost their confidence and problem-solving speed. Success lies in mastering key strategies and eliminating confusion that may arise under timed conditions. Focused preparation allows individuals to develop a deeper understanding of essential mathematical skills and concepts that are integral to achieving top scores.
Utilizing available resources, such as previous questions and expert insights, can further enhance study efficiency. By practicing in a structured way, students can build the confidence needed to tackle even the most complex tasks with ease and precision.
Understanding the Structure of the Final Assessment
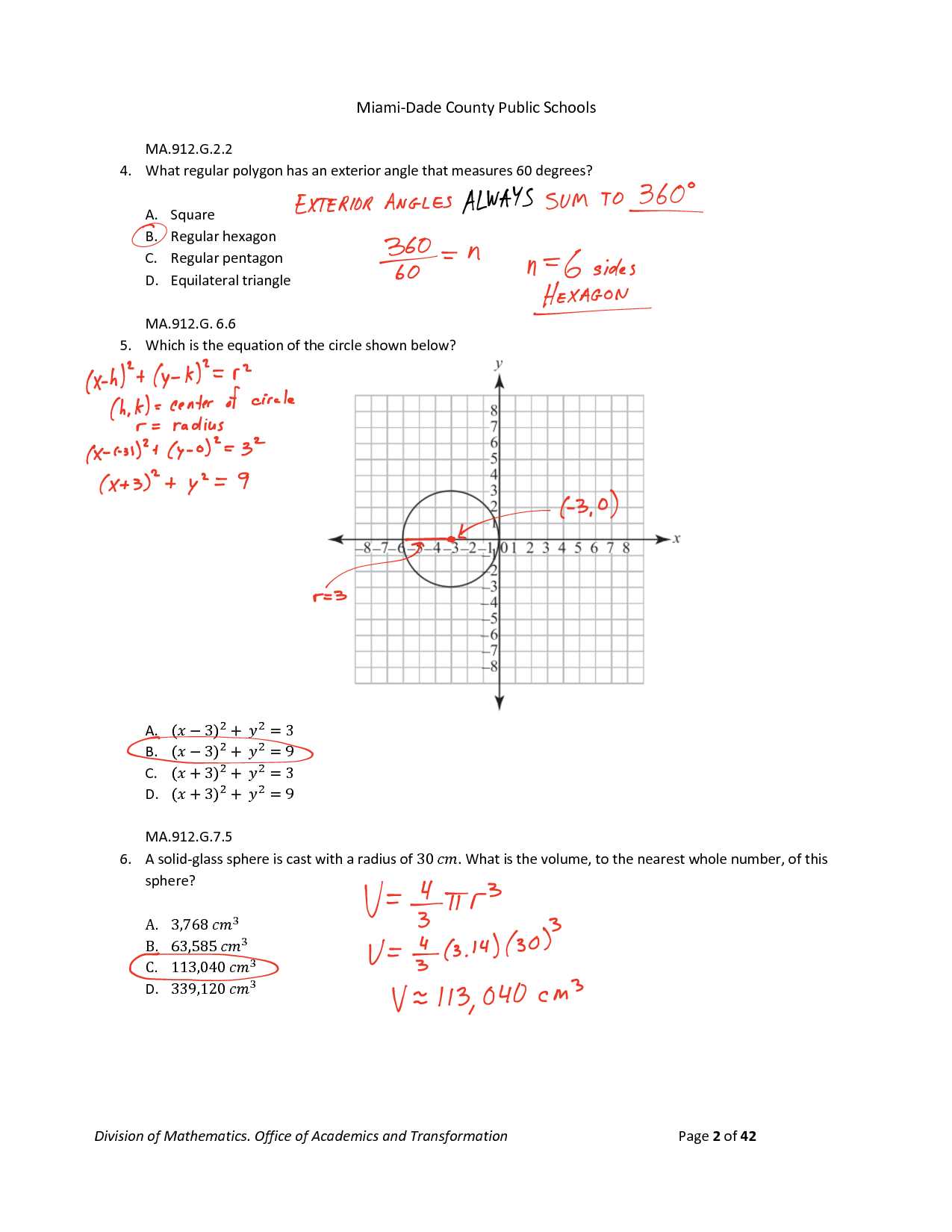
To excel in any evaluation, it is essential to understand its layout and requirements. Familiarizing yourself with the structure of the assessment will help reduce anxiety and allow for more effective preparation. Knowing what types of questions to expect and how they are distributed can make all the difference in managing time and strategy.
Components of the Assessment
The assessment typically consists of various sections that test a range of skills, from basic principles to more complex problem-solving tasks. Each part of the evaluation is designed to assess different levels of understanding and application of key concepts.
- Multiple Choice Questions: These questions assess the ability to quickly identify correct answers from a set of options, focusing on theoretical knowledge and formula application.
- Open-Ended Problems: These problems require the student to explain their thought process and show detailed steps to arrive at the correct solution.
- Word Problems: These questions test critical thinking by presenting real-life scenarios where mathematical concepts must be applied.
Strategies for Success
To approach the assessment with confidence, it is important to use targeted strategies. Understanding how questions are designed can help prioritize which topics to focus on during preparation.
- Review Key Concepts: Focus on foundational ideas that are frequently tested, such as basic properties, equations, and problem-solving techniques.
- Time Management: Allocate a specific amount of time to each section based on its complexity and point value.
- Practice with Sample Questions: Regularly solve practice problems to build familiarity with question types and improve speed.
Key Concepts for Exam Success
To perform well in any final assessment, mastering certain core principles is essential. These foundational ideas not only form the basis of problem-solving but also help in applying strategies across a variety of question types. Understanding these concepts thoroughly ensures that you are well-equipped to approach the exam with confidence.
Core Theoretical Principles
Many problems will require you to apply fundamental concepts that are often tested in different ways. Being able to recall and utilize these ideas efficiently is crucial for solving both simple and complex questions.
- Shapes and Figures: Understand the properties and classifications of various geometric shapes like triangles, circles, and quadrilaterals. Know how to calculate their areas, perimeters, and other key attributes.
- Angles and Lines: Master the relationships between angles, parallel lines, and transversals. Recognize complementary, supplementary, and vertical angles in different scenarios.
- Congruence and Similarity: Be familiar with the conditions under which figures are congruent or similar, and how to use proportionality for solving problems.
Applied Problem-Solving Techniques

In addition to theoretical knowledge, it is important to develop a practical understanding of how to apply these concepts to real-world problems.
- Use of Formulas: Be prepared to apply a range of formulas, such as those for calculating the area, volume, and surface area of different shapes.
- Logical Reasoning: Develop the ability to approach problems step by step, making logical deductions and justifications for each solution.
- Word Problem Strategies: Learn to translate word problems into mathematical expressions, identifying the key information needed to solve them.
Effective Study Strategies for Success
To succeed in any mathematical evaluation, developing efficient study habits is key. Effective preparation requires more than just reviewing material–it’s about honing skills and understanding how to approach different problem types. Focusing on both theory and application is essential for mastering key concepts and performing well under exam conditions.
One of the best ways to prepare is by organizing your study sessions and using a variety of techniques that target different aspects of learning. Combining active recall with regular practice and analysis of mistakes can accelerate your understanding and boost your confidence.
Study Schedule and Prioritization
A structured approach to studying helps ensure that all areas are covered in a balanced way. Prioritize difficult topics while maintaining a steady review of easier material to reinforce your knowledge.
| Study Topic | Time Allocation | Focus Area |
|---|---|---|
| Basic Principles | 1 hour | Review fundamental concepts and formulas |
| Problem Solving | 1.5 hours | Apply concepts to solve sample problems |
| Advanced Applications | 1 hour | Work on complex problems and word questions |
| Review Mistakes | 30 minutes | Analyze errors and learn from them |
Active Learning Techniques
Incorporating active learning strategies is an effective way to reinforce concepts and improve retention. This includes explaining topics in your own words, creating summary notes, and solving problems without looking at the solutions first.
- Concept Mapping: Visualize how different ideas connect to one another.
- Practice with Timed Sessions: Simulate real exam conditions to improve time management and reduce test anxiety.
- Group Study: Discuss challenging topics with peers to gain new perspectives and insights.
How to Approach Mathematical Exam Questions
When faced with exam questions, the key to success lies in developing a systematic approach that helps you break down each problem efficiently. Whether it’s identifying the right formula or drawing diagrams to visualize the problem, having a clear strategy can greatly improve both speed and accuracy.
Understanding how to tackle different types of questions is essential. Some require straightforward calculations, while others demand more complex reasoning. Regardless of the complexity, staying organized and focused will help you maximize your performance.
Step-by-Step Approach
Breaking down the problem into manageable steps is crucial. Here’s how you can approach questions with ease:
- Read the Question Carefully: Take the time to understand what is being asked before diving into calculations. Identify key information like numbers, shapes, and relationships.
- Identify Relevant Concepts: Determine which principles, formulas, or properties apply to the problem.
- Draw Diagrams: Visualizing the problem often makes it easier to identify relationships and solve for unknowns.
- Plan Your Steps: Before solving, outline the steps you need to take, from applying formulas to simplifying expressions.
- Check Your Work: After solving, review your calculations and reasoning to ensure there are no mistakes.
Effective Problem-Solving Techniques
Different types of questions require different strategies. Here are some common techniques for solving them:
- For Word Problems: Translate the situation into mathematical expressions. Identify keywords that indicate operations like “sum,” “difference,” “product,” or “quotient.”
- For Proofs: Focus on logical reasoning, starting with known facts and moving step-by-step to prove the statement.
- For Multiple-Choice Questions: Eliminate obviously wrong answers first, and if necessary, test the remaining options.
Common Mistakes in Mathematical Assessments
When preparing for any assessment, it’s crucial to recognize the common errors that can hinder performance. Even the most knowledgeable students can fall victim to simple mistakes that affect their overall score. Understanding these pitfalls allows for better preparation and a more efficient approach during the evaluation.
By learning from frequent errors, students can develop strategies to avoid them and improve their ability to apply concepts correctly under pressure. Some of these mistakes are subtle, while others stem from a lack of attention to detail or rushing through problems.
Frequent Mistakes to Avoid
Below are some of the most common mistakes and strategies for avoiding them:
| Common Mistake | How to Avoid It | Impact on Results |
|---|---|---|
| Misunderstanding the Question | Carefully read each question and underline key information before proceeding. | Leads to irrelevant solutions or missed steps. |
| Forgetting to Label Diagrams | Always label all angles, sides, and important points in diagrams. | Prevents clear analysis and makes solving difficult. |
| Using Incorrect Formulas | Review and memorize formulas ahead of time, and double-check which one applies to each question. | Results in incorrect answers, especially for complex calculations. |
| Skipping Units or Dimensions | Ensure all units are included and converted as necessary, especially when dealing with area, perimeter, or volume. | Can lead to wrong answers due to mismatched units. |
| Overcomplicating Problems | Simplify problems by identifying the most straightforward solution path, and avoid unnecessary steps. | Wastes time and increases the chance of errors. |
Step-by-Step Solutions for Mathematical Problems

When solving complex problems, breaking them down into smaller, manageable steps is essential for clarity and accuracy. A systematic approach ensures that you don’t miss any crucial details and can confidently work through the solution process. This method not only helps in arriving at the correct answer but also reinforces your understanding of the underlying principles.
By following a structured procedure, you can tackle various types of questions efficiently. Below is an example of how to approach and solve a typical problem using a step-by-step method. This approach helps identify key information, apply the right formulas, and check your work as you go along.
Example Problem: Finding the Area of a Circle
In this example, we will solve the problem of finding the area of a circle given its radius. The solution will be broken down into simple steps to follow:
| Step | Action | Explanation |
|---|---|---|
| 1 | Write down the formula for area. | The formula to find the area of a circle is: A = πr², where A is the area and r is the radius. |
| 2 | Identify the given information. | The problem provides the radius of the circle, which is 5 units. |
| 3 | Substitute the values into the formula. | Using the formula A = πr², substitute r = 5: A = π(5)². |
| 4 | Calculate the result. | Now calculate the square of 5: A = π(25). Using π ≈ 3.14, we get A ≈ 3.14 * 25 = 78.5 units². |
| 5 | Review the result. | Ensure that the units are correct (square units in this case) and the calculation matches the expected outcome. |
By following these steps, you can confidently solve similar problems and build a strong foundation for tackling other types of questions.
Using Practice Sessions to Improve Scores
Engaging in regular review sessions is one of the most effective ways to boost performance. By simulating the actual evaluation environment, you can familiarize yourself with the format and types of questions, enhancing your ability to respond confidently and efficiently. These review exercises also help identify areas of weakness, allowing for targeted improvement.
Repetition is key to mastering the material. The more you expose yourself to different problem types, the more comfortable you become with solving them under time constraints. Additionally, these sessions give you the opportunity to fine-tune your strategies for approaching questions, ensuring that you can apply your knowledge with precision when it matters most.
Through consistent practice, you can not only reinforce existing knowledge but also discover new methods for tackling challenges. This approach helps build both skill and confidence, which are essential for achieving a high score in any evaluation.
Analyzing Mathematical Questions and Solutions
To truly excel in any assessment, it’s important not only to answer questions correctly but also to understand the reasoning behind each solution. Analyzing both the questions and solutions helps to reinforce key concepts and identify patterns, ensuring that you can apply your knowledge to a variety of problems.
Breaking down the structure of each question allows you to uncover the specific skills needed for a correct response. By evaluating how each solution is derived, you improve your problem-solving abilities and gain insight into areas where you may need further practice or clarification.
Understanding Question Structure
Each problem is designed to test certain skills, such as logic, calculation, or reasoning. By paying attention to the wording and structure, you can identify the most efficient method for approaching the solution. Here’s how to approach any given question:
- Identify Key Information: Focus on the numbers, variables, and relationships mentioned in the question.
- Determine the Required Outcome: Understand what the question is asking for–whether it’s a value, an explanation, or a proof.
- Choose the Correct Method: Recognize which principle, formula, or strategy applies best to solve the problem.
Evaluating Solutions
Once you’ve solved a problem, it’s important to review your steps and understand how the solution was reached. This analysis helps you spot any mistakes and strengthens your understanding of the concepts involved:
- Check Calculations: Ensure that all steps are correct and no arithmetic errors were made.
- Verify Logical Flow: Make sure the solution follows a clear, logical progression from start to finish.
- Reflect on Alternate Approaches: Consider if there’s another way to solve the problem that might be quicker or more efficient.
Time Management Tips for Assessments
Effective time management is crucial when preparing for any assessment. It’s not just about knowing the material; it’s about managing your time wisely during the actual evaluation. By strategically allocating time to each section or question, you can ensure that you have the opportunity to address all problems without feeling rushed or overwhelmed.
Planning ahead and practicing time management can reduce stress and increase your efficiency. Developing these skills beforehand will help you stay calm and focused during the actual assessment, allowing you to maximize your performance.
Strategies for Effective Time Allocation
Below are some tips to help you manage your time effectively during an assessment:
- Prioritize Easier Questions: Start with questions that you find easier or are more familiar with. This ensures you accumulate quick points and build confidence.
- Allocate Time to Each Section: Before you start, take a few moments to decide how much time to spend on each section of the assessment. Stick to this plan as closely as possible.
- Don’t Get Stuck on One Question: If you find yourself spending too much time on one question, move on to the next one. You can always come back to it later if time allows.
- Keep Track of Time: Regularly check the time during the assessment. This will help you pace yourself and avoid rushing towards the end.
Managing Time During Practice Sessions
It’s also essential to practice time management while preparing. By timing yourself during practice exercises, you can become accustomed to working within time limits. Here are some strategies for practicing time management:
- Simulate Real Conditions: Set a timer when practicing so that you can get used to working under time pressure.
- Review and Adjust: After each practice session, evaluate how well you managed your time. If you didn’t finish on time, identify areas where you can improve.
- Focus on Speed and Accuracy: Aim to solve problems quickly without sacrificing accuracy. Practice solving problems efficiently without rushing through them.
Understanding Mathematical Formulas and Theorems
Mastering the core formulas and theorems is essential for solving problems effectively in any mathematical evaluation. These rules and principles form the foundation for solving complex problems, providing structured methods to approach a variety of challenges. Understanding their applications, derivations, and relationships will significantly improve problem-solving skills and efficiency.
Rather than memorizing formulas in isolation, it’s important to grasp how they work and why they are used. By understanding the logic behind these rules, you can apply them more intuitively and adjust them to fit different scenarios. This deeper comprehension will make mathematical challenges more approachable and manageable.
Key Formulas You Should Know
Here are some of the most important formulas that frequently appear in mathematical challenges:
- Pythagorean Theorem: a² + b² = c² – Used to find the length of a side in a right-angled triangle.
- Area of a Rectangle: Area = length × width – Calculate the area by multiplying the length and width.
- Circumference of a Circle: C = 2πr – The distance around the circle, calculated by multiplying 2, pi, and the radius.
- Volume of a Sphere: V = (4/3)πr³ – The amount of space inside a sphere, based on the radius.
- Area of a Triangle: A = ½ × base × height – To find the area of a triangle, multiply the base by the height and divide by 2.
Common Theorems and Their Applications
Theorems are crucial for understanding relationships between different figures. Here are some essential theorems:
- Angle Sum Theorem: The sum of the angles in a triangle is always 180°.
- Vertical Angle Theorem: When two lines intersect, the opposite angles (vertical angles) are congruent.
- Parallel Postulate: If two lines are parallel, then the corresponding angles formed by a transversal are congruent.
- Congruence Theorems (SSS, SAS, ASA): Methods for proving two triangles are congruent based on their sides and angles.
These formulas and theorems are not only essential for solving individual problems but also form the core principles that will help you approach complex mathematical questions with confidence and clarity.
Tips for Memorizing Mathematical Definitions
Mastering definitions is an important part of understanding and applying mathematical concepts. These terms often form the foundation for more complex ideas, and knowing them well can help you solve problems more efficiently. However, memorizing all the definitions can be overwhelming, so it’s essential to use strategies that make the process easier and more effective.
One of the best approaches is to break down definitions into smaller, manageable chunks. Rather than trying to memorize everything at once, focus on understanding the key elements and relationships behind each term. Using repetition, associations, and real-world examples can also help reinforce your memory and deepen your understanding.
Effective Techniques for Retention
Here are some proven methods for retaining definitions more effectively:
- Flashcards: Create flashcards with the term on one side and the definition on the other. Regularly reviewing them will help reinforce your memory.
- Visualization: Try to visualize the concept in action. For example, when learning about different shapes, draw them or picture them in your mind to help associate the definition with the image.
- Mnemonics: Use mnemonic devices to create memorable phrases or acronyms. For example, “SOH CAH TOA” is a well-known mnemonic for trigonometric ratios.
- Contextual Learning: Whenever possible, try to learn definitions through practical application. Solving real problems will help solidify the terms in your memory.
- Group Study: Teaching or discussing definitions with others can help you remember them better, as explaining concepts reinforces your understanding.
Staying Consistent with Review
Consistency is key when it comes to memorization. Set aside regular time each day to review the terms you’ve learned. Spacing out your review sessions over time–known as spaced repetition–has been shown to significantly improve long-term retention.
By incorporating these strategies into your study routine, you’ll be able to memorize and understand definitions more easily, making it easier to tackle complex problems when the time comes.
How to Tackle Word Problems in Mathematics
Word problems can often seem intimidating, especially when they involve complex figures and concepts. However, with the right approach, these problems can become more manageable. The key to solving word problems is to break them down into smaller, more understandable parts. By systematically identifying the information provided and determining what needs to be found, you can methodically work through the problem step by step.
The first step is always to read the problem carefully and identify the main elements. Highlight or underline the key pieces of information, such as numerical values, shapes, or relationships mentioned. Then, translate the verbal description into mathematical terms. This may involve drawing a diagram or labeling known values to visualize the situation more clearly. Once you’ve established the facts, you can begin applying the appropriate formulas and methods to find the solution.
Steps to Solve Word Problems Effectively
Follow these steps to approach word problems with confidence:
- Read the problem thoroughly: Make sure you understand what is being asked before attempting a solution.
- Identify known values: Extract all the relevant numerical data or relationships mentioned in the problem.
- Draw a diagram: Visualize the problem by sketching it. This helps clarify the relationships between the elements described in the problem.
- Write an equation: Convert the word problem into a mathematical expression or equation using the identified values and relationships.
- Solve step by step: Apply appropriate mathematical techniques and formulas to solve the equation.
- Check your work: Review the solution to ensure it makes sense in the context of the problem.
Common Pitfalls to Avoid
Word problems can be tricky, but avoiding a few common mistakes can help you solve them more easily:
- Misinterpreting the question: Always double-check what is being asked to avoid solving for the wrong quantity.
- Overlooking important details: Small pieces of information, such as units or conditions, can be crucial for solving the problem correctly.
- Rushing through the problem: Take your time to carefully analyze each part of the problem before jumping into a solution.
By following these strategies and remaining patient, you’ll be able to approach word problems with confidence and increase your chances of finding the correct solution.
Improving Your Accuracy in Mathematics

Achieving accuracy in solving mathematical problems is essential for success. Whether you’re working through equations, applying formulas, or solving for unknowns, precision makes a significant difference in your ability to obtain the correct results. Improving your accuracy requires attention to detail, careful calculations, and a systematic approach to problem-solving. By building strong habits and practicing regularly, you can enhance your ability to work through problems with greater confidence and correctness.
One of the most effective ways to improve accuracy is by slowing down and focusing on each step. Rushing through problems increases the likelihood of mistakes, while a methodical approach reduces errors and ensures that you don’t miss any important details. Double-checking your work and reviewing your steps before finalizing an answer also helps eliminate common mistakes, such as calculation errors or missed values.
Strategies for Enhancing Precision
Here are some strategies to help you improve your accuracy:
- Work in an organized manner: Break down problems into smaller steps and approach each one carefully. This prevents skipping important parts of the process.
- Use a consistent method: Stick to the same approach for similar problems. A standardized method helps you avoid confusion and makes it easier to spot mistakes.
- Check your calculations: Always verify your numbers. A small arithmetic error can lead to incorrect results, so reviewing your calculations can prevent that.
- Pay attention to units: Make sure you’re using the correct units throughout the process. Incorrect units can throw off an otherwise accurate solution.
- Practice regularly: The more you practice, the more familiar you’ll become with common patterns and approaches, helping to avoid errors.
Common Mistakes to Watch For
While working through problems, it’s helpful to be aware of some common pitfalls that can reduce your accuracy:
- Skipping steps: Omitting important steps in calculations or assumptions can lead to inaccurate solutions.
- Not simplifying expressions: Leaving complex expressions unsimplified or not fully reducing fractions may result in incorrect answers.
- Misinterpreting the problem: Be sure to read questions carefully to understand what’s being asked. Misinterpreting the problem often leads to errors in your approach.
By applying these strategies and practicing consistently, you can significantly improve your accuracy and approach mathematical problems with more confidence and skill.
Reviewing Past Assessments
One of the most effective ways to prepare for upcoming assessments is by reviewing previous evaluations. This practice not only familiarizes you with the types of problems you may encounter but also helps you identify common patterns and question formats. By analyzing past materials, you can better understand the areas where you need improvement and gain confidence in tackling similar challenges in the future.
Going over past assessments allows you to pinpoint recurring topics or concepts. These often represent key areas that will likely appear again, making it essential to understand them thoroughly. Additionally, reviewing your past work provides the opportunity to identify any mistakes made and learn from them, refining your problem-solving techniques for the next assessment.
How to Effectively Review Past Materials
- Revisit Mistakes: Focus on errors made in previous evaluations. Understand why you made them and what the correct approach should have been.
- Analyze Question Types: Take note of the types of problems asked. Understanding the format will help you know what to expect in future evaluations.
- Practice Similar Problems: After reviewing the mistakes and understanding the question format, practice solving similar problems to reinforce your skills.
- Focus on Key Areas: Pay extra attention to topics or concepts that appeared frequently. These are likely to be areas of emphasis in future evaluations.
- Take Time to Reflect: After reviewing, reflect on your overall understanding. Are there areas you still find challenging? Take time to address them through additional practice.
Maximizing Review Sessions
To get the most out of your review sessions, consider the following tips:
- Set Goals: Have specific objectives for each review session. Focus on mastering certain concepts or solving specific types of problems.
- Create a Schedule: Organize your review time to ensure you’re covering all important areas. Allocate more time to topics that need improvement.
- Work with a Study Partner: Reviewing with someone else can help clarify doubts and give you new perspectives on problem-solving techniques.
By carefully reviewing past evaluations, you can enhance your understanding of the material, improve your problem-solving abilities, and increase your chances of success in future assessments.
Why Practice Makes Perfect in Geometry
Repetition and consistent engagement with material are fundamental to mastering any subject. When it comes to mathematical concepts, especially those involving spatial reasoning and problem-solving, regular practice helps reinforce your understanding and improve your skills. The more you expose yourself to different types of problems, the more confident and proficient you become in applying the concepts you’ve learned.
By regularly working through challenges, you build muscle memory that allows you to recognize patterns, streamline your problem-solving process, and avoid common mistakes. Additionally, solving a variety of problems ensures that you are well-prepared for any scenario that might arise during an assessment or in real-life applications.
The Importance of Consistent Repetition
- Builds Confidence: The more you practice, the more confident you become in your ability to tackle unfamiliar problems.
- Identifies Weaknesses: Consistent practice helps reveal areas where you may need additional study or improvement.
- Increases Speed: Through repetition, you become faster at recognizing the right approach to solve a problem, which is crucial during timed evaluations.
How Regular Engagement Improves Understanding
Engaging with the material regularly helps to reinforce the concepts and theories behind each problem. As you solve more problems, you begin to internalize the rules and methods, making it easier to recall and apply them when needed. This ongoing process of exposure and application deepens your understanding and enhances your critical thinking abilities.
- Concept Mastery: Repeatedly applying the same concepts helps to ensure that you understand the material at a deeper level.
- Problem-Solving Skills: With each new problem, you refine your strategies for approaching and solving challenges effectively.
In conclusion, engaging regularly with the material is the key to mastering any field, especially one that requires critical thinking and analytical skills. Consistent practice not only helps you refine your abilities but also increases your confidence and efficiency in solving problems, leading to greater success in the long term.