
Understanding the fundamental principles of magnetism is essential for mastering this branch of physics. A variety of topics related to forces, fields, and energy need to be explored and applied. This section focuses on providing clarity and insight into the core concepts that frequently appear in assessments.
Students often encounter problems requiring a strong grasp of theoretical knowledge as well as the ability to solve practical problems. With a thorough understanding of the key principles, one can confidently approach tasks that involve fields, forces, and electromagnetic phenomena. This guide is designed to help reinforce that understanding and offer effective strategies for tackling related challenges.
Strengthening your grasp of these core ideas will greatly improve your ability to navigate through different types of assessments. Whether you’re dealing with theoretical questions or calculations, a solid foundation will make all the difference in achieving success.
Magnetic Forces and Field Problems
This section covers key challenges related to understanding and applying magnetic phenomena in various scenarios. Solving these problems requires a solid grasp of both theoretical concepts and practical skills. Students will encounter tasks involving the relationship between electric currents and magnetic fields, as well as calculations of forces exerted on objects within these fields.
Common Problem Types
One common problem type involves calculating the force experienced by a charged particle moving through a magnetic field. This requires knowledge of the particle’s charge, velocity, and the field strength. Another frequent challenge is determining the magnetic field strength around different configurations, such as coils or solenoids, which plays a crucial role in understanding real-world applications.
Effective Problem-Solving Strategies

To solve these problems efficiently, it is important to break them down into smaller, manageable steps. Begin by identifying the known variables and the required outcome. Then, apply the relevant formulas, such as the Lorentz force equation or Ampère’s law, to find the solution. With practice, the ability to quickly identify key factors and choose the right approach will improve significantly.
Understanding the Basics of Magnetism
At its core, the study of magnetic forces involves exploring the interactions between materials and invisible forces that arise from electric charges. These forces can attract or repel objects, and their strength depends on various factors, such as the distance between objects and the nature of the materials involved. Grasping these fundamental principles is key to understanding more complex concepts in physics.
One of the most important aspects is the concept of a field, which represents the area in which a magnetic force can act on objects. It is essential to understand how these fields are generated by moving charges and how they influence the behavior of different materials, such as iron or steel. This foundational knowledge sets the stage for delving deeper into more advanced topics.
Key Concepts in Electromagnetism
This section explores the essential principles that form the foundation of electromagnetism. Understanding how electric currents generate magnetic fields and how those fields interact with charged particles is crucial for solving related problems. These core ideas are the building blocks for more complex applications and phenomena in physics.
Electromagnetic Fields
Electromagnetic fields are created by the movement of charged particles. These fields play a central role in the interaction between electricity and magnetism. Key points to understand include:
- How a moving charge generates a magnetic field around it
- The relationship between electric currents and magnetic fields
- The concept of field lines, which represent the direction and strength of a magnetic field
Important Laws in Electromagnetism
Several fundamental laws govern the behavior of electric and magnetic fields. These laws are crucial for solving problems and predicting the behavior of systems. Some key laws include:
- Faraday’s Law of Induction – Describes how a changing magnetic field induces an electric current.
- Ampère’s Law – Explains the relationship between electric currents and the magnetic fields they create.
- Gauss’s Law – Relates the electric flux through a closed surface to the charge enclosed within it.
Common Magnetism Challenges in Assessments
In many assessments, students encounter problems that test their understanding of fundamental concepts related to magnetic forces and fields. These challenges often require applying formulas, interpreting diagrams, or solving complex scenarios involving interactions between electric currents and magnetic materials. Mastery of these topics is essential for success in solving real-world problems and understanding advanced concepts.
Force Calculation Problems

One of the most frequent problem types involves calculating the force exerted on a charged particle or current-carrying conductor placed in a magnetic field. Typical problems require students to use equations like the Lorentz force formula or the equation for the force on a current-carrying wire. Common steps in these problems include:
- Identifying the magnetic field strength and direction
- Determining the velocity or current in the system
- Applying the correct formula to calculate the force
Magnetic Field Calculations

Another common challenge involves determining the magnetic field strength at a specific point. These problems may require using formulas like the Biot-Savart law or Ampère’s law. In such problems, students must consider factors such as:
- The configuration of the current-carrying conductor (e.g., straight wire, loop, or solenoid)
- The distance from the point where the field is being measured
- The magnitude and direction of the current or charge
Answering Magnetic Field Calculation Problems
Calculating the strength of a magnetic field is a key aspect of solving problems in this area of physics. These tasks often require applying specific formulas based on the configuration of the system, such as the current-carrying conductors or the charged particles involved. A solid understanding of the fundamental principles behind magnetic fields allows for a systematic approach to these calculations.
Key Formulas for Magnetic Field Calculations
Several formulas are essential for calculating the magnetic field in various situations. Some of the most commonly used include:
- Biot-Savart Law: Used to determine the magnetic field produced by a small segment of current-carrying wire.
- Ampère’s Law: Helps calculate the magnetic field around a loop of current or along straight conductors.
- Magnetic Field of a Solenoid: Describes the strength of the magnetic field inside a long coil of wire carrying an electric current.
Step-by-Step Problem Solving
To tackle these calculations, follow a structured approach:
- Identify the configuration of the system, such as the shape of the wire or the placement of the current.
- Determine the relevant variables, such as current, distance, and geometry of the system.
- Choose the appropriate formula based on the problem’s requirements.
- Substitute the known values and solve for the magnetic field strength.
By carefully working through each step, even complex problems can be solved effectively.
Types of Magnets and Their Properties
There are several distinct types of magnets, each exhibiting unique properties depending on their material composition and how they are magnetized. Understanding these types is crucial for determining how they interact with other objects and materials. The behavior of magnets plays a central role in various technological applications, from electric motors to magnetic storage devices.
Magnets can be broadly categorized into three main types: permanent, temporary, and electromagnets. Each type differs in its ability to retain magnetic properties, the strength of its magnetic field, and its response to external forces or electric currents.
Permanent magnets are materials that retain their magnetism over time without requiring an external power source. These are commonly used in everyday objects such as fridge magnets or compasses. Temporary magnets, on the other hand, only exhibit magnetic properties when placed in a magnetic field, losing their magnetism once the field is removed. Electromagnets are created by passing an electric current through a coil of wire, generating a magnetic field that can be turned on and off by controlling the current.
Magnetic Forces and Their Effects
The invisible forces created by moving charges or current-carrying conductors play a fundamental role in many physical phenomena. These forces can attract or repel objects depending on their properties and the surrounding field. Understanding the nature and effects of these forces is essential for analyzing the behavior of charged particles and conducting systems.
Force Between Magnetic Poles
One of the most basic effects of magnetic forces is the interaction between magnetic poles. Like poles repel each other, while opposite poles attract. This principle is crucial in understanding the behavior of permanent magnets and the structure of magnetic fields. The force between two poles depends on their strength and the distance between them, following an inverse square law similar to gravitational attraction.
Force on a Moving Charge
When a charged particle moves through a magnetic field, it experiences a force that is perpendicular to both its velocity and the direction of the magnetic field. This interaction is described by the Lorentz force law. The magnitude of this force depends on factors such as the charge of the particle, its velocity, and the strength of the magnetic field. This principle is fundamental in the design of devices like electric motors and generators.
Application of Magnetic Fields in Real Life
The invisible forces generated by electric currents and magnetic materials have a wide range of practical applications in everyday life. From transportation to communication, the effects of magnetic fields are integral to many modern technologies. Understanding how these fields are harnessed can provide insight into how they shape various industries and scientific advancements.
One of the most common applications is in electric motors, where magnetic fields are used to convert electrical energy into mechanical movement. These motors are found in numerous devices, from household appliances like fans and washing machines to larger systems such as electric cars and industrial machinery.
Another key application is in medical imaging. Magnetic resonance imaging (MRI) uses powerful magnetic fields to produce detailed images of the inside of the body, allowing doctors to diagnose various conditions without the need for invasive procedures. This non-invasive technology has revolutionized healthcare by providing accurate diagnostics and improving patient care.
In addition, magnetic fields are essential for data storage and retrieval in computers and other electronic devices. Hard drives rely on the magnetic properties of materials to store digital information, while magnetic fields are also used in devices such as credit cards, barcode scanners, and speakers.
Magnetic Induction and Its Significance
The process by which a changing magnetic field induces a current in a conductor is a fundamental phenomenon with wide-ranging applications in modern technology. This effect, often referred to as electromagnetic induction, plays a pivotal role in the generation of electricity and the functioning of numerous devices. It forms the basis for many systems that power our daily lives, from electric generators to transformers.
Principles of Induction
Electromagnetic induction occurs when a conductor, such as a wire, is exposed to a changing magnetic field. This change induces an electromotive force (EMF), which can drive a current through the conductor. The magnitude of the induced current depends on factors such as the rate of change of the magnetic field, the strength of the field, and the properties of the conductor itself.
Applications in Real-World Technology
Induction is the core principle behind many devices used in power generation, energy transfer, and signal processing. Below is a summary of some of the key applications:
| Application | Function |
|---|---|
| Electric Generators | Convert mechanical energy into electrical energy by rotating a coil in a magnetic field. |
| Transformers | Alter voltage levels in AC circuits by inducing a magnetic field in a coil. |
| Induction Motors | Use electromagnetic induction to generate rotational motion for various industrial applications. |
| Wireless Charging | Use induction to transfer energy between coils for charging devices without direct contact. |
Understanding the process of magnetic induction is essential for developing more efficient systems for energy generation, transfer, and consumption. Its applications continue to expand, paving the way for advancements in renewable energy, electronics, and communication technologies.
Exploring the Right-Hand Rule
The right-hand rule is a simple yet powerful concept used to determine the direction of various vector quantities in the context of electric currents and magnetic fields. It provides a way to visualize the interaction between currents, magnetic fields, and forces in three-dimensional space. Understanding this rule is crucial for solving problems related to forces on moving charges and current-carrying conductors.
This rule is used in several different contexts, with each variation providing insight into different aspects of electromagnetism. Below are the key applications of the right-hand rule:
- Force on a Current-Carrying Conductor: When a current flows through a conductor in a magnetic field, the direction of the force on the conductor can be found by using the right-hand rule. Point the thumb of your right hand in the direction of the current, and curl your fingers in the direction of the magnetic field. Your palm will face the direction of the force exerted on the conductor.
- Magnetic Field Around a Current: To find the direction of the magnetic field created by a current-carrying conductor, hold your right hand so that your thumb points in the direction of the current. The curl of your fingers will show the direction of the magnetic field surrounding the wire.
- Force on a Moving Charge: For a moving charged particle in a magnetic field, the direction of the force can be determined by pointing the fingers of your right hand in the direction of the particle’s velocity, with your palm facing the magnetic field. The direction your thumb points indicates the force on the particle, given that the charge is positive. For a negative charge, the force direction will be opposite.
By consistently applying the right-hand rule, it becomes easier to visualize the relationships between electric currents, magnetic fields, and the forces they produce. This method is indispensable in both theoretical studies and practical applications in physics and engineering.
Magnetism and Electric Current Relationship
The interaction between electric currents and magnetic fields is a fundamental concept in physics. When an electric current flows through a conductor, it generates a surrounding field, a property that is central to many technological devices and natural phenomena. This connection between electricity and magnetic effects is the foundation for much of modern electrical engineering and electromagnetism.
The Formation of Magnetic Fields by Current
One of the key principles in this relationship is that an electric current creates a magnetic field around the conductor. This can be observed in simple experiments, such as when a current-carrying wire is placed near a compass, causing the needle to deflect. The strength of the magnetic field depends on factors like the amount of current flowing and the distance from the conductor.
Applications of This Relationship
Understanding the relationship between electric currents and magnetic fields has led to numerous applications in everyday life. Some of the most notable include:
- Electric Motors: By creating a magnetic field around a current-carrying coil, motors are able to produce rotational movement, which is used in countless machines from household appliances to industrial equipment.
- Transformers: These devices use alternating current to generate changing magnetic fields, which then induce a voltage in another coil, allowing for efficient transmission of electricity across long distances.
- Electromagnets: By winding wire into coils and passing current through them, electromagnets are created, which can be turned on or off depending on whether current is flowing, making them versatile in many applications like cranes and MRI machines.
The connection between electric current and the generated field is vital in both theoretical understanding and practical innovations. This relationship continues to drive advances in technology, from power generation to medical devices.
Solving Problems Involving Magnetic Flux

Magnetic flux is a concept used to quantify the strength and direction of a magnetic field passing through a given area. It is a key quantity in understanding how magnetic fields interact with materials and how they can induce electrical currents. Solving problems that involve this concept requires an understanding of how to calculate the flux and interpret its effects in various situations.
The general formula for magnetic flux is:
Φ = B × A × cos(θ)
Where:
- Φ is the magnetic flux, measured in Webers (Wb).
- B is the magnetic field strength, measured in Teslas (T).
- A is the area through which the field lines pass, measured in square meters (m²).
- θ is the angle between the magnetic field lines and the normal to the surface (perpendicular to the area).
To solve problems involving flux, follow these steps:
- Determine the Magnetic Field Strength: Identify the magnetic field in the problem. This could be given directly or inferred from other information, such as the force on a moving charge or the current in a wire.
- Identify the Area: Find the area through which the field passes. In many cases, this may involve geometric shapes like circles or rectangles.
- Account for the Angle: If the magnetic field is not perpendicular to the surface, calculate the angle between the field lines and the surface. The cosine of this angle determines how much of the magnetic field contributes to the flux.
- Calculate the Flux: Use the formula to compute the flux, plugging in the values for magnetic field strength, area, and angle.
By applying this method, you can solve a wide range of problems related to magnetic fields and their effects. This concept is crucial for understanding how electromagnetic devices, such as generators and transformers, work in practical applications.
Key Formulas for Magnetism Questions

When dealing with problems related to magnetic fields, several key equations are essential for calculating various properties and understanding their effects. These formulas allow for precise calculations in fields ranging from simple magnetic interactions to complex electromagnetic applications. Mastering these equations is crucial for solving related problems efficiently.
Magnetic Field Strength

The magnetic field strength at a point is often calculated using the formula:
B = μ₀ * (I / 2πr)
Where:
- B is the magnetic field strength in Teslas (T).
- μ₀ is the permeability of free space (4π × 10⁻⁷ T·m/A).
- I is the current passing through the conductor, measured in amperes (A).
- r is the distance from the wire to the point where the magnetic field is measured, in meters (m).
Magnetic Flux
To calculate magnetic flux, the formula to use is:
Φ = B * A * cos(θ)
Where:
- Φ is the magnetic flux in Webers (Wb).
- B is the magnetic field strength in Teslas (T).
- A is the area through which the magnetic field passes, in square meters (m²).
- θ is the angle between the magnetic field and the surface normal.
These formulas provide a foundation for calculating fundamental quantities like the magnetic field and flux. Understanding and applying them properly will enable you to solve a wide variety of related problems.
Understanding Magnetic Domains and Materials
In the study of materials that respond to magnetic fields, it is important to understand the role of internal structures, such as domains, and how these materials behave under different conditions. The alignment and movement of these structures determine the overall magnetic properties of a substance, influencing its use in various applications, from electronics to engineering.
Magnetic domains are small regions within a material where the magnetic moments of atoms are aligned in the same direction. When these domains are aligned uniformly, the material becomes magnetized. Conversely, when the domains are misaligned, the material does not exhibit noticeable magnetic properties. The key factor in changing this alignment is external influence, such as the application of a magnetic field.
Types of Magnetic Materials
Materials can be broadly categorized based on how they interact with magnetic fields:
- Ferromagnetic materials: These materials have strong interactions with magnetic fields, allowing them to become permanently magnetized. Examples include iron, cobalt, and nickel.
- Paramagnetic materials: These materials are weakly attracted to magnetic fields and do not retain magnetic properties once the external field is removed. Aluminum and platinum are examples.
- Diamagnetic materials: These materials are repelled by magnetic fields and exhibit weak negative magnetism. Examples include copper and bismuth.
Applications of Magnetic Materials
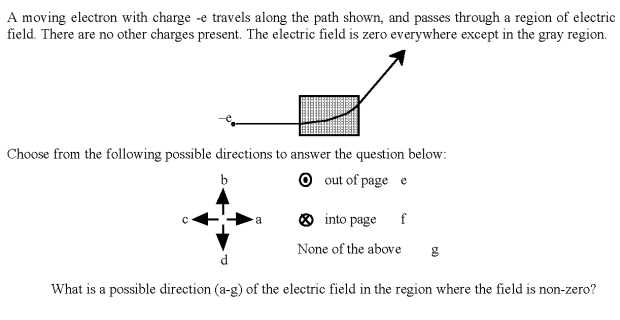
The properties of these materials are utilized in a wide range of technologies. For example, ferromagnetic substances are essential in creating permanent magnets used in motors, magnetic storage devices, and medical imaging equipment. Meanwhile, paramagnetic and diamagnetic materials are often employed in specialized applications like magnetic levitation and superconducting systems.
Frequently Asked Questions in Magnetism Exams
When preparing for assessments on the topic of magnetic forces and fields, certain concepts tend to come up repeatedly. Understanding these concepts and their applications is essential for mastering the subject. Here, we will explore some of the most common inquiries and provide insights into how to approach them effectively.
Common Areas of Focus
Below are a few of the key topics that often appear in assessments related to magnetic forces and their properties:
- The relationship between electric current and magnetic fields: Students frequently need to understand how a moving charge generates a magnetic field and how the direction of this field can be determined.
- Magnetic field strength and its calculation: Many questions involve calculating the strength of a magnetic field based on variables like current, distance, and geometry.
- Forces on moving charges: Problems often ask how to calculate the force exerted on a charged particle moving through a magnetic field.
- Applications of magnetic materials: Understanding the practical uses of different materials, such as ferromagnetic, paramagnetic, and diamagnetic substances, is also a common theme.
Effective Strategies for Success
To tackle these challenges, it’s essential to apply systematic approaches:
- Master key formulas: Review important equations that govern magnetic forces, such as the Lorentz force law and Ampère’s law, to ensure you can apply them confidently.
- Understand vector directions: Pay attention to the direction of magnetic fields and forces, often determined using rules like the right-hand rule or the left-hand rule.
- Practice problem-solving: Regularly solve practice problems to improve your ability to apply theoretical concepts to practical scenarios.
By focusing on these areas, you will be better equipped to tackle the most common challenges in any assessment related to magnetic forces and fields.
How to Approach Magnetism Theory Questions

When tackling theoretical problems related to magnetic fields and forces, it’s crucial to develop a systematic approach. These types of problems often require a deep understanding of core concepts and the ability to apply them to different scenarios. Focusing on key principles and ensuring clarity in your reasoning are essential for success.
Breaking Down the Problem
Start by carefully reading the question and identifying what is being asked. Pay attention to any given values or conditions, such as the type of material or the configuration of the system. Often, these problems will test your understanding of basic principles, so take note of:
- Key concepts: Determine which laws or principles are relevant to the problem (e.g., the Biot-Savart law or Faraday’s law).
- Given information: Look for numerical data, angles, or distances that will help you calculate the required values.
- What needs to be found: Clarify the main objective of the problem – whether it’s the direction of a force, the magnitude of a field, or the behavior of a current.
Step-by-Step Problem Solving
Once you have a clear understanding of the question, break it down into manageable steps:
- Apply the relevant equations: Use the appropriate formulas for the specific situation. Don’t forget to adjust units and include any constants that may apply.
- Visualize the problem: Often, drawing a diagram of the setup can help clarify the relationships between different elements, like the direction of current or the orientation of a field.
- Check your work: After solving the problem, review each step to ensure all assumptions are valid and that your solution aligns with the problem’s conditions.
By following these strategies, you’ll be well-prepared to confidently approach theoretical problems in this field.
Tips for Magnetism Multiple-Choice Questions

When approaching multiple-choice problems in topics related to magnetic fields and forces, it’s important to have a strategy to maximize your chances of success. These types of problems often offer several possible answers, and having a clear approach can help you navigate them more efficiently. Focus on narrowing down options, eliminating incorrect answers, and applying fundamental principles.
Strategy for Success
Before diving into calculations or detailed reasoning, follow these tips to increase your accuracy:
- Read the question carefully: Ensure you fully understand what is being asked. Look for keywords and important details that might direct you toward the right choice.
- Analyze all answer choices: Review every option before making a decision. Sometimes, one answer may be partially correct, but others are more precise.
- Eliminate obviously wrong choices: If any options seem unrealistic or do not fit the context of the problem, rule them out first to improve your odds.
- Check units and magnitudes: Ensure that your answer has the correct units and falls within a reasonable range, based on the given information.
Efficient Problem-Solving
Once you’ve reviewed the options, consider these additional approaches:
- Use the process of elimination: If you can rule out two or more choices, the remaining options become easier to evaluate.
- Apply basic principles: For each answer, quickly think through the core concepts that are relevant. Which one aligns best with known laws or the setup of the problem?
- Manage your time: If you’re unsure, move on to the next problem and come back later. Don’t get stuck on one question for too long.
By following these strategies, you can boost your confidence and enhance your ability to solve multiple-choice problems related to magnetic concepts.
Reviewing Magnetism for Exam Success
To achieve success in tests involving the study of magnetic fields and forces, it’s crucial to develop a comprehensive understanding of core concepts. A structured review can help solidify your knowledge and improve problem-solving skills. By revisiting key principles, performing practice exercises, and focusing on weak areas, you can ensure a strong performance when it matters most.
Effective Review Strategies
Adopting the right review techniques can significantly enhance your ability to recall information and solve problems accurately. Consider the following approaches:
- Focus on core concepts: Make sure to understand the fundamental theories and equations related to the behavior of magnetic fields, forces, and related phenomena.
- Practice with different types of problems: Regularly solving a variety of practice problems helps reinforce the application of theoretical knowledge in different contexts.
- Identify weak points: Pay special attention to the areas where you struggle the most. Devote extra time to these topics to gain confidence and mastery.
- Use diagrams and visual aids: Visualizing the direction of forces, field lines, and other concepts helps you understand and remember them better.
Key Topics to Review
Make sure to cover the following essential topics during your review sessions:
| Topic | Key Concepts |
|---|---|
| Magnetic Fields | Field lines, strength, and direction |
| Electromagnetic Induction | Faraday’s Law, Lenz’s Law, induced voltage |
| Forces on Moving Charges | Lorentz force, right-hand rule |
| Applications | Electric motors, generators, transformers |
By focusing on these areas and utilizing structured review techniques, you’ll be better prepared to tackle any challenges that arise during your assessment.