
As you approach the end of your course, it’s essential to consolidate your knowledge and strengthen your understanding of the key concepts covered. This assessment will test your ability to apply various mathematical techniques and solve problems efficiently under pressure. Reviewing the material thoroughly will ensure you’re ready to tackle the challenges ahead with confidence.
In the following sections, we will explore the most important topics to focus on, strategies to enhance your problem-solving skills, and tips for managing time effectively during the test. A systematic approach to preparation will help you feel more in control and increase your chances of achieving a strong result.
Be sure to practice consistently, review your notes, and seek clarification on any areas that remain unclear. This approach will set you up for success as you head into the assessment period. Focus on understanding the concepts rather than memorizing answers, and you’ll be well-equipped to perform your best.
Algebra 2 Semester 2 Final Exam Guide
Preparing for the upcoming assessment requires a deep understanding of core mathematical principles and a solid approach to problem-solving. Mastery of the concepts covered during this period will be tested in various formats, requiring a blend of both theoretical knowledge and practical application. Effective preparation involves reviewing key topics, practicing problem-solving techniques, and honing your ability to apply learned strategies under timed conditions.
Key Topics to Focus On
Ensure you thoroughly understand topics such as quadratic functions, polynomial operations, and systems of equations. Be prepared to work with radical expressions, logarithmic functions, and exponential growth. Each area will present different challenges, but with targeted practice, you can strengthen your ability to recognize patterns and solve problems efficiently. Pay close attention to the problem-solving methods used in class and review sample exercises that cover a wide range of question types.
Effective Study Strategies

Creating a structured study schedule is essential for tackling this material. Break down complex concepts into manageable parts and focus on one topic at a time. Use practice tests to simulate the actual conditions you’ll face, ensuring you’re familiar with the format and time constraints. Additionally, review any mistakes made during practice sessions and revisit those topics to reinforce understanding. Seeking clarification on confusing points can make a significant difference in your overall performance.
Key Concepts to Review
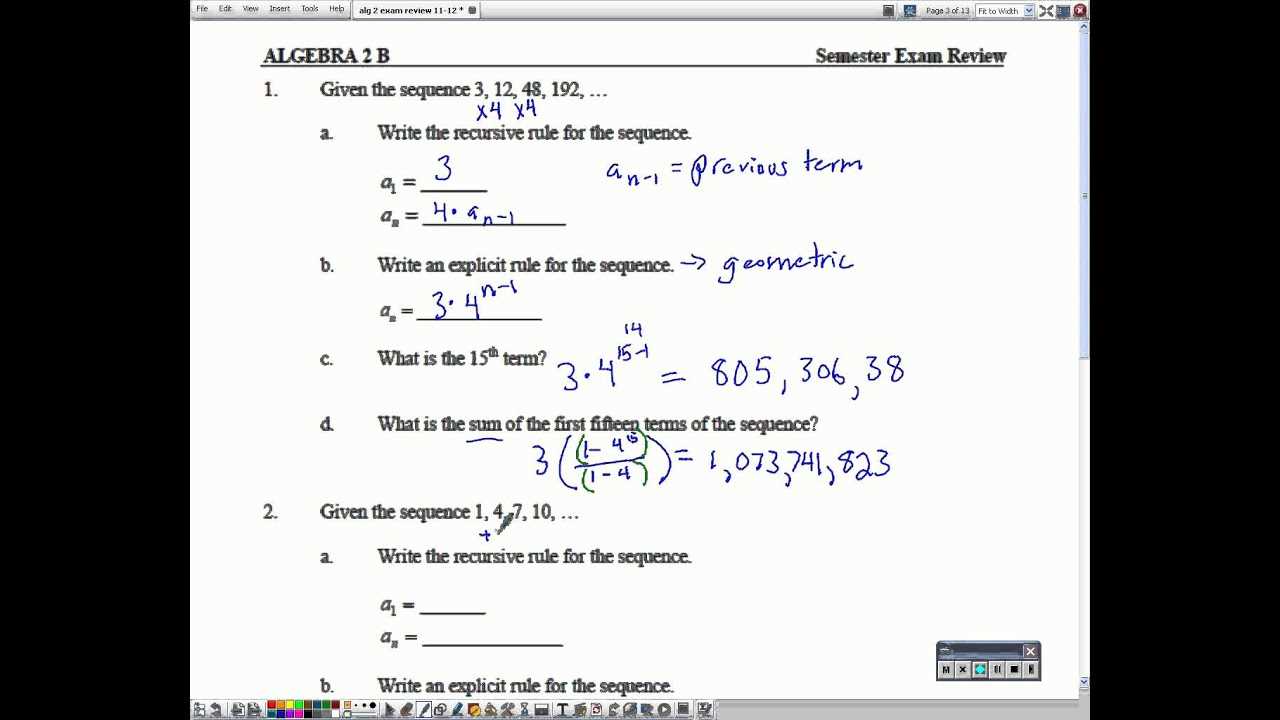
To succeed in the upcoming assessment, it’s crucial to revisit the fundamental principles covered throughout the course. A solid understanding of core topics will help you navigate complex problems with ease and apply the right methods when needed. Focusing on these key concepts will ensure you’re well-prepared and can approach any question with confidence.
Understanding Functions and Their Properties
Make sure you’re comfortable working with different types of functions, including quadratics, polynomials, and rational expressions. Review their graphs, key characteristics, and transformations. Practice solving for the roots of functions, finding intercepts, and understanding how changes in the function’s equation affect its graph. These are essential skills that will appear frequently throughout the assessment.
Mastering Systems of Equations and Inequalities
Equations and inequalities often appear in multiple forms during the assessment. Practice solving systems of equations using substitution and elimination methods. Review solving and graphing linear and non-linear inequalities, as well as understanding how to interpret the solution sets. Having a strong grasp of these techniques will allow you to efficiently solve a wide range of problems.
Understanding Quadratic Equations
Quadratic equations are a critical area to master as they frequently appear in various forms and problems. These equations typically involve variables raised to the second power and can be solved using a variety of methods. Understanding how to manipulate and solve them will give you a solid foundation for tackling related problems in the assessment.
There are several methods for solving quadratic equations, each useful depending on the context. Here are the most common approaches:
- Factoring: Express the equation as a product of binomials, and then solve for the variable.
- Quadratic Formula: Use the formula x = (-b ± √(b² – 4ac)) / 2a to solve equations in standard form.
- Completing the Square: Transform the equation into a perfect square trinomial, and then solve for the variable.
Each method requires practice to apply effectively, so be sure to solve a variety of problems using each approach. Additionally, understanding the graph of a quadratic function and its key features–such as the vertex and axis of symmetry–will enhance your ability to interpret and solve related problems. Knowing how to find the solutions, whether real or complex, is an essential skill.
Mastering Polynomial Functions
Polynomial functions are an essential component of advanced mathematics, and having a firm grasp on how to work with them will significantly improve your problem-solving skills. These functions involve terms with variables raised to different powers, and they can be represented in a variety of forms. Whether you’re factoring, solving, or graphing these functions, a thorough understanding of their properties will be invaluable during your assessment.
Key Concepts to Review
- Degree and Leading Coefficient: The degree of a polynomial is determined by the highest power of the variable, and the leading coefficient is the number multiplying this term. These factors influence the graph’s shape and behavior.
- Roots and Zeros: Find the solutions to polynomial equations by determining the values of the variable that make the polynomial equal to zero. These are the points where the graph intersects the x-axis.
- End Behavior: Understand how the graph of a polynomial behaves as the variable approaches positive or negative infinity, depending on the degree and leading coefficient.
Methods for Solving Polynomial Equations
- Factoring: Factor polynomials to find the roots. Look for common factors, use the difference of squares, or apply grouping.
- Using the Rational Root Theorem: This method helps identify possible rational solutions to a polynomial equation by considering the factors of the constant term and the leading coefficient.
- Synthetic Division: A faster method for dividing polynomials, especially useful when dividing by a linear factor.
As you prepare, practice solving polynomial functions using these methods and pay attention to the specific characteristics of each polynomial type. Mastery of these techniques will make you more efficient in recognizing patterns and solving complex problems quickly.
Graphing Rational Expressions
Graphing rational expressions requires an understanding of how the numerator and denominator influence the overall shape and behavior of the graph. These functions can exhibit unique characteristics, such as vertical and horizontal asymptotes, holes, and intercepts. Being able to analyze and graph these expressions will help you visually interpret the function’s behavior and solve related problems effectively.
The first step in graphing rational expressions is to identify key features of the function:
- Vertical Asymptotes: These occur where the denominator equals zero, and the function approaches infinity or negative infinity. They represent values of the variable that the function cannot take.
- Horizontal Asymptotes: These indicate the behavior of the graph as the variable approaches very large or very small values. The function may approach a constant value depending on the degree of the numerator and denominator.
- Holes: Holes occur where both the numerator and denominator have a common factor that cancels out. The hole represents a missing point on the graph.
- Intercepts: Find the x-intercepts by setting the numerator equal to zero, and the y-intercept by evaluating the function when the variable is zero.
Once you’ve identified these key features, you can plot them on the coordinate plane and sketch the graph. Remember that rational functions can have multiple sections with different behaviors depending on the asymptotes and intercepts. By carefully analyzing these features and using them to guide your graphing process, you’ll be able to create accurate representations of rational expressions.
Tips for Solving Systems of Equations
Solving systems of equations involves finding values for the variables that satisfy all equations in the system simultaneously. These problems can arise in various forms, including linear equations, inequalities, and other mathematical models. Developing strategies to efficiently solve these systems will help you approach them with confidence and precision.
There are several methods to consider when solving systems of equations:
- Substitution Method: Solve one equation for one variable and substitute this expression into the other equation. This method works well when one of the equations is easily solvable for a single variable.
- Elimination Method: Add or subtract the equations to eliminate one variable. This approach is useful when the coefficients of one variable are already aligned in both equations.
- Graphing Method: Plot both equations on the same graph and identify the point(s) where they intersect. This method gives a visual representation of the solution but may be less precise unless done carefully.
In addition to these methods, be mindful of certain techniques that can make solving systems more efficient:
- Look for Special Cases: Sometimes, the system may have no solution (parallel lines) or an infinite number of solutions (identical equations). Recognizing these cases early can save time.
- Work Step-by-Step: Solve one part of the system completely before moving on to the next. This helps maintain clarity and prevents mistakes.
- Check Your Solutions: Always substitute your solution back into the original equations to verify its accuracy. This ensures that no errors were made during the process.
By practicing these techniques and recognizing when to use each method, you’ll be able to solve systems of equations more quickly and accurately.
Working with Exponents and Radicals
Understanding the rules for working with exponents and radicals is fundamental for solving a wide range of mathematical problems. These concepts allow you to simplify expressions, solve equations, and manipulate formulas more efficiently. By mastering the properties of exponents and radicals, you’ll be able to approach complex problems with confidence and precision.
Rules for Exponents
Exponents are used to represent repeated multiplication. The key to working with exponents is understanding the rules that govern their operations. Here are some important properties to remember:
| Rule | Description | Example |
|---|---|---|
| Product of Powers | When multiplying two powers with the same base, add the exponents. | am × an = am+n |
| Power of a Power | When raising a power to another power, multiply the exponents. | (am)n = am×n |
| Power of a Product | When raising a product to a power, apply the exponent to each factor. | (ab)n = an × bn |
| Zero Exponent | Any nonzero number raised to the power of zero equals one. | a0 = 1 |
Working with Radicals
Radicals involve finding the root of a number, such as square roots or cube roots. Radicals are closely related to exponents, as the square root of a number is the same as raising that number to the power of 1/2. Here are some key properties and examples:
- Product Rule: The square root of a product is the product of the square roots: √(a × b) = √a × √b.
- Quotient Rule: The square root of a quotient is the quotient of the square roots: √(a / b) = √a / √b.
- Rationalizing the Denominator: When a radical appears in the denominator, multiply both the numerator and denominator by an appropriate radical to eliminate it.
By applying these rules and practicing different types of problems, you will become more efficient in simplifying and solving equations involving exponents and radicals.
Reviewing Logarithmic Functions

Logarithmic functions are the inverse of exponential functions and are vital for solving equations involving exponents. Understanding the relationship between these functions allows for effective manipulation of expressions and solving complex problems. Mastering the key properties and techniques for solving logarithmic equations will improve both your problem-solving skills and your ability to simplify expressions.
Key Properties of Logarithms
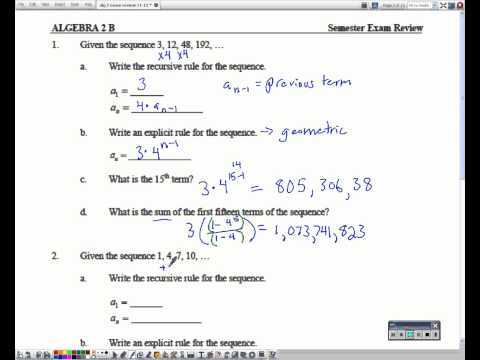
Logarithms have several important properties that simplify calculations and allow you to solve equations more efficiently. Here are the key properties to keep in mind:
- Product Rule: The logarithm of a product is the sum of the logarithms: logb (x * y) = logb (x) + logb (y).
- Quotient Rule: The logarithm of a quotient is the difference of the logarithms: logb (x / y) = logb (x) – logb (y).
- Power Rule: The logarithm of a power is the exponent times the logarithm: logb (xn) = n * logb (x).
- Change of Base Formula: If you need to evaluate a logarithm with a different base, use: logb (x) = loga (x) / loga (b).
Solving Logarithmic Equations
To solve logarithmic equations, it’s essential to apply the properties mentioned above and transform the equation into an exponential form. Here are some techniques for solving these types of equations:
- Isolate the Logarithm: If the logarithmic term is not isolated, begin by isolating it on one side of the equation. This simplifies the process and makes it easier to solve.
- Convert to Exponential Form: Use the fact that logb (x) = y is equivalent to by = x to convert the equation into an exponential form.
- Check for Extraneous Solutions: After solving, substitute the solution back into the original equation to check for any extraneous solutions, particularly when the domain of the logarithmic function is restricted.
By practicing these techniques and becoming familiar with logarithmic properties, you will be able to approach problems involving logarithmic functions with ease and accuracy.
Important Trigonometric Identities
Trigonometric identities are essential tools for simplifying expressions and solving equations in various mathematical contexts. These relationships between trigonometric functions provide a foundation for working with angles, triangles, and periodic functions. Understanding and applying these identities can make solving problems in trigonometry much more manageable and efficient.
Fundamental Trigonometric Identities
The most fundamental trigonometric identities form the basis for most trigonometric manipulations. These include the basic Pythagorean identity, reciprocal identities, and quotient identities:
- Pythagorean Identity: sin2(θ) + cos2(θ) = 1
- Reciprocal Identities:
- csc(θ) = 1/sin(θ)
- sec(θ) = 1/cos(θ)
- cot(θ) = 1/tan(θ)
- Quotient Identities:
- tan(θ) = sin(θ)/cos(θ)
- cot(θ) = cos(θ)/sin(θ)
Sum and Difference Identities

These identities are particularly useful when working with angles that are sums or differences of other angles. They allow for the simplification of expressions involving trigonometric functions of combined angles:
- Sum of Angles:
- sin(A + B) = sin(A)cos(B) + cos(A)sin(B)
- cos(A + B) = cos(A)cos(B) – sin(A)sin(B)
- tan(A + B) = (tan(A) + tan(B)) / (1 – tan(A)tan(B))
- Difference of Angles:
- sin(A – B) = sin(A)cos(B) – cos(A)sin(B)
- cos(A – B) = cos(A)cos(B) + sin(A)sin(B)
- tan(A – B) = (tan(A) – tan(B)) / (1 + tan(A)tan(B))
By becoming familiar with these identities and practicing their application, you’ll be able to simplify complex expressions and solve trigonometric equations more effectively.
Preparing for Word Problems

Word problems can often seem challenging, but with the right approach, they become much easier to tackle. The key to solving these types of problems lies in translating the real-world scenario into a mathematical equation that can be solved using the techniques you’ve learned. By carefully reading the problem, identifying the variables, and breaking the problem into smaller steps, you can systematically solve even the most complex questions.
Understanding the Problem
The first step in solving any word problem is understanding what is being asked. Pay close attention to the details provided and try to visualize the situation. Break the problem down into its components, identifying the known and unknown quantities. This will help you figure out what equations or operations you need to apply to find the solution.
- Identify key information: Look for numbers, units, and relationships between quantities.
- Define variables: Assign a variable to each unknown quantity to make the problem easier to solve.
- Determine what is being asked: Is the problem asking for a total, a rate, a difference, or something else?
Setting Up and Solving the Equation
Once you’ve understood the problem and identified the necessary information, it’s time to set up an equation. This step involves translating the relationships described in the problem into mathematical terms. Once the equation is set up, apply the appropriate mathematical methods to solve it. Here are some tips for solving the equation:
- Use the correct operations: Depending on the problem, you might need to use addition, subtraction, multiplication, or division, or even a combination of these operations.
- Check for units: Ensure that the units in your calculations match, and convert them if necessary to avoid mistakes.
- Double-check your work: After solving, revisit the problem and ensure that your solution makes sense in the context of the scenario.
By practicing these strategies, you’ll be better equipped to handle word problems and develop a more systematic approach to problem-solving.
Time Management on Exam Day
Managing your time effectively during an assessment is crucial for ensuring that you complete all sections within the allotted time frame. Without a solid plan, it’s easy to rush through some problems while spending too much time on others, leaving less time for more challenging questions. Developing a strategy for time allocation can help you approach the test with confidence, allowing you to answer as many questions as possible and reduce stress.
Planning Your Time

The first step is to allocate time to different sections of the test based on the number of questions and the difficulty level of each part. Prioritize questions that you are most comfortable with and save more challenging ones for later. Keeping track of time during the assessment will ensure that you do not spend too long on any one section.
| Section | Estimated Time | Strategy |
|---|---|---|
| Short Answer | 15 minutes | Quickly solve easy problems, mark more difficult ones to return to later. |
| Word Problems | 20 minutes | Carefully read each problem, define variables, solve step by step. |
| Longer Problems | 30 minutes | Break down into manageable parts, do the easier steps first. |
| Review | 10 minutes | Go over answers, double-check calculations, ensure all questions are addressed. |
Staying on Track
While working through the test, it’s important to monitor your progress regularly. Keep an eye on the clock and check your pacing to ensure that you’re not spending too much time on any one section. If you encounter a particularly difficult question, make a note to revisit it later and move on to the next one. This approach will prevent you from getting stuck and running out of time before completing the entire test.
By following these time management strategies, you can approach your assessment with a clear plan, stay organized, and maximize your chances of performing well under pressure.
Common Mistakes to Avoid
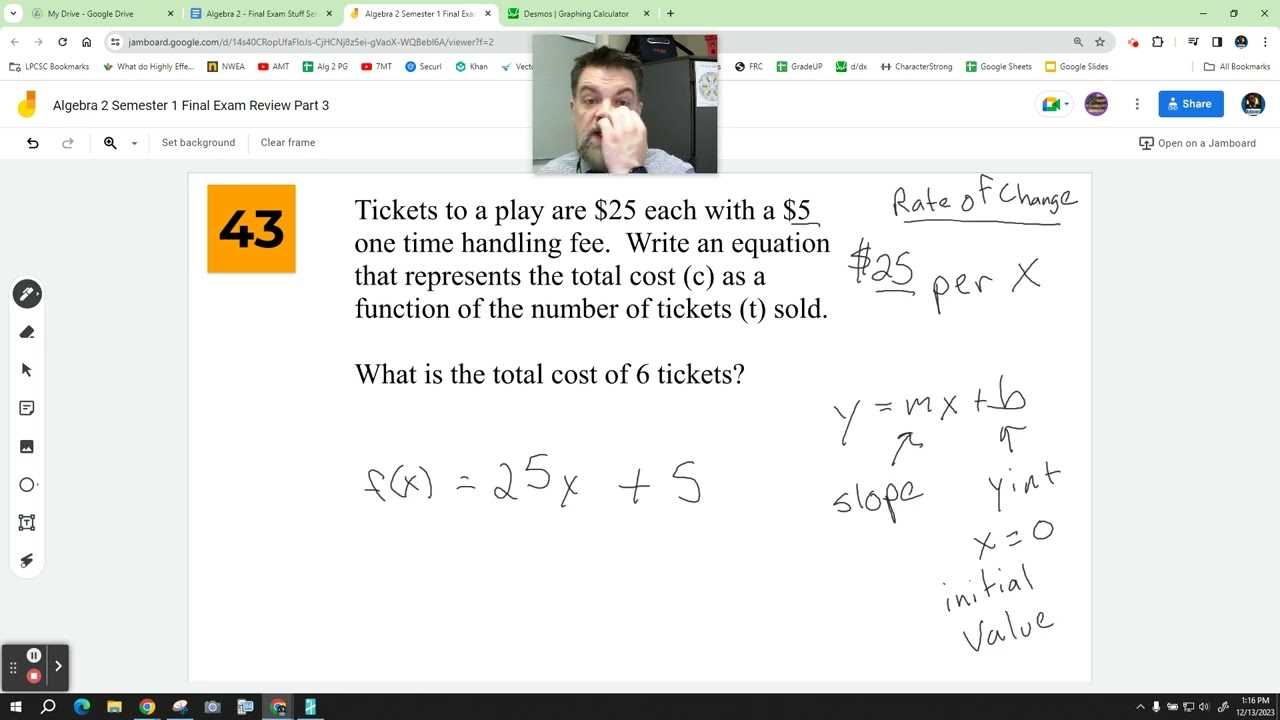
During an assessment, it’s easy to make simple errors that can cost you valuable points. These mistakes are often due to rushed calculations, misinterpretation of questions, or overlooking important details. Recognizing and avoiding common pitfalls will help you perform more accurately and efficiently. By being aware of typical mistakes, you can stay focused and minimize errors throughout the test.
Common Pitfalls
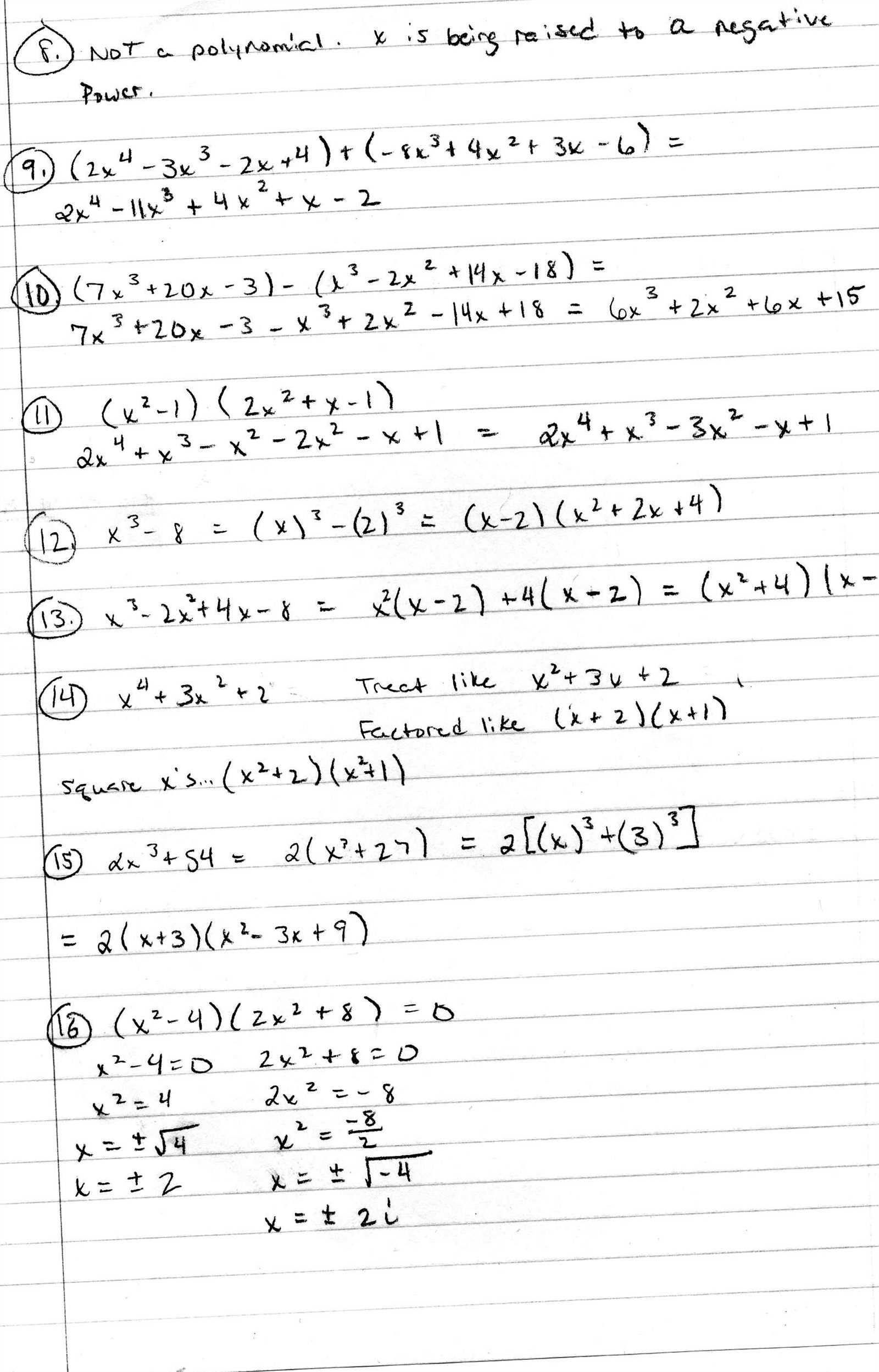
There are several types of mistakes that many students make under pressure. These can range from arithmetic errors to misreading the problem entirely. By understanding the types of mistakes you’re most likely to make, you can avoid them and improve your overall performance.
| Mistake | Impact | How to Avoid |
|---|---|---|
| Skipping Steps | Leads to incomplete or incorrect solutions. | Take time to work through each step methodically. |
| Misreading the Question | Results in solving the wrong problem. | Carefully read the problem twice before starting. |
| Arithmetic Errors | Can cause wrong answers and unnecessary mistakes. | Double-check calculations and use a calculator if allowed. |
| Overcomplicating Simple Problems | Wastes time and causes confusion. | Stay calm, and break problems into simpler parts. |
| Not Reviewing Your Work | Leaves possible errors uncorrected. | Reserve time at the end to check your answers thoroughly. |
Strategies for Avoiding Mistakes

To minimize the likelihood of making these errors, it’s important to develop a systematic approach. Take your time when reading through each problem, and ensure you fully understand what is being asked before starting any calculations. Review your work as you go, and don’t hesitate to revisit questions if you’re unsure of your answer. Staying organized and methodical will help you avoid rushing and making unnecessary mistakes.
By staying mindful of these common mistakes and adopting a careful approach, you’ll increase your chances of achieving a better result.
Effective Study Methods for Algebra
Achieving success in mathematics requires more than just understanding concepts; it involves developing a strategic approach to studying. The right methods can make a significant difference in how well you grasp challenging material and retain information. By adopting effective study strategies, you can improve your performance and approach problems with greater confidence.
| Study Method | Description | Benefits |
|---|---|---|
| Practice Regularly | Consistent problem-solving helps reinforce key concepts. | Increases familiarity with different problem types and improves speed. |
| Break Problems into Steps | Divide complex problems into smaller, more manageable parts. | Reduces overwhelm and helps identify areas that need more attention. |
| Use Flashcards | Create flashcards to test important formulas and concepts. | Improves memory retention and allows for quick review sessions. |
| Work with Study Groups | Collaborate with peers to discuss and solve problems together. | Provides multiple perspectives and can clarify difficult concepts. |
| Seek Help When Needed | Don’t hesitate to ask for clarification from teachers or tutors. | Helps address misunderstandings early and prevents confusion later. |
By utilizing these methods, you will improve not only your understanding of the material but also your ability to apply what you’ve learned. Combining regular practice, strategic review, and collaboration can lead to greater mastery and better results in any mathematical challenge.
Utilizing Practice Tests
One of the most effective ways to prepare for any assessment is to regularly practice with mock tests. These practice sessions allow you to simulate the actual environment, helping you familiarize yourself with the format, time constraints, and types of problems you may encounter. By incorporating practice tests into your study routine, you can identify areas of strength and weaknesses, making your preparation more focused and efficient.
When using practice tests, it’s essential to treat them as real tests. Set aside specific time to complete each one, stick to the time limits, and avoid distractions. This will help you develop the skills needed to manage your time effectively during the real assessment. After completing a practice test, always review your mistakes and ensure that you understand the solutions. This process of self-assessment and reflection is key to improving performance.
By utilizing practice tests regularly, you’ll not only gain more confidence but also improve your ability to approach problems logically and efficiently, increasing your chances of success when it matters most.
How to Handle Test Anxiety

Feeling nervous or anxious before a major assessment is a common experience for many students. However, managing this anxiety is crucial for performing at your best. When faced with pressure, it’s easy to become overwhelmed, but with the right techniques, you can stay calm and focused. Here are some strategies to help reduce stress and improve your performance during any challenging situation.
- Practice Relaxation Techniques: Deep breathing, meditation, and mindfulness exercises can help calm your mind and reduce anxiety.
- Get Enough Sleep: Proper rest is essential for cognitive function and focus. A well-rested mind performs better under pressure.
- Stay Organized: Preparation is key. When you know you’ve studied well, it can help build confidence and reduce unnecessary worry.
- Positive Visualization: Imagine yourself succeeding and tackling problems with confidence. Positive thinking can create a more productive mindset.
- Break the Task Into Manageable Chunks: Avoid feeling overwhelmed by focusing on one problem at a time instead of thinking about the whole assessment.
Implementing these techniques before and during the test can help you manage your anxiety effectively. With practice and the right mindset, you’ll be able to approach challenges calmly and confidently, increasing your chances of success.
Final Exam Success Strategies
Approaching a major assessment requires careful planning, focused preparation, and mental clarity. Success on such a test isn’t just about what you know, but how you approach the challenges. By adopting effective strategies, you can optimize your performance and approach each problem with confidence. Below are key methods that can help you excel on test day.
Preparation Techniques
- Create a Study Schedule: Plan your study sessions in advance to ensure you cover all topics. Break your schedule into manageable chunks to avoid cramming.
- Review Key Concepts: Focus on understanding core ideas and formulas, and spend extra time on areas where you feel less confident.
- Practice with Sample Problems: Doing practice problems allows you to apply your knowledge and build familiarity with the types of questions you may encounter.
- Stay Consistent: Consistent study sessions are more effective than last-minute study marathons. Stick to your schedule for steady progress.
Test Day Strategies
- Arrive Early and Prepared: Ensure you have all necessary materials (pens, pencils, calculator, etc.) and arrive at the testing site early to avoid feeling rushed.
- Manage Your Time Effectively: Start by skimming through the entire test, and allocate your time based on the difficulty and length of each section.
- Read Instructions Carefully: Make sure you understand each question before answering. Rushed mistakes can cost you valuable points.
- Stay Calm and Confident: If you encounter a difficult question, move on and come back to it later. Stay positive and trust in your preparation.
By implementing these strategies in your study routine and on test day, you’ll be better equipped to handle challenges and perform to the best of your ability. With the right mindset and preparation, you can achieve success on any assessment.