In this section, we will explore how to effectively handle mathematical operations that involve splitting numbers and simplifying expressions. Understanding these techniques is crucial for solving complex problems and improving computational skills.
By breaking down larger calculations into smaller, more manageable steps, learners can gain confidence and accuracy in tackling even the most difficult tasks. This approach is not only practical but also enhances overall problem-solving abilities.
Through clear examples and practice exercises, you will learn how to apply these strategies in various contexts. Mastery of these concepts opens the door to solving a wide range of mathematical challenges with ease.
Understanding the Distributive Property in Division

In mathematical calculations, breaking down a complex expression into simpler parts can make it easier to solve. This approach allows for a clearer understanding of how numbers interact and helps to streamline the solving process. By applying specific techniques, large problems can be split into smaller, more manageable components.
How It Works
When performing operations involving larger numbers, one can separate parts of the numbers to simplify the process. This technique helps avoid complicated steps by distributing parts of a number across another, making it easier to compute each piece individually. Once each section is solved, the results are combined to reach the final answer.
Real-World Examples
In real-life applications, this approach can be used in various situations such as budgeting, measuring, or distributing resources. By dividing tasks or quantities into smaller portions, problems that seem overwhelming can become much easier to tackle and understand.
Key Concepts of Division and Distribution
In mathematics, understanding how to break down complex calculations into smaller, simpler steps is essential for problem-solving. These techniques not only make large problems more manageable but also allow for a deeper understanding of the relationships between numbers. By separating a calculation into parts, it becomes easier to handle and solve.
One important concept is the ability to split numbers into smaller components. This allows for more straightforward operations and reduces the complexity of larger expressions. The ability to apply this principle correctly is vital for achieving accurate results in both basic and advanced tasks.
How Division Affects Mathematical Equations
When performing calculations, breaking a number into smaller, more manageable parts can significantly influence how an equation is solved. This process often simplifies otherwise complex problems, leading to quicker and more accurate results. Understanding how this operation alters expressions is key to mastering mathematical problem-solving.
Impact on Balance of Equations
In any equation, maintaining balance is crucial. By applying this operation, numbers are distributed evenly, which helps to preserve the equality of both sides. This ensures that the equation remains valid and that the solution process stays straightforward, without unnecessary complications.
Transforming Larger Problems into Simpler Forms
Complex problems that initially seem overwhelming can be transformed into simpler ones by strategically separating terms. This method reduces the difficulty of calculating large sums and allows for a clearer path to solving the equation, making it easier to understand how numbers relate to each other.
Breaking Down the Distributive Property
In mathematical calculations, breaking a number or expression into smaller, more manageable sections can make complex problems easier to solve. This method allows you to handle large expressions by simplifying them into parts that are easier to compute. Understanding how to split and combine different components is crucial for achieving accurate results.
Step-by-Step Process
To effectively break down an expression, you must identify parts that can be grouped or separated. Once the sections are identified, the operation can be applied to each part individually. Afterward, the results are combined to get the final answer, making the entire process more efficient and less overwhelming.
Why It Works
This method works because it maintains the integrity of the original equation while simplifying the steps. By applying the operation to smaller components, you avoid complex calculations and reduce the chance of making errors. Each smaller part can be calculated independently, allowing you to focus on one piece at a time.
Steps to Solve Division Problems Using Distribution
When tackling complex mathematical problems, breaking them down into simpler steps is crucial for accuracy and efficiency. By applying a strategic approach, large expressions can be separated into smaller components, making it easier to solve each part individually. Follow these steps to solve problems using this technique:
- Identify the terms – Look for the numbers or expressions that need to be split or distributed. Recognize parts that can be handled separately.
- Separate the components – Break the terms into smaller, more manageable groups, focusing on the most straightforward sections first.
- Apply the operation – Perform the necessary calculation for each separated part individually, ensuring no steps are skipped.
- Combine the results – Once each section is calculated, combine the results to arrive at the final solution.
- Double-check your work – Review each step to confirm that all parts have been correctly calculated and combined.
By following these steps, you’ll be able to simplify complicated problems and solve them with confidence, leading to faster and more accurate results.
Common Mistakes in Applying the Distributive Property
When working through mathematical problems, it’s easy to make errors in how terms are handled. While breaking down an expression can simplify the calculation, improper application of this technique can lead to incorrect results. Understanding these common mistakes helps in avoiding pitfalls and ensures more accurate solutions.
Misidentifying Terms: One frequent mistake occurs when terms are not properly separated. If a part of the expression is overlooked or misgrouped, it can distort the final result. Always ensure that all components of the equation are considered before proceeding.
Incorrectly Combining Results: After applying the operation to each part, some individuals mistakenly add or multiply incorrectly. It’s essential to keep track of each intermediate step and combine the results in the proper order to avoid errors.
Overcomplicating the Process: Sometimes, trying to apply the method to overly complex expressions leads to confusion. If the initial breakdown is too complicated, it’s easy to miss key details. Keep the process as simple as possible to stay focused on the primary goal.
By being aware of these mistakes, you can improve your accuracy and become more confident when working through similar problems.
Practical Examples of Division with Distribution
Understanding how to break down large problems into smaller, simpler parts can be extremely helpful in solving complex equations. By applying this technique, you can make calculations easier to handle and more accurate. Below are a few practical examples to demonstrate how this approach works in real-world scenarios:
Example 1: Distributing Large Numbers
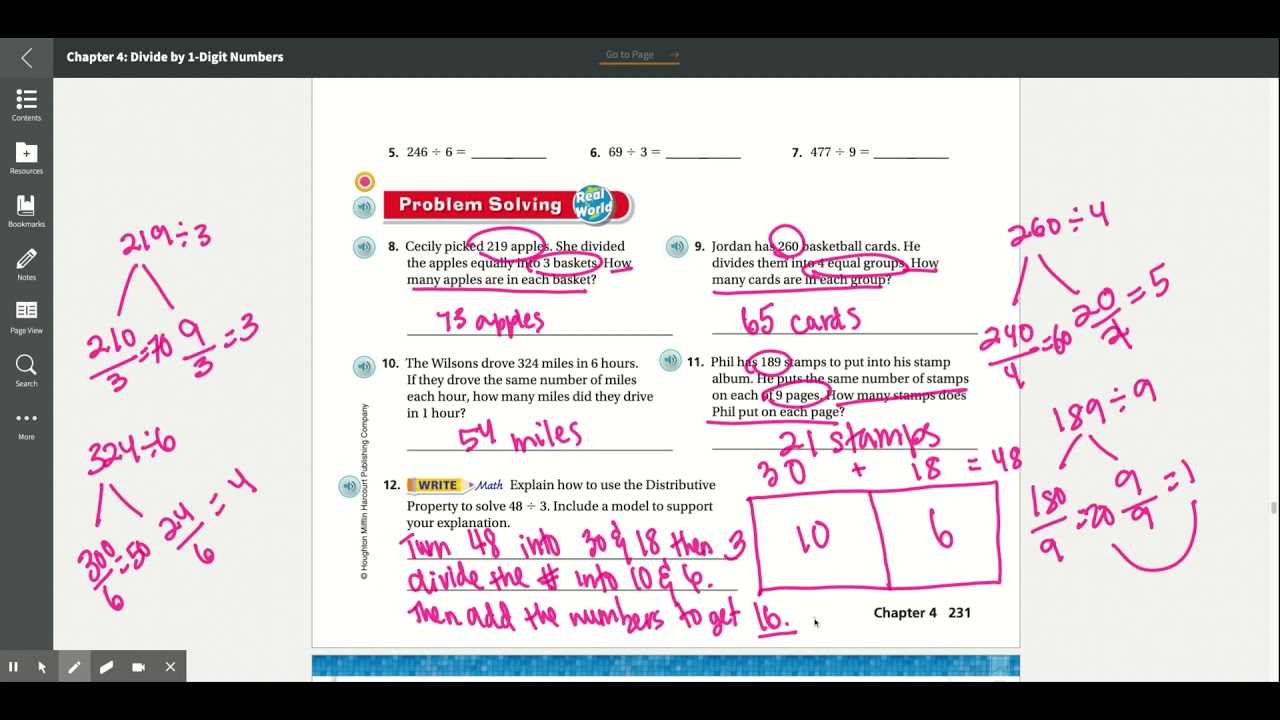
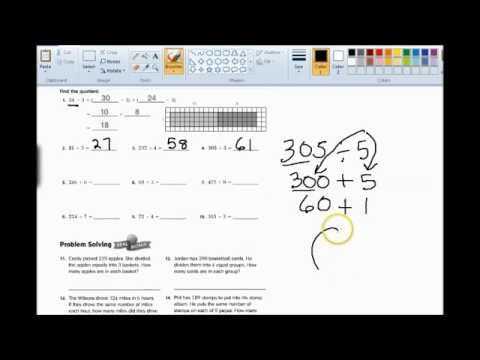
Imagine you need to calculate 72 ÷ 6. Instead of working with the entire number at once, you can break 72 into smaller, easier parts:
- First, break 72 into 60 + 12.
- Next, divide each part by 6: 60 ÷ 6 = 10 and 12 ÷ 6 = 2.
- Finally, add the results: 10 + 2 = 12.
The final result is 12, and this method helps simplify the calculation process.
Example 2: Splitting Larger Multiplicative Terms
Consider a more complex problem such as 56 ÷ 7 in which you break down the components of the larger number:
- Break 56 into 49 + 7.
- Now, divide each section by 7: 49 ÷ 7 = 7 and 7 ÷ 7 = 1.
- Finally, combine the results: 7 + 1 = 8.
This method simplifies the equation and makes it much easier to solve.
Example 3: Using Distribution in Real-World Situations

In everyday situations, this approach is also useful. For instance, if you are sharing 120 apples among 4 people:
- Break 120 into 100 + 20.
- Divide each section by 4: 100 ÷ 4 = 25 and 20 ÷ 4 = 5.
- Combine the results: 25 + 5 = 30.
Each person gets 30 apples, showing how this technique can be applied in daily scenarios like dividing resources.
By practicing these examples, you can become more confident in solving mathematical problems using this effective approach. Whether working with numbers in a classroom setting or solving real-world challenges, this method makes complex tasks more manageable.
Exploring the Relationship Between Division and Multiplication
Mathematical operations often work hand in hand, with one helping to simplify or reverse the other. Understanding the connection between multiplying and splitting numbers can provide a deeper insight into how mathematical problems are structured. By recognizing how these operations complement each other, it becomes easier to solve equations and manipulate expressions effectively.
How Multiplication Reverses the Process
Multiplication is essentially the inverse of splitting numbers. When you divide, you are distributing a number into smaller groups, while multiplying involves combining those groups. For example, if you know that 4 × 5 = 20, you can reverse the process by dividing 20 by 5 to return to the original number 4. This relationship helps in solving both multiplication and splitting problems.
Using Multiplication to Check Division
Another key aspect of the relationship is using multiplication to verify division results. If you have a division problem, you can check your answer by multiplying the result by the divisor. For example, if 48 ÷ 8 = 6, you can multiply 6 × 8 = 48 to confirm the correctness of your division.
Understanding this interconnectedness between multiplying and splitting numbers allows for a more fluid approach to solving problems, enhancing both speed and accuracy in mathematical operations.
How to Simplify Division Problems Efficiently
When facing complex mathematical tasks, breaking them down into simpler steps can significantly speed up the process. Streamlining the problem-solving approach allows for quicker calculations without sacrificing accuracy. By using basic strategies to handle large numbers or challenging equations, you can easily reach the correct answer with minimal effort.
Breaking Numbers into Smaller Parts
One of the most effective methods for simplifying problems is to break larger numbers into smaller, more manageable components. For instance, if you need to solve 72 ÷ 6, split 72 into 60 + 12. Then, handle each part individually by solving 60 ÷ 6 = 10 and 12 ÷ 6 = 2, then combine the results: 10 + 2 = 12.
Look for Common Factors
Another useful approach is to identify any common factors between the numbers involved. If both numbers share a common factor, dividing by that factor first can simplify the calculation. For example, for 48 ÷ 12, you can recognize that both 48 and 12 are divisible by 12. This allows you to directly divide without needing to perform complex steps.
By employing these strategies, you can quickly solve even the most challenging problems without becoming overwhelmed, making your approach both efficient and effective.
Why the Distributive Property is Essential
Understanding how to break down larger problems into smaller, more manageable parts is crucial for solving many types of mathematical equations. This concept allows for more efficient calculations and is a foundational skill in both basic arithmetic and more advanced topics. The ability to apply this method simplifies complex problems, making them easier to approach and solve.
Advantages of Using This Concept
- Simplifies Complex Calculations: Breaking down large numbers or expressions into simpler components makes it easier to handle and solve equations.
- Improves Accuracy: By dividing problems into smaller pieces, it’s easier to identify mistakes early and correct them.
- Enhances Problem-Solving Speed: This method helps solve equations faster by reducing the need for lengthy or complicated steps.
Real-World Applications
- Everyday Math: Whether you’re budgeting or calculating distances, this skill can be used in various everyday tasks.
- Advanced Studies: In algebra, calculus, and other higher-level math courses, this skill is essential for simplifying equations and solving for unknowns.
Mastering this concept is not only important for academic success but also for practical problem-solving in daily life. It creates a strong foundation for tackling more challenging math tasks.
Real-Life Applications of the Distributive Property
The ability to break down complex problems into simpler parts is a valuable skill that extends beyond mathematics. In everyday life, this concept is frequently used in budgeting, shopping, and even in work-related tasks. By applying this technique, individuals can simplify calculations and make more informed decisions quickly and efficiently.
Budgeting and Finance
When managing finances, this method can help split larger expenses into smaller, more manageable categories. For example, if you have a monthly budget for groceries and household items, you can break down the total amount spent into smaller, easier-to-understand portions. If a grocery bill is $120 and you want to allocate 30% of the total for snacks and 70% for meals, you can quickly calculate each portion by applying this technique, resulting in $36 for snacks and $84 for meals.
Shopping Discounts and Offers
Another common application is in understanding discounts. When sales offer a percentage off an item, this method allows you to calculate the discount and final price efficiently. For example, if a jacket costs $80 and there’s a 25% off promotion, instead of calculating 25% of the full price directly, you can break down the price: calculate 20% first ($16), then 5% of the original price ($4), adding both to get the total discount of $20. This leaves you with a final price of $60.
These practical applications show how breaking down numbers into smaller parts can save time and reduce the complexity of everyday decisions, making tasks more manageable and easier to understand.
Visualizing Division Using the Distributive Method
One of the most effective ways to understand complex calculations is by visualizing how numbers are broken down into smaller parts. This approach not only simplifies mathematical problems but also provides a clearer picture of how values relate to one another. By representing larger numbers as sums or differences, it becomes easier to see how each part contributes to the final result. This method of visualizing allows for a more intuitive understanding of the process involved in solving problems.
Breaking Numbers into Manageable Parts
Imagine you need to calculate 48 ÷ 6. Instead of performing the operation directly, you can split 48 into smaller parts, such as 30 + 18, which are easier to work with. From there, you can divide each part by 6 individually: 30 ÷ 6 = 5 and 18 ÷ 6 = 3. Finally, you combine the results: 5 + 3 = 8. This method visually illustrates how the total is distributed across different values, providing a more accessible solution.
Applying Visualization in Word Problems
In real-life scenarios, this technique can be applied to various types of problems, such as sharing resources or distributing items. For example, if you have 60 apples and need to divide them equally among 5 baskets, you can break down 60 as 50 + 10 and divide each part by 5: 50 ÷ 5 = 10 and 10 ÷ 5 = 2. So, each basket gets 12 apples, making the calculation easier to visualize and understand.
By visualizing problems in this way, it becomes much easier to grasp the relationship between numbers and how they interact in more complex calculations. This method not only aids in better comprehension but also builds a stronger foundation for approaching future mathematical challenges.
Understanding the Formula for Division with Distribution
When solving complex mathematical operations, breaking down numbers into smaller, more manageable parts can simplify the process. By applying a specific formula, you can distribute values across different components to make calculations easier. This formula is particularly helpful in solving problems that involve large numbers or require more detailed analysis.
The concept is based on dividing a number by smaller segments and then adding the results. The general approach works by splitting a larger number into smaller addends or subcomponents, applying the operation to each part, and then combining the individual results.
| Original Problem | Split Components | Result for Each | Final Result |
|---|---|---|---|
| 56 ÷ 4 | 40 + 16 | 40 ÷ 4 = 10 16 ÷ 4 = 4 |
10 + 4 = 14 |
| 84 ÷ 7 | 70 + 14 | 70 ÷ 7 = 10 14 ÷ 7 = 2 |
10 + 2 = 12 |
By breaking down each number into its components, you can quickly determine the result through straightforward calculations. This method reduces the complexity of larger problems and provides a more approachable solution to what might initially seem like a difficult task.
Understanding this formula can not only help in solving equations but also improve your ability to work through larger problems by focusing on the parts that make up the whole. It is a versatile technique that can be applied to a variety of scenarios, whether in basic arithmetic or more advanced problem-solving contexts.
Why Division Can Be Challenging for Students
Many students struggle with certain mathematical operations due to their inherent complexity and the need for multiple steps to arrive at a solution. For some, understanding the logic behind these steps can be a difficult hurdle. In particular, one of the more challenging areas involves breaking down larger numbers into smaller, manageable parts while maintaining accuracy. This complexity can make it harder for learners to grasp the core concepts, leading to confusion and frustration.
Difficulty with Mental Math and Estimation
One major difficulty students encounter is the need for quick mental calculations. Unlike addition or subtraction, where numbers can often be combined or reduced directly, this operation often requires estimating how many times a smaller number fits into a larger one. For students who struggle with mental math, this estimation process can be a barrier to success. As they attempt to visualize how the numbers relate to each other, they may feel overwhelmed or uncertain about how to proceed.
Challenges with Complex Problems
As problems grow in complexity, students often face confusion with multi-step processes. Breaking down a single equation into smaller components and managing intermediate results requires a strong foundation in mathematical reasoning. Without proper understanding, it’s easy to make mistakes in carrying over numbers or misapplying certain rules. This can result in incorrect answers and a lack of confidence in tackling more advanced problems.
Additionally, the use of abstract concepts like grouping or reorganizing numbers can make it harder to see the connections between different mathematical ideas. This is especially true for students who have not yet developed a clear mental model for these operations, making it difficult for them to understand how to simplify or restructure equations.
By focusing on building foundational skills and providing more hands-on practice with real-world examples, educators can help students overcome these challenges and feel more confident in their abilities. Understanding the underlying logic and recognizing patterns can transform this area from a challenge into an achievable goal.
Tips for Mastering Division and Distribution Together
Successfully solving problems that combine splitting numbers and expanding expressions requires a solid understanding of how both concepts interact. These techniques can simplify complex calculations and make it easier to work with larger values. The key is to break down steps carefully and apply logical reasoning consistently.
Approach with Smaller Parts
One effective strategy is to first tackle smaller, more manageable parts of a problem. Instead of working with an entire expression at once, try to simplify it by isolating sections that are easier to handle. By focusing on these smaller units, you can apply each method step by step, making it simpler to understand the overall process.
Understand How Values Interact
Another crucial tip is recognizing how values within the expression relate to each other. It’s important to consider how numbers combine and separate through different operations. Mastering these connections allows for faster problem-solving and fewer errors in calculations.
| Step | Action | Benefit |
|---|---|---|
| 1 | Break down larger numbers into smaller units | Helps simplify complex problems into easier parts |
| 2 | Apply one technique at a time | Reduces confusion and increases accuracy |
| 3 | Practice with a variety of examples | Enhances familiarity with different types of problems |
By following these tips, anyone can gain a better understanding of how to efficiently handle tasks that involve both splitting values and expanding expressions. With practice, solving these types of problems becomes much easier.