In this section, we explore critical topics that are essential for mastering the art of analyzing sequential data. The ability to understand trends, patterns, and fluctuations over time is fundamental in a wide range of subjects, from economics to environmental science. This knowledge is key for interpreting data accurately and making informed decisions based on past performance.
Analyzing data over intervals presents unique challenges that require a deep understanding of mathematical models and statistical tools. The key to success lies in recognizing recurring patterns and effectively forecasting future behavior. With the right approach, these concepts can be applied to a variety of practical situations, helping solve complex problems.
By focusing on core methods, model selection, and common issues, this guide provides a clear pathway for building a strong foundation. Whether preparing for an assessment or enhancing your practical skills, mastering these techniques will allow you to tackle advanced topics with confidence and precision.
Time Series Exam Questions and Answers

Understanding how to approach problems related to sequential data analysis is essential for success in assessments. This section provides an overview of the most common tasks and challenges faced when analyzing patterns and making predictions based on historical data. By breaking down key concepts and techniques, you can improve your ability to solve complex problems with confidence.
Key Topics to Focus On
When preparing for assessments, it is crucial to focus on several core topics that form the foundation of sequential data analysis. These include understanding trends, recognizing seasonality, identifying autocorrelation, and learning how to forecast future outcomes. Mastering these elements ensures a strong understanding of the material and the ability to approach a wide variety of problems effectively.
Common Mistakes to Avoid
Many students struggle with common pitfalls during their assessments. One frequent challenge is misinterpreting data due to the lack of proper analysis techniques. It’s important to avoid errors like overlooking outliers or failing to account for changes in patterns. Practicing with different types of data will help you recognize potential mistakes before they impact your performance.
Understanding Key Concepts in Time Series
Grasping the fundamental principles of analyzing sequential data is crucial for interpreting patterns, predicting future values, and making data-driven decisions. This section focuses on the essential building blocks necessary for understanding how historical data can be used to identify trends, seasonality, and irregular behaviors. Mastery of these concepts sets the stage for more advanced analytical techniques.
Important Characteristics of Sequential Data
Sequential data has specific characteristics that differentiate it from other types of datasets. Identifying and understanding these features helps in making accurate predictions and effective analyses. The most critical aspects include:
| Feature | Description |
|---|---|
| Trend | Long-term movement in data over time, either increasing or decreasing. |
| Seasonality | Regular, repeating patterns at consistent intervals. |
| Irregularity | Unpredictable fluctuations or random events that disrupt the regular pattern. |
| Noise | Random variations that do not follow a discernible pattern. |
How to Identify Key Patterns

Identifying recurring trends and patterns in sequential data is a fundamental skill for any analyst. By using various visualization tools and statistical tests, you can pinpoint where the data follows specific behaviors over time. This includes recognizing consistent fluctuations (seasonality) and long-term shifts (trends). Mastering this process enables more accurate forecasting and effective decision-making based on historical data.
Common Time Series Models to Know
Understanding the different models used to analyze sequential data is key to effectively interpreting patterns and forecasting future values. Each model has its own strengths and is suited for specific types of data behavior. Knowing which models to apply in various situations allows analysts to draw meaningful insights and make data-driven decisions with confidence.
Among the most commonly used models are autoregressive (AR), moving average (MA), and their combinations, such as the ARMA model. These models focus on understanding relationships within the data itself, using past values to predict future outcomes. More complex approaches, like ARIMA and seasonal decomposition methods, are also essential tools for handling data with seasonality or irregular fluctuations.
How to Approach Time Series Questions
Approaching problems related to sequential data requires a structured method to ensure accuracy and efficiency. The key to success lies in breaking down the task into manageable steps, from understanding the problem’s context to selecting the right analytical techniques. By following a logical approach, you can tackle even the most complex issues with confidence.
The first step is to thoroughly examine the given data. Identify any trends, seasonal patterns, or irregular behaviors that may affect the results. Once you have a clear understanding of the data’s structure, the next step is to choose the appropriate model or technique for analysis. Always consider the nature of the data before deciding on methods for prediction or forecasting.
Essential Formulas for Time Series Analysis
Understanding key formulas is crucial for effectively analyzing sequential data and making accurate predictions. These formulas help quantify trends, measure relationships between data points, and evaluate the performance of different models. By mastering these mathematical tools, you can gain deeper insights into data behavior and improve your forecasting accuracy.
Basic Statistical Formulas
Several fundamental formulas are essential for analyzing sequential data. These include measures of central tendency, variability, and correlation. Below are some important calculations:
- Mean (Average): μ = (Σx) / n – used to determine the average value of a dataset.
- Variance: σ² = (Σ(x – μ)²) / n – measures the spread or variability of the data.
- Standard Deviation: σ = √σ² – gives the square root of variance, providing an easier interpretation of data spread.
- Covariance: cov(X,Y) = Σ[(Xi – μX) * (Yi – μY)] / n – measures the relationship between two variables.
Key Forecasting Formulas
For accurate forecasting, certain equations are indispensable. These formulas help predict future values based on past observations:
- Autoregressive Model (AR): X(t) = c + φ1 * X(t-1) + φ2 * X(t-2) + … + ε(t) – uses past data points to predict future values.
- Moving Average (MA): X(t) = (1/n) * ΣY(t-i) – smoothens data by averaging a set number of past values.
- ARIMA Model: ARIMA(p, d, q) – a combination of autoregressive, differencing, and moving average techniques for complex datasets.
Interpreting Trends in Time Series Data
Recognizing patterns and long-term movements within sequential data is crucial for making informed decisions and predictions. Trends reflect consistent increases or decreases over a period, providing insights into underlying behaviors that may not be immediately apparent in short-term fluctuations. Analyzing these trends allows analysts to forecast future outcomes and understand the driving factors behind data changes.
Types of Trends to Identify
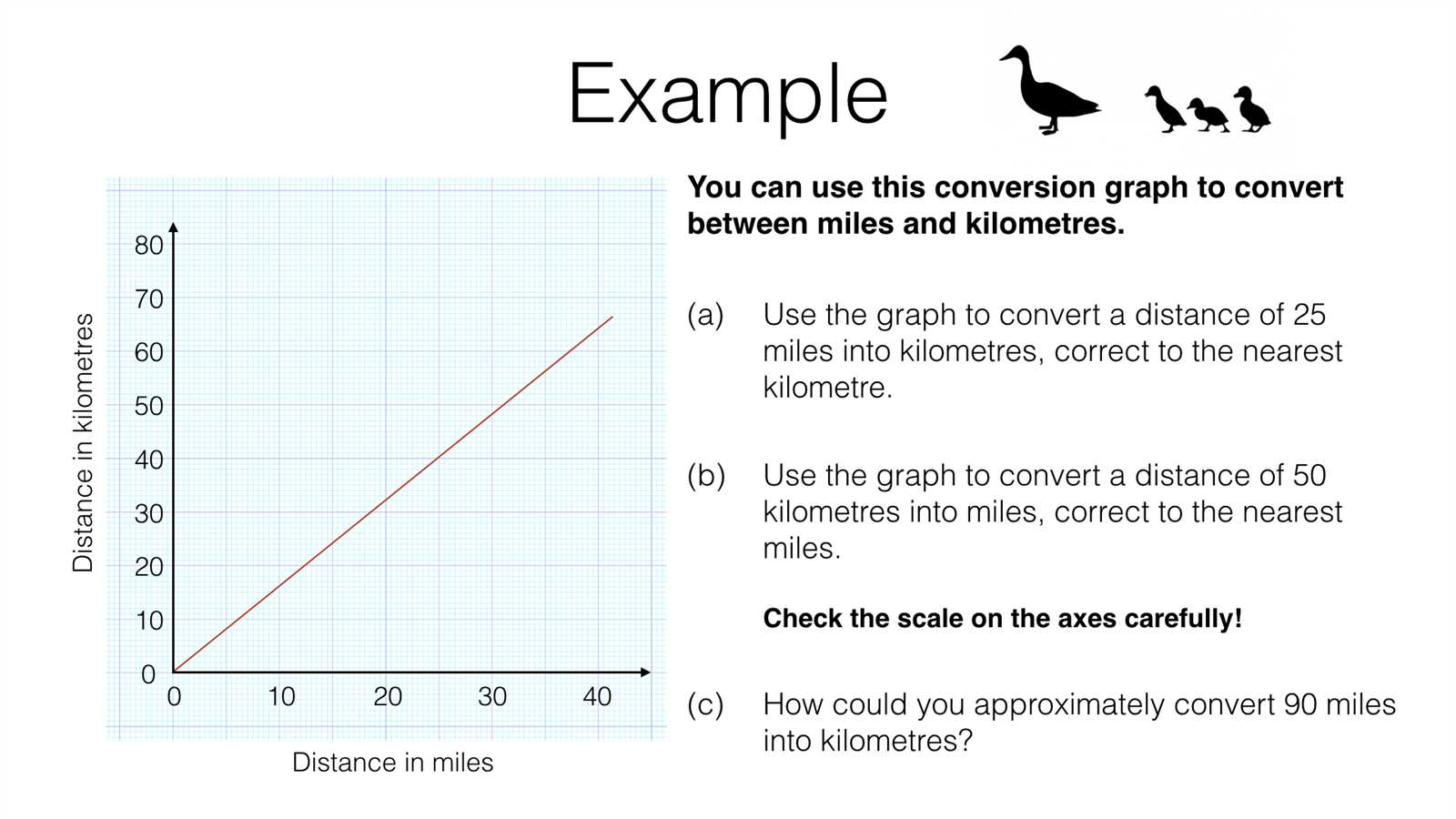
When examining data, it is essential to distinguish between different types of trends. Here are some key categories:
- Linear Trend: A constant increase or decrease in values over time, often represented by a straight line.
- Exponential Trend: A rapid rise or fall, where changes occur at an accelerating rate, often seen in growth patterns.
- Logarithmic Trend: A slower growth or decay, typically seen in processes that slow down as they reach a limit.
- Constant Trend: Data that remains stable or shows little fluctuation over time.
Methods for Analyzing Trends
Various techniques are available to identify and quantify trends. Common methods include:
- Moving Averages: A smoothing technique used to highlight underlying trends by averaging data over specific intervals.
- Linear Regression: A statistical method for fitting a straight line to the data, helping identify a linear trend.
- Exponential Smoothing: A technique that gives more weight to recent observations, useful for detecting emerging trends.
- Decomposition: Breaking down data into trend, seasonal, and residual components to analyze long-term movements more clearly.
Seasonality and its Role in Time Series
In sequential data analysis, recurring patterns that repeat over specific intervals play a crucial role in understanding fluctuations and predicting future outcomes. These regular patterns, often linked to time-based factors such as seasons, holidays, or even business cycles, can significantly influence data behavior. Recognizing and modeling these cycles helps improve the accuracy of forecasts and the interpretation of long-term trends.
Understanding Seasonal Patterns
Seasonality refers to periodic variations that happen at consistent intervals due to external factors. These variations are often predictable, making them crucial for accurate forecasting. Key seasonal factors can include:
- Annual Cycles: Patterns that repeat every year, such as higher sales during the holiday season or temperature changes during different months.
- Quarterly Trends: Fluctuations tied to business quarters, like sales spikes at the end of fiscal periods.
- Monthly Fluctuations: Seasonal behaviors within a specific month, often linked to weather changes or cultural events.
- Weekly Cycles: Changes observed over the course of a week, often influenced by work schedules or consumer habits.
Methods for Identifying and Modeling Seasonality
Various techniques are used to identify and account for seasonal patterns within data. These methods help ensure that models accurately reflect the recurring cycles. Common approaches include:
- Seasonal Decomposition: Breaking down data into trend, seasonal, and residual components to isolate seasonal effects.
- Seasonal Adjustment: Removing seasonal effects to focus on underlying trends and irregularities.
- Fourier Transforms: A mathematical technique used to identify and extract periodic components from data.
- ARIMA with Seasonal Differencing: A modification of the ARIMA model that accounts for seasonal patterns in the data.
Identifying Autocorrelation in Time Series
Autocorrelation measures the relationship between observations in a dataset at different time points. Recognizing patterns in past values that influence future observations is essential for accurate forecasting and model development. When data points are not independent, but instead show dependencies, detecting these correlations becomes a key part of understanding the structure of the data and improving prediction accuracy.
To identify autocorrelation, it’s important to examine the data for repeating patterns or significant correlations over time. If past observations have a systematic influence on future values, this can suggest the presence of autocorrelation. The strength and direction of this correlation can provide valuable insights into how a given variable behaves over different intervals, helping analysts make more informed predictions.
Handling Missing Data in Time Series
Dealing with gaps in data is a critical aspect of sequential analysis. Missing values can distort the accuracy of models and forecasts, leading to unreliable predictions. Whether due to errors in data collection, transmission issues, or incomplete reporting, it’s essential to identify the cause of missing data and apply appropriate techniques for managing these gaps without compromising the integrity of the analysis.
Common Approaches to Handling Missing Data
There are several strategies available for addressing missing values in a dataset. The method chosen will depend on the nature of the data, the amount of missing information, and the impact on overall analysis:
- Deletion: Removing the missing values completely from the dataset, which is suitable when there are very few missing points and the removal does not significantly affect the analysis.
- Imputation: Replacing missing values with estimated ones based on available data. This can be done using techniques such as mean imputation or interpolation methods.
- Forward/Backward Filling: Using the most recent or subsequent available data point to fill the missing value, typically used when data follows a consistent trend or pattern.
- Model-based Methods: Employing statistical models, such as regression or machine learning algorithms, to predict missing values based on relationships in the data.
Impact of Missing Data on Analysis
Handling missing data carefully is crucial to ensure the accuracy of any predictions or insights drawn from the analysis. If missing values are not properly addressed, they can lead to biased results or incorrect assumptions. Thus, it is important to choose the most appropriate technique based on the extent and nature of the missing information to minimize potential errors.
Time Series Forecasting Methods Explained
Predicting future outcomes based on historical data is a crucial skill for making informed decisions across various fields, from economics to marketing. By analyzing past trends and patterns, different forecasting methods can be applied to predict future behavior with a certain degree of accuracy. Each method has its strengths, depending on the characteristics of the data and the forecast horizon.
Popular Forecasting Techniques
Several approaches exist to project future values based on historical data. Here are some of the most widely used methods:
- Moving Averages: A simple yet effective method that smooths past data to forecast future trends. It helps to reduce short-term fluctuations and highlight longer-term trends.
- Exponential Smoothing: This method applies decreasing weights to past observations, with more recent data being given higher importance. It’s effective when there is a strong trend or seasonality.
- ARIMA (AutoRegressive Integrated Moving Average): A more advanced technique that combines autoregressive, moving average, and differencing components to model time-dependent relationships in the data.
- Machine Learning Models: Techniques like Random Forests, Support Vector Machines, or Neural Networks that can capture complex, non-linear relationships in data for more accurate forecasts.
Choosing the Right Method

Selecting the appropriate forecasting method depends on factors such as data characteristics, the presence of trends or seasonal patterns, and the desired forecast horizon. For instance, if the data is highly volatile with minimal trend or seasonality, moving averages might be sufficient. On the other hand, if data exhibits strong seasonal fluctuations, more sophisticated methods like exponential smoothing or ARIMA may be required for better accuracy.
Stationarity in Time Series Analysis
For effective forecasting and modeling, it is essential to understand whether a dataset’s statistical properties remain constant over time. If these properties fluctuate or change with different time intervals, the data may not be suitable for certain types of predictive models. Identifying and addressing this issue is crucial, as many advanced models assume data stability over time.
Why Stationarity Matters
Stationary data simplifies analysis by ensuring that the underlying patterns remain consistent. Models like ARIMA rely on this consistency, as they work best when the data’s mean, variance, and autocorrelation do not change. Without stationarity, predictions may become inaccurate, and forecasting errors could increase over time.
How to Check for Stationarity
There are several methods to test for stationarity in a dataset. One of the most commonly used approaches is the Augmented Dickey-Fuller (ADF) test, which examines whether a unit root is present, indicating non-stationarity. Another approach is to visually inspect the data through plots, such as autocorrelation functions, to detect irregular patterns in the data.
In cases where data is not stationary, techniques like differencing, transformation, or detrending can be applied to stabilize the dataset and make it more suitable for modeling and forecasting.
Model Selection for Time Series Problems
Choosing the right model is a critical step in analyzing sequential data, as it directly influences the quality and accuracy of predictions. With various modeling techniques available, each suited to different types of data patterns, it is important to carefully evaluate the characteristics of the data before selecting an appropriate model. The choice of model impacts how well future trends are captured and forecasted.
In general, the model selection process involves analyzing data for specific patterns, such as trends, seasonality, and irregular fluctuations. Once the data characteristics are understood, the selection process can begin with a focus on the model that best fits the observed patterns.
Factors Influencing Model Choice

When selecting a model for a given problem, several factors should be taken into account:
| Factor | Considerations |
|---|---|
| Data Structure | Does the data show clear trends, cycles, or seasonality? Is it stationary? |
| Forecast Horizon | Are you forecasting short-term or long-term outcomes? Some models are better suited for specific time frames. |
| Data Frequency | How often is data collected? High-frequency data may require different approaches compared to low-frequency data. |
| Model Complexity | Is the model simple and easy to interpret, or does it require advanced techniques like machine learning? |
| Data Availability | Do you have enough data for training and validation? Some models require a larger dataset for reliable forecasts. |
Considering these factors will help narrow down the most appropriate model for any given problem. For example, simpler models like moving averages or exponential smoothing might be more effective for data with minimal seasonal effects, while more advanced models like ARIMA or machine learning approaches could be better suited for capturing complex patterns in large datasets.
Common Pitfalls in Time Series Exams

When dealing with assessments that focus on analyzing sequential data, it is easy to make mistakes that can lead to inaccurate interpretations or misapplications of methods. Many individuals, particularly those new to the subject, may overlook critical steps or misapply techniques that are essential for reliable results. Awareness of common mistakes can help prevent errors and ensure a more effective approach during these assessments.
Overlooking Stationarity
One of the most common mistakes is failing to check for stationarity before applying certain models. Without ensuring that the data is stationary, many forecasting techniques can produce misleading or unreliable results. Often, students assume that all data is suitable for direct analysis without transforming it first. Differencing, log transformations, or other methods may be necessary to stabilize the data before further analysis.
Ignoring Model Assumptions
Each modeling technique comes with its own set of assumptions, and ignoring these can lead to inaccurate forecasts. For example, methods like ARIMA require that the data should have certain properties, such as a constant mean and variance. If these assumptions are not met, the model’s performance could degrade. Being mindful of these requirements is crucial for selecting the right approach and achieving meaningful results.
Additionally, relying on complex models without fully understanding their intricacies can also be a trap. It’s important to evaluate whether a more straightforward approach might suffice before resorting to advanced techniques.
Practical Tips for Time Series Questions
When tackling assessments related to analyzing sequential data, applying a strategic approach can make all the difference. Understanding the key concepts, methods, and pitfalls can significantly enhance your performance. Whether you’re working through a complex dataset or answering theoretical questions, a clear method can guide you toward more accurate results and solutions.
1. Understand the Problem Clearly – Before diving into the analysis, make sure you fully grasp the question at hand. Are you being asked to forecast future values, identify trends, or explain the underlying patterns? Knowing the goal of the problem will help you decide the most appropriate tools and techniques to use.
2. Visualize the Data – Always start by plotting the data. Visualization can provide instant insights into any patterns, trends, or anomalies. It’s much easier to spot seasonality, outliers, or irregularities through a simple graph, which will guide you in the next steps of your analysis.
3. Check for Assumptions – Many models rely on certain assumptions, such as stationarity or normality. Be sure to test for these assumptions before proceeding with any model fitting. If the data doesn’t meet the assumptions, consider applying transformations like differencing or logarithms.
4. Stay Organized – When working on any type of analysis, it’s essential to stay organized. Use clear notation and document each step. Whether you’re solving the problem manually or using software, having a structured approach will help prevent errors and save time during your analysis.
5. Practice Regularly – The more you practice solving problems, the more intuitive the process will become. Work through various examples, and try to understand the rationale behind each solution. This will not only improve your skills but also help you become more comfortable with the different methods and approaches used in the field.
Time Series Analysis with Real-World Data
Analyzing real-world sequential data provides a deeper understanding of the patterns and behaviors that drive many industries. From predicting financial market trends to tracking environmental changes, these practical applications often pose unique challenges due to the complexity and variability of the data. Working with real-world datasets requires careful attention to detail and a solid grasp of analytical techniques to draw meaningful conclusions.
Challenges of Working with Real Data
Unlike clean, synthetic datasets, real-world data often contains noise, missing values, and outliers. These imperfections require additional steps in preprocessing, such as cleaning, handling missing values, or smoothing the data. Additionally, real-world datasets may involve irregular time intervals or other complexities, which must be addressed to ensure the accuracy of any forecasts or insights derived from the analysis.
Practical Applications in Industry
Sequential data analysis is widely used in various industries to make informed decisions and predictions. For example, in retail, businesses analyze sales data to predict demand and optimize inventory management. In healthcare, patient data over time is analyzed to detect patterns in disease progression or treatment effectiveness. Financial analysts use similar methods to assess market trends and forecast stock prices. By applying statistical models to real data, professionals can gain insights that drive strategic decision-making and optimize operations.
Preparing for Time Series Exam Challenges
When preparing for assessments involving sequential data analysis, it’s important to familiarize yourself with both the theoretical concepts and the practical methods used in solving related problems. Success in these challenges requires a solid understanding of various techniques, the ability to interpret results accurately, and the application of critical thinking to complex datasets. Thorough preparation not only ensures that you can solve problems efficiently but also helps you avoid common mistakes that often arise during testing.
Mastering Key Concepts is essential. Focus on understanding the core principles that govern trends, seasonality, and statistical methods used for forecasting. A strong grasp of these concepts will allow you to approach problems confidently, knowing how to select and apply the right techniques. Pay attention to model selection, error analysis, and how to evaluate the accuracy of predictions, as these are often central topics in assessments.
Practicing Problem-Solving by working through past examples or similar exercises can be invaluable. This not only helps to reinforce your knowledge but also improves your ability to recognize patterns and trends in the data. In many cases, solving practice problems will highlight areas where you may need further study or review, ensuring that you’re fully prepared for the challenge.
Simulating Exam Conditions can further enhance your readiness. Take practice tests within a set time frame to improve your ability to manage time effectively. This will also help you stay calm under pressure and focus on answering questions systematically.