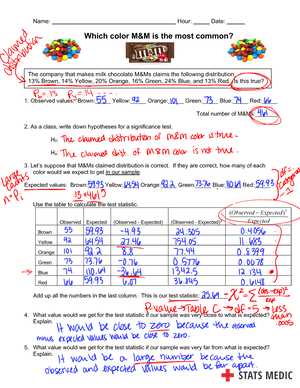
Preparing for an advanced assessment can often be a daunting task, especially when it comes to mastering complex topics and solving intricate problems. This section provides essential insights into the common question formats and solutions, designed to enhance your understanding and performance. With clear explanations and carefully crafted examples, students can gain a deeper grasp of the material.
In-depth solutions are crucial for reinforcing concepts learned during the course. These detailed responses not only clarify the reasoning behind each choice but also help identify common challenges students face. By focusing on specific problem types, you can streamline your preparation process and address areas that need more attention.
Whether you’re aiming for a higher score or seeking to better understand the underlying principles, this guide offers structured assistance. Through a series of step-by-step walkthroughs, we’ll break down each problem, providing clarity on methods, techniques, and necessary calculations.
AP Statistics Test 4B Answer Key
This section provides a comprehensive breakdown of solutions for the fourth examination in the AP course, focusing on the key problem-solving techniques and calculations necessary to succeed. By reviewing the presented solutions, students can gain a better understanding of the various types of questions commonly encountered during the assessment.
Each example is accompanied by detailed explanations, offering insight into the process behind selecting the correct response. From interpreting data to performing critical analysis, these solutions aim to guide students through the reasoning steps, ensuring clarity in both approach and result. This approach helps reinforce the methods used in tackling challenging questions.
By examining the responses closely, students can identify patterns in the types of errors often made, providing an opportunity to refine their problem-solving skills. This section not only clarifies individual queries but also offers valuable strategies for mastering the material in preparation for future assessments.
Overview of Test 4B Content
The fourth assessment in this course covers a wide range of concepts designed to evaluate your understanding and application of advanced methods in data analysis. The questions are structured to test both theoretical knowledge and practical problem-solving skills, focusing on key principles and their real-world applications.
Topics included in this section span across various statistical techniques, such as probability, data interpretation, and hypothesis testing. Each problem requires a careful analysis of provided information, demanding a clear understanding of mathematical relationships and the ability to apply appropriate methods to reach correct conclusions.
This portion of the course also challenges students to synthesize information from multiple areas, ensuring a holistic understanding of the material. Success in this section depends on your ability to approach problems logically, use critical thinking, and draw conclusions based on solid reasoning and calculations.
Key Concepts Tested in 4B
The fourth assessment focuses on a set of core principles that are essential for mastering advanced analytical techniques. These concepts require students to apply both theoretical knowledge and practical skills, ensuring a comprehensive understanding of the subject matter. The focus is on analyzing data, interpreting results, and drawing meaningful conclusions from various scenarios.
Probability and Distribution Analysis
One of the central areas tested in this section involves understanding the likelihood of different outcomes and how data is distributed across various populations. Students are expected to apply probability models and understand the behavior of different distributions, including normal, binomial, and others. The ability to interpret these distributions is crucial for making informed decisions based on data.
Hypothesis Testing and Inference
Another key concept involves drawing inferences from sample data to make predictions or decisions about a larger population. This includes formulating hypotheses, conducting tests, and interpreting p-values. A solid grasp of confidence intervals and error types is necessary for making accurate conclusions from statistical data.
Understanding the Multiple-Choice Section
The multiple-choice segment of this evaluation is designed to assess your ability to quickly and accurately interpret data, apply mathematical techniques, and make decisions based on provided scenarios. These questions are typically structured to test both your conceptual understanding and your ability to apply that knowledge under timed conditions.
Question Structure and Focus Areas
Each question presents a specific problem followed by several potential solutions, with only one being correct. The questions cover a broad range of topics and often require careful analysis to determine the best answer. Key areas include:
- Interpreting data distributions and graphs
- Applying probability models to real-world situations
- Analyzing experimental designs and their outcomes
- Identifying relationships between variables
Tips for Success in the Multiple-Choice Section

To improve your performance in this part of the assessment, consider these strategies:
- Read each question carefully to ensure you understand the scenario being presented before choosing an answer.
- Eliminate clearly incorrect options to increase your chances of selecting the correct one.
- Manage your time effectively by pacing yourself and not spending too long on any single question.
- Double-check your calculations and ensure that they align with the available options.
How to Approach Free-Response Questions
Free-response questions require a more comprehensive and detailed approach compared to multiple-choice items. These questions assess your ability to apply knowledge to solve complex problems, where a clear explanation of your reasoning is just as important as reaching the correct solution. Effectively answering these types of questions involves breaking down the problem, organizing your thoughts, and presenting your solutions step-by-step.
Step-by-Step Problem Solving
When facing a free-response question, it’s important to follow a structured approach:
- Read the question carefully: Ensure you understand what is being asked before starting your solution.
- Identify key information: Highlight important data points and any conditions or constraints that are relevant to solving the problem.
- Plan your approach: Organize your steps logically, whether it’s performing calculations, creating visual representations, or writing out explanations.
- Show all work: Document each step of your process clearly, so the logic behind your answer is easy to follow.
Tips for Clarity and Accuracy
To improve the quality of your responses, consider these strategies:
- Be precise: Avoid vague language and ensure your explanations are direct and easy to understand.
- Use appropriate terminology: Incorporate relevant concepts and terminology to demonstrate your understanding.
- Review your work: Always take a moment to double-check your calculations and reasoning before submitting your response.
Common Mistakes in Test 4B
Even the most prepared students can fall into common traps during an evaluation. These mistakes can stem from misinterpreting the problem, overlooking key details, or rushing through calculations. Identifying these errors in advance can help you avoid them and improve your performance. Below are some of the most frequently observed pitfalls in the fourth assessment.
Misunderstanding the Problem
One of the most common errors is failing to fully grasp what the question is asking. Often, students focus too much on familiar terms or formulas, neglecting to carefully read through the entire scenario. This can lead to applying the wrong method or misinterpreting the data.
- Tip: Take time to read the question multiple times, highlighting key information and identifying exactly what is being asked.
Calculation Errors
Another frequent mistake is making simple mathematical errors, such as miscalculating a mean, misunderstanding how to apply a formula, or using the wrong units. These small errors can add up quickly, especially when multiple steps are involved in solving the problem.
- Tip: Double-check each calculation to ensure accuracy. If possible, use a calculator to verify your work.
- Tip: Keep track of your units and conversions to avoid errors in the final answer.
Rushing Through Explanations
While it’s essential to focus on the technical aspects of the problems, students often neglect to clearly explain their reasoning. Free-response sections require not only the right answer but also a logical, step-by-step explanation. Failing to articulate the process can result in losing points, even if the answer is correct.
- Tip: Always take a moment to clearly document each step of your solution, explaining your thought process as you go.
Scoring Breakdown for AP Statistics
The scoring system for the AP evaluation is designed to assess both the accuracy and the depth of your responses. It not only takes into account the correctness of your answers but also the clarity and thoroughness of your explanations. Understanding how each section is weighted can help you prioritize your time and focus on areas that contribute most to your final score.
The overall assessment is divided into two main sections: multiple-choice questions and free-response problems. Each section is scored independently, with different methods used to evaluate performance.
Multiple-Choice Section
This portion consists of a series of questions where you must choose the correct answer from several options. Points are awarded for each correct choice, with no deductions for incorrect answers. Your ability to quickly analyze and interpret data will play a key role in your performance here.
Free-Response Section
In this section, you are required to provide detailed, written responses to a series of problems. Points are awarded based on the completeness of your solutions, the logical progression of your work, and the accuracy of your conclusions. Clear explanations and correct reasoning are just as important as finding the right answers.
Reviewing Key Formulas for 4B
Having a strong grasp of essential formulas is critical when tackling problems in this assessment. Whether you’re working with probability models, analyzing data distributions, or calculating confidence intervals, understanding the core equations and knowing how to apply them is fundamental. Below are some of the most important formulas to review before attempting the fourth section of the course.
Probability Formulas
Probability is central to many problems in this portion of the course. Some of the key formulas you should be familiar with include:
- Conditional Probability: P(A|B) = P(A ∩ B) / P(B)
- Multiplication Rule: P(A ∩ B) = P(A) * P(B|A)
- Addition Rule: P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Confidence Intervals and Hypothesis Testing
In the realm of inference, understanding how to calculate confidence intervals and perform hypothesis tests is crucial. Common formulas include:
- Confidence Interval for a Mean: CI = x̄ ± (Z * (σ/√n))
- Test Statistic for a Proportion: Z = (p̂ – p) / √[p(1-p)/n]
- P-value Calculation: P-value = P(test statistic ≥ observed value) under the null hypothesis
By mastering these formulas and their applications, you’ll be better equipped to handle the questions that involve both numerical and conceptual understanding.
Sample Questions with Detailed Answers
Practicing with example questions is a great way to reinforce your understanding and prepare for the assessment. In this section, we will go over several sample problems, providing detailed explanations for each solution. By working through these examples, you can better understand the steps involved and the reasoning needed to arrive at the correct solution.
Question 1: Probability Calculation
Question: A bag contains 5 red balls, 3 blue balls, and 2 green balls. If one ball is drawn at random, what is the probability that it is either red or green?
Solution: To solve this, we first calculate the total number of balls, which is 5 + 3 + 2 = 10. The number of favorable outcomes (red or green balls) is 5 (red) + 2 (green) = 7. The probability is the ratio of favorable outcomes to total outcomes:
- Probability: P(red or green) = 7/10
Question 2: Confidence Interval for a Mean
Question: A sample of 30 students was surveyed to determine the average number of hours spent studying per week. The sample mean is 15 hours, and the population standard deviation is 4 hours. Calculate the 95% confidence interval for the mean number of hours studied.
Solution: To calculate the confidence interval, we use the formula:
- Confidence Interval: CI = x̄ ± (Z * (σ/√n))
Where:
- x̄ is the sample mean = 15 hours
- σ is the population standard deviation = 4 hours
- n is the sample size = 30
- Z is the Z-value for a 95% confidence level = 1.96
Now, we calculate the margin of error:
- Margin of error = 1.96 * (4 / √30) ≈ 1.44
Thus, the confidence interval is:
- CI = 15 ± 1.44, or (13.56, 16.44)
So, the 95% confidence interval for the average number of hours studied is between 13.56 and 16.44 hours.
Important Theorems for AP Test 4B
Understanding key theorems is essential for solving complex problems in the course. These fundamental principles provide the foundation for many questions and offer insight into how to approach different types of problems. Below are some of the most important theorems you should review to enhance your problem-solving skills and succeed in the evaluation.
Central Limit Theorem
The Central Limit Theorem is a cornerstone of inferential analysis. It states that for large sample sizes, the sampling distribution of the sample mean will be approximately normally distributed, regardless of the shape of the population distribution. This theorem is especially useful when working with sample means and is key for calculating confidence intervals and performing hypothesis tests.
Law of Large Numbers
The Law of Large Numbers states that as the sample size increases, the sample mean will get closer to the population mean. This theorem underscores the reliability of sample statistics as estimators of population parameters when the sample size is sufficiently large.
| Theorem | Key Concept | Application |
|---|---|---|
| Central Limit Theorem | Sampling distribution of the mean approaches normality as the sample size increases | Used in hypothesis testing, confidence intervals, and estimating population parameters |
| Law of Large Numbers | Sample mean becomes closer to the population mean with a larger sample size | Used to estimate population parameters accurately as the sample size grows |
Familiarizing yourself with these theorems, along with their applications, will enhance your understanding and ability to tackle complex problems during the assessment.
How to Study for Test 4B
Preparing for an evaluation that tests your understanding of key concepts requires a strategic approach. It’s important to focus on the areas that are most heavily tested, while also reinforcing the foundational principles. The following tips and strategies will help guide your study sessions and ensure you’re well-prepared for the challenges ahead.
1. Review Core Concepts
Start by revisiting the most important topics that are frequently covered. Focus on concepts such as probability models, data interpretation, and inferential techniques. Reviewing these areas will help you solidify your understanding and ensure you can apply them effectively in various problems.
2. Practice with Real Questions
One of the best ways to prepare is by practicing with sample questions that mimic the types of problems you’ll encounter. Working through these examples will help you understand the structure of the questions, refine your problem-solving skills, and improve your ability to work under timed conditions.
Tip: Make sure to carefully analyze your mistakes and understand why the correct answers are what they are. This will help you avoid repeating errors on the actual evaluation.
Bonus tip: Group study sessions can be beneficial as they allow you to discuss complex problems with peers and learn from different perspectives.
Examining Data Distributions in 4B
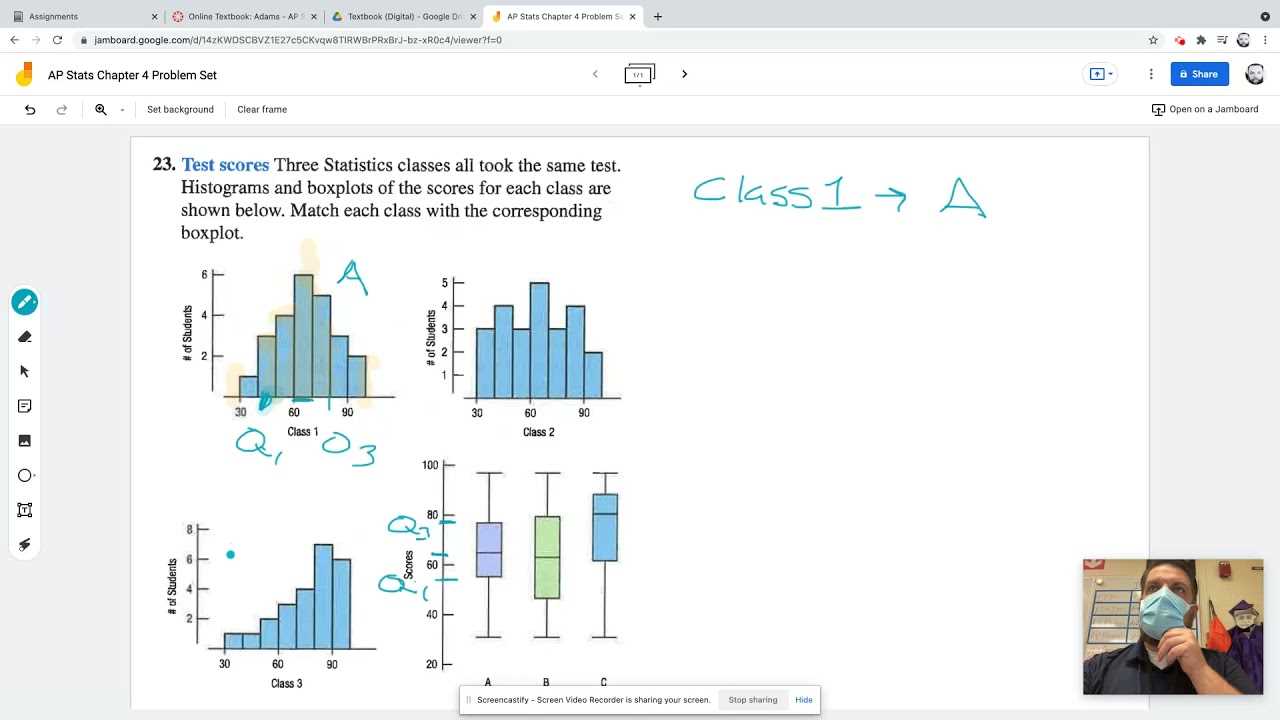
Analyzing data distributions is a critical aspect of interpreting datasets and drawing meaningful conclusions. Understanding the patterns within a dataset allows you to make informed predictions and decisions. In this section, we will explore the methods used to assess and describe various data distributions and how they are applied to real-world problems.
When working with distributions, it’s important to identify key characteristics such as central tendency, spread, and the shape of the distribution. These features help determine how the data behaves and provide insights into its underlying patterns. Common techniques for analyzing distributions include graphical representations like histograms and boxplots, as well as numerical measures like mean, median, and standard deviation.
By examining the structure of the data, you can identify potential outliers, trends, and areas that may require further investigation. This approach is essential for making accurate predictions and understanding the variability within the dataset.
Using Technology for Test 4B
Leveraging modern tools and software can significantly enhance your ability to analyze data, perform calculations, and visualize results efficiently. In this section, we will explore how technology can be used to streamline your preparation and help you perform better during the evaluation.
1. Graphing Calculators and Software
Graphing calculators and specialized software are powerful assets when it comes to solving complex problems and visualizing data distributions. Tools like TI-84 or software such as GeoGebra or Desmos can assist with creating graphs, running simulations, and calculating statistical measures. These tools allow you to:
- Quickly compute means, variances, and standard deviations
- Generate histograms, scatterplots, and boxplots for data analysis
- Simulate random samples and conduct hypothesis tests
2. Online Resources and Simulators
There are various online platforms that provide interactive lessons, practice problems, and simulations to help you build your skills. Websites like Khan Academy, Coursera, or Quizlet offer tutorials on specific topics and practice exercises. These resources allow you to:
- Engage in self-paced learning and reinforce concepts
- Access a wide variety of practice questions and solutions
- Explore dynamic simulations to deepen understanding of key principles
By utilizing these technological tools, you can improve both the efficiency and accuracy of your preparation, allowing you to focus more on critical thinking and less on manual calculations.
Time Management Tips for Test 4B
Effective time management is essential for success in any evaluation, especially when it involves solving complex problems under a time constraint. Properly managing your time during the assessment allows you to allocate sufficient attention to each section, reducing stress and improving performance. In this section, we will provide practical tips to help you manage your time efficiently during the assessment.
1. Prioritize Questions
One of the best strategies for managing your time effectively is to prioritize your tasks. Start by quickly scanning the entire assessment to identify the easier questions. Tackle these first to build confidence and secure early points. Then, move on to more difficult or time-consuming tasks. This approach ensures that you don’t get stuck on a single problem for too long.
- Quickly assess which questions can be answered with minimal effort.
- Leave more complex questions for later, giving them ample time if needed.
- Ensure that you answer all questions, even if you need to make an educated guess on the more difficult ones.
2. Set Time Limits for Each Section
Time limits can help prevent spending too much time on any one section. Break the total time into blocks based on the number of questions or the sections within the evaluation. Allocate time for each part of the assessment and stick to it, ensuring that you don’t exceed the limit for any single section.
- Divide the total available time by the number of sections to allocate an appropriate amount of time to each.
- Use a stopwatch or timer to track your progress and stay on schedule.
- Don’t dwell too long on any one problem–move forward and come back to it if time allows.
3. Practice Time-Constrained Simulations

Before the actual assessment, it’s beneficial to simulate real exam conditions by practicing under time constraints. Set aside time to complete practice exercises or previous assessments within the allotted time. This will help you get comfortable with the pace and learn to manage time more effectively.
- Use online resources or past papers to simulate timed conditions.
- Track your progress and evaluate which areas of the assessment slow you down.
- Refine your strategy by practicing how to allocate your time across different sections.
By mastering time management, you can ensure that you have enough time to complete the entire evaluation, check your answers, and submit your work confidently.
Interpreting Statistical Graphs in 4B
Understanding and analyzing graphical representations of data is a crucial skill for success in the evaluation. These visual tools help to quickly identify patterns, trends, and relationships within the data, which are essential for drawing accurate conclusions. This section will provide guidance on how to effectively interpret various types of charts and graphs presented in the evaluation.
1. Analyzing Distribution Shapes
When faced with a graphical representation, the first step is to observe the overall shape of the data distribution. This will help you understand the central tendency, spread, and any potential outliers. Pay attention to the symmetry, skewness, or clusters of the data points, as these features can reveal important insights about the dataset.
- Look for symmetry or skewness in the distribution.
- Note any unusual gaps or clusters that might suggest specific trends or anomalies.
- Identify any potential outliers that could affect the overall interpretation.
2. Understanding Summary Measures
In addition to visual inspection, statistical measures such as the mean, median, mode, range, and standard deviation are often included on graphs. These numbers provide a more precise understanding of the data’s characteristics and can help you make more informed conclusions. Make sure to recognize these measures and how they align with the visual pattern of the graph.
- Examine the central value and spread of the data.
- Consider how the summary measures compare to the shape of the graph (e.g., a mean that is higher than the median suggests a right-skewed distribution).
- Understand how outliers might affect the measures and the overall interpretation of the graph.
By mastering these skills, you can quickly and accurately extract meaningful information from graphical representations, making data interpretation much more straightforward.
Tips for Mastering Hypothesis Testing
Hypothesis evaluation is a critical skill in analyzing data and drawing valid conclusions. By following a structured approach and understanding key concepts, you can confidently assess data claims and test assumptions. In this section, we will explore strategies to improve your ability to handle hypothesis-related problems efficiently and accurately.
Mastering the art of hypothesis testing involves understanding the procedure, interpreting the results correctly, and knowing when and how to apply statistical tools. Below are several practical tips to enhance your proficiency in this area.
1. Understand the Steps Involved
The first step in hypothesis evaluation is to clearly define the null and alternative hypotheses. It’s essential to know the context of the claim and the data you are working with. The general steps to follow are:
- State the hypotheses (null vs. alternative).
- Select the appropriate significance level (α). Typically, α = 0.05 is used.
- Choose the right statistical test based on the data type (e.g., z-test, t-test).
- Calculate the test statistic using the sample data.
- Determine the p-value and compare it with the significance level to decide whether to reject the null hypothesis.
2. Familiarize Yourself with Common Test Types
Different types of tests are used to evaluate different hypotheses. Each test has its own assumptions and applicable scenarios. Familiarizing yourself with these test types will improve your ability to select the right one for each situation. Here’s a brief overview of some common tests:
| Test Type | Purpose | Use Case |
|---|---|---|
| Z-Test | Compare a sample mean to a population mean | Used when population variance is known and sample size is large |
| T-Test | Compare a sample mean to a population mean | Used when population variance is unknown and sample size is small |
| Chi-Square Test | Test relationships between categorical variables | Used in contingency tables for categorical data |
| ANOVA | Compare means across multiple groups | Used when comparing more than two groups |
3. Know How to Interpret P-Values
One of the most important aspects of hypothesis testing is understanding the p-value. The p-value represents the probability of observing data as extreme as what was observed, given that the null hypothesis is true. A p-value less than the significance level (α) indicates strong evidence against the null hypothesis, suggesting that you should reject it.
- A p-value less than 0.05 typically leads to rejecting the null hypothesis.
- A p-value greater than 0.05 suggests insufficient evidence to reject the null hypothesis.
By mastering these steps and concepts, you’ll be better equipped to perform hypothesis testing confidently and accurately in a variety of data analysis scenarios.
Understanding Confidence Intervals
Confidence intervals provide a range of values that likely contain the true value of a parameter. This concept is essential in data analysis because it offers an estimate of uncertainty, helping to gauge the reliability of the data. Instead of providing a single number as an estimate, a confidence interval gives a range that reflects possible values based on the sample data.
1. Concept of Confidence Intervals
A confidence interval is typically expressed as a lower bound and an upper bound. For example, a 95% confidence interval suggests that if the same sampling procedure is repeated many times, 95% of the intervals will contain the true parameter value. The wider the interval, the greater the uncertainty about the parameter, while a narrower interval indicates more precision.
2. Components of a Confidence Interval
The main components of a confidence interval are:
- Point Estimate: This is the sample statistic (e.g., sample mean or proportion) that serves as the best estimate of the population parameter.
- Margin of Error: This represents the amount of variability or uncertainty in the estimate and is influenced by factors like sample size and variability in the data.
- Confidence Level: This indicates the level of certainty (e.g., 95%, 99%) that the interval contains the true value.
In practice, confidence intervals allow for a more informed decision-making process by providing not just a point estimate, but a range of values that reflect potential variation in the true parameter. Understanding how to calculate and interpret these intervals is crucial for making accurate inferences in data analysis.
Preparing for the Test Day

Preparation for an important evaluation is crucial to ensure you are mentally and physically ready. The day before and the morning of the assessment are essential for setting yourself up for success. The key is to have a structured plan that includes reviewing material, staying calm, and being well-prepared for the challenges ahead.
1. Review Key Concepts
In the final hours leading up to the exam, it’s important to focus on core principles and formulas. Avoid cramming too much new material. Instead, consolidate what you already know. Here are some effective strategies:
- Quick Review: Go over important formulas and concepts you expect to encounter.
- Practice Problems: Work through a few sample questions to reinforce your understanding and identify areas that need more attention.
- Concept Maps: Create visual aids that connect related ideas, helping to clarify complex relationships between topics.
2. Organize Your Materials
Ensure that you have all the necessary materials ready the night before the exam. This will save you time and reduce stress on the morning of the assessment:
- Required Items: Check that you have the necessary tools such as a calculator, pencils, erasers, and identification.
- Comfortable Clothing: Dress in layers so you can adjust to the room temperature as needed.
- Snacks and Water: Prepare some light snacks and bring a bottle of water to stay hydrated during the exam.
3. Rest and Relax
Don’t underestimate the importance of rest. A good night’s sleep is essential for optimal performance. Try to relax and avoid last-minute stressors. Here are some tips to help you unwind:
- Relaxing Activity: Engage in a calming activity such as reading, meditating, or listening to soothing music.
- Sleep: Aim for at least 7-8 hours of sleep to ensure you’re rested and focused.
- Avoid Overthinking: Trust the preparation you’ve done and let go of unnecessary anxiety.
By following these steps, you’ll feel more confident and ready to approach the exam with a calm and focused mindset. Preparation, organization, and self-care all play a role in helping you perform at your best on the day of the evaluation.