The Practice of Statistics 3rd Edition Case Closed Answers

In this section, we explore how to tackle challenging exercises related to interpreting and analyzing data. These tasks provide an opportunity to apply theoretical knowledge to real-world scenarios, enhancing your problem-solving skills. The goal is to help you understand the process of drawing conclusions from data, recognizing patterns, and using appropriate methods to solve problems.

By examining a variety of sample problems, you’ll learn how to approach each step methodically, ensuring accurate results. Emphasis is placed on breaking down complex issues into manageable parts, utilizing different techniques, and understanding the underlying principles that guide each solution. The journey through these exercises will boost your confidence in dealing with data-driven tasks and sharpen your analytical thinking.

The Practice of Statistics 3rd Edition Case Closed Answers

This section provides a comprehensive guide to solving the various exercises presented throughout the textbook. By examining a diverse set of problems, you will gain a deeper understanding of how to apply mathematical methods to interpret data and make informed conclusions. These tasks are designed to test your ability to break down complex problems and approach them with a systematic, logical mindset.

Each problem presents a unique challenge, offering an opportunity to refine your skills in handling numbers, graphs, and statistical concepts. Through careful examination, you can learn how to accurately interpret data sets and select the appropriate techniques for each situation.

• Identify key data points and variables
• Understand relationships between variables and their influence on results
• Apply suitable methods for analyzing data trends
• Recognize common pitfalls and mistakes to avoid

By working through these problems, you’ll enhance your ability to make data-driven decisions and improve your analytical capabilities. This practice will also support your development of a deeper understanding of statistical principles and their real-world applications.

1. Start by thoroughly reading each problem and identifying what is being asked
2. Break down the problem into smaller, more manageable sections
3. Apply appropriate formulas and techniques to arrive at a solution
4. Check your work to ensure accuracy and consistency

Successfully completing these exercises will not only improve your problem-solving abilities but also build confidence in using statistical tools effectively.

Overview of the Case Closed Section

This section focuses on applying learned techniques to solve practical problems involving data analysis and interpretation. It presents a series of challenges designed to test your understanding and ability to make informed decisions based on information provided. Each task encourages the development of critical thinking, as it requires you to identify patterns, relationships, and trends within the data.

By completing these exercises, you will be able to demonstrate how well you can apply concepts to real-world situations. The problems are intended to bridge the gap between theory and practice, making sure you not only grasp the methods but also understand how to use them effectively.

Key Objectives of This Section

• Apply theoretical knowledge to solve complex problems
• Identify relevant variables and understand their interactions
• Enhance skills in interpreting and visualizing data

Skills Developed Through This Section

• Critical thinking in problem-solving
• Accuracy in applying mathematical techniques
• Effective communication of results and conclusions

Incorporating both quantitative and qualitative analysis, this section provides a well-rounded approach to mastering essential concepts in data-driven decision making. It is an essential resource for improving your proficiency and confidence in handling complex analytical tasks.

Key Concepts in Statistics Explained

Understanding fundamental ideas is crucial for successfully interpreting and analyzing data. In this section, we explore essential concepts that form the backbone of any data analysis, from interpreting data sets to applying specific methods for drawing conclusions. These core principles guide the process of making sense of numbers, variables, and relationships within data, enabling clear, accurate results.

These key ideas not only help with solving problems but also serve as the foundation for more complex techniques. Gaining a strong grasp of them is essential for anyone looking to advance their skills in working with data in various fields.

Important Statistical Terms

Term	Definition
Mean	The average value of a data set, calculated by summing all values and dividing by the number of values.
Median	The middle value in a data set when the values are arranged in order.
Mode	The value that appears most frequently in a data set.
Variance	A measure of how far each number in a data set is from the mean, showing data spread.
Standard Deviation	The square root of the variance, indicating the spread of data points around the mean.

Applying Core Principles in Analysis

• Recognizing how central tendency measures (mean, median, mode) influence conclusions
• Understanding the importance of data distribution and variability (variance, standard deviation)
• Using probability to predict future events and quantify uncertainty

Mastering these basic ideas not only simplifies complex data problems but also enhances the ability to analyze information effectively in various practical situations.

Step-by-Step Solutions for Common Problems

In this section, we break down how to approach typical challenges encountered when working with data analysis. By following a clear, step-by-step process, you can efficiently solve complex problems, ensuring you cover all essential aspects from identifying variables to interpreting results. This methodical approach helps prevent common errors and builds confidence in solving similar problems independently.

By focusing on logical steps and providing structured guidance, we aim to make the problem-solving process more accessible and understandable. Each solution is designed to build upon foundational concepts, allowing for a smooth progression through various techniques and methods.

General Approach to Solving Problems

• Start by thoroughly reading the problem to understand its requirements.
• Identify all relevant data points, variables, and conditions.
• Determine which methods or formulas are best suited for the task.
• Break down the problem into manageable parts to avoid confusion.
• Perform calculations carefully and verify each result along the way.
• Review the final solution to ensure it answers the original question correctly.

Example Problem Breakdown

1. Read through the problem statement and identify key information.
2. Define the variables and understand the relationships between them.
3. Choose the appropriate formulas or techniques based on the problem’s context.
4. Carry out the necessary calculations step by step.
5. Double-check all work for consistency and accuracy before presenting the solution.

Following these steps consistently will ensure that you approach problems logically and solve them with confidence, while minimizing the risk of errors and misinterpretations.

Understanding Statistical Methods in Practice

Applying mathematical and analytical techniques to real-world data is essential for drawing meaningful conclusions. This section explores how to use various methods in solving practical problems, providing a foundation for understanding how these approaches work outside the classroom. From analyzing data trends to testing hypotheses, each method has its specific application that can lead to clearer insights when used correctly.

By understanding the principles behind each technique, you can better decide which method is appropriate for different types of problems. Whether it’s using regression analysis to predict outcomes or calculating confidence intervals to assess uncertainty, the goal is to make informed decisions based on solid data.

In practice, these techniques are often used in combination to address complex issues. Learning to apply them correctly in context is key to achieving accurate and reliable results.

How to Approach Case Closed Exercises

Successfully tackling these exercises requires a methodical approach that breaks down the problem into smaller, more manageable parts. By following a logical sequence, you can better understand the problem at hand and apply the correct techniques to reach a solution. These exercises are designed to test your ability to think critically and apply learned concepts in practical scenarios.

Start by thoroughly reading the problem to grasp the key details and requirements. From there, systematically apply the appropriate analytical methods to extract meaningful information. This approach ensures that you address all aspects of the problem without missing any important steps.

Steps to Solve Exercises Effectively

• Read the problem carefully to understand what is being asked.
• Identify the key variables and data points provided.
• Determine which methods or formulas are required for solving the problem.
• Organize the information logically before proceeding with calculations.
• Check intermediate results to ensure accuracy throughout the process.
• Review your final solution and confirm it addresses the original question.

Tips for Successful Problem-Solving

1. Break down complex problems into smaller, more manageable sections.
2. Don’t rush through calculations; take the time to double-check your work.
3. Stay organized and keep track of your steps to avoid confusion.
4. If stuck, revisit the problem’s context and look for alternative approaches.

By following these steps and tips, you can approach each exercise with confidence, ensuring that you arrive at the correct solution while minimizing the risk of mistakes.

Common Mistakes and How to Avoid Them

When working through exercises involving data analysis and interpretation, it’s easy to make certain errors that can lead to incorrect results. Recognizing these common pitfalls is key to improving accuracy and efficiency. By understanding where mistakes often occur, you can take proactive steps to avoid them and ensure your solutions are both reliable and well-supported.

This section highlights some frequent missteps and offers practical advice on how to avoid them, making your problem-solving process smoother and more effective. By keeping these tips in mind, you can prevent errors that might otherwise compromise your results.

Frequent Errors in Data Analysis

• Misinterpreting the problem statement or overlooking important details.
• Using the wrong formula or method for the type of data presented.
• Overlooking assumptions that should be made based on the given context.
• Failing to check intermediate steps for calculation errors.
• Ignoring the need for data verification or validation before concluding results.

How to Avoid These Mistakes

• Read the problem thoroughly to ensure a clear understanding of the requirements.
• Double-check the selected methods and formulas to ensure they match the context of the data.
• Verify all assumptions before proceeding with calculations.
• Keep careful track of each step and perform intermediate checks for accuracy.
• Review the final solution to ensure it answers the question appropriately and accurately.

By staying vigilant and following these best practices, you can avoid many common mistakes and improve the overall quality of your analysis.

Analyzing Data Using the Right Techniques

Choosing the correct approach for data analysis is crucial to obtaining meaningful insights. By selecting the most appropriate method for the specific type of data and research question, you can ensure accurate results and avoid misinterpretation. Different techniques are suited for different situations, and understanding when to apply each one is key to effective problem-solving.

In this section, we will explore how to evaluate data and select the best techniques for analyzing it. This understanding allows for deeper insights and ensures that conclusions drawn from the analysis are well-supported by the data.

Choosing the Right Method for Your Data

• Examine the nature of the data–whether it is categorical or numerical–before choosing an analysis method.
• For relationships between variables, consider using correlation or regression techniques.
• If comparing groups, look into t-tests, ANOVA, or chi-square tests based on the type of data.
• When dealing with uncertainty, use probability distributions to model and predict outcomes.
• For large datasets, consider data visualization techniques to identify trends and patterns more clearly.

Common Techniques for Data Analysis

• Regression Analysis: A method for identifying relationships between dependent and independent variables.
• Descriptive Statistics: Summarizes and describes key features of the dataset, such as mean, median, and standard deviation.
• Hypothesis Testing: Used to determine the validity of a hypothesis based on sample data.
• Data Visualization: Creating graphs, charts, and plots to visually represent data and trends.

By applying the correct technique to each situation, you can gain clear, accurate insights from your data and make well-informed decisions based on the analysis.

Applying Real-World Scenarios to Statistics

Bringing theoretical concepts into real-world applications is essential for understanding their practical value. By applying analytical methods to actual situations, you can gain a deeper understanding of how they function and help make informed decisions. Real-world scenarios provide context that makes abstract concepts more tangible and relevant.

This section explores how to connect mathematical techniques to real-life problems. By examining case studies and examples from various industries, you’ll see how different methods are used to interpret data, test hypotheses, and make predictions in fields ranging from healthcare to business.

Real-World Applications in Business

In the business world, data analysis is frequently used to identify trends, improve processes, and predict customer behavior. Some examples include:

• Using regression analysis to forecast sales and growth trends.
• Applying hypothesis testing to determine the effectiveness of marketing campaigns.
• Utilizing probability distributions to assess financial risks and make investment decisions.

Applications in Healthcare and Medicine

In healthcare, statistical methods are crucial for analyzing patient outcomes, testing new treatments, and improving medical practices. Common uses include:

• Conducting clinical trials to test the effectiveness of new medications or procedures.
• Applying statistical models to predict disease outbreaks and patient needs.
• Analyzing survey data to understand public health trends and behaviors.

By using these methods in real-world contexts, we can see their practical utility and the ways they support decision-making across various sectors.

Why Case Closed Exercises are Important

Engaging with practical exercises that simulate real-world problems is essential for developing strong analytical skills. These activities allow individuals to apply theoretical knowledge in a structured way, reinforcing key concepts and improving problem-solving abilities. By working through these tasks, learners can bridge the gap between theory and application, gaining deeper insights into data analysis.

These exercises offer more than just practice–they challenge participants to think critically, analyze data from multiple perspectives, and refine their approach to solving complex problems. Through consistent application, individuals build a stronger foundation for tackling real-life situations and making data-driven decisions.

Moreover, such tasks help develop essential skills like attention to detail, logical reasoning, and the ability to interpret data effectively. Whether preparing for exams or honing professional skills, these exercises are crucial for mastering the necessary techniques and methodologies in analytical fields.

Tips for Mastering the Practice Problems

Mastering practice problems is a crucial step in gaining proficiency in analytical techniques. These exercises help solidify your understanding of core concepts and improve your ability to solve complex problems under different conditions. By following a structured approach and applying the right strategies, you can enhance both your comprehension and problem-solving speed.

This section offers actionable tips to help you excel at tackling practice exercises. By breaking down problems into manageable steps, reviewing solutions carefully, and seeking out additional resources when needed, you can strengthen your skills and build confidence.

Approach Problems Step by Step

• Start by reading each problem carefully to understand the context and requirements.
• Identify the key variables and concepts involved, highlighting important information.
• Break the problem into smaller tasks, tackling each one before moving to the next.
• Check your work as you progress to avoid missing critical steps or making errors.

Review and Learn from Mistakes

• After completing each problem, carefully review the solution to understand the methodology behind it.
• Take note of any mistakes and try to pinpoint where your understanding or approach went wrong.
• Revisit similar problems to reinforce correct strategies and avoid repeating errors.
• Seek out additional examples to practice and expand your understanding of various techniques.

With consistent practice and a focused approach, mastering these exercises will help you develop a strong command of key concepts and improve your problem-solving skills significantly.

Breaking Down the Complex Cases

When faced with intricate problems, it’s easy to feel overwhelmed. However, breaking these challenges down into smaller, more manageable parts can help you approach them with confidence. By deconstructing a complex scenario step by step, you can focus on each element individually, making it easier to analyze and solve.

In this section, we will explore strategies for tackling complex problems by simplifying them and applying systematic methods. By learning to identify key components, using appropriate techniques, and organizing your work effectively, you’ll be able to navigate through even the most complicated exercises.

Identifying Key Elements

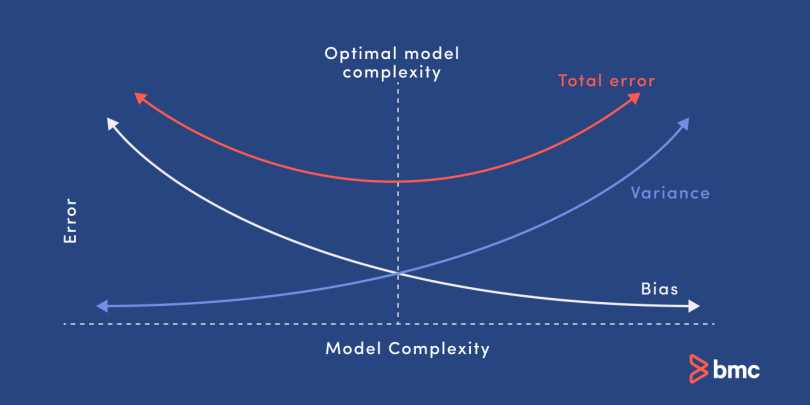
Before diving into calculations or interpretations, take a moment to carefully read through the problem. Look for the following:

• Key variables: Identify the important numbers or factors that will affect the outcome.
• Required outcomes: Understand what the question is asking for–whether it’s a specific value, trend, or relationship.
• Conditions and assumptions: Note any limitations or constraints that must be factored into the solution process.

Applying Methodical Approaches

Once you’ve identified the crucial elements, it’s time to apply the appropriate techniques. Some useful steps include:

• Break the problem into smaller chunks: Solve each part independently, then combine the results.
• Use visual aids: Diagrams, tables, and charts can help clarify complex relationships and data patterns.
• Work backward: If you’re stuck, sometimes it helps to reverse-engineer the problem to understand the required steps more clearly.

By systematically approaching complex challenges, you can improve your ability to break down and solve difficult problems with greater efficiency and accuracy.

Understanding Statistical Significance in Context

Interpreting results correctly is essential for making informed decisions based on data. Statistical significance is a key concept in evaluating whether the observed outcomes are likely due to a real effect or simply due to random chance. However, understanding its relevance goes beyond just calculating p-values–it requires considering the broader context of the problem, the data, and the potential implications of the results.

This section explores how to assess statistical significance with context in mind. It’s not enough to rely solely on numbers; interpreting those numbers in relation to the real-world situation they represent is just as crucial. By understanding how significance fits into the bigger picture, you can make more informed conclusions.

Interpreting P-Values Correctly

P-values help us determine the likelihood of obtaining results at least as extreme as the observed results, assuming that the null hypothesis is true. However, a small p-value doesn’t always mean a result is practically significant. Consider the following:

• Threshold for significance: While a p-value of 0.05 is often used as the threshold, context matters. In some fields, a more stringent threshold, like 0.01, may be necessary.
• Sample size: A large sample size may produce a statistically significant result, but it doesn’t automatically mean the result is important or meaningful in practical terms.
• Effect size: A statistically significant result with a very small effect may not have meaningful real-world implications, despite its statistical validity.

Evaluating Results in Context

Contextual factors are essential in interpreting statistical significance. Here are a few considerations to keep in mind:

• Relevance to the field: In some disciplines, even small effects can be important if they have real-world consequences.
• Data quality and assumptions: Ensure that the data assumptions, such as normality or independence, are met before drawing conclusions from significance tests.
• Practical implications: Beyond statistical significance, evaluate whether the result will lead to changes in practice, policy, or understanding.

By integrating these factors into your interpretation of statistical results, you can make better, more meaningful conclusions that take both the statistical evidence and the context into account.

Using Technology to Solve Statistical Problems

Advancements in technology have significantly improved how we approach and solve complex data problems. Tools and software designed for data analysis allow users to process large datasets quickly, apply sophisticated algorithms, and visualize results in a meaningful way. These innovations not only streamline calculations but also enhance the accuracy of statistical inferences and the interpretation of results.

Technology empowers researchers, analysts, and students to explore and solve problems that would have been tedious or impossible to tackle manually. From automated calculations to visualizing trends, these tools have become indispensable in modern data analysis.

Software Tools for Data Analysis

Several software programs are available to help in solving statistical problems. These programs provide a wide range of features, such as regression analysis, hypothesis testing, and data visualization. Some popular options include:

• Excel: Widely accessible, Excel is a powerful tool for basic analysis, including generating charts, performing t-tests, and regression analysis.
• R: An open-source programming language and environment for statistical computing, R is particularly useful for advanced modeling and visualizations.
• SPSS: A user-friendly platform designed for both beginners and experts, SPSS is commonly used for statistical analysis in social sciences and healthcare research.
• Python (with libraries like Pandas and SciPy): A versatile programming language, Python, with the help of libraries, is used for performing complex analyses, from simple calculations to machine learning models.

Advantages of Using Technology

Incorporating technology into statistical analysis offers numerous benefits:

• Efficiency: Automating calculations and analyses saves time and reduces the potential for human error, allowing for faster problem-solving.
• Accuracy: Algorithms and software are designed to minimize mistakes, ensuring precise results that are crucial for decision-making.
• Advanced Techniques: Technology opens the door to complex methods like machine learning, simulations, and multivariate analysis that would be nearly impossible to perform by hand.
• Data Visualization: Modern tools provide powerful data visualization capabilities, enabling users to present findings in an easily interpretable format.

By leveraging technology, statistical problem-solving becomes more effective, accessible, and insightful, transforming raw data into meaningful conclusions with ease.

Improving Accuracy in Statistical Answers

Achieving precision in data interpretation is essential for making informed decisions. In any analysis, errors can arise at various stages, from data collection to interpretation. It’s crucial to use reliable methods, tools, and practices to minimize inaccuracies. Ensuring that calculations are correct and assumptions are valid strengthens the integrity of conclusions drawn from the data.

Enhancing precision requires attention to detail, knowledge of relevant techniques, and careful application of tools designed to handle complex calculations. Whether working with large datasets or small sample sizes, every step in the process plays a role in ensuring reliable results.

Key Strategies for Improving Accuracy

To enhance the accuracy of statistical results, consider the following strategies:

• Use Reliable Data: Ensure that the data used for analysis is accurate and free from errors. Clean the data by checking for missing values, outliers, or inconsistencies.
• Choose the Right Methods: Different problems require different techniques. Selecting the most appropriate statistical method is crucial for obtaining accurate results.
• Verify Assumptions: Many statistical methods are based on assumptions (e.g., normality of data). Validating these assumptions before proceeding ensures that the chosen methods are applicable.
• Double-Check Calculations: Manual calculations or software-generated results should be verified, especially for complex problems. Small errors in computation can lead to incorrect conclusions.
• Use High-Quality Software: Employing tools and software known for their precision, such as R, Python, or SPSS, helps reduce errors in calculations and analysis.

Common Pitfalls to Avoid

While striving for accuracy, be aware of common mistakes that can compromise the integrity of statistical work:

• Overfitting: When a model is too complex, it may fit the training data very well but fail to generalize to new data. Striking a balance between simplicity and complexity is key.
• Ignoring Outliers: Outliers can skew results, but in some cases, they carry valuable information. Analyzing outliers properly can improve the accuracy of the findings.
• Misinterpreting Results: Be cautious when drawing conclusions from statistical results. Correlation does not imply causation, and care should be taken not to overgeneralize findings.

By following best practices and carefully considering potential sources of error, one can significantly improve the accuracy of results and enhance the overall reliability of statistical analyses.

Advanced Problem-Solving Strategies

Approaching complex problems requires more than just basic understanding; it demands strategic thinking, careful analysis, and a methodical approach. Advanced techniques can help break down intricate issues into manageable components and offer insights that lead to effective solutions. Mastering these strategies allows individuals to tackle challenging problems with confidence and precision, whether working with large datasets, intricate patterns, or abstract concepts.

In order to excel in these tasks, one must employ a combination of logical reasoning, creative approaches, and reliable tools to uncover patterns and make well-informed decisions. Below are some key strategies to consider when dealing with advanced-level problems.

Key Techniques for Advanced Problem-Solving

Strategy	Description
Breaking Down the Problem	Decompose a complex issue into smaller, more manageable parts. Solving smaller sections can simplify the overall solution and reduce the chances of missing important details.
Hypothesis Testing	Formulate potential solutions based on the information available, then test these hypotheses to verify or eliminate them based on evidence.
Iteration	Refine solutions step by step. Iterative testing allows for gradual improvements, and helps in identifying errors early in the process.
Utilizing Algorithms	Implement algorithms or computational methods to process large volumes of data, identifying trends or patterns that may be difficult to spot manually.
Modeling and Simulation	Use models or simulations to represent real-world situations, testing different scenarios and understanding potential outcomes without actual experimentation.

Optimizing Solutions Through Analytical Tools

To maximize efficiency, advanced problem-solvers rely on various analytical tools. These include software applications that help in performing computations, graphing trends, and even automating parts of the process. Here are some commonly used tools:

• Mathematical Software: Tools like MATLAB or Mathematica provide advanced capabilities for solving mathematical problems.
• Programming Languages: Python, R, and other coding languages enable users to write custom algorithms and automate repetitive tasks.
• Statistical Packages: SPSS, SAS, and Stata are commonly used for complex statistical analysis, offering built-in functions for hypothesis testing, regression, and modeling.
• Data Visualization: Tools like Tableau and Power BI allow users to create interactive visualizations, making it easier to interpret and present complex data.

By mastering these advanced strategies and tools, problem-solvers can enhance their ability to tackle even the most difficult challenges effectively. The key is a combination of systematic analysis and innovative thinking, continually honing skills to stay ahead in solving complex problems.

Additional Resources for Further Learning

To gain a deeper understanding and continue developing skills in problem-solving and data analysis, a wide variety of resources are available. These resources span books, online platforms, academic courses, and interactive tools that can help enhance knowledge and provide practical experience. Exploring these options allows learners to gain different perspectives, stay updated with the latest methodologies, and improve their analytical abilities.

Recommended Books

Reading comprehensive texts on related topics can provide valuable insights and a more thorough understanding of core principles. Some well-regarded books include:

• Introduction to Mathematical Modeling – A thorough guide to building and applying mathematical models across different disciplines.
• Data Science for Business – This book offers practical advice on how to use data analysis techniques to make informed business decisions.
• R for Data Science – A comprehensive text for learning R programming, with a focus on data science applications and techniques.
• Statistical Methods for Research Workers – A classic work that introduces important statistical concepts and methods used in scientific research.

Online Platforms and Courses

Numerous websites offer free and paid courses, interactive tutorials, and video lectures that can support learners in applying concepts practically:

• Coursera: Offers online courses from top universities, covering topics like data analysis, machine learning, and applied mathematics.
• edX: Provides a wide selection of online classes on data science, analytical techniques, and related fields, many of which are free to audit.
• Khan Academy: Known for offering free resources on a wide range of subjects, including foundational courses in mathematics and data interpretation.
• Udacity: Offers in-depth programs in data science, analytics, and artificial intelligence with hands-on projects and mentoring.

By taking advantage of these resources, individuals can deepen their knowledge and enhance their skills in solving complex problems. Whether through self-paced learning or structured courses, these tools can provide the guidance needed to excel in data analysis and related fields.