In geometry, certain figures possess unique properties that make them easier to solve using specific methods. These shapes are essential for mastering various concepts, and understanding their characteristics can significantly simplify calculations. By focusing on their inherent relationships, solving them becomes a straightforward task, even for complex problems.
By analyzing the angles and proportions within these figures, students can apply simple yet powerful techniques to find unknown values. Understanding these relationships forms the foundation for a deeper grasp of geometric principles, paving the way for more advanced studies in mathematics and applied fields.
Whether you are learning the fundamentals or refining your skills, mastering these figures will help you navigate through more challenging problems with confidence. This guide provides an overview of how to approach and solve problems involving these unique shapes efficiently.
Math 2 Special Right Triangles Answers

In geometry, certain geometric figures with fixed properties offer a simplified approach to solving problems. These shapes have consistent ratios and relationships that make finding missing components much easier. By understanding how the sides and angles of these figures are related, anyone can confidently determine unknown values with minimal calculation.
For example, a common set of relationships exists between the sides of two particular shapes, where one side is always a fixed multiple of another. By memorizing these relationships, one can quickly solve for missing sides or angles. This method eliminates the need for more complex formulas and makes geometry more accessible for learners.
By mastering the basic rules and understanding the interconnections, solving geometric problems becomes a task of straightforward application. With practice, these problems become routine, and the confidence gained from consistent success builds a solid foundation for tackling more challenging concepts in mathematics.
Understanding Special Right Triangles
In geometry, some figures exhibit consistent properties that allow for easier calculation of unknown values. These shapes, often found in various fields of study, are defined by predictable patterns between their angles and side lengths. By recognizing these patterns, solving for missing parts becomes a simpler task, as certain ratios remain constant.
One of the most useful tools when working with these figures is knowing the specific relationships between the sides and angles. By understanding these connections, calculations can be performed more efficiently. The key is recognizing which shapes fall into this category and how their properties can be applied to solve geometric problems.
Key Relationships Between Sides and Angles
Here are the essential relationships that govern these figures:
| Shape | Angles | Side Length Ratios |
|---|---|---|
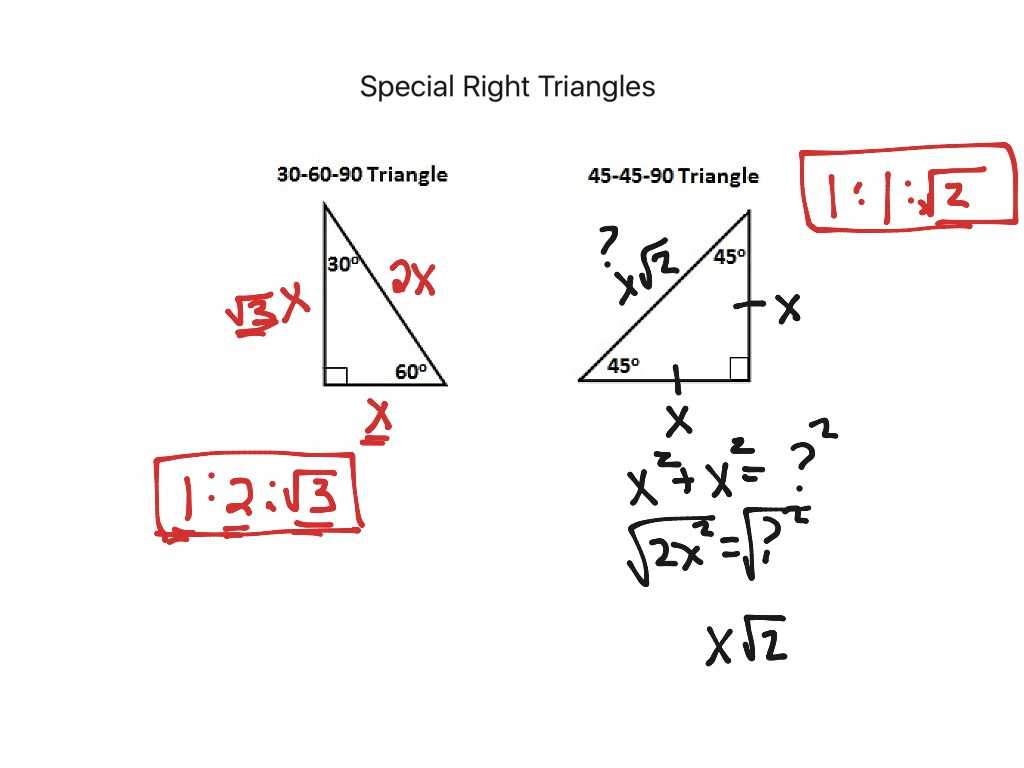
| 30-60-90 Figure | 30°, 60°, 90° | 1 : √3 : 2 |
| 45-45-90 Figure | 45°, 45°, 90° | 1 : 1 : √2 |
Practical Applications in Problem Solving
By using these established ratios, students and professionals can solve for unknown sides or angles with ease. These relationships reduce the complexity of more advanced geometric problems, offering a faster, more accurate approach to solving real-world issues. With consistent practice, these figures become a powerful tool in any geometric context.
Key Properties of 30 60 90 Triangles
In geometry, certain figures have inherent characteristics that simplify problem-solving. One such shape is defined by three specific angles, leading to consistent ratios between its sides. Understanding these properties allows for easy calculation of missing components, reducing the need for complex formulas.
The most notable feature of this particular figure is the predictable relationship between its sides. These relationships can be easily applied to find unknown side lengths, making it a valuable tool in geometry. The key to solving problems involving this shape lies in recognizing how the sides relate to one another and leveraging these ratios for quick calculations.
Side Length Ratios
The sides of this shape follow a simple ratio that can be memorized for easier calculation. If the length of the shortest side is labeled as “x,” then the longer leg is “x√3,” and the hypotenuse is “2x.” These consistent relationships make it possible to determine any missing side as long as one side is known.
Application in Problem Solving
Once the ratios are understood, they can be applied to a variety of problems, from basic geometry exercises to more advanced real-world applications. The simplicity of these relationships allows for quick and accurate results, making it an essential concept in geometry studies.
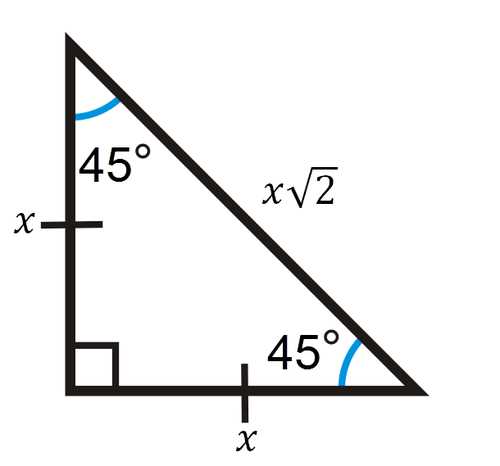
Solving 45 45 90 Triangles
When dealing with a specific type of geometric figure, understanding its inherent properties can significantly simplify problem-solving. One such shape has two equal angles, which leads to predictable relationships between its sides. Recognizing these properties allows for quick and efficient calculations, making it easier to solve for unknown values.
The most important aspect of working with this shape is the consistent ratio between its sides. These ratios remain the same regardless of the size of the figure, making it possible to find any missing side as long as one side is known. By applying this rule, solving problems becomes a straightforward process.
Side Length Ratios
The sides of this figure follow a fixed relationship. If one leg is labeled “x,” then the other leg is also “x,” and the hypotenuse is “x√2.” These ratios make it easy to calculate any side when the length of one side is provided. Here’s how the relationships work:
- Both legs are of equal length.
- The hypotenuse is √2 times the length of either leg.
Step-by-Step Guide to Solving
To solve for missing sides, follow these steps:
- Identify the length of one leg.
- Use the ratio to calculate the length of the other leg, which will be the same.
- Multiply the length of a leg by √2 to find the length of the hypotenuse.
With these simple steps, solving for unknown sides becomes a quick and reliable process. Understanding these basic relationships is key to mastering more complex geometric problems.
How to Apply the Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry that relates the sides of a specific type of shape. This theorem provides a simple method for calculating the length of one side if the lengths of the other two sides are known. By using this rule, it becomes possible to solve for missing measurements in many geometric problems.
To apply the Pythagorean theorem, you need to know the relationship between the three sides of the shape. The theorem states that the square of the length of the longest side is equal to the sum of the squares of the other two sides. This relationship holds true for any shape that fits the criteria.
Steps to Apply the Theorem
Follow these steps to use the Pythagorean theorem:
- Identify the lengths of two sides of the shape.
- Label the sides as a, b, and c, where c is the longest side (the hypotenuse).
- Use the formula a² + b² = c² to solve for the unknown side.
- Take the square root of the result to find the length of the missing side.
Example of Applying the Theorem
Consider a shape with one side measuring 3 units and the other measuring 4 units. To find the hypotenuse, apply the Pythagorean theorem:
- Square the known sides: 3² = 9 and 4² = 16.
- Add the results: 9 + 16 = 25.
- Take the square root of 25: √25 = 5.
The length of the hypotenuse is 5 units. This method can be used to find missing sides in many geometric problems involving this shape.
Finding Missing Sides in Right Triangles
In geometry, determining unknown side lengths in a specific figure can often be done by applying fundamental principles. When two sides are given, it becomes possible to calculate the length of the third side using simple mathematical relationships. This process is essential for solving many geometric problems, especially when dealing with specific shapes that follow consistent rules.
To find the missing side, it’s important to identify which sides are known and which one needs to be calculated. Depending on the given information, the Pythagorean theorem or side length ratios can be used to determine the unknown length efficiently. Understanding the basic principles that govern these shapes makes this process straightforward.
Using the Pythagorean Theorem
If two sides of the shape are known, the Pythagorean theorem can be used to find the third side. The formula a² + b² = c² relates the squares of the sides, where a and b are the legs, and c is the hypotenuse. By solving this equation, the missing side can be determined.
Using Known Ratios
In some cases, when one side is known, simple ratios can help find the missing sides. For specific shapes with equal angles, the ratios between the sides are fixed, allowing for quick calculations. These ratios are reliable tools for determining unknown lengths without complex calculations.
Trigonometric Ratios for Special Triangles
In geometry, trigonometry provides essential tools for relating the angles of a shape to the ratios of its sides. Certain shapes with specific angle measures allow for the use of these ratios in a straightforward manner. By understanding these relationships, it becomes easier to calculate missing side lengths or angles, even when some information is unknown.
The key to solving problems involving these shapes lies in applying the correct trigonometric functions. Sine, cosine, and tangent ratios can be used to determine unknown sides or angles based on the known values. These functions offer a quick and efficient way to solve for missing parts of the figure without relying on more complex formulas.
Using Sine, Cosine, and Tangent
Trigonometric ratios are based on the relationships between the sides of a shape and its angles. The basic trigonometric functions are:
- Sine (sin)>: Ratio of the opposite side to the hypotenuse.
- Cosine (cos)>: Ratio of the adjacent side to the hypotenuse.
- Tangent (tan)>: Ratio of the opposite side to the adjacent side.
By using these functions, it is possible to find unknown sides or angles if one side or angle is known. These ratios are especially helpful in solving problems involving non-right angles in specific figures.
Practical Application of Trigonometric Ratios

When solving for unknowns in these shapes, apply the appropriate trigonometric ratio based on the given information. For example, if the length of one leg and the angle are known, you can use the sine or cosine function to find the length of the other leg. With consistent practice, these ratios can become a reliable method for solving a wide range of geometric problems.
Common Mistakes in Triangle Calculations
When solving problems involving geometric shapes, errors can occur if certain principles are misunderstood or applied incorrectly. Many of these mistakes stem from confusion over formulas, misinterpretation of relationships between sides, or incorrect application of trigonometric functions. Recognizing and avoiding these common pitfalls can significantly improve accuracy and efficiency in solving geometry problems.
It’s crucial to have a clear understanding of the properties of the shapes you are working with, especially when applying formulas or performing calculations. Missteps often happen when the wrong formula is used, or when assumptions are made about side lengths or angles that don’t hold true for the given problem.
Common Calculation Errors
Here are some of the most frequent mistakes made during geometric calculations:
| Mistake | Explanation | Solution |
|---|---|---|
| Incorrectly using the Pythagorean theorem | Misapplying the theorem to shapes that do not fit the required conditions. | Ensure the shape meets the criteria for using the theorem (only applies to certain shapes with right angles). |
| Mixing up trigonometric ratios | Using the wrong function (sine, cosine, or tangent) for the given sides and angles. | Double-check which sides of the shape you have and apply the correct ratio based on the angle. |
| Assuming side lengths are equal | Incorrectly assuming two sides are equal when they are not, often in non-equilateral shapes. | Always verify side lengths before making assumptions, especially when working with non-equilateral shapes. |
How to Avoid These Mistakes
To prevent these errors, always start by carefully analyzing the problem and understanding the given information. If a formula or theorem is required, review the conditions under which it applies. Additionally, take the time to verify your calculations step by step to ensure all relationships are accurately represented.
Real-World Applications of Right Triangles
Geometric shapes with specific angle measures are commonly found in everyday life. These shapes are used in various fields, from construction to navigation, because of their simplicity and ability to model real-world problems. Understanding the principles behind these shapes allows us to apply them to solve practical problems effectively and efficiently.
Whether it’s calculating the height of a building, determining the distance between two points, or designing a structure, these geometric principles play a crucial role in making accurate measurements and decisions. The relationships between the sides and angles in these shapes help professionals in various industries carry out their tasks with precision.
Common Uses in Various Fields
Here are some ways these shapes are used in real-world applications:
- Architecture and Construction: Engineers and architects use these shapes to design stable structures, ensuring correct angles and side lengths for beams, walls, and roofs.
- Navigation and Surveying: In land surveying, these shapes are used to measure distances, angles, and create accurate maps of terrain.
- Physics: In physics, these shapes help in understanding forces, motion, and energy, especially when dealing with inclined planes or force vectors.
- Astronomy: Calculating the distance between celestial bodies often involves these geometric relationships, especially when measuring angles between stars or planets.
Practical Examples
In construction, if you need to find the height of a building and you can measure the distance from the base and the angle of elevation, you can apply the appropriate relationships to determine the height. Similarly, in navigation, when determining the shortest path between two locations on a map, these principles can help calculate the correct distance and direction.
Using the Unit Circle for Triangle Solutions
The unit circle is a powerful tool in trigonometry, providing a geometric way to understand the relationships between angles and the sides of certain shapes. It simplifies the process of finding angles and side lengths, particularly when dealing with circular motion or wave functions. By using this circle, we can calculate values for sine, cosine, and other trigonometric functions directly from the angles, making it a valuable method for solving problems in geometry and beyond.
The unit circle consists of a circle with a radius of one, centered at the origin of a coordinate plane. This setup makes it easier to relate angles and their corresponding values for trigonometric functions. Each point on the unit circle represents a specific angle, and the coordinates of that point can be used to determine the sine and cosine of that angle, which are essential for solving problems involving angles and distances.
How the Unit Circle Helps in Triangle Solutions
When working with shapes, the unit circle can simplify many calculations by providing a straightforward way to find key values like sine and cosine. These values can then be used to solve for unknown sides and angles in various types of problems. Here’s how:
- Angle Determination: By referring to the unit circle, you can quickly identify the sine and cosine values for common angles, such as 30°, 45°, and 60°, which are frequently used in geometric calculations.
- Side Lengths: The unit circle’s coordinates (cosine for the x-coordinate and sine for the y-coordinate) help determine the side lengths of geometric figures, especially when dealing with regular shapes.
- Trigonometric Functions: Using the unit circle, you can directly calculate sine, cosine, and tangent values for a wide range of angles, simplifying complex geometric problems.
Practical Applications
In real-world applications, the unit circle is commonly used in fields such as physics, engineering, and computer graphics. For example, in physics, it helps model wave motion or oscillations, while in engineering, it aids in calculations for mechanical and electrical systems. By mastering the unit circle, you gain an essential tool for solving a variety of problems efficiently and accurately.
Step-by-Step Guide to Triangle Solutions
Solving geometric problems involving specific shapes with precise angle measures can seem complex at first. However, breaking down the process into clear, manageable steps makes it much easier to solve for unknown sides and angles. Whether you are given some sides and need to find others, or you’re asked to determine angles, following a structured approach can guide you to accurate solutions.
This guide provides a systematic method for solving various problems involving geometric shapes. By focusing on key concepts and utilizing simple trigonometric principles, you can solve these problems with confidence and clarity. Below are the steps you can follow to approach most calculations.
Step-by-Step Solution Process
- Step 1: Identify Known Information
Start by reviewing the problem and identifying all the given values. This might include side lengths, angles, or specific properties of the shape. Mark these on your diagram to have a visual reference.
- Step 2: Choose the Appropriate Formula
Depending on the information you have, select the most relevant formula. For example, if you have two sides and need to find the third, use the Pythagorean theorem. If you’re solving for angles, trigonometric ratios might be more suitable.
- Step 3: Apply the Formula
Once you’ve identified the right formula, plug in the known values and perform the necessary calculations. Be sure to double-check each step to avoid errors.
- Step 4: Solve for the Unknown
With the formula applied, solve for the unknown values, such as missing angles or side lengths. If you’re using trigonometric ratios, ensure your calculator is in the correct mode (degrees or radians) to get accurate results.
- Step 5: Verify the Results
Check your results to ensure they make sense in the context of the problem. If possible, use a different method (such as the Pythagorean theorem or another trigonometric ratio) to verify your calculations.
Common Tips for Success
- Always draw a clear diagram to visualize the problem.
- When working with angles, make sure you use the correct unit (degrees or radians).
- If you’re solving for a side, ensure all calculations are done accurately before rounding off the final answer.
- Double-check the conditions of the shape (e.g., if it is isosceles or equilateral) before applying formulas.
How to Verify Triangle Answers

After solving geometric problems, it is important to verify the results to ensure accuracy. Verification helps confirm that the calculations align with known mathematical principles and that no mistakes were made during the process. By following a structured approach to checking your work, you can gain confidence in the correctness of your solution.
Verification involves comparing the obtained results with established rules or methods. Whether checking side lengths, angles, or other properties, there are a few key strategies that can help ensure your solution is correct.
Methods for Verifying Results
- Check with the Pythagorean Theorem:
If the problem involves a geometric figure with known side lengths, use the Pythagorean theorem to verify your results. If the square of the two shorter sides equals the square of the longest side, then your solution is likely correct.
- Use Trigonometric Ratios:
For problems involving angles, verify your results using trigonometric ratios. Check that the sine, cosine, or tangent of the angles match the corresponding side lengths. If the ratios hold true, then your answer is correct.
- Double-Check Calculations:
Always recheck the arithmetic involved in your solution. Simple errors like adding or subtracting incorrectly can lead to wrong answers. Ensure that each step follows logically from the previous one.
- Cross-Check with Alternative Methods:
If you used one approach to find your solution, try solving the problem using a different method to see if you get the same result. For example, if you found a side length using trigonometric ratios, try using the Pythagorean theorem as a backup check.
- Confirm with a Diagram:
Review the diagram or sketch you created when solving the problem. Verify that the results make sense visually, and that the geometric properties are consistent with the figure you are working with.
Common Pitfalls to Avoid
- Make sure the correct formula is applied for the problem type.
- Ensure that you are working with the proper angle unit (degrees or radians).
- Check that you are using the correct side lengths when applying trigonometric ratios.
Geometry Formulas for Special Triangles
In geometry, certain figures follow predictable patterns and relationships that simplify calculations. When working with specific geometric shapes, understanding the key formulas for their properties can make solving problems faster and more efficient. These formulas are particularly useful when dealing with common shapes that have consistent angle measurements and side length ratios.
Knowing the fundamental relationships between the sides and angles of these shapes allows for easier computation of unknown values, such as side lengths, angles, or areas. Whether calculating perimeter, area, or applying trigonometric principles, these essential formulas are crucial tools for solving geometric problems accurately.
Common Formulas for Area and Perimeter
- Area of an Isosceles Triangle:
The formula for the area of an isosceles triangle is: Area = (base × height) / 2. This formula works when the height is known or can be calculated using the properties of the shape.
- Perimeter of an Equilateral Triangle:
The perimeter is calculated as: Perimeter = 3 × side length. This works for any equilateral triangle where all sides are equal.
- Area of a Scalene Triangle:
For a scalene triangle, where all sides are different, the area can be found using Heron’s formula: Area = √[s(s – a)(s – b)(s – c)], where s is the semi-perimeter and a, b, c are the side lengths.
Using Trigonometric Ratios for Side Lengths

- Using Sine, Cosine, and Tangent:
In a triangle with a known angle, trigonometric ratios can help determine the lengths of the sides. For example:
- Sine: sin(θ) = opposite / hypotenuse
- Cosine: cos(θ) = adjacent / hypotenuse
- Tangent: tan(θ) = opposite / adjacent
- Pythagorean Theorem:
For any right-angled triangle, the Pythagorean theorem is a fundamental formula to calculate the length of the third side: a² + b² = c², where c is the hypotenuse and a and b are the other two sides.
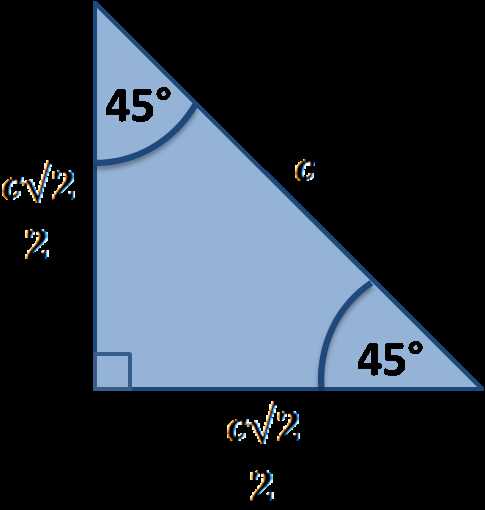
Understanding Triangle Leg and Hypotenuse Relations
In geometry, understanding the relationship between the sides of a triangle is essential for solving various problems. The longest side of a triangle, opposite the largest angle, plays a crucial role in calculations. By examining the connections between the legs (the shorter sides) and this longest side, we can uncover valuable insights about the shape’s proportions and solve for unknown values with ease.
The relationships between the legs and the hypotenuse follow specific patterns that are vital for applying key geometric principles. For example, knowing the length of one leg can often allow you to calculate the other leg or the hypotenuse, depending on the available information and the type of triangle in question.
Key Proportions in Triangles
- Leg Lengths and Hypotenuse Ratio:
In many triangles, particularly those with specific angle measurements, the ratio of the legs to the hypotenuse is consistent. For example, in a 45-45-90 triangle, both legs are of equal length, and the hypotenuse is √2 times the length of either leg.
- Leg to Hypotenuse in a 30-60-90 Triangle:
In this type of triangle, the ratio between the legs and hypotenuse is also fixed: the shorter leg is half the length of the hypotenuse, while the longer leg is √3/2 times the length of the hypotenuse.
Using Relationships to Find Unknown Sides
- Applying the Pythagorean Theorem:
For any triangle, the Pythagorean theorem allows you to find the missing side when the lengths of the other two sides are known. The formula is: a² + b² = c², where a and b are the legs, and c is the hypotenuse.
- Leg and Hypotenuse in Real-World Problems:
Understanding the relationship between the legs and hypotenuse is not just for theoretical problems; it also helps in real-world situations like construction, navigation, and design, where precise measurements are essential.
Role of Angles in Special Triangles
The angles within a triangle play a pivotal role in determining the proportions between its sides. The specific values of these angles often dictate how we approach calculations and solve for unknown lengths. Understanding how the angles interact with the sides provides insights into the overall structure of the shape, making it easier to apply formulas and solve problems efficiently.
For certain configurations, the angles are fixed, leading to consistent relationships between the sides. These predictable patterns enable us to solve problems with ease, as the relationships between the angles and sides are well-established and follow geometric principles.
Common Angle-Based Properties
- 30°-60°-90° Triangle:
This triangle has angles of 30°, 60°, and 90°. The ratio of the sides is fixed: the shorter leg is half the hypotenuse, and the longer leg is √3/2 times the hypotenuse.
- 45°-45°-90° Triangle:
In this isosceles right triangle, both legs are of equal length, and the hypotenuse is √2 times the length of either leg. This relationship arises due to the equal angles of 45°.
Angles and Their Effect on Side Lengths
- Impact on Proportions:
The angles directly affect how the sides of the triangle relate to each other. For example, in a 30°-60°-90° triangle, the longer leg is always larger than the shorter leg but smaller than the hypotenuse.
- Predictable Ratios:
When working with triangles that have known angles, the ratios between the legs and the hypotenuse are fixed. This predictability simplifies solving for missing values and helps ensure accurate calculations.
Quick Methods for Solving Right Triangles

When solving for missing sides or angles in a triangle, time-efficient methods can greatly simplify the process. There are several techniques that allow you to quickly determine the unknown values, especially when certain properties or relationships are known. These strategies leverage established geometric rules and formulas to expedite the solution process, minimizing the need for lengthy calculations.
By understanding the specific properties of the triangle’s angles and sides, you can apply various formulas and theorems directly. For example, the use of trigonometric ratios or the Pythagorean theorem can often provide answers in a matter of moments, depending on the available information.
Using the Pythagorean Theorem
- The Basic Formula: The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This formula is extremely useful when two sides are known, and the third side needs to be calculated.
- Example: If the legs of the triangle measure 3 and 4 units, the hypotenuse is found by calculating √(3² + 4²) = 5.
Using Trigonometric Ratios
- Sine, Cosine, and Tangent: When one angle is known (other than the right angle), trigonometric ratios such as sine, cosine, and tangent can help find the remaining sides.
- Example: If the angle is 30° and the hypotenuse measures 10 units, you can calculate the opposite side by using sin(30°) = opposite/hypotenuse. This gives opposite = 10 × sin(30°) = 5.
Practice Problems for Mastering Triangle Concepts
To truly understand the relationships between the sides and angles of a triangle, consistent practice is essential. Working through a variety of problems allows you to solidify key concepts, improve problem-solving skills, and gain confidence. These exercises help in applying different formulas, theorems, and properties to real-world situations, reinforcing the fundamental ideas behind geometric principles.
By regularly practicing these challenges, you can identify the most efficient methods for finding unknown values, whether it’s through algebraic manipulation, trigonometric ratios, or geometric reasoning.
Problem 1: Find the Missing Side Using the Pythagorean Theorem
A triangle has legs of length 8 and 15 units. What is the length of the hypotenuse?
- Step 1: Apply the Pythagorean theorem: a² + b² = c².
- Step 2: Calculate: 8² + 15² = c².
- Step 3: Solve for c: 64 + 225 = c² and c = √289 = 17.
Problem 2: Calculate the Angle Using Trigonometry
A triangle has one leg of length 7 and the adjacent side of length 24. Find the angle between the legs.
- Step 1: Use the cosine function: cos(θ) = adjacent/hypotenuse.
- Step 2: Apply the formula: cos(θ) = 7/24.
- Step 3: Use the inverse cosine function: θ = cos⁻¹(7/24).
- Step 4: Calculate: θ ≈ 72.3°.