
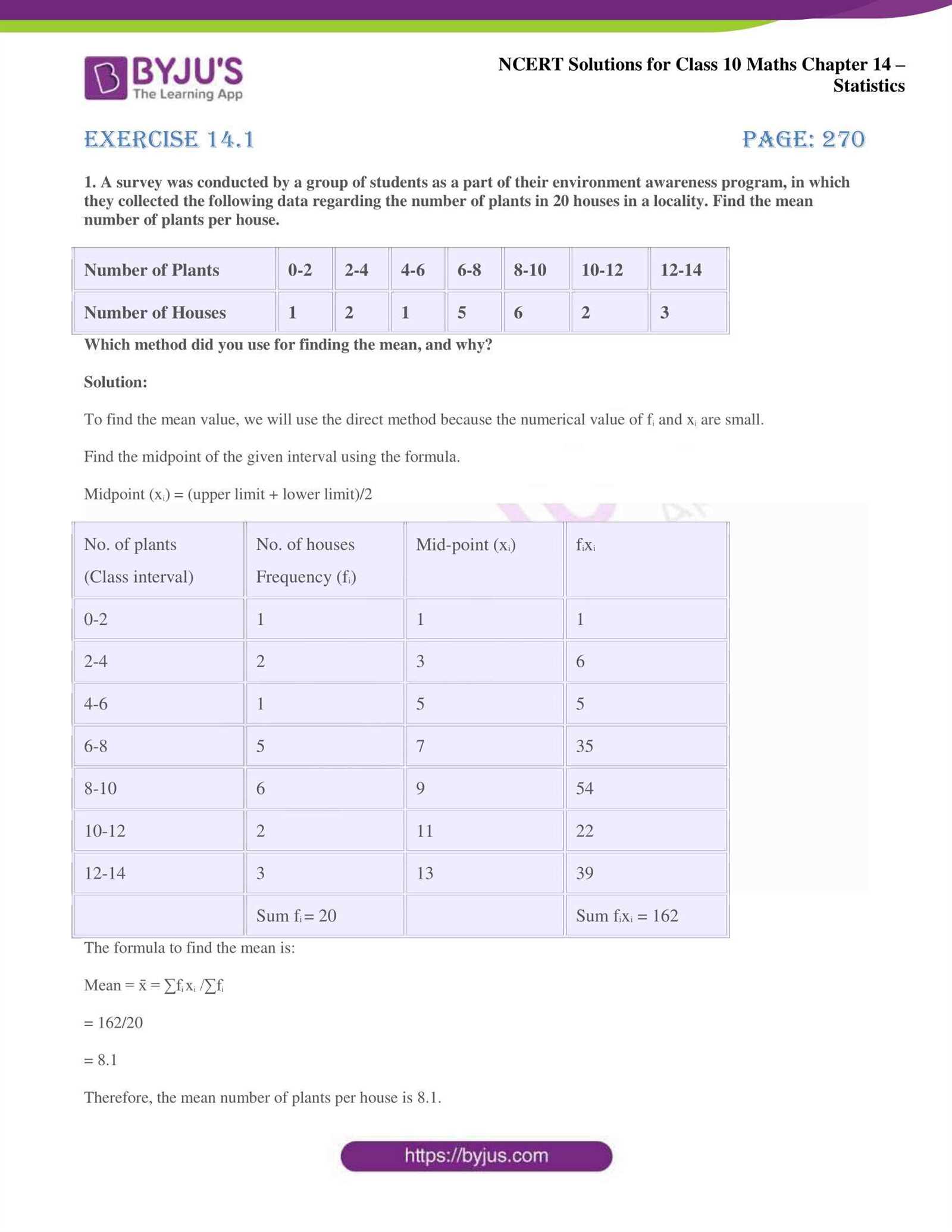
Success in assessments involving numerical analysis and data interpretation requires a solid grasp of core principles and techniques. Being well-prepared for such evaluations involves understanding how to apply various mathematical approaches to real-world situations. In this section, we focus on providing guidance for tackling common problems faced during these types of evaluations.
Preparation is essential for mastering the material, and a strategic approach can help sharpen your skills. Knowing what to expect and how to efficiently manage time is crucial to enhancing your performance. We will explore how specific methodologies can be applied effectively in different scenarios, ensuring a clearer understanding of the subject matter.
Through detailed practice, reviewing various types of problems, and refining your analytical skills, you will feel more confident during your assessment. By focusing on key areas, you will be able to identify patterns and trends that are vital for accurate conclusions. This approach is designed to help you not only perform well but also build a deeper comprehension of the concepts involved.
Key Concepts in Data Analysis
Understanding the fundamentals of numerical analysis is crucial for interpreting results and making informed decisions. This section highlights essential principles that serve as the foundation for evaluating data and drawing conclusions from various experiments and surveys. Mastery of these ideas will not only improve your problem-solving abilities but also give you a clearer perspective on complex tasks.
Fundamental Principles
One of the most important concepts involves identifying the type of data being analyzed and choosing the appropriate methods for processing it. Whether dealing with averages, proportions, or distributions, recognizing the underlying structure of the information helps guide the correct approach. Additionally, knowing how to calculate variances, standard deviations, and other relevant metrics is fundamental for drawing reliable conclusions from the dataset.
Understanding Relationships Between Variables
Correlation and regression are key tools for understanding how variables interact with each other. Recognizing patterns and predicting outcomes based on the relationships between different data points can significantly impact decision-making. It’s important to distinguish between causality and correlation, as confusing the two can lead to incorrect assumptions and conclusions.
Confidence intervals and significance tests provide additional layers of insight into the precision and reliability of data estimates. These concepts help assess whether observed trends are likely to be meaningful or if they could have occurred by chance, offering more certainty in the analysis process.
Essential Formulas for Data Analysis Tests
In any assessment involving numerical interpretation, it is critical to have a solid understanding of the formulas used to calculate key values. These mathematical tools serve as the foundation for solving problems related to data interpretation, hypothesis testing, and predictive analysis. Familiarity with the most commonly used formulas can significantly improve performance in such evaluations.
| Formula | Description |
|---|---|
| Mean = (ΣX) / N | Calculates the average value of a dataset, where ΣX is the sum of all data points and N is the total number of observations. |
| Variance = (Σ(X – μ)²) / N | Measures the spread of data points around the mean, where μ is the mean value and X is each individual data point. |
| Standard Deviation = √Variance | Represents the average distance between each data point and the mean, offering insight into the data’s variability. |
| P-value = Probability of observing the test statistic | Indicates the likelihood of obtaining the observed result if the null hypothesis is true, helping assess the significance of findings. |
| Confidence Interval = Mean ± (Z * Standard Error) | Estimates the range within which the true population mean lies, with a certain level of confidence. |
Mastery of these formulas is essential for quick and accurate calculations during evaluations. A strong grasp of these principles ensures a more systematic approach to solving complex problems involving data interpretation and hypothesis testing.
Common Mistakes in Data Analysis Tests
Even experienced individuals can make errors when interpreting numerical data, especially under pressure. Understanding these common pitfalls is essential for improving accuracy and avoiding costly mistakes. By being aware of frequent missteps, you can enhance your problem-solving skills and improve your overall performance during assessments.
Overlooking Assumptions

A key error often made is neglecting the assumptions underlying various analytical methods. Many statistical tools rely on specific conditions, such as normality of the data or equal variances between groups. Failing to check these assumptions before applying certain formulas can lead to incorrect conclusions. Always ensure that the data meet the necessary conditions before proceeding with advanced calculations.
Misinterpreting Correlation and Causality
Another common mistake is confusing correlation with causality. While two variables may show a strong relationship, it does not necessarily mean that one causes the other. Misinterpreting this can lead to faulty decision-making. Always remember that correlation indicates association, not cause-and-effect, unless proven through additional evidence.
Additionally, failing to properly calculate confidence intervals or significance levels can result in overestimating or underestimating the reliability of results. It’s important to fully understand how these measures reflect the uncertainty of data conclusions, rather than assuming perfect accuracy in every case.
Types of Questions in Data Analysis Assessments
Evaluations that focus on numerical interpretation and data processing typically involve a variety of question formats. These can range from simple calculations to more complex problem-solving tasks. Understanding the different types of questions helps in preparing for such tests and mastering the necessary techniques for answering them correctly.
Calculation-Based Questions
One of the most common types of questions requires performing mathematical operations to obtain a specific result. These tasks often involve:
- Calculating averages or means of given datasets
- Determining variance and standard deviation
- Finding confidence intervals or p-values
- Conducting hypothesis tests
These questions test your ability to apply the appropriate formulas and accurately compute the necessary values from raw data.
Interpretation and Application Questions
Another common type assesses your ability to interpret results and apply them to real-world scenarios. These questions often involve:
- Interpreting the significance of statistical results
- Identifying patterns and trends within a dataset
- Understanding the impact of various variables on outcomes
Such questions evaluate your comprehension of data and your ability to draw conclusions based on the analysis. Success in these tasks requires both a solid understanding of theory and the ability to critically assess numerical findings.
How to Interpret Statistical Data
Interpreting numerical data is a critical skill in understanding trends, making decisions, and drawing meaningful conclusions from research findings. The process involves examining patterns, identifying relationships between variables, and making informed judgments based on available information. Proper interpretation allows for a clearer understanding of how data reflects real-world phenomena and can guide further analysis or action.
Understanding Central Tendency Measures

One of the first steps in interpreting data is recognizing the central tendency, which refers to the typical value of a dataset. The three most common measures of central tendency are:
- Mean: The average value of all data points.
- Median: The middle value when data points are ordered.
- Mode: The most frequent value in the dataset.
Each measure provides a different perspective on the data, and understanding when to use each one is key to accurate interpretation.
Evaluating Data Variability
Beyond central tendency, it’s essential to assess the spread or variability of the data. This is often done using:
- Range: The difference between the highest and lowest values.
- Standard Deviation: A measure of how much individual data points differ from the mean.
- Variance: The average squared deviation from the mean.
Assessing variability helps in understanding the consistency of the data and whether certain trends are statistically significant or could be due to chance.
Understanding P-Values in Data Analysis

Interpreting the results of an analysis involves evaluating the strength of evidence against a null hypothesis. The p-value is one of the most important metrics used to assess this strength. It helps determine whether the observed results are statistically significant or if they could have occurred by chance. A lower p-value indicates stronger evidence against the null hypothesis, suggesting that the observed effect is likely real rather than random.
Understanding the threshold for significance is crucial. Typically, a p-value threshold of 0.05 is used, but this can vary depending on the context of the study. The value itself does not provide direct proof of a hypothesis; rather, it reflects the probability of obtaining the observed data if the null hypothesis were true.
| P-Value | Interpretation |
|---|---|
| Strong evidence against the null hypothesis. Results are considered highly significant. | |
| 0.01 to 0.05 | Moderate evidence against the null hypothesis. Results are generally considered significant. |
| 0.05 to 0.1 | Weak evidence against the null hypothesis. Results may be suggestive but not conclusive. |
| >0.1 | Very weak or no evidence against the null hypothesis. Results are typically considered not significant. |
While the p-value is a useful tool for hypothesis testing, it is important to consider it alongside other factors, such as the size of the effect, the context of the study, and the practical significance of the findings.
Types of Research Designs in Data Analysis
When conducting studies to explore relationships, test hypotheses, or validate theories, the design of the research plays a crucial role in determining the validity and reliability of the results. Different designs allow researchers to approach questions from various angles and help ensure that the findings are meaningful and applicable. Understanding the strengths and limitations of each approach is vital for selecting the best method to address a particular research problem.
Observational Designs
In observational studies, researchers do not manipulate the variables but instead observe and analyze the relationships between them as they naturally occur. These studies are often used when it is not feasible or ethical to conduct experiments. Key types of observational designs include:
- Cohort Studies: Groups of individuals are followed over time to observe outcomes based on certain characteristics or exposures.
- Case-Control Studies: Compares individuals with a specific condition to those without it to identify potential risk factors.
- Cross-Sectional Studies: A snapshot of data collected at one point in time to examine relationships between variables.
Experimental Designs
Experimental designs involve the active manipulation of variables to observe their effects on other factors. These studies are considered the gold standard for establishing causal relationships. Common types of experimental designs include:
- Randomized Controlled Trials (RCTs): Participants are randomly assigned to treatment or control groups to test the effect of an intervention.
- Factorial Designs: A method that evaluates the effects of multiple variables simultaneously, often to observe interactions between them.
Choosing between observational and experimental designs depends on the research objectives, available resources, and ethical considerations. Both have their place in producing robust and reliable findings.
Statistical Tests Used in Medical Studies
In research, various methods are employed to assess data and draw conclusions about the relationships between variables. Statistical tests are tools that help determine if observed patterns or differences are likely due to chance or if they reflect true effects. Different tests are chosen depending on the type of data, the research question, and the assumptions underlying the analysis.
Here are some commonly used tests to evaluate the significance of findings in health-related research:
| Test | Purpose | Use Case |
|---|---|---|
| T-Test | Compares the means of two groups | Used to evaluate if there is a significant difference between two groups (e.g., treatment vs. control) |
| Chi-Square Test | Assesses the relationship between categorical variables | Used to test associations in contingency tables, such as the correlation between a risk factor and a disease outcome |
| ANOVA | Compares means across multiple groups | Used when comparing the effectiveness of more than two treatments or groups |
| Correlation Coefficient | Measures the strength and direction of a linear relationship between two variables | Used to assess how strongly two continuous variables are related, such as age and blood pressure |
| Regression Analysis | Examines the relationship between a dependent variable and one or more independent variables | Used to model outcomes and predict future values, such as predicting a patient’s risk based on multiple factors |
Choosing the correct test depends on the type of data at hand, the number of groups being compared, and the hypothesis being tested. Accurate selection and application of statistical methods ensure that research findings are both valid and reliable.
Improving Time Management for Exam Success
Effective time management is essential for achieving success in any assessment. It involves organizing study time, prioritizing tasks, and staying disciplined in order to maximize productivity and reduce stress. By developing a strategic approach to preparation, individuals can ensure they are well-prepared, confident, and capable of performing at their best under pressure.
One key to success is creating a detailed study schedule that breaks down tasks into manageable chunks. Instead of cramming at the last minute, allocate specific time blocks for each topic, allowing for regular breaks to maintain focus and prevent burnout. Consistency is crucial–making studying a routine rather than a last-minute effort can significantly improve retention and understanding.
Additionally, it’s important to prioritize tasks based on their complexity and relevance. Start with the more challenging areas that require additional attention, and leave the easier topics for later. This approach ensures that energy is focused on the most demanding content, leaving enough time to review and reinforce the material closer to the assessment.
Lastly, practicing under timed conditions can help develop the ability to manage time effectively during the actual assessment. Familiarity with the format, timing, and types of tasks will reduce anxiety and enable more efficient use of time during the actual test.
How to Analyze Data Effectively
Analyzing data involves systematically reviewing and interpreting information to uncover patterns, relationships, and insights that can guide decision-making. It requires not only technical skills but also a strategic approach to ensure that the results are meaningful and applicable. Whether working with numbers, trends, or categories, a clear process is essential to draw accurate conclusions from the available data.
The first step is to organize the data properly. Before diving into analysis, it is crucial to clean and structure the data to remove any errors or inconsistencies that could skew the results. This may involve handling missing values, standardizing formats, or transforming variables into usable forms.
Next, selecting the right tools and methods for analysis is key. Different types of data require different approaches–some might benefit from statistical testing, while others might call for visual representation through graphs or charts. It is important to choose the right technique based on the nature of the data and the questions being asked.
After applying the appropriate methods, interpreting the findings is the next critical step. This includes identifying trends, patterns, and outliers, and assessing the significance of these results. It’s also important to consider the context in which the data was collected and any limitations of the study to avoid drawing unsupported conclusions.
Finally, presenting the analysis in a clear and concise way is essential for communicating the results to others. Effective presentation involves summarizing the key points, explaining the findings in simple terms, and using visual aids like graphs and charts to support the conclusions.
Real-World Applications of Statistical Knowledge
Understanding data and being able to analyze it effectively is a valuable skill in many fields. The ability to interpret numbers and identify trends can drive decision-making, improve processes, and solve real-world problems. Whether in healthcare, business, or social sciences, the application of analytical techniques is crucial for making informed choices that have practical implications.
Here are some common areas where statistical knowledge plays a key role:
- Healthcare and Public Health: Data analysis is used to track disease trends, evaluate treatment effectiveness, and optimize resource allocation. Health professionals rely on this knowledge to improve patient outcomes and manage public health crises.
- Market Research: Companies use data to understand consumer behavior, predict trends, and tailor their products or services to meet customer needs. Statistical tools help businesses make data-driven decisions that lead to better customer satisfaction and increased sales.
- Education: In educational settings, data analysis is used to assess teaching methods, track student performance, and develop targeted interventions to improve learning outcomes. It also helps in evaluating the effectiveness of educational programs and policies.
- Social Sciences: Researchers use statistical methods to analyze survey results, identify patterns in human behavior, and draw conclusions about social phenomena. This knowledge is essential for formulating policies that address societal issues.
- Sports Analytics: Teams and coaches rely on data analysis to improve performance, scout talent, and develop strategies. Statistical models can predict outcomes and help make better decisions in training and game strategies.
In each of these areas, the ability to make sense of complex data enables professionals to make informed choices, improve systems, and predict future trends with a high degree of accuracy. Statistical literacy, therefore, is not just valuable in academic settings but also in everyday decision-making and problem-solving.
Best Study Resources for Medical Statistics
Having access to the right study materials can significantly enhance your understanding and mastery of complex concepts. Whether you prefer textbooks, online platforms, or interactive tools, there are numerous resources available that cater to various learning styles. The key is to choose resources that are well-structured, comprehensive, and aligned with the topics you need to focus on.
Recommended Textbooks and Guides

- Introduction to the Concepts of Data Analysis: A foundational textbook that covers key principles in an accessible manner. It provides step-by-step explanations and practical examples, ideal for beginners.
- Practical Guide to Interpreting Research Data: This book offers insights into data interpretation with real-world case studies, helping readers understand how to apply theory to practice.
- Advanced Methods in Quantitative Analysis: For those looking for a more in-depth exploration of data analysis techniques, this resource dives into complex methods used in various fields.
Online Courses and Platforms

- Khan Academy: Offers free courses that break down complex concepts into digestible lessons. Their interactive exercises help reinforce learning.
- Coursera: Provides a wide range of specialized courses from universities and experts in the field, suitable for both beginners and advanced learners.
- edX: Features comprehensive courses on data analysis and interpretation, offering both free and paid options for learners at all levels.
Interactive Tools and Practice Sites
- Quizlet: A useful platform for testing knowledge and reinforcing key concepts through flashcards and quizzes.
- Desmos: A graphing tool that allows students to visualize data and experiment with different statistical models in real-time.
- R Studio: An interactive environment for statistical computing that helps learners practice coding and data analysis techniques directly.
By utilizing these resources, students can build a solid foundation, improve their analytical skills, and feel more confident in their ability to understand and interpret data effectively.
Practice Questions for Medical Statistics Exams

To prepare effectively for any assessment, practicing with real-world scenarios and problems is essential. Engaging with sample exercises helps reinforce concepts, develop critical thinking, and build confidence. The more varied the practice materials, the better prepared you’ll be to tackle any challenge that comes your way.
Problem-Solving Scenarios
- Scenario 1: Given a dataset on patient recovery rates, identify which factors influence the rate of recovery and determine if any correlations exist.
- Scenario 2: Using a provided sample, calculate the mean, median, and standard deviation, then interpret these values in the context of patient outcomes.
- Scenario 3: Analyze survey results to determine the likelihood of a specific treatment being effective for different age groups. Apply statistical tests to assess significance.
Multiple-Choice Practice

- Question 1: Which of the following is an example of a continuous variable in a health study?
- A) Blood type
- B) Age
- C) Gender
- D) Medication adherence (Yes/No)
- Question 2: What statistical test would you use to compare the means of two independent groups?
- A) Paired t-test
- B) Independent t-test
- C) Chi-square test
- D) ANOVA
- Question 3: If the p-value in a hypothesis test is less than 0.05, what does this suggest?
- A) There is no significant difference between groups
- B) The result is statistically significant
- C) The hypothesis is rejected
- D) The sample size is too small
Practicing with these kinds of scenarios and multiple-choice questions allows you to test your understanding and prepare for a wide range of topics and techniques. Regular practice not only solidifies knowledge but also helps develop the skills necessary to interpret data, draw conclusions, and make informed decisions under pressure.
Tips for Answering Complex Statistical Questions
When faced with challenging tasks involving data analysis, it’s essential to break down the problem into smaller, more manageable parts. By following a structured approach and applying logical steps, you can effectively tackle even the most complex scenarios. Being organized and methodical not only boosts accuracy but also improves your ability to think critically under pressure.
Approach to Problem-Solving
- Read Carefully: Ensure that you fully understand the question and all its components before beginning your work. Take note of what is being asked and any specific conditions given.
- Identify Key Variables: Determine the main variables or data points in the task. This helps direct your analysis and ensures you’re focusing on the correct elements.
- Check for Assumptions: Many problems rely on certain assumptions. Identify these and verify that they align with the data or scenario you’re dealing with.
- Work Step-by-Step: Don’t rush. Approach the problem step by step, breaking down complex formulas or concepts into simpler components.
Common Strategies for Success
- Use Visual Aids: Diagrams, graphs, and tables are often helpful for understanding complex relationships and patterns in data. Visual aids can clarify the information and make it easier to analyze.
- Practice Mental Math: Strengthen your ability to quickly perform calculations in your head. This is especially useful when time is limited or when using a calculator isn’t allowed.
- Check Your Work: Double-check your calculations and logic before finalizing your answers. This helps avoid simple errors that could lead to incorrect conclusions.
- Stay Calm: When confronted with a difficult task, it’s crucial to remain calm. Stress can cloud judgment and lead to mistakes. Take a deep breath, focus, and approach the problem with confidence.
By applying these strategies, you’ll improve your problem-solving skills, reduce the chances of making errors, and increase your efficiency when working with complex tasks. The key to mastering challenging data problems lies in understanding the underlying principles and practicing regularly to enhance your expertise.
Understanding Confidence Intervals in Exams

When interpreting results, it’s important to grasp the concept of ranges that reflect the uncertainty or precision of estimates. These ranges offer insights into the reliability of your findings, showing where the true value is likely to lie based on the sample data. Understanding how to interpret these ranges can significantly impact your ability to analyze results accurately in assessments.
Key Concepts to Keep in Mind
- Range of Values: A confidence range provides a range within which the true population parameter is expected to fall with a certain level of certainty, typically 95% or 99%.
- Level of Confidence: This refers to the probability that the interval contains the true parameter. For example, a 95% confidence level means that 95% of similar intervals will contain the true value.
- Width of the Interval: The width indicates how precise the estimate is. A narrower range suggests more precision, while a wider range indicates more uncertainty.
- Sample Size: Larger sample sizes tend to result in narrower intervals, making the estimate more reliable.
How to Interpret Confidence Intervals
- Confidence Interval Contains Zero: If the interval includes zero, it may suggest no significant difference between groups or no effect. This could indicate that the observed result is due to chance.
- Exclusion of Zero: If the interval does not contain zero, it suggests a statistically significant result, meaning there is a meaningful difference or effect.
- Interpret with Context: While the interval provides important information, always consider the context of the research. A small sample size or high variability can influence the reliability of the interval.
- Consider Practical Significance: Even if the interval is statistically significant, consider whether the difference or effect is large enough to have real-world relevance.
Understanding how to interpret confidence intervals is essential for drawing valid conclusions from data. By paying attention to the level of confidence, the interval’s width, and its relationship to zero, you can make more informed decisions about the significance and reliability of your results.