
In this section, we focus on helping students master important mathematical concepts through structured practice and clear explanations. The content is designed to guide learners step-by-step, providing them with the tools needed to understand and solve various challenges efficiently.
Throughout this guide, you will find solutions and strategies that reinforce the fundamental principles taught in the course. By following the provided examples, students will improve their confidence and skills, ensuring a stronger grasp of the material. The focus is on enhancing comprehension and fostering independent problem-solving abilities.
Detailed explanations and practical tips will help navigate the more complex topics, breaking them down into manageable parts. This approach not only simplifies difficult problems but also encourages a deeper understanding of the underlying concepts.
Grade 4 Problem-Solving Support
This section provides a comprehensive guide to help students tackle key challenges encountered in their recent lessons. By working through the examples provided, learners will gain a clearer understanding of the steps required to solve complex exercises and enhance their problem-solving abilities. Each step is carefully outlined to ensure clarity and reinforce essential skills.
Understanding the Approach
Focusing on logical reasoning and step-by-step solutions, the approach helps students break down complex tasks into manageable components. This method ensures that learners can confidently approach similar problems in the future, applying the same strategies to different scenarios. The key is consistency and practice, which build confidence over time.
Strategies for Success
Practice and review are vital for mastering difficult topics. By revisiting challenging exercises and using practical tips to navigate tricky steps, students will strengthen their ability to think critically. Regular self-assessment and guided exercises are crucial in solidifying the knowledge needed to excel.
Overview of Learning Unit 7

This section provides an in-depth look at the key concepts and topics covered in the recent learning unit. The goal is to guide students through a series of interconnected lessons designed to strengthen their problem-solving skills and deepen their understanding of foundational concepts. Emphasis is placed on building a solid grasp of critical thinking and numerical operations, which will serve as the basis for more complex tasks ahead.
Key Concepts Covered
The focus of this unit is on introducing new strategies for tackling advanced problems. Learners will explore various techniques for breaking down and solving challenging questions, focusing on clarity and precision. Additionally, the unit encourages the development of logical reasoning skills, making it easier for students to approach similar exercises with confidence.
Skills Development
Throughout the unit, students will work on enhancing their ability to analyze problems systematically. By mastering core techniques and practicing regularly, learners will be able to approach more complex scenarios with greater ease. The unit aims to ensure that students are not only able to solve individual problems but also gain a broader understanding of the subject as a whole.
Key Concepts in Unit 7
This section highlights the core ideas and techniques explored in the latest learning unit. The focus is on providing students with the tools they need to navigate more complex exercises while reinforcing previously learned skills. Understanding these foundational concepts is essential for developing a stronger problem-solving mindset and improving overall mathematical proficiency.
Understanding Fractions and Operations
One of the primary concepts in this unit is the manipulation of fractions, including addition, subtraction, and comparison. Students will learn how to work with fractions in various contexts, building their ability to solve problems involving parts of a whole. Mastery of these skills is critical for progressing to more advanced topics that rely on a deep understanding of fractions and their properties.
Exploring Word Problems and Strategies
This unit also emphasizes the importance of reading and interpreting word problems effectively. By developing strategies to break down complex scenarios, students will be able to identify relevant information and apply the right methods to solve each problem. This skill set will improve their ability to approach real-world problems and challenges with confidence.
How to Approach Learning Problems
Solving complex problems requires a systematic approach that breaks down each task into manageable steps. By understanding the structure of each exercise and using effective strategies, students can confidently work through even the most challenging questions. A thoughtful, organized approach helps in identifying key information and applying the correct methods.
To tackle problems efficiently, start by reading the question carefully, identifying what is being asked, and noting any important details. Next, plan a strategy, whether it’s breaking the problem into smaller parts, using diagrams, or applying known formulas. Finally, always double-check the solution to ensure accuracy.
| Step | Action | Tip |
|---|---|---|
| Step 1 | Read the problem carefully | Highlight key information |
| Step 2 | Break down the problem into smaller parts | Focus on one piece at a time |
| Step 3 | Apply the appropriate method or formula | Review past lessons for similar examples |
| Step 4 | Check your work | Revisit the problem to ensure all parts are correct |
Understanding Fractions in Unit 7
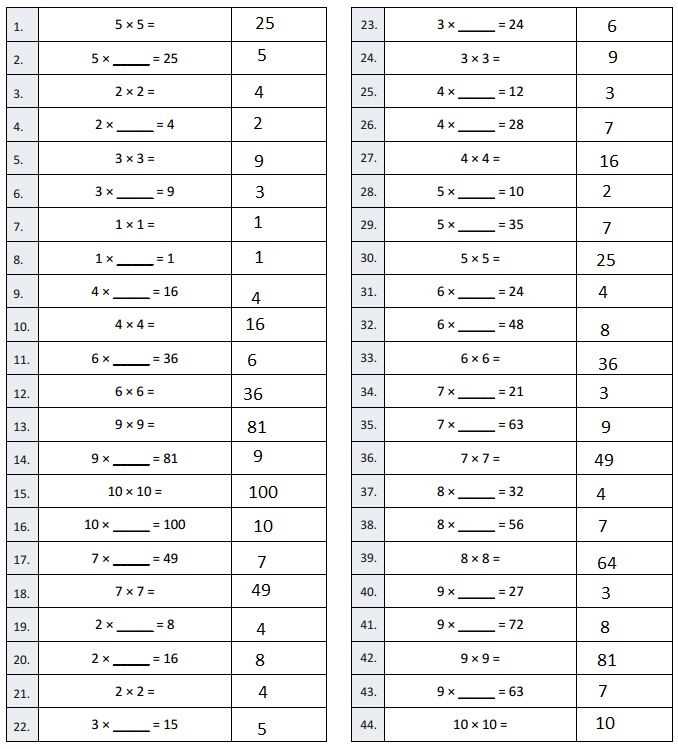
Fractions play a central role in this learning unit, offering students the opportunity to deepen their understanding of parts of a whole. The concept of fractions is vital for solving a wide variety of problems, from simple division to more complex operations. Mastering fractions allows students to confidently tackle tasks that involve splitting, comparing, and manipulating numbers in different ways.
In this section, we focus on the key aspects of working with fractions, from understanding their basic structure to learning how to perform calculations with them. Students will also explore how fractions are used in real-world contexts, reinforcing the importance of this concept in everyday situations.
Key Concepts of Fractions
- Numerator and Denominator: The top number (numerator) represents the number of parts being considered, while the bottom number (denominator) indicates how many equal parts the whole is divided into.
- Equivalent Fractions: Fractions that represent the same value, even though they may look different (e.g., 1/2 = 2/4).
- Comparing Fractions: Understanding how to compare fractions with the same or different denominators by finding a common denominator or converting them to decimals.
- Adding and Subtracting Fractions: Learning how to add and subtract fractions with like and unlike denominators, which involves finding common denominators or converting fractions.
Practical Tips for Working with Fractions
- Always Simplify: When you get an answer, make sure to simplify the fraction if possible to its lowest terms.
- Find Common Denominators: For addition or subtraction, it is crucial to get the same denominator to make calculations easier.
- Use Visuals: Drawing pictures or using fraction bars can help you better understand the relationship between different fractions.
- Practice with Real-Life Examples: Use everyday situations, like dividing a pizza, to understand the concept of fractions.
Common Mistakes and How to Avoid Them
As students progress through their learning journey, it’s natural to encounter challenges and make mistakes. Understanding where these errors occur and learning how to avoid them is crucial for improving accuracy and efficiency. In this section, we will highlight some of the most common mistakes made during problem-solving and offer practical strategies to prevent them.
Frequent Mistakes
- Misinterpreting the Question: Often, students rush through the problem without fully understanding what is being asked. It’s essential to read each question carefully and underline key information.
- Incorrectly Handling Fractions: A common mistake is adding or subtracting fractions with different denominators without first finding a common denominator. This step is crucial for accurate results.
- Forgetting to Simplify: After performing operations with fractions, students sometimes forget to simplify the result to its lowest terms, leading to incorrect or incomplete answers.
- Not Checking Work: Rushing through problems can lead to careless errors. Always take the time to review each step before finalizing an answer.
Tips for Avoiding Mistakes
- Slow Down: Take your time to understand the problem. Break it down into smaller parts and approach it step by step.
- Review the Steps: After completing a problem, double-check your work for any possible mistakes, especially in calculations and fractions.
- Practice Regularly: The more practice you get, the more familiar you will become with the process, reducing the chances of making errors.
- Ask for Help: If you’re unsure about a step, don’t hesitate to ask a teacher or peer for clarification to avoid making the same mistake repeatedly.
Detailed Solution Guide for Unit 7
This section offers a step-by-step breakdown of the solutions to the problems covered in the recent unit. By walking through each example in detail, students will gain a deeper understanding of the strategies and processes required to arrive at the correct answer. The goal is to demystify the problem-solving process and provide clear explanations for each step involved.
Step-by-Step Solutions
The key to solving complex problems is breaking them down into smaller, manageable steps. In this guide, we will demonstrate how to approach each problem, highlighting the methods used to simplify calculations and arrive at the correct results. Whether it’s adding fractions, solving word problems, or comparing values, following the outlined steps will ensure accuracy and clarity.
Example Problem Breakdown
Problem: Add the fractions 3/8 and 5/8.
Solution: Since the denominators are the same, simply add the numerators together: 3 + 5 = 8. The denominator remains unchanged, so the result is 8/8, which simplifies to 1.
Tip: Always check if the fractions have the same denominator before proceeding with the addition or subtraction. If not, find a common denominator first.
Practice Questions for Mastery
To truly master any concept, consistent practice is essential. This section provides a series of questions designed to reinforce the skills learned and help solidify your understanding. By working through these problems, students can gain confidence and improve their problem-solving abilities. Each question is carefully crafted to challenge different aspects of the topic and encourage critical thinking.
As you approach each question, take your time to think through the process, use the strategies you’ve learned, and apply them step by step. Practice not only helps you identify areas of strength but also reveals areas that may need further review.
How Unit 7 Relates to Other Topics
Understanding how different concepts connect can provide a deeper understanding of the subject as a whole. In this section, we explore how the material covered in Unit 7 builds upon prior knowledge and prepares students for future topics. The connections made across various lessons help students see the bigger picture and how different mathematical skills are intertwined.
Connections to Previous Lessons
- Fractions and Division: The work with fractions in this unit connects directly to earlier lessons on division, where splitting quantities into equal parts is a fundamental concept.
- Adding and Subtracting Fractions: Students previously worked with simple addition and subtraction. In this unit, these skills are applied to fractions, requiring a more advanced understanding of operations.
- Understanding Decimal Notation: The knowledge gained in earlier lessons about place value and whole numbers is crucial for understanding fractions and their relationship to decimals.
Preparation for Future Topics
- Advanced Fraction Operations: Mastering the concepts in this unit lays the foundation for more complex operations with fractions, such as multiplication and division.
- Word Problems and Real-Life Applications: The problem-solving strategies used here will be essential in tackling word problems in future units, where applying mathematical skills to real-world scenarios becomes increasingly important.
- Decimals and Percentages: This unit serves as a stepping stone toward understanding decimals and percentages, which are covered in later units and have many real-life applications.
Tips for Efficient Problem Solving

Effective problem-solving requires both strategic thinking and a methodical approach. By developing efficient techniques, students can solve challenges more quickly and accurately. This section outlines practical tips to enhance problem-solving skills, helping students navigate complex problems with confidence.
1. Understand the Problem: Before jumping into calculations, take a moment to fully understand the question. Identify the key information and what is being asked. This will prevent errors and save time.
2. Break It Down: Divide complex problems into smaller, more manageable steps. This will help you focus on one part at a time, reducing the chance of mistakes.
3. Check Your Work: After solving a problem, always review your steps and final answer. A quick check can often reveal small mistakes before they become bigger issues.
4. Use Visual Aids: Draw diagrams, number lines, or models to visualize the problem. This can help clarify relationships between numbers or concepts, making the solution more apparent.
5. Practice Mental Math: Strengthen your ability to solve problems without relying on paper and pencil. This speeds up simple calculations and enhances your overall mathematical agility.
6. Stay Organized: Keep your work neat and structured. Writing down each step clearly can help you track your thought process and identify where any issues may arise.
By implementing these strategies, you’ll improve your efficiency and develop a deeper understanding of problem-solving techniques.
Resources to Support Learning
To excel in any subject, having access to the right resources is essential. Whether it’s additional practice materials, helpful websites, or interactive tools, these resources can significantly enhance understanding and retention. This section highlights some valuable tools and platforms that can assist students in mastering the concepts covered in recent lessons.
Online Tools and Websites
- Khan Academy: Offers a wide range of video tutorials and practice exercises on various topics. These lessons help reinforce key concepts and provide additional examples to strengthen understanding.
- IXL: Provides targeted practice problems based on specific skills. It adapts to the learner’s ability, ensuring that the challenges are appropriately challenging.
- Math Playground: Features interactive games and puzzles that make learning fun while reinforcing important concepts.
Books and Printable Resources

- Workbooks: There are numerous workbooks available that focus on fundamental skills. These provide extra practice and often include step-by-step explanations to help students grasp each topic.
- Flashcards: Using flashcards is a great way to memorize key facts and reinforce concepts. Digital flashcards can be found online, or you can create your own for specific topics.
- Guides and Handouts: Detailed guides and handouts are excellent for reviewing key concepts. These can be used for quick reference or to reinforce learning during study sessions.
Step-by-Step Instructions for Students
Following a clear and organized approach is essential when solving any problem. By breaking down tasks into smaller, manageable steps, students can avoid confusion and achieve better results. In this section, we’ll guide you through a series of steps that will help you effectively tackle complex problems and ensure a thorough understanding of each concept.
Step 1: Read the Problem Carefully
Before starting, make sure to read the problem thoroughly. Identify what is being asked and underline the key details. This will help you focus on the most important information and avoid overlooking essential parts of the problem.
Step 2: Identify What You Need to Find
Clarify what the question is asking you to find. Whether it’s a specific number, a relationship, or a concept, knowing exactly what is required will guide you toward the right solution.
Step 3: Plan Your Approach
Think about the strategies and tools you need to solve the problem. Will you need to use a number line, diagrams, or equations? Planning your approach will help you stay organized and focused throughout the process.
Step 4: Solve the Problem
Using the methods you’ve planned, start solving the problem step by step. Keep track of each step to avoid making mistakes, and don’t hesitate to ask for help if you get stuck.
Step 5: Check Your Work
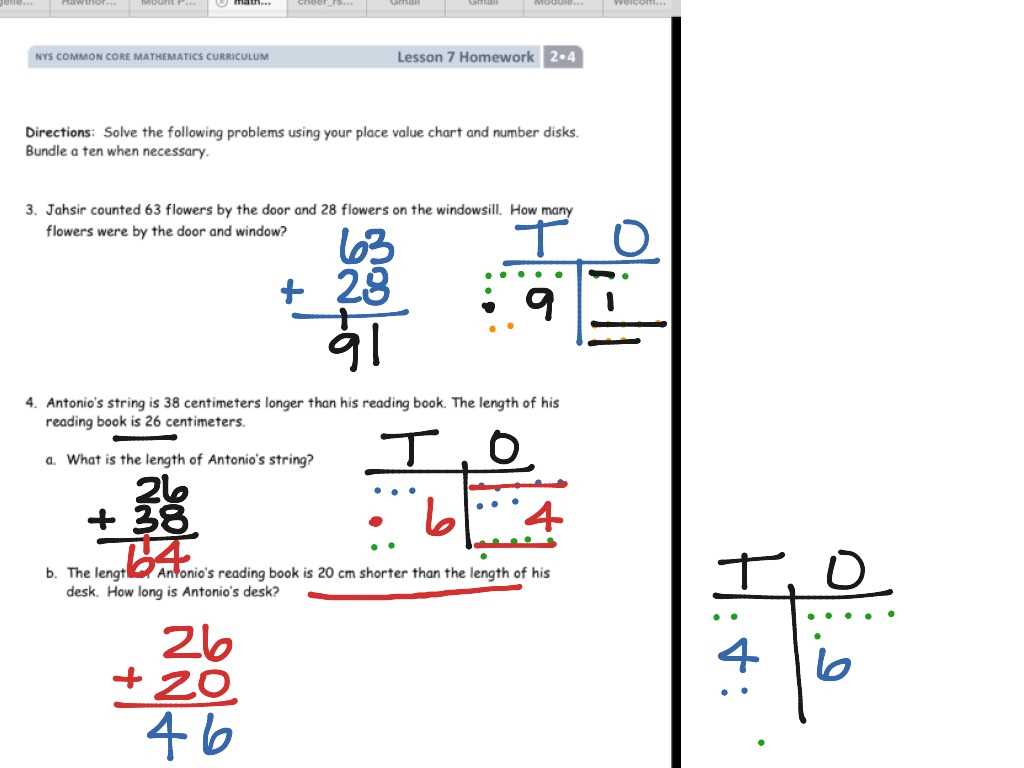
After you’ve reached a solution, go over your steps again. Verify that your calculations are correct and that your answer makes sense in the context of the problem. This is an important step in ensuring the accuracy of your solution.
Reviewing Core Skills from Module 7
Mastering fundamental concepts is essential for building a solid foundation in any subject. By revisiting key skills, students can reinforce their understanding and ensure they are well-prepared for more advanced topics. This section highlights the core abilities from the recent lessons, offering a chance to review and strengthen your grasp of important concepts.
Understanding Fractions and Their Operations
One of the primary skills developed in this section is working with fractions. It’s important to understand how to compare, add, subtract, and multiply fractions. These operations are foundational and appear in a variety of real-life contexts, so practicing them is crucial for long-term success.
Applying Word Problems Effectively
Solving word problems requires careful reading and translating written information into mathematical operations. This skill is vital for approaching real-world situations where problems may not always be presented in a straightforward mathematical form. Revisit strategies for breaking down complex problems into simpler parts to enhance your problem-solving abilities.
How to Check Your Answers
Verifying the accuracy of your work is an essential step in problem-solving. It helps ensure that your calculations are correct and that you’ve followed the proper steps. Checking your results can also give you confidence in your understanding of the material. Below are some effective strategies to review your solutions.
1. Revisit the Problem
Before reviewing your solution, take a moment to read the problem again. Pay attention to the key information and the specific question asked. This will help you confirm that you have addressed all parts of the problem.
2. Check Your Calculations
- Go over each step of your work to ensure the operations were performed correctly.
- Look for any miscalculations, such as adding or subtracting incorrectly.
- Double-check your work with a calculator or estimation, if possible.
3. Use a Different Method
If possible, try solving the problem using a different approach to see if you reach the same conclusion. This can help confirm that your solution is correct and that you understand the concepts involved.
4. Validate with Real-World Logic
After completing the problem, think about whether the result makes sense in the context of the real world. For example, if you’re working with measurements, does the result align with expectations? This can often serve as a quick check on the reasonableness of your answer.
Teacher’s Tips for Module 7 Success

Helping students succeed in problem-solving and understanding concepts requires thoughtful strategies and effective guidance. As an educator, you can enhance student learning by providing clear instructions, encouraging active participation, and offering plenty of opportunities for practice. Below are some teacher tips for ensuring students excel in this section.
1. Break Down Concepts into Manageable Steps
Complex problems can be intimidating for students. Break down each concept into smaller, more digestible steps. This approach helps students focus on one piece of the puzzle at a time, reducing anxiety and increasing their ability to solve each part correctly.
2. Use Visual Aids and Examples
Visual aids are invaluable in helping students understand abstract concepts. Use charts, diagrams, and other tools to illustrate key points. Real-world examples also make the content more relatable, which can improve comprehension.
3. Encourage Active Problem Solving

Rather than simply providing the answers, encourage students to solve problems actively. Create an environment where they feel comfortable making mistakes and learning from them. This active engagement reinforces their understanding and helps them retain concepts longer.
4. Regularly Review Key Concepts
Frequent reviews help reinforce knowledge and address any gaps in understanding. Use short quizzes or group discussions to revisit core ideas. This not only solidifies their learning but also builds confidence as they see how much they have mastered.
5. Provide Timely Feedback
Feedback should be constructive and prompt. Offer positive reinforcement when students are on track and guide them gently when they make mistakes. Timely feedback helps students adjust their understanding and keep progressing without feeling discouraged.
6. Foster a Collaborative Learning Environment
Pairing students for group activities or discussions can promote peer learning. Collaboration helps students clarify concepts and learn from one another’s strategies. It also encourages teamwork and communication skills.
7. Stay Patient and Adaptable
Every student learns at a different pace. Be patient and ready to adapt your teaching methods based on individual needs. Some students may need more time or different approaches to fully grasp a concept, so flexibility is key to their success.
Additional Resources for Success
| Resource | Purpose |
|---|---|
| Interactive Learning Tools | Engage students with interactive games and online activities to reinforce learning. |
| Practice Worksheets | Provide additional practice for students to complete at their own pace. |
| Group Study Sessions | Encourage students to study together for collaborative learning and problem-solving. |
By implementing these tips, teachers can create an environment where students feel confident and equipped to master the content, ensuring success for everyone involved.
Interactive Tools for Practicing Math
Interactive tools offer an engaging way to reinforce key concepts and skills. These resources not only help students practice problems but also provide instant feedback, allowing learners to improve at their own pace. By incorporating digital platforms and hands-on tools, educators can create an environment where students feel motivated to explore and solve challenges independently. Below are some popular interactive tools designed to enhance learning and problem-solving skills.
1. Online Problem Solvers
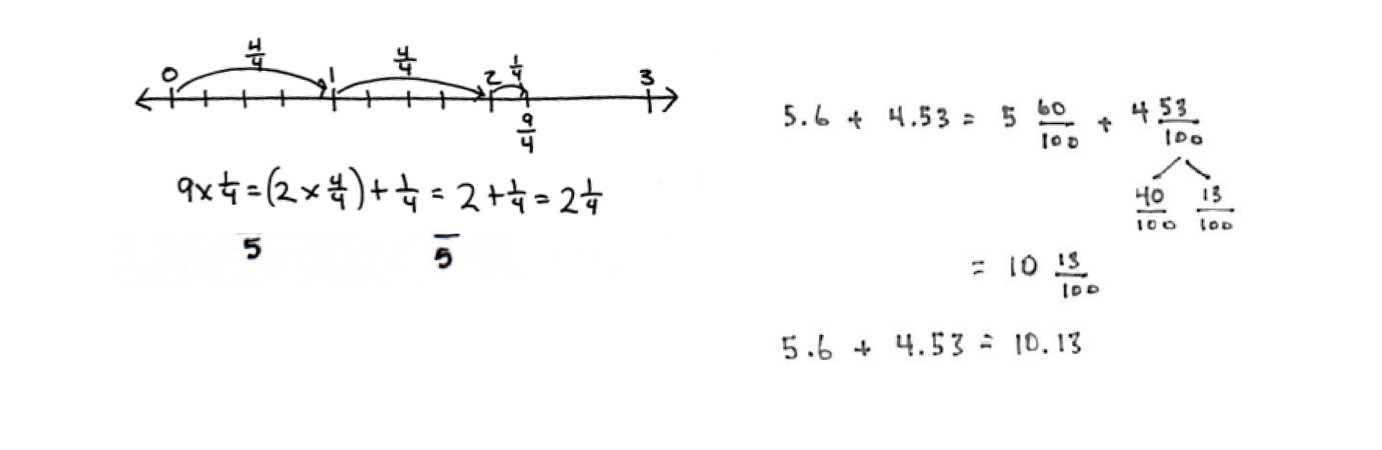
Web-based problem-solving platforms allow students to work through exercises while receiving immediate feedback. These tools often include step-by-step solutions, helping students understand where they may have gone wrong and how to correct their mistakes. Platforms like interactive quizzes and games make practice feel more like play than work, keeping students engaged.
2. Virtual Manipulatives

Virtual manipulatives mimic physical tools like blocks, number lines, and geometric shapes, offering a hands-on experience in a digital format. Students can manipulate objects on their screens to better visualize problems, making abstract concepts more concrete. These tools help deepen understanding, especially for visual learners.
3. Adaptive Learning Software
Adaptive learning programs adjust the difficulty of tasks based on a student’s performance, ensuring that they are continually challenged without feeling overwhelmed. These platforms track progress and adapt in real time, offering personalized learning paths that meet individual needs. This customization helps foster a sense of accomplishment and keeps students engaged.
4. Interactive Whiteboards

Interactive whiteboards allow students to participate in lessons in real time, solving problems directly on the screen. Teachers can use these boards to demonstrate solutions, and students can come up to the board to work through problems themselves. The collaborative nature of these tools helps build a sense of community and encourages active participation.
5. Mobile Apps for Practice
Mobile apps provide flexibility, enabling students to practice whenever and wherever they choose. Many apps offer exercises that range from basic drills to complex problems, allowing for personalized practice. Students can track their progress, receive hints, and set goals, all of which help make learning more self-directed and engaging.
6. Gamified Learning Platforms
Games are an excellent way to make practice fun and interactive. Gamified platforms incorporate problem-solving into game mechanics, allowing students to “level up” as they master new skills. The competitive aspect can motivate students to work harder, while rewards and achievements create a sense of accomplishment.
Using these interactive tools can significantly enhance the learning experience by promoting active engagement, providing immediate feedback, and allowing for personalized learning. When students enjoy the process of practicing, they are more likely to retain information and approach challenges with confidence.
Frequently Asked Questions on Module 7
This section aims to address common questions and provide clarity on various aspects of the content covered. Whether you are a student trying to solve a problem, a teacher looking for guidance, or a parent assisting with homework, these frequently asked questions will help resolve any uncertainties and enhance understanding. Below are some of the most commonly asked queries regarding the concepts in this section.
| Question | Answer |
|---|---|
| What is the best way to approach complex word problems? | Start by carefully reading the problem and identifying key information. Break the problem into smaller, manageable parts and use visuals or diagrams to help with understanding. Don’t hesitate to rewrite the question in simpler terms to ensure clarity. |
| How can I improve my understanding of fractions? | Practicing with real-life examples can help make fractions more tangible. Visual aids like pie charts or fraction bars can provide a better understanding of how fractions work. Additionally, solving progressively more difficult problems will strengthen your skills. |
| What if I make a mistake in a problem? | Don’t be discouraged! Mistakes are an important part of learning. Go back over the steps and try to pinpoint where the error occurred. It can be helpful to work backward or check your calculations to identify the issue. |
| How can I prepare for tests in this section? | Review practice problems regularly, and make sure to go over any concepts you find challenging. Create a study schedule to break up the material into smaller sections. Using interactive tools and engaging in group study sessions can also be helpful. |
| Are there any shortcuts to solving problems faster? | While there are no shortcuts to understanding the material fully, practicing strategies like estimation and rounding can speed up some problems. Mastering the basic concepts and operations will also help you solve problems more efficiently. |
| How do I keep track of my progress? | Use practice tests and quizzes to assess your understanding. Keeping a journal of problems solved and mistakes made is a great way to track your growth. Regular self-assessment and revisiting challenging topics will help improve over time. |
By reviewing these common questions and applying the suggestions, students can gain more confidence in their learning process. It’s important to stay patient and persistent, as understanding takes time and practice.