
In this section, we dive into the fundamental principles that shape the core of natural sciences. Understanding the relationship between forces, motion, and energy is crucial for anyone looking to grasp how the world works at its most basic level. With the right approach, these concepts can be simplified and made easier to comprehend, regardless of complexity.
Effective problem-solving techniques are key to mastering the material. By breaking down complex scenarios into manageable steps, learners can build confidence and gain a clearer understanding of the underlying principles. Through practice and careful attention to detail, students can enhance their ability to tackle any question related to the subject.
The goal is to foster both conceptual understanding and practical application. Whether you’re reviewing theoretical ideas or applying them to real-world problems, the skills you develop here will form a solid foundation for more advanced topics in the future.
Essential Problem-Solving Techniques
In this section, we explore solutions to some of the most fundamental challenges in the study of natural laws. Understanding key principles and applying them to practical scenarios is essential for mastering the material. By working through each problem step by step, it becomes easier to grasp complex ideas and reinforce the core concepts.
Breaking Down Complex Problems
When tackling difficult exercises, it’s important to break them into smaller, more manageable parts. Start by identifying known variables and the goal of the problem. Then, methodically apply relevant formulas and relationships. This approach not only helps avoid confusion but also ensures a clear path to the solution.
Key Principles to Remember

Force, motion, and energy are interconnected, and understanding how they influence one another is crucial. For instance, Newton’s laws provide a framework for understanding how objects respond to various forces. These fundamental ideas are essential for solving even the most challenging questions. Always keep a clear mental picture of how these concepts apply in real-world contexts.
Key Concepts in Chapter 1
This section covers the foundational ideas that form the core of understanding how objects move and interact with their surroundings. These concepts provide a framework for interpreting the physical world, from the simplest actions to the most complex phenomena. By mastering these principles, one can develop the skills needed to approach a variety of challenges effectively.
Understanding the basic relationship between force, motion, and energy is essential for building a solid grasp of the subject. The interplay between these elements determines how objects accelerate, move, and interact under different conditions. Mastery of these key ideas enables students to solve problems and gain deeper insights into the behavior of matter.
In addition, recognizing how measurements and units work together in real-world scenarios is crucial. Whether calculating speed, acceleration, or force, knowing how to apply and convert units ensures accurate results. This understanding also lays the groundwork for more advanced topics in future studies.
Understanding Basic Principles
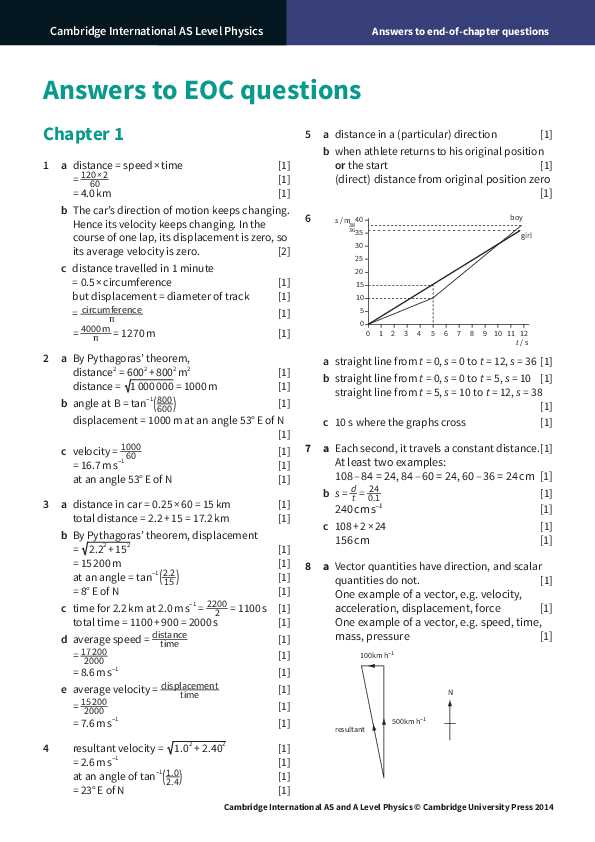
In this section, we explore the fundamental concepts that govern the behavior of matter and energy. These core ideas form the foundation for understanding how objects interact with each other and how forces influence their movement. A clear grasp of these principles is essential for analyzing real-world situations and solving problems accurately.
Forces are at the heart of many physical interactions, whether it’s the pull of gravity, friction, or the force applied to an object. Understanding how forces affect motion helps explain why objects move in certain ways and how we can predict their behavior under different conditions. Additionally, recognizing how energy is transferred and transformed between systems is key to comprehending the workings of the natural world.
Another important aspect is the role of measurement in making accurate predictions. Knowing how to apply the correct units and interpret results allows for a deeper understanding of how objects behave, making it easier to identify patterns and relationships. These principles are not only the basis for solving specific problems but also provide insight into more advanced topics that will be explored in the future.
How to Approach Questions
When facing complex problems, it is important to adopt a systematic approach to break them down into manageable parts. This process helps clarify what is being asked and ensures that all necessary steps are followed for a correct solution. By staying organized and focused, you can effectively solve even the most challenging problems.
Step-by-Step Problem Solving
To approach any problem with confidence, follow these essential steps:
- Read the question carefully – Understand exactly what is being asked before jumping into calculations or assumptions.
- Identify known and unknown variables – Write down the given information and what needs to be found.
- Choose relevant equations – Select the appropriate formulas that relate to the situation.
- Perform calculations – Substitute the known values into the equations and solve for the unknowns.
- Check your work – Review your calculations and reasoning to ensure there are no mistakes.
Tips for Effective Problem Solving

- Visualize the situation – Sketching a diagram can help you understand the problem more clearly.
- Use units consistently – Always double-check that your units match and are properly converted if necessary.
- Practice regularly – The more problems you solve, the more familiar you’ll become with different types of questions.
- Stay organized – Keep your work neat and step-by-step to avoid confusion and mistakes.
Common Mistakes in Problems
Even experienced learners can make mistakes when solving complex problems. These errors often stem from misunderstandings of key concepts, improper application of formulas, or simple calculation mistakes. Identifying and correcting these common pitfalls is essential for improving accuracy and achieving better results.
Frequent Errors in Problem-Solving
Here are some of the most common mistakes to watch out for:
- Misinterpreting the question – Failing to fully understand what the problem is asking can lead to solving the wrong equation or applying the wrong method.
- Not identifying all known values – Overlooking crucial information can prevent the correct formula from being used or cause confusion in calculations.
- Incorrect use of units – Forgetting to convert or incorrectly applying units can lead to inaccurate answers, even if the calculations are otherwise correct.
- Confusing vector and scalar quantities – Mixing up these two types of quantities can result in errors, especially when dealing with directions and magnitudes.
- Skipping steps in calculations – Rushing through the problem-solving process can cause you to miss important intermediate steps, which can lead to incorrect final results.
How to Avoid These Mistakes
To improve accuracy, keep these tips in mind:
- Read the problem carefully – Take your time to understand the question before jumping into the solution.
- Double-check your work – Review each step of your solution to catch any errors before finalizing your answer.
- Practice with a variety of problems – The more problems you solve, the more familiar you will become with common mistakes and how to avoid them.
- Use diagrams when possible – Visual aids can help clarify concepts and reduce errors in interpretation.
Step-by-Step Solution Guide
Breaking down complex problems into smaller, manageable steps is a powerful approach to finding accurate solutions. By carefully following a structured process, you can ensure that each part of the problem is addressed properly, leading to a clear and correct result. This method reduces the chances of making mistakes and helps you understand the reasoning behind every step.
Follow these essential steps to solve problems effectively:
- Understand the problem – Read the question carefully and make sure you know exactly what is being asked. Identify the key elements that you need to focus on.
- Identify known and unknown values – List all the given data and what you are asked to find. Organizing this information makes the solution process easier.
- Select the correct formula – Based on the given values, choose the formula that best fits the situation. If needed, rearrange the formula to solve for the unknown variable.
- Substitute known values – Insert the known values into the formula. Be careful with units and make sure they match appropriately.
- Calculate the result – Perform the necessary mathematical operations to find the unknown value. Double-check your calculations to avoid errors.
- Verify your solution – Check if the answer makes sense in the context of the problem. Reviewing your solution can help ensure it is reasonable and correct.
By following this step-by-step approach, you can tackle any problem methodically and confidently, increasing your chances of success.
Important Formulas to Remember
Mastering the fundamental equations is essential for solving a wide range of problems. These formulas provide the necessary relationships between key physical quantities, allowing you to calculate unknown values based on known data. Having a strong grasp of these equations will help you solve problems efficiently and accurately.
Here are some of the most important formulas to keep in mind:
| Formula | Description |
|---|---|
| Force (F) = mass (m) × acceleration (a) | This equation defines the relationship between force, mass, and acceleration, known as Newton’s second law. |
| Speed (v) = distance (d) / time (t) | This formula calculates the speed of an object based on the distance it travels and the time it takes. |
| Kinetic Energy (KE) = 1/2 × mass (m) × velocity² (v²) | This equation expresses the kinetic energy of an object in motion. |
| Work (W) = force (F) × distance (d) × cos(θ) | Work is the product of force applied over a distance, with θ being the angle between the force and direction of motion. |
| Potential Energy (PE) = mass (m) × gravity (g) × height (h) | This formula calculates the gravitational potential energy of an object at a certain height above the ground. |
Having these formulas readily available will make problem-solving more straightforward. It’s also important to remember the conditions under which each formula is applied to avoid common errors.
Concepts of Motion Explained Simply

Understanding how objects move is fundamental to many areas of study. Whether it’s the motion of a car on a highway or a ball being thrown, the principles governing movement are essential for explaining how and why things change position over time. These concepts can be broken down into basic ideas that are easy to understand with a little thought and practice.
Types of Motion
There are several types of motion that occur in different situations. The most common types include:
- Linear Motion – This involves objects moving in a straight line, such as a car driving along a road.
- Rotational Motion – This occurs when objects spin or rotate around an axis, like the wheels of a bicycle.
- Projectile Motion – This type of motion happens when an object is thrown or propelled, following a curved path due to gravity.
Key Factors Affecting Motion
Several factors determine how and why an object moves, including:
- Speed – This measures how fast an object is moving, often described as the distance traveled per unit of time.
- Acceleration – This refers to the rate at which an object’s speed or direction changes over time.
- Force – The push or pull that causes an object to move or change its velocity.
By understanding these basic principles, you can predict the behavior of moving objects in various scenarios and apply these concepts to solve real-world problems.
Newton’s Laws and Their Applications
Understanding how objects interact with forces is key to describing their motion. The three laws introduced by Sir Isaac Newton form the foundation for much of classical mechanics, offering a simple yet powerful framework for analyzing motion and forces in various situations. These principles can be applied to everything from everyday experiences to complex engineering challenges.
Each of Newton’s laws explains a different aspect of how forces influence the motion of objects:
- First Law (Law of Inertia) – An object at rest will stay at rest, and an object in motion will stay in motion at a constant velocity unless acted upon by an external force. This law explains why it is hard to start or stop moving a car or why we feel pushed back when an elevator starts.
- Second Law (Law of Acceleration) – The force applied to an object is equal to its mass multiplied by its acceleration (F = ma). This law explains how the acceleration of an object depends on both its mass and the force applied. For example, it explains why a lighter object is easier to push than a heavier one.
- Third Law (Action and Reaction) – For every action, there is an equal and opposite reaction. This is why you push off the ground when jumping or why a rocket launches into space by expelling gas downwards.
These three laws can be seen in action every day, from the motion of vehicles to the way forces act on objects in space. Understanding their applications allows for more accurate predictions and better solutions in real-world scenarios.
Understanding Force and Acceleration

Force and acceleration are fundamental concepts in understanding how objects move. These two elements are closely linked, as the application of force to an object leads to a change in its motion. By exploring how force influences speed and direction, we can gain insight into the dynamics of the physical world around us.
When an external force acts on an object, it causes the object to accelerate. The amount of acceleration depends on the strength of the applied force and the object’s mass. The relationship between force, mass, and acceleration is essential for predicting how objects will move under various conditions.
| Concept | Description |
|---|---|
| Force | An influence that causes an object to change its state of motion or shape. |
| Acceleration | The rate at which an object’s velocity changes over time. |
| Mass | The quantity of matter in an object, affecting how much force is needed to accelerate it. |
| Inertia | The resistance of an object to a change in its motion. |
Graph Interpretation in Physics
Graphs are powerful tools for visualizing data and understanding relationships between variables. They allow us to analyze trends, make predictions, and interpret patterns in motion or other phenomena. By examining the shape and behavior of a graph, we can draw conclusions about how different factors influence each other over time or distance.
Understanding how to read and interpret different types of graphs is essential for grasping the underlying principles of motion, forces, and other dynamic processes. Various graph types represent different kinds of data, and each offers unique insights into the behavior of objects or systems.
- Linear Graphs: Represent a constant rate of change, such as uniform motion.
- Curved Graphs: Indicate non-uniform motion or changing rates, often seen in accelerated motion.
- Horizontal Lines: Show no change in the variable, indicating a state of rest or equilibrium.
- Sloped Lines: Suggest a rate of change, with steeper slopes indicating a greater rate of change.
By analyzing these graphs, one can better understand the interaction between the variables and make informed predictions about future behavior.
Calculating Speed and Velocity
Speed and velocity are two fundamental concepts used to describe motion. While they both involve the rate at which an object changes its position, they differ in how they account for direction. Understanding how to calculate these quantities helps in analyzing the movement of objects in various contexts, from simple linear motion to more complex paths.
Speed Calculation
Speed refers to how fast an object is moving, regardless of its direction. It is a scalar quantity, meaning it only has magnitude. To calculate speed, you can use the formula:
- Speed = Distance / Time
Where distance is the total length covered, and time is the duration of travel.
Velocity Calculation
Velocity, unlike speed, is a vector quantity, meaning it includes both magnitude and direction. It indicates the rate of change of position in a specific direction. To calculate velocity, use the following formula:
- Velocity = Displacement / Time
Where displacement refers to the shortest distance between the starting and ending points, and time is the duration taken for the motion.
Both speed and velocity provide valuable insights into motion, but understanding the difference between them is crucial for accurately describing and analyzing movement.
Vectors and Scalars Explained
In the study of motion and forces, quantities can be categorized into two types: those that have only magnitude and those that have both magnitude and direction. Understanding the distinction between these two categories is crucial for analyzing various physical phenomena and for solving problems related to movement and interaction.
Scalars are quantities that are fully described by a magnitude alone, while vectors are quantities that include both magnitude and direction. The difference between these two types of quantities influences how they are represented and manipulated in calculations.
| Quantity | Definition | Example |
|---|---|---|
| Scalar | A quantity that only has magnitude, with no direction involved. | Temperature, Speed, Mass |
| Vector | A quantity that has both magnitude and direction. | Displacement, Velocity, Force |
Understanding these fundamental distinctions allows for more accurate descriptions of the physical world and helps in the proper application of mathematical principles in various contexts.
Physics Questions You Should Know

When studying the fundamental principles of motion and energy, there are several key questions that help build a deeper understanding of how the world around us operates. These questions focus on the core concepts that drive many physical processes and help explain how objects move, interact, and change over time.
By reflecting on these essential questions, you can gain a better grasp of the forces at play in different scenarios and develop the skills needed to analyze complex problems. Below are a few critical inquiries to consider:
- What is the relationship between force and motion? Understanding how force influences the movement of objects is crucial to describing how things behave in different situations.
- How does energy transfer from one object to another? This question touches on the principles of energy conservation and transformation, which are fundamental to all processes in nature.
- How does the mass of an object affect its motion? The mass of an object plays a key role in determining how it responds to external forces.
- What factors determine the speed and direction of an object? Analyzing the combination of forces, velocity, and acceleration helps explain how objects move in space.
By understanding the answers to these questions, you will be better equipped to make predictions about the physical world and solve problems that involve motion, forces, and energy.
Tips for Effective Studying

Mastering the concepts of motion, energy, and forces requires a focused and strategic approach. To excel in understanding these topics, it’s essential to use methods that enhance comprehension and retention. A well-structured study routine combined with active problem-solving can significantly improve learning outcomes.
Start by breaking down complex topics into smaller, more manageable sections. Take time to understand the core principles before moving on to more advanced material. Practice regularly with a variety of problems to reinforce your understanding and identify areas for improvement. Additionally, creating summary notes and visual aids such as diagrams can help make abstract concepts more tangible.
Consistent review and active engagement with the material, such as discussing concepts with peers or teaching them to others, will deepen your grasp and make the learning process more effective.