When preparing for roles that require strong analytical thinking, understanding how to approach complex data challenges is essential. Mastery of core mathematical concepts and their practical applications is key to solving real-world problems. Employers often assess candidates on their ability to navigate various data-driven scenarios, testing both theoretical knowledge and practical problem-solving skills.
Successfully tackling these problems during a discussion demands clarity in explaining methods, as well as a deep understanding of techniques. Being able to demonstrate proficiency with key mathematical principles is an important factor in showcasing one’s expertise. From basic concepts to advanced techniques, candidates should be prepared to articulate their approach to solving intricate challenges.
Through this section, we aim to equip you with the essential tools to handle the most common scenarios you may encounter, offering clear explanations and practical tips to succeed. Mastering these topics will not only help you stand out but also ensure you’re ready for the toughest challenges in analytical roles.
Probability and Statistics Interview Questions
In many job roles, employers seek candidates who can effectively solve analytical problems and explain their approach to data challenges. The ability to demonstrate a strong grasp of mathematical techniques, alongside real-world applications, is often tested through practical scenarios. Understanding how to articulate the steps and reasoning behind solving complex issues is a key part of the selection process.
Common Topics Explored in Analytical Discussions
Candidates are frequently asked to explain fundamental concepts, such as the differences between various models or how to choose the appropriate method for specific data sets. These discussions often cover a wide range of subjects, from fundamental principles to more advanced problem-solving techniques. It is important to be well-versed in core techniques and be able to break down concepts clearly and concisely.
Challenging Problems and Practical Applications
Beyond theory, employers may present real-world scenarios to evaluate how well you apply your knowledge to solve practical challenges. These problems often involve making decisions based on incomplete or complex data. Strong candidates demonstrate not only technical knowledge but also the ability to make logical assumptions and provide clear, reasoned solutions. A successful response should focus on the reasoning behind each step, making sure to justify decisions made throughout the process.
Key Concepts in Probability You Must Know
Mastering the essential principles of this field is crucial for anyone looking to excel in roles that require data-driven decision-making. Understanding the fundamentals provides the foundation for analyzing and interpreting uncertain situations, making sense of random events, and predicting outcomes. These concepts are vital when solving problems that involve chance or uncertainty, allowing you to approach complex situations with confidence.
Fundamental Theorems and Laws
Some core principles, such as the law of large numbers or Bayes’ theorem, are critical for tackling problems in any analytical context. These laws define how random variables behave under certain conditions and guide decision-making when dealing with data that isn’t deterministic. A solid understanding of these theorems allows for more accurate predictions and better handling of uncertainty in practical applications.
Key Measures and Distributions
Understanding the various distributions and measures is equally important. From normal and binomial to exponential and Poisson distributions, each serves a specific purpose depending on the type of data you’re working with. Being able to select and apply the correct model will enable you to solve problems effectively, whether you’re analyzing trends, testing hypotheses, or predicting future events.
Understanding Random Variables and Distributions
In any analytical role, understanding how data behaves and can be modeled is key to making informed decisions. Random variables are essential tools for representing uncertainty, while distributions define how likely different outcomes are. Grasping these concepts allows you to approach a wide range of problems, from simple predictions to complex data analysis, with clarity and precision.
Random variables are used to represent outcomes that are uncertain, whether discrete or continuous. A discrete variable might represent something like the number of heads in a coin toss, while a continuous one could represent measurements such as height or time. By understanding these variables, you can build models that describe the likelihood of various outcomes.
Common Distributions
Different types of distributions are applied depending on the nature of the random variable. Some of the most common ones include:
| Distribution Type | Use Case |
|---|---|
| Normal Distribution | Used for data that clusters around a mean, such as heights or test scores. |
| Binomial Distribution | Applied in scenarios where there are two possible outcomes, like success or failure. |
| Poisson Distribution | Used for modeling the number of events occurring within a fixed interval, like phone calls at a call center. |
| Exponential Distribution | Common in modeling time between events in a Poisson process, such as the time until a machine failure. |
Each distribution has its own properties that define how data points are spread out. Knowing which distribution to use is crucial for solving problems and making predictions effectively.
Exploring Statistical Inference Methods

When analyzing data, drawing conclusions from a sample to make broader generalizations about a population is crucial. This process is known as statistical inference, and it involves using sample data to estimate population parameters, test hypotheses, and make predictions. Mastering these methods is essential for accurately interpreting data and making informed decisions based on uncertain or incomplete information.
Key Inference Techniques
Statistical inference encompasses several techniques that help analysts make valid conclusions. Two of the most widely used methods are estimation and hypothesis testing. Estimation allows you to calculate values that represent population parameters, such as means or proportions, based on a sample. Hypothesis testing, on the other hand, helps you assess whether observed data supports a specific assumption about the population.
Types of Estimations and Tests
There are various types of estimation and hypothesis tests, each suitable for different situations. Below is a table that outlines some of the most commonly used methods:
| Method | Purpose | When to Use |
|---|---|---|
| Point Estimation | Provides a single value estimate of a population parameter. | When you need a quick estimate of a population value from sample data. |
| Confidence Interval | Offers a range of values within which the population parameter is likely to fall. | When you want to quantify the uncertainty around an estimate. |
| Hypothesis Testing | Assesses whether a hypothesis about a population parameter is supported by the data. | When testing assumptions, like comparing group means or proportions. |
| Chi-Square Test | Used to determine if there is a significant difference between expected and observed frequencies. | When analyzing categorical data to check for associations. |
Understanding these techniques allows you to effectively analyze sample data and make data-driven decisions. By choosing the correct inference method, you can ensure that your conclusions are both reliable and meaningful.
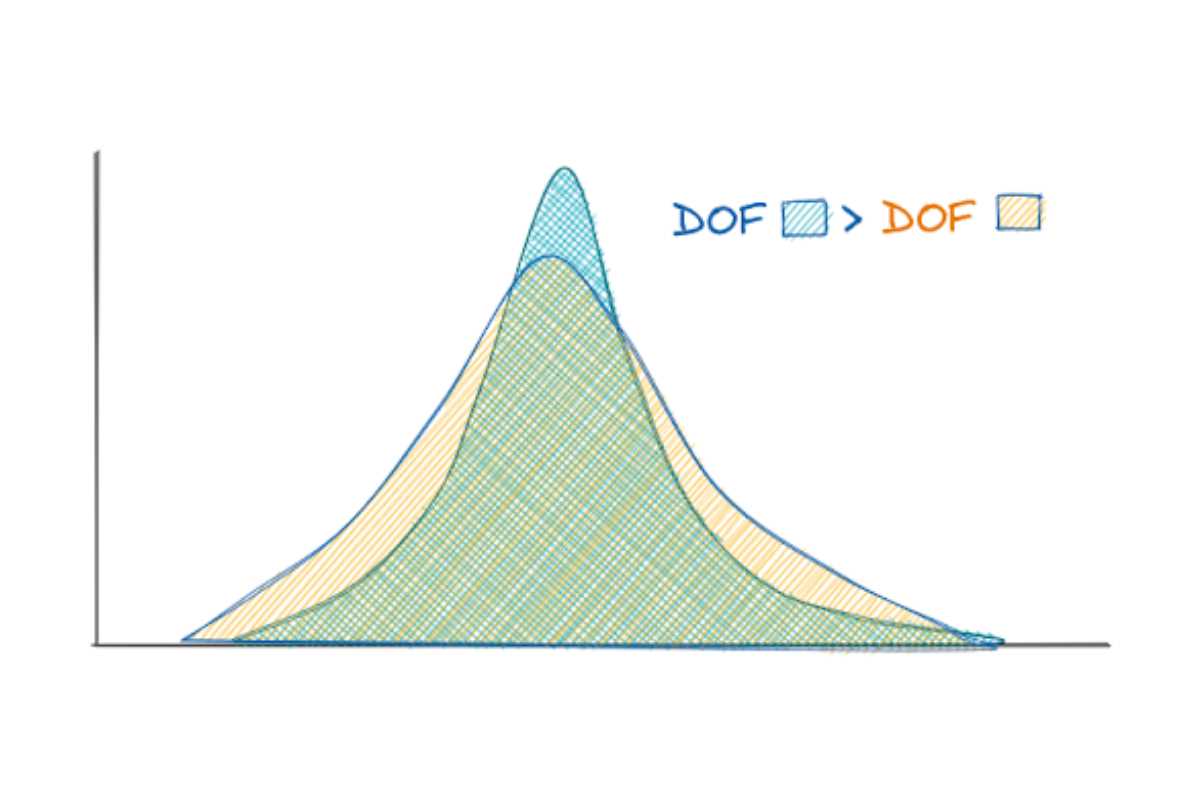
Common Probability Theorems Explained
Understanding foundational theorems is essential for tackling complex problems that involve uncertain outcomes. These theorems provide the basis for modeling random events and making predictions about their behavior. Grasping these concepts allows you to build more accurate models and make better-informed decisions, whether you’re analyzing data or conducting experiments.
Key Theorems You Should Know
Several important theorems form the backbone of many analytical methods. Below are a few of the most frequently applied concepts:
- Bayes’ Theorem: This theorem helps calculate the probability of an event based on prior knowledge of related events. It is especially useful in decision-making scenarios where initial probabilities are updated with new evidence.
- Law of Total Probability: This law provides a way to calculate the total probability of an event by considering all possible ways the event could occur, broken down into mutually exclusive cases.
- Law of Large Numbers: This principle states that as the sample size increases, the sample mean will approach the population mean. It’s crucial for understanding how sample data can represent population data over time.
Applying These Theorems in Real Scenarios
In practice, these theorems are used to refine models and solve problems related to uncertainty. For example, Bayes’ Theorem can help in medical testing, where you update the probability of a disease based on new test results. The Law of Large Numbers underpins many sampling methods, ensuring that the larger the sample, the closer it gets to the true population characteristics.
Being familiar with these foundational theorems enables you to tackle a wide range of problems, from basic calculations to more sophisticated analyses in fields like data science, economics, and engineering.
Handling Hypothesis Testing in Interviews
In many technical roles, assessing your ability to test assumptions about data is an important aspect of the evaluation process. Hypothesis testing is a crucial technique used to determine whether there is enough evidence to support a specific claim or theory. Understanding how to approach these problems methodically is key to demonstrating analytical skills during assessments.
Steps to Approach Hypothesis Testing
When you’re presented with a hypothesis testing problem, it’s essential to follow a structured process. Here’s a general guide:
- State the Hypothesis: Clearly define the null hypothesis (typically a statement of no effect or no difference) and the alternative hypothesis (the statement you’re testing for).
- Select the Significance Level: Choose a threshold (often 0.05 or 5%) that defines how much risk you’re willing to accept for making an incorrect decision.
- Choose the Appropriate Test: Depending on the data and the type of hypothesis, select the correct statistical test, such as a t-test, chi-square test, or ANOVA.
- Calculate the Test Statistic: Using the data provided, calculate the statistic that corresponds to the chosen test, such as a t-value or z-score.
- Make a Decision: Compare the calculated test statistic to the critical value or use the p-value to decide whether to reject the null hypothesis.
Common Pitfalls to Avoid
When addressing hypothesis testing scenarios in an evaluation, there are a few mistakes to be aware of:
- Misinterpreting the p-value: It’s important to remember that a p-value represents the probability of observing the data given the null hypothesis, not the probability that the null hypothesis is true.
- Overlooking Assumptions: Every test has underlying assumptions (e.g., normality, independence). Failing to check these can lead to invalid conclusions.
- Not Considering Type I and Type II Errors: Understanding the risk of both false positives (Type I) and false negatives (Type II) is critical when interpreting results.
By following a clear approach and avoiding common mistakes, you can demonstrate your understanding of hypothesis testing and showcase your problem-solving abilities effectively during assessments.
Importance of Descriptive Statistics
When analyzing data, it’s crucial to summarize and organize information in a meaningful way to uncover patterns and trends. Descriptive techniques are designed to provide simple summaries about the sample and the measures of the data, offering a clear overview of what the dataset looks like. These methods make complex data sets easier to understand and provide a foundation for further analysis.
Key Functions of Descriptive Techniques
Descriptive methods are used to present the basic features of the data in a concise form. They help in identifying central tendencies, variability, and distribution patterns, offering insight into the data’s structure. Below are some key functions:
- Summarizing Data: Descriptive techniques allow you to present large datasets in a more understandable form by calculating averages, medians, and modes.
- Identifying Patterns: These methods help in recognizing trends and relationships, such as whether the data is skewed or follows a particular distribution.
- Comparing Groups: Descriptive tools allow for the comparison of different data groups by calculating measures of dispersion and central tendency.
Practical Applications
Descriptive techniques are widely used across various industries, including business, healthcare, and social sciences. For instance, businesses use these methods to summarize customer behavior data, while healthcare professionals use them to interpret patient statistics and clinical trial results. They serve as the first step in making informed decisions, highlighting areas that need attention or further exploration.
By mastering these techniques, you can simplify complex datasets, extract meaningful insights, and lay the groundwork for more advanced analyses.
Interpreting P-values and Confidence Intervals
When analyzing data, understanding the results of hypothesis tests and estimations is critical for drawing accurate conclusions. Two of the most commonly used concepts in this area are p-values and confidence intervals. These tools help assess the significance of findings and quantify uncertainty, providing valuable insights into the reliability of results. Grasping their proper interpretation is essential for making informed decisions based on data.
Understanding P-values
A p-value represents the probability of obtaining an observed result, or one more extreme, assuming the null hypothesis is true. It helps determine whether the evidence against the null hypothesis is strong enough to reject it. In simple terms, a lower p-value indicates stronger evidence against the null hypothesis. However, it is crucial to remember that a p-value alone does not prove a hypothesis, but rather suggests how consistent the data is with the hypothesis.
- Common Thresholds: A p-value less than 0.05 typically indicates strong evidence against the null hypothesis, while values greater than 0.05 suggest weak evidence for rejection.
- Misinterpretation to Avoid: A p-value does not tell you the probability that the null hypothesis is true. It only measures the likelihood of obtaining the data assuming the null hypothesis holds.
Interpreting Confidence Intervals
A confidence interval (CI) provides a range of values that is likely to contain the population parameter of interest, given a certain level of confidence. For example, a 95% confidence interval suggests that if you were to repeat the sampling process many times, 95% of the intervals would contain the true parameter value. This tool helps quantify the uncertainty around an estimate, offering more information than a single point estimate.
- Wide vs. Narrow Intervals: A narrow interval suggests more precise estimates, while a wide interval reflects greater uncertainty.
- Overlap of Intervals: If two confidence intervals overlap, it indicates that the difference between the groups or conditions might not be significant.
Both p-values and confidence intervals are integral to data analysis, offering insights into the strength and reliability of your results. By understanding how to interpret these tools correctly, you can make more informed decisions and avoid common pitfalls in data-driven conclusions.
Types of Probability Distributions to Study
When analyzing random events, understanding the different models used to represent how outcomes are distributed is essential. These models help quantify the likelihood of various outcomes and offer insights into patterns within the data. By studying the different types of distributions, you can better assess the underlying behavior of variables and make more informed predictions.
Common Distribution Models
There are several key distribution models that are frequently encountered across various fields of study. Below are some of the most important ones to familiarize yourself with:
- Normal Distribution: Often referred to as the bell curve, this distribution is symmetric and describes many natural phenomena, such as heights or test scores.
- Binomial Distribution: This model is used when there are two possible outcomes (success or failure) over a fixed number of trials, such as flipping a coin.
- Poisson Distribution: Useful for modeling the number of events occurring within a fixed interval of time or space, particularly when these events are rare and independent.
- Exponential Distribution: Often used to model the time between events in a process where the events occur continuously and independently at a constant rate.
- Uniform Distribution: This distribution assumes that all outcomes within a certain range are equally likely, such as drawing a card from a well-shuffled deck.
Why Study These Models?
Each of these models provides a different perspective on how outcomes can be distributed across a population or sample. For example, understanding the normal distribution is crucial for many statistical techniques, as it forms the basis for hypothesis testing and confidence intervals. On the other hand, the binomial distribution is essential when dealing with binary outcomes in a set number of trials, such as product defect rates.
- Applicability in Real-World Scenarios: Each distribution model has specific use cases, such as modeling the lifespan of machinery (exponential) or the number of customers arriving at a store (Poisson).
- Foundation for Advanced Methods: These distributions are foundational for more complex statistical methods, including regression analysis and machine learning algorithms.
By mastering these key distribution models, you’ll be equipped to approach a wide variety of problems with a strong understanding of how data behaves in different contexts.
Common Mistakes in Probability Problems
In the realm of data analysis, making mistakes when working with random events or outcomes is easy. These errors can lead to incorrect conclusions, impacting decision-making and overall understanding of the data. Recognizing common pitfalls is the first step in avoiding them, ensuring that your reasoning and calculations remain accurate and reliable.
Misunderstanding Independent Events
One frequent mistake is failing to correctly identify whether events are independent. When events are independent, the occurrence of one does not affect the probability of the other. Confusing dependent events with independent ones can lead to errors in calculations and incorrect assumptions about the relationship between events.
- Example: Assuming that the outcome of one coin flip affects the next flip, even though each flip is independent.
- Solution: Always check whether the events influence one another before applying the rule for independent events.
Incorrect Application of Conditional Probability
Another common error arises when working with conditional probability. Many people mistakenly apply the general multiplication rule for conditional probabilities, without considering the given conditions that alter the sample space or outcomes. This mistake can result in an incorrect understanding of how likely an event is under specific circumstances.
- Example: Misapplying the multiplication rule in a scenario where the sample space changes due to previous outcomes.
- Solution: Always take into account how previous events may influence the probability of subsequent events and adjust calculations accordingly.
Confusing “Or” and “And” Conditions
The words “or” and “and” have different implications in mathematical contexts. Using them interchangeably is a common error. For example, the probability of event A or event B occurring is different from the probability of both events occurring simultaneously. Understanding the difference between these logical operators is key to making accurate predictions.
- Example: Treating the probability of A or B happening as if it were the same as A and B occurring together.
- Solution: Use the addition rule for “or” events and the multiplication rule for “and” events, keeping in mind how they interact.
By being aware of these common errors, you can refine your approach to solving problems and improve the accuracy of your results. Clear understanding and careful application of key concepts are essential to avoid missteps and to draw the right conclusions from data.
Bayes Theorem and Its Applications
Bayes’ theorem offers a powerful method for updating the likelihood of an event based on new evidence. It allows for the revision of initial assumptions when additional data becomes available. This concept plays a crucial role in various fields, especially in situations where decisions need to be made under uncertainty or where prior knowledge can influence conclusions.
Understanding Bayes’ Theorem
The theorem provides a way to calculate the probability of an event by incorporating prior information and conditional data. It helps in updating the belief about an event’s likelihood when new information is introduced. The general form of the formula is:
Posterior Probability = (Likelihood × Prior Probability) / Evidence
By adjusting the prior probability with new evidence, Bayes’ theorem refines our understanding of a given situation. This process is particularly useful in cases where direct observation of an event is not possible, but other relevant data can guide decision-making.
Practical Applications
One of the most notable uses of Bayes’ theorem is in the field of machine learning, where it is applied to classification problems. By continuously adjusting predictions based on incoming data, models can improve their accuracy over time. Some practical applications include:
- Medical Diagnosis: Determining the likelihood of a patient having a specific condition based on symptoms and prior knowledge of disease prevalence.
- Spam Filtering: Identifying whether an email is spam by considering prior information about common spam characteristics and analyzing new email content.
- Predictive Analytics: Forecasting future trends by updating predictions as new data becomes available, such as predicting stock market movements or consumer behavior.
By applying Bayes’ theorem, analysts can refine predictions and make more informed decisions, even when faced with uncertainty. This makes it an invaluable tool in various domains, including artificial intelligence, medicine, finance, and beyond.
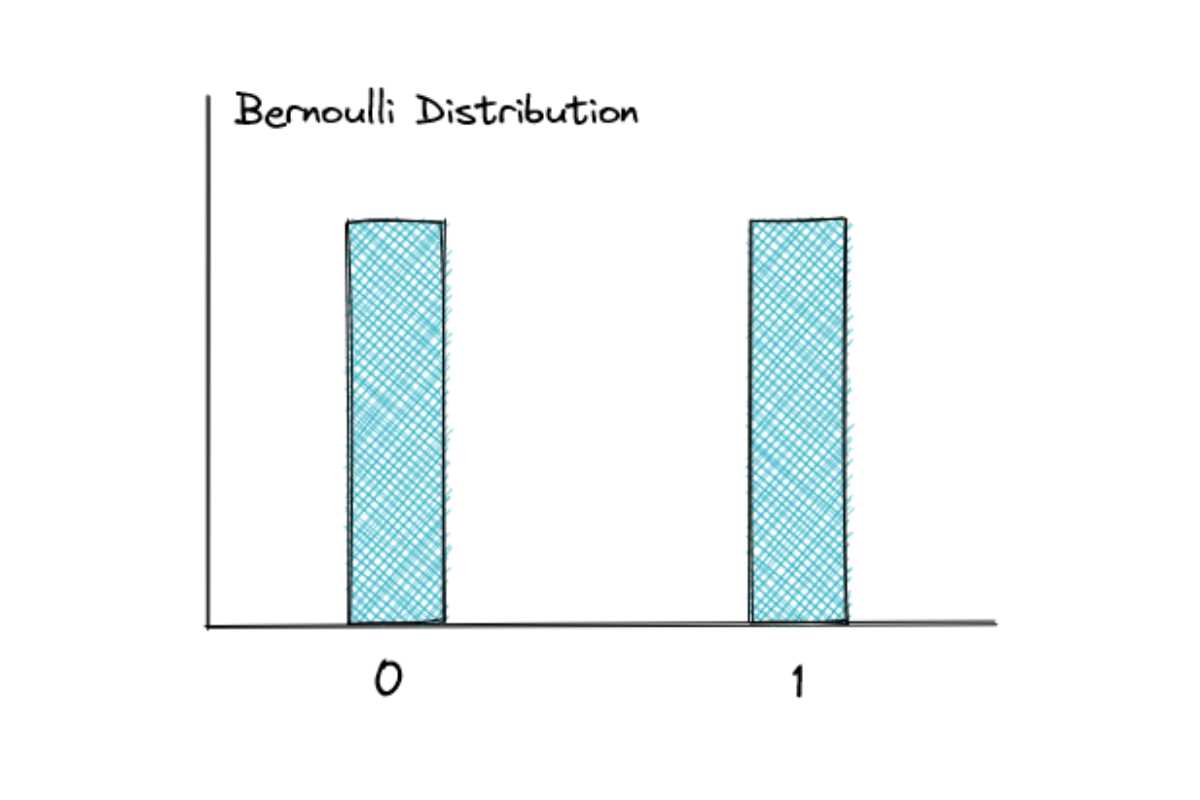
Difference Between Parametric and Non-Parametric Tests
When analyzing data, choosing the right testing method is crucial for drawing valid conclusions. The two main categories of tests used for hypothesis testing are parametric and non-parametric tests. These methods differ in how they approach data, the assumptions they make, and the types of data they are best suited for. Understanding these distinctions helps in selecting the appropriate approach based on the nature of the data and the objectives of the analysis.
Parametric Tests
Parametric tests are based on assumptions about the underlying distribution of the data, typically assuming normality. These tests require the data to meet certain conditions, such as having a known mean and variance. If these assumptions are met, parametric tests are more powerful and provide more precise results.
- Example: T-tests and ANOVA are common parametric tests used to compare means across groups.
- Advantages: These tests are efficient when the assumptions hold true, providing more accurate p-values and confidence intervals.
- Limitations: They cannot be used when the data does not meet the required conditions, such as non-normal distributions or unequal variances.
Non-Parametric Tests
Non-parametric tests do not make any assumptions about the distribution of the data. They are often referred to as “distribution-free” tests. These methods are more flexible and can be used with data that is skewed, ordinal, or non-normal. While they are less powerful than parametric tests when the data meets the assumptions, they are valuable tools when those assumptions cannot be satisfied.
- Example: The Mann-Whitney U test and the Kruskal-Wallis test are non-parametric alternatives to t-tests and ANOVA.
- Advantages: They can handle a wider variety of data types, including ordinal and nominal data, and are robust to outliers.
- Limitations: These tests are less sensitive to small differences in the data and generally require larger sample sizes to detect meaningful effects.
In summary, while parametric tests offer higher power and precision under the right conditions, non-parametric tests provide a useful alternative when the assumptions for parametric methods are not met. Both types of tests are essential tools for data analysis, with each having its own strengths depending on the situation.
Understanding Regression and Correlation
In data analysis, it is crucial to understand the relationship between different variables. Two essential concepts for examining these relationships are regression and correlation. These techniques allow analysts to assess the strength and nature of associations between variables, offering insights that can guide predictions and decision-making. Though related, these concepts serve different purposes and provide distinct insights into data.
Regression Analysis
Regression analysis is used to model the relationship between a dependent variable and one or more independent variables. It helps predict the value of the dependent variable based on the values of the independent variables. This method can provide insights into how changes in the predictors are likely to affect the outcome, making it a powerful tool for forecasting and decision-making.
- Example: Simple linear regression models the relationship between two variables, whereas multiple regression involves more than one predictor.
- Purpose: It is typically used when the goal is to predict a dependent variable or understand the magnitude of change in response to predictors.
- Interpretation: The regression coefficients indicate the strength and direction of the relationship between variables.
Correlation Analysis
Correlation analysis, on the other hand, focuses on measuring the strength and direction of the linear relationship between two variables. It is represented by a correlation coefficient, which ranges from -1 to +1. A correlation coefficient closer to +1 indicates a strong positive relationship, while a value near -1 indicates a strong negative relationship. A value of 0 suggests no linear relationship between the variables.
- Example: Pearson’s correlation coefficient is a common method for calculating the degree of linear association between two variables.
- Purpose: The goal is to determine the strength and direction of the association, rather than predicting or modeling outcomes.
- Limitations: Correlation does not imply causation. It simply measures the association, not the cause-effect relationship.
In summary, while regression is used for prediction and modeling relationships, correlation is concerned with quantifying the strength and direction of relationships. Both are foundational tools in data analysis, each serving a unique purpose in uncovering insights from data.
Important Sampling Techniques for Statisticians
Sampling is a crucial aspect of data analysis, as it helps statisticians draw conclusions about a large population without having to examine every individual element. By selecting a representative subset of data, statisticians can make inferences about the entire population. There are several methods for selecting these subsets, each with its own strengths and applications. Understanding the different sampling techniques is essential for choosing the most appropriate method for a given research problem.
Random Sampling

Random sampling is one of the most fundamental and widely used methods. In this technique, each element in the population has an equal chance of being selected. This ensures that the sample is unbiased and representative of the entire population.
- Advantages: It provides an unbiased estimate of population parameters and reduces selection bias.
- Disadvantages: It can be time-consuming and may not be practical for very large populations.
Stratified Sampling
Stratified sampling involves dividing the population into distinct subgroups, or strata, based on certain characteristics. Then, samples are randomly selected from each stratum. This method is often used when the researcher wants to ensure that certain subgroups are adequately represented in the sample.
- Advantages: It ensures that important subgroups are included, leading to more precise estimates.
- Disadvantages: It requires knowledge of the population structure, which may not always be available.
Systematic Sampling
Systematic sampling involves selecting every nth element from a list or sequence of data points. The starting point is chosen at random, and then the selection proceeds at regular intervals.
- Advantages: It is simpler and faster than random sampling, especially when dealing with large datasets.
- Disadvantages: It may introduce bias if there is a hidden pattern in the data that coincides with the sampling interval.
Cluster Sampling
Cluster sampling is used when the population is geographically dispersed or hard to access. The population is divided into clusters, and then a random sample of clusters is selected. All elements within the chosen clusters are then surveyed or studied.
- Advantages: It is cost-effective and time-efficient, particularly when studying large populations across wide areas.
- Disadvantages: It can introduce bias if the selected clusters are not representative of the population as a whole.
Table of Sampling Techniques
| Sampling Technique | Advantages | Disadvantages |
|---|---|---|
| Random Sampling | Unbiased, representative | Time-consuming, impractical for large populations |
| Stratified Sampling | Precise estimates, ensures subgroup representation | Requires knowledge of population structure |
| Systematic Sampling | Fast, simple | Possible bias if there’s a pattern in the data |
| Cluster Sampling | Cost-effective, time-efficient | Possible bias if clusters are not representative |
By selecting the appropriate technique based on the research goals and data characteristics, statisticians can ensure accurate and reliable results. Each method has its own strengths and weaknesses, so understanding the context in which they are applied is crucial for obtaining valid insights.
Real-World Applications of Probability Theory
Understanding uncertainty is essential in many fields, from finance to healthcare. The study of random events allows professionals to make informed decisions by quantifying risks and predicting outcomes. In various industries, the mathematical tools derived from this theory are applied to improve decision-making, optimize processes, and predict future trends. Below are some common areas where these techniques are crucial in everyday scenarios.
Finance and Risk Management
In the financial world, decision-makers rely on these concepts to assess market behavior, price options, and evaluate investment risks. By modeling the behavior of assets, analysts can predict fluctuations and manage risks associated with investments.
- Applications: Portfolio optimization, risk assessment, pricing derivatives, and calculating insurance premiums.
- Benefits: Helps minimize risk and maximize return in uncertain environments.
Healthcare and Medical Research
Healthcare professionals use these methods to evaluate the likelihood of diseases, predict patient outcomes, and make clinical decisions based on available data. In medical research, these concepts are used to analyze clinical trials, determine the effectiveness of treatments, and estimate the probability of adverse events.
- Applications: Disease modeling, drug effectiveness testing, diagnostic tests, and predicting patient recovery rates.
- Benefits: Provides a way to understand complex biological processes and improve patient care.
Table of Applications
| Field | Application | Benefits |
|---|---|---|
| Finance | Risk assessment, portfolio optimization, derivative pricing | Minimizes risks, maximizes returns |
| Healthcare | Predicting diseases, clinical trials, patient outcomes | Improves decision-making, enhances patient care |
| Engineering | Failure prediction, quality control, process optimization | Reduces defects, increases efficiency |
| Gaming and Sports | Betting odds, performance prediction, game strategies | Informs strategy, estimates game outcomes |
The applications of these concepts extend beyond the areas mentioned here. From machine learning algorithms to marketing strategies, understanding the likelihood of various outcomes is a critical part of many industries. By applying these mathematical tools, professionals across sectors can make data-driven decisions that are based on sound reasoning, even in uncertain conditions.
Tips for Preparing for Statistics Interviews
Preparing for a technical interview in the realm of data analysis or quantitative roles requires a strong foundation in key mathematical principles and the ability to communicate complex ideas clearly. Understanding the core concepts and developing problem-solving skills are essential to performing well. This section outlines practical strategies to excel in these assessments.
1. Review Key Concepts
Start by revisiting the fundamental concepts that are frequently tested in assessments. Focus on areas that are crucial for real-world applications, such as data analysis, hypothesis testing, and model interpretation. Understanding both theoretical knowledge and its practical uses will help you address a wide range of challenges.
- Focus on: Descriptive measures (mean, median, mode), data distributions, regression analysis, hypothesis testing, sampling methods.
- Review: Theoretical background of common techniques, such as t-tests, chi-square tests, ANOVA, and correlation.
2. Practice Problem-Solving
Hands-on practice is essential for building confidence. Solve problems from various resources, including textbooks, online platforms, and past interview examples. Start with easier problems and gradually tackle more complex scenarios. Focus on articulating your thought process and explaining the steps clearly.
- Recommended practice: Work through practice tests and mock problems to familiarize yourself with common question formats.
- Problem types: Expect a mix of theoretical questions, practical problems, and case studies that involve real-life data analysis.
3. Focus on Communication Skills
Effective communication is key during technical evaluations. It’s important not only to solve problems correctly but also to explain your reasoning. Break down complex concepts into digestible parts and make sure to discuss your thought process as you work through a problem. This will demonstrate your depth of understanding and problem-solving abilities.
- Tip: Practice explaining technical concepts to non-experts to ensure you can communicate complex ideas in simple terms.
- Prepare for: Behavioral questions that assess your approach to data challenges, team collaboration, and project management.
4. Understand Tools and Software
Proficiency in data manipulation and analysis tools is often required in technical roles. Ensure you are familiar with widely used software, including statistical packages like R, Python, or SPSS, and have hands-on experience working with real data sets. Employers often look for candidates who can apply mathematical concepts within these tools to derive actionable insights.
- Skills to focus on: Data cleaning, manipulation, visualization, and statistical modeling using appropriate software or programming languages.
- Be prepared: Practice running analysis and interpreting results using real-world data.
In addition to these strategies, consider connecting with professionals in the field through forums or networking events. Getting insights from those who have been through the process can provide valuable tips. With diligent preparation, clear communication, and practical problem-solving skills, you can excel in any technical assessment.