
Successfully navigating the challenges of middle school can be demanding, especially when it comes to mastering essential subjects. Understanding core principles in various topics is crucial for building a strong foundation. This section provides clear, step-by-step guidance to help students strengthen their grasp on critical concepts that will serve them throughout their academic journey.
Developing a solid understanding of fundamental principles is vital for tackling more complex material. By focusing on effective strategies and practical exercises, learners can enhance their skills and boost confidence. With the right approach, even the most challenging subjects can become manageable and rewarding.
Whether it’s solving problems, applying formulas, or mastering specific techniques, this guide offers valuable insights that cater to various learning styles. Each section is designed to provide support and make the learning process smoother and more efficient. By utilizing these tools, students can make steady progress and achieve academic success.
Big Ideas Math 6th Grade Overview
At this level of learning, students are introduced to a variety of essential concepts that will form the basis for more advanced studies in later years. The curriculum focuses on building a deeper understanding of core topics while reinforcing foundational skills that are critical for academic growth. This phase aims to equip students with the tools they need to tackle complex problems in both theory and practical applications.
Key Areas of Focus
The primary subjects covered in this stage include fractions, decimals, ratios, and basic geometry. These topics are essential for developing problem-solving strategies and fostering critical thinking. By exploring these areas in depth, students gain the confidence to approach new material with a clearer understanding and a methodical approach.
Building Problem-Solving Skills
Problem-solving is at the heart of the curriculum, with an emphasis on logical reasoning and critical analysis. Through various exercises, students learn to break down complex problems into manageable steps. Mastery of these skills not only aids in academic success but also prepares learners for real-life scenarios where strategic thinking is essential.
Key Concepts in 6th Grade Math

At this stage of learning, students delve into several important topics that are fundamental for further academic development. The focus shifts to enhancing comprehension of various numerical operations, measurements, and problem-solving techniques. Gaining proficiency in these areas lays the groundwork for future success in more advanced subjects.
Fractions and decimals are essential building blocks, helping students understand parts of a whole and perform operations with numbers less than one. Mastering these concepts is crucial for handling more complex arithmetic tasks later on. Similarly, ratios and proportions provide practical tools for comparing quantities and solving real-life problems.
Geometry introduces students to shapes, their properties, and the relationships between them. Understanding concepts like area, perimeter, and volume is vital for interpreting spatial information accurately. By strengthening skills in these areas, learners not only enhance their mathematical knowledge but also develop a more analytical mindset.
Understanding Problem-Solving Strategies
Effective problem-solving is at the core of academic success. By learning how to approach and break down challenges, students develop valuable skills that extend beyond the classroom. The key to success lies in using structured methods that help organize thoughts and guide actions towards a solution. Mastering these techniques enables learners to tackle even the most complex tasks with confidence and clarity.
One of the most effective strategies is identifying the problem clearly. Before attempting to find a solution, it is crucial to understand the question being asked and what information is provided. Once the problem is clearly defined, the next step is choosing the right approach, whether it involves computation, drawing a diagram, or applying logical reasoning.
Breaking down the steps is another important part of the process. By dividing a complex problem into smaller, more manageable pieces, students can work through each part systematically. This not only simplifies the problem but also helps build confidence as they work through the solution in stages.
Tips for Mastering Math Equations
Mastering equations requires practice, patience, and a strategic approach. By breaking down the process into manageable steps and using effective techniques, students can develop a deeper understanding and gain confidence in solving problems. These skills are not only essential for academic success but also for applying logical thinking in everyday situations.
Understand the Basics
Before jumping into complex problems, it’s important to have a solid grasp of the foundational principles. Knowing the basic operations and how they relate to one another is key to solving more advanced equations. Here are some tips to keep in mind:
- Familiarize yourself with different types of equations (e.g., linear, quadratic, fractions).
- Know how to perform operations such as addition, subtraction, multiplication, and division.
- Understand the use of parentheses and order of operations (PEMDAS).
Step-by-Step Approach

Breaking down the solution process into smaller steps can make even the most challenging equations seem more manageable. Following a structured approach ensures that all parts of the equation are addressed correctly. Here’s how to approach each problem:
- Read the problem carefully and identify what is being asked.
- Isolate variables and move constants to one side of the equation.
- Apply operations step by step to simplify the equation.
- Check your solution by substituting it back into the original equation.
With consistent practice, mastering equations becomes a rewarding and achievable goal. Staying organized and methodical in solving problems is the key to success.
How to Approach Word Problems
Word problems can often seem intimidating, but with the right approach, they can be broken down into manageable steps. The key is to carefully read the problem, identify the relevant information, and apply logical reasoning to find the solution. By following a structured method, students can develop the skills needed to solve these challenges confidently and efficiently.
Step-by-Step Strategy
Here is a simple approach to tackle word problems:
- Read the Problem Carefully: Understand what is being asked. Highlight or underline important information.
- Identify the Given Data: Extract numbers, units, and conditions that are provided in the problem.
- Determine the Unknown: Figure out what you need to solve for.
- Plan Your Approach: Decide on the operations or strategies needed to solve the problem.
- Check Your Solution: Review your calculations to ensure the answer makes sense in the context of the problem.
Using a Table to Organize Information
When dealing with word problems that involve multiple steps or variables, organizing the information in a table can help simplify the process. Here’s an example:
| Given Information | Variable | Solution Strategy |
|---|---|---|
| John has 5 apples. He buys 3 more. | Let x be the total number of apples. | Add the number of apples John had to the apples he bought: x = 5 + 3. |
| Anna has 12 pencils. She gives 4 to her friend. | Let y be the number of pencils Anna has left. | Subtract the number of pencils given away: y = 12 – 4. |
By using a table to organize data, you can easily track what information you have and what steps to take next. This makes complex problems much easier to manage and solve.
Step-by-Step Guide to Fractions
Understanding fractions is a crucial part of mastering basic arithmetic. Fractions represent parts of a whole, and being able to work with them effectively opens the door to solving a wide range of problems. By following a methodical approach, students can develop a solid understanding of how to add, subtract, multiply, and divide fractions with ease.
Breaking Down Fractions
Before working with fractions, it’s important to understand their structure. A fraction consists of two parts:
- Numerator: The top number, which represents how many parts you have.
- Denominator: The bottom number, which represents how many equal parts the whole is divided into.
Steps for Working with Fractions
Here’s a step-by-step guide to help you perform operations with fractions:
- Identifying Equivalent Fractions: Fractions that represent the same value, even though the numbers may be different (e.g., 1/2 = 2/4).
- Adding Fractions: Ensure the denominators are the same before adding the numerators. If the denominators are different, find the least common denominator (LCD).
- Subtracting Fractions: Like addition, subtract fractions only when the denominators are the same. If not, find the LCD and rewrite the fractions accordingly.
- Multiplying Fractions: Multiply the numerators together, then multiply the denominators together. Simplify the result if needed.
- Dividing Fractions: To divide by a fraction, multiply by its reciprocal (flip the second fraction). Then, follow the multiplication steps.
With practice, these steps will become second nature, allowing you to handle fractions with confidence in various math problems.
Decimals and Their Applications in Math
Decimals are an essential part of arithmetic, allowing us to express values that fall between whole numbers. These numbers are used in many real-life situations, from money transactions to measurements. Understanding how to work with decimals is crucial for solving a variety of problems, whether in the classroom or in everyday tasks.
Key Concepts in Decimals
Decimals are based on the place value system, where each digit represents a power of ten. The number is divided into two main parts:
- Whole Number Part: The digits to the left of the decimal point, representing a full value.
- Decimal Part: The digits to the right of the decimal point, representing parts of a whole.
Applications of Decimals
Decimals are used in various fields to make calculations more precise and easier to understand. Here are a few practical examples:
- Currency: Dollars and cents are expressed as decimals (e.g., $5.75 means five dollars and seventy-five cents).
- Measurement: Lengths, weights, and temperatures are often represented with decimals to provide more accuracy (e.g., 12.5 cm, 3.75 kg).
- Time: Decimals are used in time calculations, such as when converting minutes into hours (e.g., 0.5 hours = 30 minutes).
Being comfortable with decimals allows for more efficient problem-solving, whether calculating costs, interpreting data, or performing everyday tasks that require accuracy.
Mastering Ratios and Proportions
Understanding ratios and proportions is key to solving many types of problems, both in the classroom and in real-world scenarios. These concepts allow us to compare quantities and express relationships between different values. Mastering these skills helps in areas such as scaling recipes, creating models, and analyzing data in various fields.
What Are Ratios?
A ratio is a way of comparing two or more quantities. It shows how much of one thing there is compared to another. Ratios can be expressed in several forms:
- Fraction form: e.g., 3/4.
- Colon form: e.g., 3:4.
- Word form: e.g., “3 to 4”.
Understanding Proportions

A proportion is an equation that shows two ratios are equal. In simpler terms, it is a statement that two ratios or fractions are equivalent. Here’s how to solve a proportion:
- Set up the proportion: If you know three values in a proportion, place them in a fraction format, like so: a/b = c/d.
- Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- Solve for the unknown: After cross-multiplying, you’ll have a simple equation that you can solve for the missing value.
By practicing these steps and applying them to various problems, you’ll develop a solid understanding of how to work with ratios and proportions, making complex problems much easier to solve.
Algebra Basics for 6th Graders
Algebra is a branch of mathematics that introduces students to the concept of using symbols and letters to represent numbers and quantities in formulas and equations. By learning algebra, students begin to solve problems where the exact values are unknown, laying the groundwork for more advanced mathematical concepts in the future.
At this stage, understanding the basic principles of algebra is essential. Students work with variables, constants, and expressions to develop the skills necessary to manipulate and solve simple equations. This foundational knowledge helps in solving real-world problems and understanding relationships between quantities.
Key concepts in algebra include:
- Variables: Letters used to represent unknown values in equations.
- Expressions: Combinations of numbers, variables, and operations that represent a value (e.g., 2x + 3).
- Equations: Mathematical statements that show two expressions are equal, often involving solving for a variable (e.g., 2x + 3 = 7).
As students progress in their understanding of algebra, they will become more comfortable with solving equations, simplifying expressions, and using algebraic concepts to solve everyday problems. The key to mastering algebra is practice and recognizing how to translate real-world situations into mathematical expressions and equations.
Geometry: Shapes and Their Properties
Geometry involves the study of various shapes and their characteristics, such as their sizes, angles, and the relationships between their sides. Understanding these properties is essential not only for solving mathematical problems but also for recognizing shapes in the world around us, from architecture to nature. The more we learn about the properties of shapes, the better equipped we are to understand spatial relationships and solve real-world problems effectively.
In geometry, shapes are categorized based on their specific characteristics, such as the number of sides, angles, and symmetry. By exploring these properties, students can begin to see how different shapes relate to one another and how to classify and work with them. Here are some basic shapes and their defining properties:
| Shape | Properties |
|---|---|
| Triangle | 3 sides, 3 angles, the sum of angles is always 180° |
| Square | 4 equal sides, 4 right angles, opposite sides parallel |
| Rectangle | 4 sides, opposite sides equal, 4 right angles |
| Circle | No sides, all points equidistant from the center |
| Polygon | Many sides, classified by the number of sides (e.g., pentagon has 5 sides) |
As students dive deeper into geometry, they learn how to calculate areas, perimeters, and volumes of various shapes. Understanding these fundamental properties forms the basis for solving more complex geometry problems and applying this knowledge in practical ways, such as designing objects or analyzing structures.
Understanding Probability and Statistics
Probability and statistics are fundamental concepts that help us make sense of data and predict future events. These areas of study allow us to analyze trends, understand uncertainty, and make informed decisions based on available information. By mastering these topics, students can better understand the likelihood of various outcomes and how to interpret patterns in data effectively.
Probability: Predicting Outcomes

Probability is the study of the likelihood of an event occurring. It is often expressed as a number between 0 and 1, where 0 means an event will not happen, and 1 means an event is certain. Probability can be used to predict the chance of outcomes in everyday situations, such as flipping a coin or drawing a card from a deck. The basic formula for probability is:
Probability = (Number of favorable outcomes) / (Total number of possible outcomes)
Statistics: Analyzing Data
Statistics involves collecting, organizing, and interpreting data to find patterns or trends. It allows us to summarize information and make decisions based on evidence. Key concepts in statistics include mean, median, mode, and range, all of which help to summarize a data set.
| Term | Definition |
|---|---|
| Mean | The average of a set of numbers, found by adding all values and dividing by the total number of values. |
| Median | The middle value in a data set when the numbers are arranged in ascending or descending order. |
| Mode | The number that appears most frequently in a data set. |
| Range | The difference between the highest and lowest values in a data set. |
By learning both probability and statistics, students gain valuable tools to approach decision-making, problem-solving, and understanding data in everyday life. Whether analyzing survey results, calculating the likelihood of certain events, or interpreting research data, these concepts provide a solid foundation for thinking critically about the world around us.
Improving Mental Math Skills
Strengthening mental calculation abilities is a valuable skill that enhances everyday decision-making and problem-solving. By practicing mental arithmetic, students can improve their ability to perform calculations quickly and accurately without relying on a calculator or paper. This not only boosts confidence but also helps in tackling more complex problems with ease. There are several techniques that can make mental computation more efficient and effective.
Techniques for Faster Calculations
Here are some helpful strategies to improve mental calculation skills:
- Break down complex problems: Instead of solving large problems all at once, divide them into smaller, more manageable parts. This approach makes the calculation easier and faster.
- Use estimation: Estimating values before performing exact calculations helps to quickly gauge an answer. It also allows for a rough answer when precision is not essential.
- Learn number patterns: Recognizing patterns in numbers can speed up calculations. For example, knowing that multiplying by 9 is the same as multiplying by 10 and subtracting the original number helps simplify the process.
- Practice with mental shortcuts: Learn simple shortcuts for addition, subtraction, multiplication, and division. For example, adding in steps (e.g., 25 + 30 = 55, then 55 + 40 = 95) helps break up mental barriers.
Benefits of Regular Practice
Practicing mental calculations regularly leads to better number fluency, sharper focus, and increased speed in problem-solving. Over time, students will become more comfortable solving problems without external tools, making them more confident in various academic and real-world situations.
- Improved accuracy: Regular practice helps reduce errors, allowing for faster and more reliable solutions.
- Better problem-solving skills: As students become more comfortable with numbers, they develop the ability to approach complex problems with greater ease.
- Enhanced cognitive function: Mental calculations help improve memory, concentration, and overall brain function.
Incorporating these practices into daily routines and challenges can significantly enhance mental computation skills, making math both more accessible and enjoyable.
Tools to Help with Homework
Completing assignments efficiently and accurately often requires more than just basic knowledge. Various tools are available that can support students in solving problems, organizing their work, and checking their results. These tools not only provide quick solutions but also offer valuable learning opportunities by reinforcing key concepts. Whether it’s digital apps, websites, or traditional tools, there are plenty of resources that can help boost confidence and improve performance.
Digital Tools and Apps
In today’s digital age, there are many online platforms designed to assist with academic tasks. These tools provide step-by-step explanations, interactive lessons, and instant feedback.
- Online Calculators: Websites like Wolfram Alpha or various mobile apps offer advanced calculators that help solve complex problems instantly. They also often provide detailed solutions, making it easier for students to understand the steps involved.
- Homework Help Websites: Websites such as Khan Academy, Mathway, and IXL offer tutorials, exercises, and personalized feedback. These resources cover a wide range of topics and allow students to practice problems at their own pace.
- Interactive Tools: Programs like GeoGebra provide dynamic geometry and algebra tools. These are great for visual learners who need to see concepts in action to better understand them.
Traditional Tools for Success
In addition to digital tools, traditional resources can also be highly effective for homework assistance. These methods can be used alongside modern apps for even better results.
- Graphing Calculators: A staple in higher-level math, graphing calculators like TI-84 can help students visualize equations, graphs, and solutions. Many students find them invaluable for both homework and exams.
- Reference Books: Textbooks and reference guides are still one of the best ways to understand foundational concepts. They provide clear explanations and examples that help solidify what has been learned.
- Pencil and Paper: Sometimes, the best way to organize thoughts and solve problems is the simplest one. Writing out the steps by hand can help reinforce concepts and improve memory retention.
By using these tools effectively, students can gain better insight into their assignments, develop stronger problem-solving strategies, and work more efficiently. Whether digital or traditional, the right tools can make all the difference in achieving success in any subject.
Common Mistakes and How to Avoid Them
When solving problems, it’s easy to make mistakes that can derail progress. Often, these errors are simple but can lead to confusion and incorrect results. Recognizing common pitfalls and understanding how to avoid them is essential for improving problem-solving skills and achieving better outcomes. Below are some of the most frequent mistakes students make and practical tips on how to prevent them.
Misunderstanding Problem Requirements
One of the most common errors is failing to fully understand what the question is asking. This often happens when students rush through the problem without carefully reading the instructions or identifying key details. To avoid this:
- Read carefully: Always read the problem multiple times to ensure full comprehension.
- Highlight key information: Mark important numbers, words, or phrases that tell you what to do.
- Paraphrase the question: Try rephrasing the question in your own words to ensure you understand the objective.
Skipping Steps or Not Showing Work
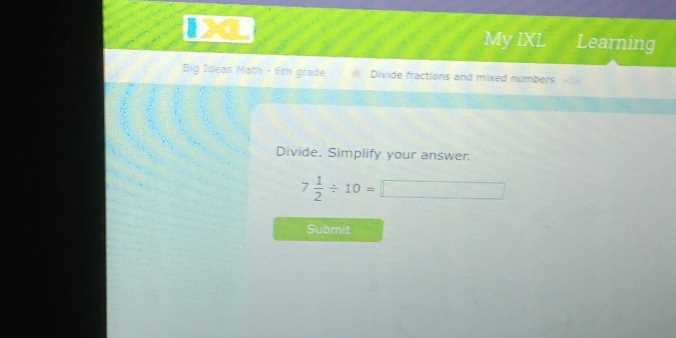
Skipping steps or not showing the work behind each solution is another common mistake. This can lead to confusion, especially when checking answers or identifying where something went wrong. To prevent this:
- Write everything down: Even if you can solve the problem in your head, write out each step to avoid missing important details.
- Break problems into smaller parts: Tackle the problem step by step to ensure you are following the correct process.
- Check your work: After completing a problem, go back and review your steps to make sure you didn’t overlook anything.
Making Calculation Errors
Calculation errors, such as adding or multiplying incorrectly, can happen when students are working too quickly or not double-checking their results. To minimize mistakes in calculations:
- Use tools for assistance: Double-check your calculations using a calculator or by doing them manually a second time.
- Check your work step by step: After solving a part of the problem, pause and ensure that each step was completed correctly before moving on.
- Work slowly and carefully: Take your time when performing calculations, especially when dealing with large numbers or fractions.
Overlooking Units and Conversions

For problems that involve measurements or conversions, students often forget to account for units, which can lead to incorrect answers. To avoid this mistake:
- Always include units: Write the units of measurement alongside your numbers to avoid confusion.
- Convert properly: Make sure to convert units correctly when needed, and double-check conversion factors.
- Ask yourself if units match: Before finalizing your answer, ensure that the units of the input and output are consistent.
Relying Too Much on Memory
Relying solely on memory for formulas or procedures can lead to mistakes, especially when there are complex concepts involved. To reduce errors from memory lapses:
- Write down formulas: Keep a list of important formulas and concepts handy during your work.
- Practice regularly: The more you practice, the more likely it is that formulas and procedures will stick in your mind.
- Understand the logic: Instead of just memorizing, focus on understanding how formulas are derived and
How to Prepare for Tests
Preparing for an assessment involves more than just memorizing formulas or equations. It’s about building a deep understanding of the subject and developing strategies to approach problems effectively. By organizing your study time, practicing regularly, and staying focused, you can improve your ability to perform under pressure and ensure you’re fully prepared for any test.
One of the most important steps in getting ready is creating a study schedule that breaks down the material into manageable chunks. This ensures you can focus on one topic at a time without feeling overwhelmed. Regular practice is key–working through different types of problems will strengthen your skills and boost your confidence. Equally important is reviewing your mistakes so that you can understand where you went wrong and avoid repeating them.
Another helpful strategy is to take practice tests, which simulate real test conditions. This helps you get used to the format and timing, and it also reveals any gaps in your understanding. Finally, staying calm and positive is crucial. A confident mindset, coupled with a good night’s rest before the test, will help you think clearly and perform to the best of your ability.
Using Online Resources for Practice
In today’s digital age, online platforms offer a wealth of tools to enhance your learning experience. These resources provide a variety of exercises, interactive lessons, and video tutorials that cater to different learning styles. They allow students to practice concepts at their own pace, making it easier to revisit difficult topics or explore new ones.
Interactive Practice Tools

Many websites offer interactive quizzes and exercises that allow you to test your understanding in real-time. These platforms often provide instant feedback, helping you identify areas that need improvement. Some even track your progress over time, offering personalized recommendations based on your performance.
Video Tutorials and Step-by-Step Guides
For visual learners, video tutorials can be an invaluable resource. These videos break down complex concepts into manageable steps, providing clear explanations and visual aids to reinforce learning. Many platforms offer step-by-step guides that walk you through problems, making it easier to understand how to approach similar questions on your own.
Reviewing Key Skills for Success
To excel in any subject, it is essential to strengthen the foundational skills that support more complex concepts. A solid grasp of core abilities enables students to approach challenges with confidence and build on their knowledge effectively. Regular practice and review are crucial for reinforcing these skills and ensuring long-term success.
Understanding Basic Operations
One of the first steps toward mastery is being comfortable with basic operations such as addition, subtraction, multiplication, and division. These fundamental skills serve as the building blocks for solving more advanced problems. Practice these operations regularly to ensure speed and accuracy, which are essential for tackling more difficult tasks.
Problem-Solving Strategies
Developing problem-solving skills is key to overcoming obstacles. Learning how to break down complex questions into smaller, more manageable parts helps students stay organized and focused. Whether it’s by identifying patterns or applying logical reasoning, strong problem-solving techniques can lead to more efficient and accurate solutions.