
In this section, we will guide you through the essential solutions to various problems encountered in advanced mathematical topics. These solutions are designed to help you understand complex concepts and improve your problem-solving abilities. By exploring these answers, you can gain a deeper insight into the methods and techniques that are crucial for mastering the subject.
Comprehension and practice are vital to progressing in these areas. With the provided explanations, you can not only verify your results but also refine your understanding of the core principles. Each solution is accompanied by a thorough breakdown of the steps involved, ensuring that you can follow the reasoning behind every calculation and logic used.
As you work through these problems, take time to reflect on the strategies presented, and consider how they relate to the broader concepts in the course. Whether you’re reviewing or tackling new challenges, these solutions will help build a strong foundation for continued success in more advanced topics.
Secondary Math 2 Module 4 Answer Key

This section provides detailed solutions to the problems presented in the fourth unit of the course. By examining these explanations, you will gain clarity on how to approach and solve each question effectively. The goal is to enhance understanding by breaking down complex steps into easy-to-follow instructions, ensuring a comprehensive grasp of the material.
Each solution is structured to highlight the logical progression from start to finish, helping you not only verify your results but also deepen your understanding of the methods used. This will improve your ability to apply these techniques in future challenges, fostering greater confidence in your skills.
Reviewing these solutions offers an opportunity to refine problem-solving strategies and strengthen your overall command of the subject. Through consistent practice, you’ll be better prepared for more advanced topics, reinforcing the foundational knowledge necessary for success in the course.
Overview of Module 4 Answers
This section provides a comprehensive summary of the solutions for the tasks covered in the fourth unit of the course. Each response is carefully crafted to guide you through the necessary steps, highlighting key concepts and strategies essential for solving the problems effectively. By working through these solutions, you can gain a better understanding of the methods involved and apply them to similar challenges.
Understanding the Problem-Solving Process
The explanations are designed to break down the problem-solving process into manageable steps, ensuring clarity and focus. By analyzing each solution, you will be able to recognize patterns, improve your calculation techniques, and develop a deeper insight into the underlying principles.
Improving Your Problem-Solving Skills
With consistent practice and review of these solutions, you can enhance your ability to approach and solve complex tasks. The key to success lies in understanding the reasoning behind each step, which will help you tackle future challenges with confidence. Refining your skills in this way will lay the foundation for mastering more advanced topics.
Key Concepts in Secondary Math 2
This section focuses on the fundamental principles and techniques that are central to the content covered in the second level of the course. By understanding these core concepts, you can build a strong foundation for solving a wide range of problems. The goal is to familiarize you with the critical ideas that will help you not only complete assignments but also approach complex tasks with a clearer mindset.
Mastering these concepts will allow you to apply them in various contexts, reinforcing your ability to think critically and solve problems efficiently. Each concept is interconnected, and understanding how they relate to one another is essential for progressing through more advanced topics. With practice, you’ll be able to confidently navigate through each challenge and expand your mathematical proficiency.
How to Use the Answer Key
This section explains how to effectively utilize the provided solutions to improve your understanding of the material. The purpose of reviewing these responses is not just to check if your results are correct, but also to learn the reasoning and techniques behind each step. By following the detailed breakdowns, you can strengthen your problem-solving approach and apply these methods to future exercises.
Step-by-Step Review of Solutions
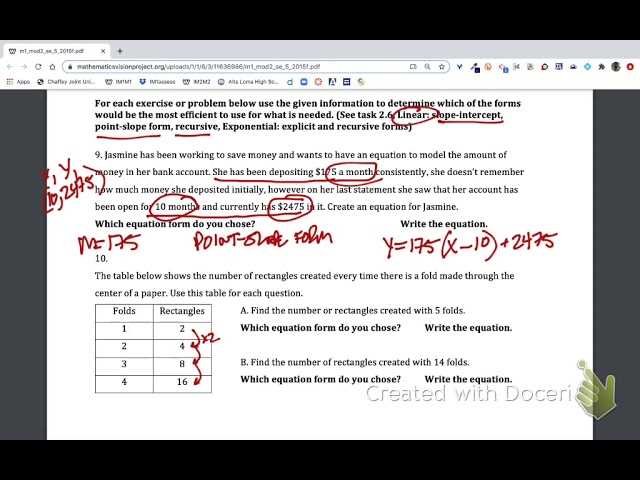
Start by carefully examining each step in the provided solutions. Focus on how each calculation is performed and the logic behind the approach. This process will help you internalize the methods used, making it easier to replicate them in similar problems.
Identify Key Techniques for Improvement
While reviewing the solutions, pay attention to recurring strategies and concepts that you may have missed or misunderstood. Identifying these will help you refine your approach and tackle more challenging problems with confidence. The goal is to use the solutions as a learning tool rather than just a verification method.
Common Mistakes in Module 4
In this section, we will highlight some of the most frequent errors encountered when working through the exercises in this unit. These mistakes are often the result of misunderstandings or misapplications of key concepts, and recognizing them can help you avoid similar pitfalls in the future. By learning from these common errors, you can enhance your problem-solving skills and ensure a more accurate approach to the material.
Misunderstanding Key Concepts
A common issue occurs when core principles are not fully understood or applied incorrectly. This can lead to mistakes in calculations or logical reasoning. It is essential to review foundational concepts carefully and ensure you understand how they connect to the problems at hand.
Overlooking Important Details
Another frequent mistake is skipping over small but important details in the problem or the solution process. Whether it’s a missing negative sign or an overlooked step, these details can significantly affect the outcome. Paying close attention to every part of the problem is crucial for achieving the correct result.
Understanding the Module 4 Problems
In this section, we will focus on gaining a deeper understanding of the problems presented in this unit. Each problem is designed to test your grasp of key concepts and your ability to apply them in various contexts. By carefully analyzing the structure and requirements of each question, you can approach them more effectively and with greater confidence.
Before jumping into the calculations, it is important to break down the problem and identify the critical information. Pay attention to what is being asked and how the data provided relates to the solution. Understanding the context of each problem will allow you to choose the appropriate methods and strategies for solving it.
Step-by-Step Solutions for Each Question
This section provides a detailed breakdown of how to solve each problem in this section of the course. The step-by-step explanations are designed to walk you through the thought process and methodology required to arrive at the correct solution. By following these steps, you will develop a deeper understanding of the techniques involved and how they can be applied to similar challenges.
Solution Breakdown
Each question is tackled by breaking it down into smaller, manageable steps. This ensures that no part of the problem is overlooked and helps clarify the process from start to finish. Carefully following each step will help reinforce your understanding of the concepts being tested.
Applying Problem-Solving Techniques
As you work through the solutions, pay close attention to the techniques being used and how they relate to the problem. This will not only guide you to the correct answer but also enhance your overall problem-solving skills.
| Step | Action | Explanation |
|---|---|---|
| 1 | Identify the key information | Highlight the critical values and what is being asked in the problem. |
| 2 | Choose the appropriate method | Select the correct mathematical technique or formula to use. |
| 3 | Perform the calculations | Carry out the operations step by step, ensuring accuracy at each stage. |
| 4 | Review the solution | Double-check your work to confirm the final result is correct. |
Tips for Mastering Math 2 Topics

To excel in the topics covered in this section of the course, it’s essential to develop a solid understanding of the fundamental concepts and approaches. With the right strategies, you can improve both your problem-solving skills and your ability to apply various techniques effectively. Here are some practical tips to help you master the material and achieve success in your studies.
Effective Study Strategies
- Practice regularly: Consistent practice is key to mastering any topic. Work through problems daily to reinforce your understanding and improve your speed.
- Focus on key concepts: Pay attention to the core principles that underpin each lesson. Understanding these will help you approach complex problems with confidence.
- Review solutions: After completing problems, carefully review the solutions to identify any errors or areas where you can improve.
- Use visual aids: Diagrams, graphs, and charts can help you better understand abstract concepts and visualize relationships between variables.
Approaching Challenges with Confidence
- Break down problems: When faced with a complex problem, break it into smaller, more manageable parts to simplify the process.
- Stay organized: Keep track of the methods and techniques you’ve used. A well-organized approach makes it easier to recall solutions when faced with similar tasks.
- Learn from mistakes: Mistakes are an essential part of the learning process. Analyzing your errors will help you identify weak spots and improve your approach.
How to Check Your Answers Effectively
Checking your work is a crucial part of the learning process. It not only helps you identify mistakes but also reinforces the correct methods and techniques you’ve learned. Effective verification allows you to improve your problem-solving skills and boosts your confidence in applying the concepts correctly. Here are some strategies to help you check your solutions thoroughly and efficiently.
Steps for an Effective Review
- Revisit the question: Before verifying your solution, reread the problem to ensure you fully understand what is being asked.
- Check each step: Review every part of your solution process. Make sure you’ve followed the correct procedure and haven’t skipped any steps.
- Use reverse calculations: For certain problems, you can check your result by working backward. This helps confirm if the initial solution was correct.
- Test with different numbers: Substitute values into the original problem to see if they produce the same result as your solution.
Common Mistakes to Avoid During Verification
- Overlooking details: Small errors, like a misplaced decimal or missing sign, can have a big impact. Double-check every detail to avoid these simple mistakes.
- Rushing the process: Avoid speeding through the review. Take your time to carefully assess each part of your work.
- Not understanding why: Simply confirming that an answer is correct isn’t enough. Make sure you understand why the solution works and why the steps are correct.
Resources to Supplement Your Studies
To deepen your understanding and enhance your learning experience, it’s essential to utilize additional resources outside of your main materials. These resources provide alternative explanations, practice opportunities, and interactive tools that can help clarify difficult concepts and reinforce what you’ve already learned. By incorporating a variety of learning aids, you can strengthen your knowledge and boost your confidence in tackling new challenges.
Helpful Tools and Materials
- Online tutorials and videos: Platforms like YouTube, Khan Academy, and Coursera offer video lessons that explain concepts in different ways, providing visual aids and step-by-step guides.
- Practice worksheets: Many educational websites offer downloadable worksheets with extra problems to practice, which is a great way to reinforce key skills.
- Interactive learning apps: Apps such as Desmos or Wolfram Alpha allow you to experiment with various problems and instantly check your solutions, providing immediate feedback.
- Study groups: Collaborating with peers in study groups can provide fresh perspectives on difficult topics, and explaining concepts to others is an effective way to solidify your own understanding.
Books and Reference Guides
- Textbooks: Textbooks often offer in-depth explanations, examples, and additional practice problems that can provide a more comprehensive understanding of the subject.
- Solution manuals: Solution manuals provide complete step-by-step answers, allowing you to check your work and understand the correct process for solving problems.
- Online forums: Websites like Stack Exchange or Reddit’s math communities are great for asking questions and getting insights from others who have mastered the material.
Importance of Practice for Math Success
Consistent practice is essential to mastering any subject, and this is especially true for topics that require problem-solving skills. The more you practice, the more familiar you become with the concepts and techniques necessary to solve complex problems. By regularly working through exercises, you reinforce your understanding, develop stronger problem-solving strategies, and build the confidence needed to tackle even the most difficult challenges.
How Practice Improves Performance
- Enhances problem-solving skills: Repeated exposure to various problems helps you learn different approaches, making it easier to tackle new and unfamiliar questions.
- Increases speed and accuracy: Regular practice allows you to become quicker at identifying solutions, reducing the chances of making mistakes under time constraints.
- Builds confidence: The more you practice, the more confident you become in your ability to solve problems and apply your knowledge correctly.
Tracking Progress Through Practice
It’s important to monitor your progress as you practice. Tracking your performance over time helps you identify areas where you’ve improved and areas where you might need further attention. Here’s how you can track your progress effectively:
| Practice Session | Problem Difficulty | Time Taken | Accuracy |
|---|---|---|---|
| Session 1 | Medium | 15 minutes | 80% |
| Session 2 | Hard | 20 minutes | 75% |
| Session 3 | Easy | 10 minutes | 95% |
By keeping track of how long it takes to complete problems, how difficult they are, and your accuracy, you can spot trends in your performance and determine where more practice is needed. Over time, this will help you improve and prepare more effectively for assessments.
Applying Math 2 Concepts in Real Life
The ability to apply the concepts learned in the classroom to real-world situations is a crucial skill. Many of the ideas and techniques studied in this subject can be directly used in daily activities, from making financial decisions to analyzing data and solving problems in various fields. By understanding how these abstract concepts translate into practical applications, you gain a deeper appreciation of their value and usefulness beyond the classroom.
Everyday Applications of Key Concepts
- Budgeting and Financial Planning: Skills such as working with percentages, fractions, and equations are essential for managing personal finances, calculating expenses, and setting savings goals.
- Building and Construction: Geometry and measurements are fundamental in tasks like designing buildings, determining areas, and calculating materials needed for projects.
- Shopping and Discounts: Understanding proportions and percentages can help you calculate discounts, sales tax, and the final price of items, allowing you to make smarter purchasing decisions.
- Data Analysis: Statistical methods learned in this field are used to interpret data, whether in business, healthcare, or sports, helping make informed decisions based on trends and patterns.
Real-Life Examples of Problem Solving
- Construction Projects: If you’re building a fence, you’ll use geometry to calculate the length of materials needed based on the measurements of the area to be fenced.
- Cooking and Recipe Adjustments: Ratios and proportions are used when adjusting recipe quantities for more or fewer servings. For example, increasing or decreasing the amount of ingredients based on the number of people you’re cooking for.
- Travel Planning: When planning a trip, distance, speed, and time calculations are crucial. You can use algebraic equations to calculate travel time based on speed and distance or to optimize travel routes for efficiency.
Understanding how to apply these concepts in everyday situations not only makes math more relevant but also enhances your problem-solving skills in all areas of life. By connecting what you learn in the classroom to real-world applications, you will develop practical skills that benefit both your personal and professional life.
Where to Find Additional Help
If you’re struggling to grasp certain concepts or need extra support with your studies, there are several resources available to help you improve your understanding. Whether you prefer personalized tutoring, online platforms, or self-paced study materials, you can find tools that fit your learning style. Seeking additional help is a smart approach to reinforcing your knowledge and ensuring your success in solving complex problems.
Online Platforms and Websites
- Khan Academy: This free educational resource provides comprehensive lessons, practice problems, and tutorials on a wide range of topics, including those relevant to your course.
- Coursera: Online courses offered by universities and institutions, covering various subjects and offering structured lessons that can help you strengthen weak areas.
- EdX: Another platform that offers free and paid courses, with video lectures and quizzes that can help reinforce your knowledge in specific areas.
- Wolfram Alpha: A computational knowledge engine that provides step-by-step solutions to various types of problems, allowing you to understand how to approach different types of questions.
Study Groups and Tutoring
- Peer Study Groups: Forming or joining a study group with classmates can provide a collaborative environment for discussing problems, sharing solutions, and clarifying doubts together.
- Private Tutors: Hiring a tutor or seeking help from your teacher after class can offer you personalized instruction tailored to your individual needs.
- School Resources: Many schools have academic support centers or peer tutoring programs where students can get additional help with difficult topics.
Printed and Digital Books
- Textbooks: Review the course textbook, as it often contains practice problems and detailed explanations that can help you understand the material better.
- Study Guides: Consider purchasing or borrowing a study guide that offers practice questions and detailed solutions to commonly tested problems.
- Digital Resources: E-books, apps, and downloadable worksheets are also available to give you extra practice and explanations outside of class.
With so many resources available to assist you, you can easily find the right help to improve your skills. Whether it’s through online platforms, one-on-one tutoring, or peer collaboration, using these tools will enhance your understanding and boost your confidence in solving complex problems.
Alternative Methods for Solving Problems

There are multiple approaches to solving problems that can provide valuable insights beyond traditional methods. These techniques help to simplify complex tasks, improve accuracy, and increase efficiency. Exploring different problem-solving strategies allows individuals to find the most effective way to tackle challenges, adapting methods based on the specific nature of the problem at hand.
Visualizing the Problem

One powerful method is to visualize the problem. By using diagrams, charts, or graphs, you can better understand relationships and patterns, which may not be immediately clear from the written problem. This method is particularly effective for spatial or geometric problems, as well as for organizing data in a structured manner.
Estimation Techniques
Estimation is an excellent strategy when you need a quick, rough answer or when precision is not critical. Approximating values can help you quickly assess if an answer is reasonable, and it can be particularly helpful for large or complicated problems. It’s an efficient way to narrow down possible solutions without needing to solve every detail.
Breaking Down the Problem
When faced with a complex problem, breaking it into smaller, manageable components can make it easier to solve. By isolating individual parts of the problem, you can address them one at a time, ultimately leading to a complete solution. This method reduces the overwhelming nature of large tasks and promotes a more systematic approach to problem-solving.
Using Known Formulas
Applying known formulas and mathematical rules is a tried-and-true approach that simplifies many problems. Once you recognize the type of problem, you can apply the corresponding formula to reach a solution more quickly and accurately. This approach is especially helpful for repetitive calculations or standardized problems.
Trial and Error
Trial and error involves testing different solutions until you find one that works. While this method can be time-consuming, it is effective when there is no clear method to follow. By experimenting with different approaches, you gain deeper insights into the problem and improve your intuition for future problems.
Collaborative Problem Solving

Working with others can offer new perspectives and creative solutions. Collaborative problem-solving allows you to share ideas and approaches, leading to a more thorough understanding of the problem. Group work can stimulate ideas that might not have been considered when working alone, and peer feedback often provides valuable clarity.
| Method | Advantages | Best Used For |
|---|---|---|
| Visualization | Clarifies complex relationships and structures | Geometric and data-related problems |
| Estimation | Quick, rough solutions for large problems | Checking reasonability, large-scale calculations |
| Breaking Down the Problem | Simplifies complex tasks into smaller steps | Multi-step and complex problems |
| Using Formulas | Efficient for repetitive problems | Standardized and equation-based problems |
| Trial and Error | Works when no clear method is available | Unknown problems or when methods are unclear |
| Collaborative Solving | Promotes creative solutions through teamwork | Group work, brainstorming, peer feedback |
By utilizing these alternative methods, you can approach problems from different perspectives, making the problem-solving process more efficient and comprehensive. Whether it’s visualizing, estimating, or collaborating, these techniques provide flexibility and adaptability when tackling complex challenges.
How Module 4 Builds on Previous Concepts
The structure of the course is designed to reinforce foundational knowledge while introducing more advanced ideas. In this part of the curriculum, students apply the concepts learned earlier and expand on them, developing a deeper understanding. This progression helps to solidify key principles and prepares learners to tackle more complex challenges. The concepts explored in this section are closely linked to earlier lessons, creating a bridge between basic skills and higher-level problem-solving techniques.
Strengthening Core Skills
As learners advance, they revisit previously covered topics, reinforcing their understanding through application and practice. This cyclical approach ensures that students retain essential skills and can adapt them to new situations. For example, basic algebraic principles are revisited and extended to solve more intricate problems, helping to establish a strong foundation for the more advanced methods that will follow.
Introducing Advanced Techniques
Building on the concepts learned in earlier sections, this part of the course introduces more advanced techniques that are essential for solving increasingly complex problems. These new methods often rely on the skills developed in previous lessons, enabling students to solve problems more efficiently and with greater precision. By introducing new strategies in the context of familiar material, learners can more easily grasp these advanced techniques and see how they integrate with their prior knowledge.
Overall, the approach taken in this section emphasizes the interconnectedness of ideas and allows students to gradually build on what they already know, resulting in a more cohesive and comprehensive understanding of the subject.
Reviewing Your Work for Accuracy
Ensuring the correctness of your solutions is an essential part of the learning process. After solving a problem, it’s important to carefully review each step to confirm the accuracy of your calculations and reasoning. This practice not only helps identify potential mistakes but also reinforces your understanding of the concepts involved. By following a systematic approach to review, you can improve both your problem-solving skills and your confidence in handling more complex tasks.
Steps to Review Your Work
To effectively check your work, consider the following steps:
- Revisit the Problem Statement: Ensure you fully understand the question and what is being asked before verifying your solution.
- Double-Check Calculations: Go over your calculations step-by-step to catch any arithmetic or algebraic errors.
- Verify the Solution: Compare your final answer with the expected outcome or known benchmarks, if available, to ensure it makes sense.
- Re-evaluate Your Approach: Assess whether the method you used is the most efficient and appropriate for the problem.
Common Pitfalls to Look For

While reviewing, keep an eye out for common mistakes such as:
- Sign errors: Make sure all signs (positive/negative) are correct, especially when dealing with equations and expressions.
- Misreading the question: Always ensure that you have addressed all parts of the problem accurately.
- Forgetting steps: Sometimes, crucial steps in a process can be skipped or overlooked, leading to incorrect results.
By applying these strategies and being thorough in your review process, you can ensure your work is accurate and avoid unnecessary errors. Regular review helps reinforce learning and ensures mastery of the concepts you’ve studied.
Preparing for the Next Module
After completing a set of lessons or exercises, it’s important to prepare for the upcoming topics to ensure continued success. This phase involves reviewing the material you’ve already covered, identifying any gaps in your understanding, and strengthening your foundational knowledge. Effective preparation not only improves your grasp of future concepts but also boosts your confidence in tackling new challenges.
Review Previous Concepts: Before diving into new material, take time to revisit the key ideas and techniques you’ve already learned. This will reinforce your understanding and make it easier to relate new information to what you’ve previously studied. Focus on areas that felt challenging or unclear during the past lessons, and aim to strengthen your grasp of those concepts.
Preview Upcoming Topics: Familiarize yourself with the main ideas and methods that will be covered in the next set of lessons. This can involve reading ahead in your textbook, watching instructional videos, or reviewing practice problems. Knowing what to expect can give you a clearer roadmap and make the learning process smoother and more intuitive.
Set Goals for Progress: Define specific objectives for your study sessions. These could include mastering certain skills, achieving specific practice goals, or improving speed and accuracy in solving problems. Setting clear and measurable goals will help you stay focused and motivated as you work through the new material.
Practice Continuously: Learning is reinforced through repetition. Regular practice is essential for internalizing concepts and improving problem-solving abilities. Even outside of structured lessons, work on exercises, and engage with the material through different formats, such as quizzes, interactive tools, or study groups.
By preparing systematically for the next set of lessons, you will build a stronger foundation, feel more confident, and improve your overall understanding of the subject. This proactive approach to learning helps you stay ahead and ready to face new challenges with ease.
Improving Problem-Solving Skills in Math
Developing strong problem-solving abilities is crucial for mastering any subject, especially when faced with complex challenges. Strengthening your problem-solving skills requires a combination of critical thinking, practice, and strategy. By improving these skills, you can approach each problem with more confidence and efficiency, leading to better understanding and outcomes.
Understand the Problem First: The key to solving any problem is to fully comprehend what is being asked. Take the time to read the question carefully and identify the given information and what needs to be found. Break the problem into smaller, manageable parts and make sure you understand the underlying concepts before attempting to solve it.
Use a Step-by-Step Approach: One effective strategy is to tackle problems in a systematic way. Start with the simplest part of the problem and work through each step methodically. This helps prevent mistakes and ensures you are logically progressing towards the solution. Writing down each step clearly also makes it easier to track your progress and check for errors.
Learn from Mistakes: Mistakes are an essential part of the learning process. If you encounter an error, don’t be discouraged. Review where you went wrong, understand the mistake, and correct it. This reflection helps solidify your understanding and improves your ability to avoid similar errors in the future.
Practice Regularly: Just like any other skill, problem-solving improves with consistent practice. Work on a variety of problems, gradually increasing the difficulty level. The more problems you solve, the more strategies you develop, and the faster and more efficient you become at solving new challenges.
Seek Different Perspectives: If you’re stuck on a problem, consider different methods or approaches to find the solution. There may be alternative strategies or techniques that make the process easier. Studying different problem-solving methods can expand your toolkit and make you more adaptable to different types of challenges.
By building these skills, you will not only improve your ability to solve problems but also enhance your overall critical thinking and analytical abilities. With consistent effort and the right approach, your problem-solving skills will grow stronger over time.