
When it comes to assessing your skills in solving mathematical problems, there are various types of tasks that require both understanding and strategy. These exercises test not only your knowledge but also your ability to apply logical thinking and problem-solving techniques.
To succeed, it’s crucial to be familiar with a wide range of techniques. From simplifying complex expressions to solving intricate numerical puzzles, each problem offers a unique opportunity to strengthen your grasp on essential concepts. With the right approach, you can confidently navigate through these challenges.
Preparation plays a key role in performing well. Knowing the typical structure and types of tasks you might face allows you to plan ahead and approach each with the necessary tools. Practice is equally important–working through examples builds familiarity and sharpens your problem-solving abilities.
Mathematical Challenges and Solutions
In this section, we explore a range of common tasks designed to assess your problem-solving abilities. Each challenge requires applying a variety of mathematical strategies to arrive at the correct solution. Understanding the different types of problems is crucial to developing a confident approach to tackling them.
Key Problem Types to Prepare For
- Equations involving variables and constants
- Complex number manipulations
- Linear expressions and their simplification
- Polynomial factorization
- Solving for unknowns in real-world scenarios
Effective Strategies for Solving Problems
- Identify the structure of the problem to understand what methods are required.
- Break down the task into smaller, manageable steps.
- Use logical reasoning to eliminate unnecessary information and focus on the key elements.
- Always double-check your work to avoid simple calculation mistakes.
- Review similar examples to reinforce your understanding.
Common Mathematical Problems You May Face
When solving mathematical tasks, several problem types frequently appear. These challenges often require a mix of techniques, from simplifying expressions to solving for unknowns in various scenarios. Mastering these types of problems is key to developing a strong foundation in math.
Below are some of the most common problem types you might encounter:
- Equations with multiple variables
- Word problems that require translating real-life situations into mathematical expressions
- Systems of equations that need to be solved simultaneously
- Quadratic equations and their factorizations
- Rational expressions and simplifying them
Tips for Solving Mathematical Equations
Solving equations efficiently requires a clear understanding of the underlying concepts and the ability to apply various strategies. Each equation may require a different approach, but following a systematic method can greatly improve your accuracy and speed. The key is to break down the problem and tackle it step by step.
Here are some tips to keep in mind when solving equations:
| Tip | Description |
|---|---|
| Isolate the Variable | Focus on moving all terms involving the unknown to one side of the equation. |
| Combine Like Terms | Simplify both sides of the equation by combining similar terms. |
| Check Your Work | Always verify your solution by substituting it back into the original equation. |
| Use Inverse Operations | Apply inverse operations to cancel out terms and solve for the unknown. |
| Practice with Different Types | Familiarize yourself with different equation formats to increase flexibility in problem-solving. |
Understanding Polynomial Equations in Tests
Polynomial equations often appear in assessments, requiring a good grasp of the principles behind them. These equations involve terms with different powers of a variable, making them more complex than simple linear expressions. The challenge lies in recognizing the degree of the equation and applying appropriate methods for simplification and solving.
To effectively tackle these problems, it is essential to follow a structured approach. Identifying the highest power of the variable, factoring terms, and applying the appropriate theorems are all key steps in finding a solution. Working through examples and practicing different types of polynomial expressions will help build confidence and enhance problem-solving skills.
Trigonometric Functions in Assessments
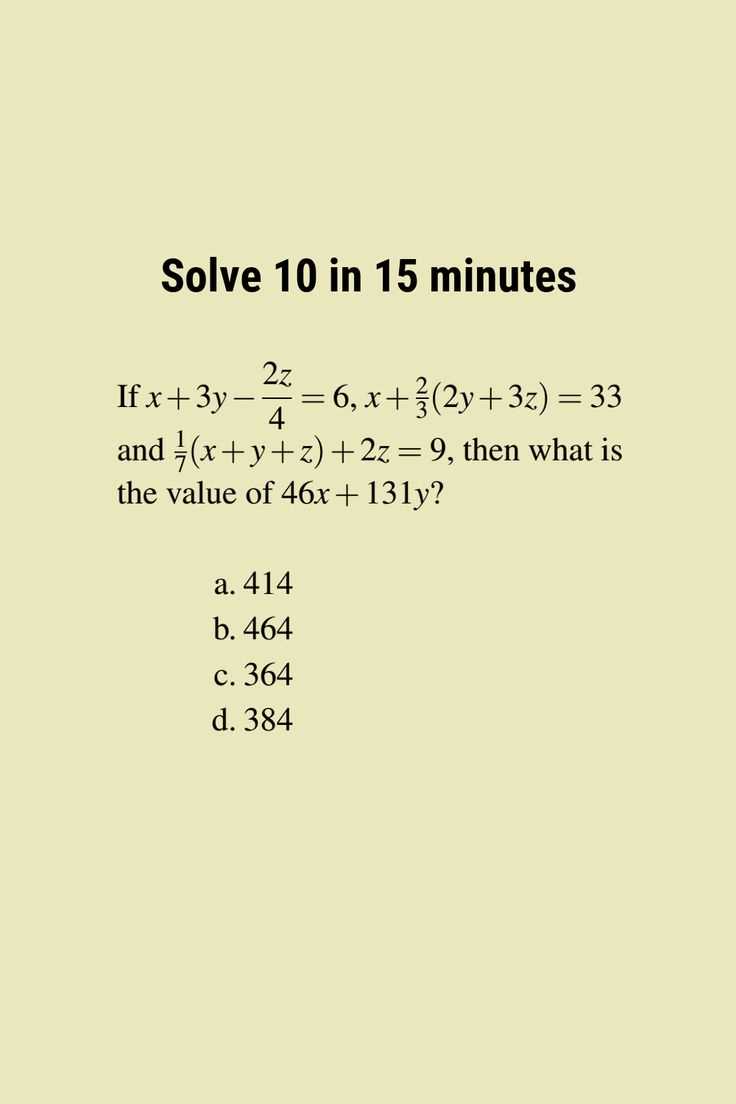
Trigonometric functions are often included in mathematical challenges, testing your ability to work with angles and their relationships to various ratios. These functions, such as sine, cosine, and tangent, play a key role in solving problems that involve periodic patterns, waves, and angles in triangles. Understanding how to apply these functions effectively is essential for success.
When encountering these problems, it’s important to recognize which function is most appropriate for the situation. Whether simplifying expressions or solving for unknown values, familiarity with the basic properties and identities of trigonometric functions will help in navigating these tasks with confidence.
How to Tackle Word Problems Efficiently
Word problems often present a challenge due to their real-world context, requiring you to translate everyday situations into mathematical expressions. The key to solving these problems effectively is breaking them down into manageable steps and carefully identifying the necessary information. By following a clear, structured approach, you can solve these tasks with greater accuracy and speed.
Steps to Approach Word Problems
- Read the problem carefully and underline key information.
- Translate the words into mathematical symbols or equations.
- Organize the data to simplify the task (e.g., use tables or lists).
- Choose the right method or formula based on the type of problem.
- Check your final solution by substituting it back into the context of the problem.
Common Pitfalls to Avoid
- Skipping the step of identifying all relevant details in the problem.
- Overcomplicating the problem by applying unnecessary operations.
- Forgetting to double-check your results to ensure they make sense in the real-world context.
Key Concepts for Mastering Algebraic Fractions
Working with fractions that involve variables can be challenging, but with the right understanding, it becomes easier to simplify and solve these expressions. The key is recognizing how to manipulate the terms in the numerator and denominator, as well as knowing when to factor, cancel, or apply other operations. Mastering these techniques is essential for handling more complex mathematical problems.
Essential Techniques for Simplification
- Factorization: Always check if terms in the numerator or denominator can be factored to simplify the fraction.
- Finding the Least Common Denominator (LCD): This technique is crucial when adding or subtracting fractions with different denominators.
- Canceling Common Terms: When you factor the numerator and denominator, cancel out common factors to simplify the expression.
- Multiplying and Dividing: Remember to multiply numerators and denominators directly when working with these operations, and simplify afterward.
Common Mistakes to Avoid
- Misunderstanding negative signs: Pay close attention to how negative signs affect both the numerator and denominator.
- Forgetting to factor: Always look for ways to factor both the numerator and the denominator to simplify expressions.
- Overlooking the LCD: Not finding the least common denominator can lead to incorrect results in addition or subtraction problems.
Steps to Solve Linear Mathematical Equations
Solving linear equations requires a systematic approach that focuses on isolating the unknown variable. By following a step-by-step process, you can break down complex problems into manageable parts. Whether you’re working with simple or more advanced linear problems, understanding the basic steps will help you reach the correct solution efficiently.
| Step | Action |
|---|---|
| Step 1 | Move all terms involving the variable to one side of the equation. |
| Step 2 | Simplify both sides by combining like terms. |
| Step 3 | Isolate the variable by using inverse operations, such as addition or subtraction. |
| Step 4 | Perform any necessary multiplication or division to solve for the unknown. |
| Step 5 | Verify the solution by substituting the value of the variable back into the original equation. |
Strategies for Factoring Quadratic Equations
Factoring quadratic expressions is a critical skill in solving more complex mathematical problems. This process involves rewriting a polynomial as a product of two binomials, making it easier to find the solutions to the equation. The key to factoring successfully is recognizing patterns and applying the right techniques depending on the structure of the equation.
Common Techniques for Factoring
- Factoring by Grouping: This method works well when the equation contains four terms. By grouping terms and factoring each group separately, you can simplify the expression.
- Using the Difference of Squares: If the equation involves a difference of two perfect squares, you can factor it as the product of conjugates.
- Trial and Error: This technique involves finding two numbers that multiply to give the constant term and add up to the coefficient of the linear term.
Steps to Factor a Quadratic Equation
- Write the equation in standard form, ax² + bx + c = 0.
- Identify the values of a, b, and c.
- Find two numbers that multiply to ac and add to b.
- Split the middle term using the two numbers found, then factor by grouping.
- Check your solution by expanding the factored form to ensure it matches the original equation.
Important Theorems and Properties to Know
Understanding key theorems and properties is essential for solving complex mathematical problems. These fundamental principles provide the foundation for working with equations, functions, and expressions. Mastering them will allow you to approach a wide range of challenges with confidence and precision.
Key Theorems and Concepts
- The Distributive Property: This principle allows you to multiply a term across a sum or difference, simplifying expressions.
- The Zero Product Property: If the product of two terms is zero, then at least one of the terms must be zero.
- The Commutative and Associative Properties: These properties govern the rearrangement of addition and multiplication operations without changing the result.
- Exponent Laws: Knowing how to handle powers and exponents, such as the product rule and quotient rule, is crucial for simplifying expressions.
Useful Strategies for Problem-Solving
- Factorization: Recognizing how to break down complex expressions into simpler factors can help in solving equations more effectively.
- Substitution: This technique involves replacing variables with known values to simplify calculations and solve for unknowns.
- Identities: Familiarity with standard identities, such as the Pythagorean identity, aids in simplifying trigonometric and polynomial expressions.
Mastering Mathematical Expressions and Simplification
Working with complex mathematical expressions often involves simplifying them to their most basic form. By breaking down terms, factoring, and combining like terms, you can make solving problems much easier. Mastering these skills allows for more efficient problem-solving and a deeper understanding of the underlying principles.
Key Techniques for Simplification
- Combining Like Terms: Always group similar terms together to reduce the complexity of an expression.
- Distributive Property: Apply this property to eliminate parentheses and simplify expressions, such as a(b + c) = ab + ac.
- Factoring: Look for common factors in terms to rewrite the expression in a simpler form.
- Reducing Fractions: When working with rational expressions, cancel out common factors in the numerator and denominator to simplify.
Steps to Simplify Expressions
- Identify like terms and combine them where possible.
- Apply the distributive property to eliminate parentheses.
- Factor any remaining terms to identify common factors.
- Reduce fractions by canceling out common factors in the numerator and denominator.
- Check your simplified expression by substituting values back to ensure it matches the original equation.
Challenges in Solving Exponential Equations
Solving equations involving exponents can present unique difficulties due to the rapid growth or decay of variables. These types of problems require a clear understanding of how powers and logarithms interact, as well as strategies to isolate the variable. Overcoming these challenges often involves manipulating equations to a form where the variable can be more easily extracted.
Common Issues in Solving Exponential Equations
- Matching Exponents: One of the most challenging aspects is when the equation contains different bases. Transforming the equation into a common base can often be a key step in simplifying the problem.
- Isolating the Exponential Term: Before applying logarithms or other methods, it’s essential to isolate the exponential term. This may involve moving terms or factoring expressions to make the exponential part stand alone.
- Handling Logarithmic Properties: Understanding the properties of logarithms is critical when solving these types of problems. Using the right log rules, such as the product, quotient, and power rules, can simplify the equation significantly.
Approaches to Solve Exponential Equations
- Taking Logarithms: Applying logarithms to both sides of the equation is a common method, especially when you have a variable in the exponent. Choose a base that aligns with the exponent’s base for simpler calculations.
- Equating Exponents: If both sides of the equation have the same base, equating the exponents directly allows you to solve for the variable.
- Graphical Solutions: In cases where algebraic manipulation is difficult, graphing the equation and identifying the point of intersection can provide a visual solution.
How to Approach Systems of Equations
Solving a set of simultaneous equations can seem daunting at first, but breaking the process into manageable steps makes it much more straightforward. By working through different methods and carefully considering the structure of the system, you can find the values of the unknowns efficiently. Whether using substitution, elimination, or matrix methods, understanding each approach will help you tackle these problems with confidence.
Methods for Solving Systems
| Method | Description |
|---|---|
| Substitution | One equation is solved for one variable, and this expression is substituted into the second equation to reduce the system to one equation with one unknown. |
| Elimination | By adding or subtracting the equations, one variable is eliminated, leaving a simpler system to solve for the remaining variable. |
| Graphical Method | The equations are graphed on the same coordinate plane, and the point of intersection provides the solution to the system. |
| Matrix Method | Using matrices to represent the system, this method applies matrix operations to solve for the unknowns more efficiently, especially for larger systems. |
Steps for Efficiently Solving Systems
- Step 1: Choose the most appropriate method based on the structure of the system. For simple systems, substitution or elimination may be sufficient, while more complex systems may require matrices.
- Step 2: Simplify the equations as much as possible to make solving easier. This may involve clearing fractions or combining like terms.
- Step 3: Solve for one variable first, then substitute or eliminate to solve for the others.
- Step 4: Check your solutions by substituting them back into the original equations to ensure consistency.
Preparing for Word Problem Challenges
Word problems often appear in mathematical assessments, requiring you to translate real-world situations into mathematical expressions and equations. The key to solving these types of problems efficiently lies in understanding the context, identifying the unknowns, and applying the appropriate techniques to find the solution. By practicing with a variety of scenarios, you can develop the skills necessary to approach these problems confidently and systematically.
Breaking Down Word Problems
When faced with a word problem, follow these steps to make the process more manageable:
- Understand the scenario: Read the problem carefully and make sure you grasp the situation being described.
- Identify what you need to find: Focus on what the problem is asking for, such as the value of a variable or the relationship between different quantities.
- Assign variables: Represent unknown values with variables to create a mathematical model of the problem.
- Translate words into expressions: Convert the problem’s conditions into equations using operations such as addition, subtraction, multiplication, or division.
Strategies for Solving Word Problems
- Draw diagrams: Visual aids can help clarify relationships between variables and provide a clearer understanding of the problem.
- Set up an equation: Once the relationships are clear, form an equation that represents the situation.
- Solve step-by-step: Break down the problem into smaller, more manageable steps to avoid confusion and make sure each part is solved correctly.
- Check your work: After finding a solution, substitute your result back into the original problem to ensure it makes sense in the context provided.
Reviewing Functions and Their Graphs
Functions play a central role in mathematical analysis, as they describe the relationship between variables. Understanding how to interpret and analyze their graphs is essential for solving problems effectively. The graph of a function provides a visual representation of how one variable depends on another, making it easier to recognize patterns, trends, and key features. By reviewing these concepts, you can sharpen your skills in graph interpretation and enhance your ability to work with different types of functions.
Key Features of Function Graphs
When reviewing graphs of functions, focus on these critical features that help you understand the behavior of the function:
- Intercepts: The points where the graph intersects the x-axis and y-axis. The x-intercept is where the function equals zero, and the y-intercept is the value of the function when x equals zero.
- Asymptotes: These are lines the graph approaches but never actually reaches. Vertical and horizontal asymptotes can reveal important information about the function’s behavior as it approaches infinity.
- Domain and Range: The domain represents the set of input values (x-values) for which the function is defined, while the range represents the possible output values (y-values) that the function can take.
- End Behavior: This refers to how the graph behaves as the input values (x) approach positive or negative infinity. Understanding this helps in predicting the function’s long-term trend.
Tips for Analyzing Function Graphs
To analyze function graphs effectively, consider the following strategies:
- Look for symmetries: Many functions, such as even and odd functions, exhibit symmetrical behavior. Identifying this can simplify your analysis.
- Identify critical points: These include local maxima, minima, and inflection points where the function changes direction. Recognizing these points is crucial for understanding the function’s overall shape.
- Sketch the graph: For some problems, sketching the graph based on the key features you’ve identified can provide insights into the function’s behavior.
- Use transformations: Functions can be transformed through shifts, stretches, and reflections. Understanding these transformations helps you adjust the graph based on changes to the equation.
Handling Inequalities in Algebra Exams
Working with inequalities is an essential skill in solving mathematical problems that involve comparisons between expressions. These problems require a clear understanding of how to manipulate and solve expressions where one side is not necessarily equal to the other, but rather greater than, less than, or something in between. Mastering this concept allows you to determine solution sets and represent them graphically, which is crucial for a wide range of mathematical scenarios.
Key Strategies for Solving Inequalities
When tackling inequality problems, keep the following strategies in mind:
- Isolate the variable: Just like solving equations, begin by isolating the variable on one side of the inequality. This step simplifies the problem and allows you to focus on finding the solution.
- Perform operations carefully: While performing operations on both sides of the inequality, remember that multiplying or dividing by a negative number reverses the direction of the inequality symbol. This is a common mistake that can lead to incorrect results.
- Combine like terms: If there are like terms on either side of the inequality, combine them to make the inequality simpler and easier to solve.
- Consider boundary points: In many cases, inequality problems involve boundary values, such as endpoints in an interval. Consider these points and determine whether they satisfy the inequality.
Graphing Inequalities
Graphing the solution to an inequality can often help visualize the solution set and make the problem more manageable. Here are some tips for graphing inequalities:
- Use a number line: For simple inequalities involving one variable, draw a number line and mark the solution set. Use open circles for strict inequalities (e.g., x ) and closed circles for inclusive inequalities (e.g., x ≤ 5).
- Shade the correct region: After marking the boundary point(s), shade the region that satisfies the inequality. For example, for x > 3, shade to the right of 3.
- Graphing two-variable inequalities: If the inequality involves two variables, graph the corresponding boundary line and use shading to indicate the region that satisfies the inequality. Be sure to use dashed lines for strict inequalities and solid lines for inclusive ones.
Effective Time Management for Algebra Tests
Managing your time efficiently during assessments that require problem-solving is key to performing well. Often, these evaluations consist of a variety of tasks that demand both focus and quick thinking. By organizing your approach, prioritizing tasks, and allocating your time wisely, you can ensure that you complete all sections within the given time frame and avoid unnecessary stress.
Key Strategies for Managing Time Effectively
- Read through all instructions: Before diving into the problems, take a moment to read through all instructions and understand the requirements. This will save you time later and help you avoid mistakes.
- Plan your approach: Assess the difficulty level of each task and allocate your time accordingly. Tackle the easier problems first to build confidence and save more time for complex ones.
- Set time limits: For each section or problem, set a personal time limit. Stick to this limit, and if you get stuck, move on to the next task. You can always come back later if time permits.
- Break tasks into smaller steps: Large problems can seem overwhelming, but breaking them down into smaller, manageable steps can help you stay focused and make quicker progress.
- Keep track of time: Regularly check the clock to monitor your progress. Being aware of time allows you to adjust your pace and avoid rushing at the end.
Tips for Efficiency During the Test
- Eliminate unnecessary steps: Simplify your approach by identifying shortcuts or methods that allow you to reach the solution faster. This is especially useful in problems involving repetitive steps.
- Stay calm and focused: Stress can waste time. Stay calm, breathe, and concentrate on the problem at hand. A clear mind leads to better performance.
- Review your work: If time allows, reserve the last few minutes for reviewing your solutions. Double-checking your work can help catch simple errors.