
Mathematics can be challenging, especially when it comes to mastering specific concepts. Whether it’s understanding complex shapes, angles, or measurements, students often seek additional help to grasp these ideas. There are platforms available that provide step-by-step solutions, making learning more accessible and manageable.
Effective tools allow learners to approach difficult problems with clarity, offering structured explanations that break down complex theories into understandable steps. With the right guidance, students can improve their problem-solving abilities and gain confidence in their skills.
Whether for homework help or mastering difficult topics, these platforms offer a comprehensive approach that caters to all learning needs. By presenting solutions in a clear and organized manner, learners can follow along and tackle challenges more efficiently.
Platoweb Geometry Help and Solutions
Mastering mathematical concepts can be overwhelming, particularly when dealing with complex shapes, measurements, and spatial reasoning. To help students navigate these challenges, there are comprehensive platforms designed to break down difficult problems into simple, manageable steps. These tools offer detailed explanations that guide learners through each stage, ensuring they develop a clear understanding of the subject matter.
Step-by-Step Explanations for Every Problem
One of the primary advantages of such platforms is their ability to offer structured, step-by-step solutions. These guides take students through each part of a problem, explaining the necessary formulas, rules, and concepts. By following these instructions, learners can replicate the process on similar questions and improve their overall understanding.
Improving Problem-Solving Skills
By regularly engaging with these platforms, students can enhance their problem-solving abilities. As they solve more problems, they gain confidence and refine their approach to tackling new challenges. The interactive nature of these resources encourages learners to think critically and apply what they’ve learned to various situations, strengthening their grasp on key concepts.
Understanding Platoweb for Geometry
Learning to solve mathematical problems related to shapes, sizes, and spatial relationships requires the right approach and resources. An effective platform can help students break down complex challenges into understandable segments, offering structured support that encourages mastery of essential concepts. With these tools, users can engage with the material at their own pace, ensuring they grasp each part before moving on to more difficult topics.
Key Features for Success
These platforms are designed with multiple features that support student learning, providing a thorough understanding of mathematical problems. Some key features include:
- Interactive step-by-step guides that break down problems into smaller tasks
- Clear explanations of important formulas and techniques
- Practice exercises to reinforce learning and test understanding
- Instant feedback to correct mistakes and improve comprehension
How to Navigate the Platform
To get the most out of these resources, students should focus on the following steps:
- Start by reviewing the basics and gradually move to more advanced topics.
- Use the available practice problems to test understanding and reinforce learning.
- Pay attention to feedback provided after each task to identify areas for improvement.
- Repeat exercises to solidify knowledge and build confidence in solving similar challenges.
How Platoweb Answers Simplify Geometry
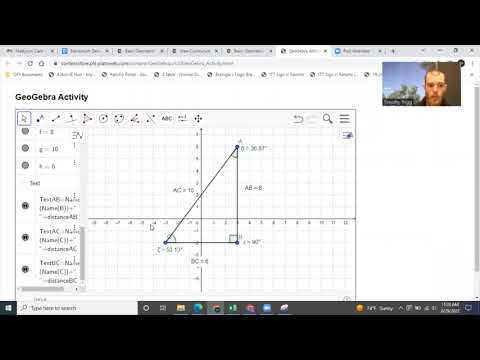
Mathematical concepts involving shapes and spatial relationships can often feel overwhelming. However, with the right resources, complex problems can be broken down into simpler, more manageable steps. These platforms provide a clear and structured approach to solving problems, allowing students to understand the underlying principles and apply them with ease.
Breaking Down Complex Problems
One of the key ways that these platforms simplify learning is by presenting problems in a way that is easy to follow. Instead of overwhelming students with large, complex tasks, the steps are broken into smaller, more digestible parts. This approach helps learners focus on one concept at a time and gradually build up their understanding. The key features include:
- Clear step-by-step breakdown of problem-solving procedures
- Detailed explanations of essential concepts
- Visual aids and diagrams that clarify abstract ideas
- Interactive elements to engage users in the learning process
Reinforcing Knowledge Through Practice
In addition to detailed solutions, these platforms offer practice problems that help reinforce what has been learned. By working through a variety of problems, students gain hands-on experience and confidence in applying their knowledge to different situations. Key benefits of practice include:
- Improved retention through repetition
- Ability to identify patterns and shortcuts in problem-solving
- Real-time feedback to correct mistakes and prevent misunderstandings
- Increased confidence in tackling future problems independently
Top Geometry Problems Solved on Platoweb
Many students struggle with mathematical challenges related to shapes, sizes, and spatial relationships. These problems often require a clear understanding of specific formulas, properties, and strategies for finding solutions. Some of the most common issues students face are made easier through structured guidance and problem-solving techniques provided by effective educational platforms.
Common Problems and Solutions
There are several common types of problems that students frequently encounter when studying spatial relationships. These challenges can be effectively solved with the help of step-by-step guides and visual aids. Some of the top problems include:
- Calculating areas and perimeters of various shapes
- Understanding and solving problems related to angles and their relationships
- Working with the properties of triangles and other polygons
- Solving problems involving the volume of 3D objects
- Applying the Pythagorean theorem in right-angled triangles
How Problems Are Solved
Each of these challenges is approached in a structured way that helps students not only solve individual problems but also grasp the underlying principles that will aid them in future tasks. Key features of this approach include:
- Breaking down the problem into manageable steps
- Applying relevant formulas and theorems
- Using visual representations and diagrams to aid understanding
- Providing practice exercises to reinforce learning and test knowledge
Improving Geometry Skills with Platoweb
Mastering mathematical concepts that involve shapes, sizes, and spatial relationships requires consistent practice and the right guidance. Developing strong skills in this area goes beyond memorizing formulas; it involves understanding how to apply these principles to solve real-world problems. Educational platforms provide valuable resources to help students improve their problem-solving abilities and gain a deeper understanding of these topics.
One effective way to enhance these skills is through interactive learning tools that break down complex problems into simpler steps. These resources not only teach formulas but also show how to use them effectively. Consistent practice and step-by-step guidance help build confidence and proficiency in tackling challenges.
Key Areas to Focus On
Improving skills involves a targeted approach, focusing on the following key areas:
| Topic | Skill to Develop | Recommended Practice |
|---|---|---|
| Shapes and Areas | Identifying properties of various shapes and calculating areas | Practice by solving problems related to rectangles, circles, and triangles |
| Angles | Understanding types of angles and their relationships | Work on angle sums in polygons and complementary angles |
| Volume and Surface Area | Calculating the volume and surface area of 3D objects | Use models and visual aids to apply volume formulas |
| Pythagorean Theorem | Using the theorem to solve for missing sides in right triangles | Practice with various real-life applications |
Focusing on these areas allows students to improve their overall mathematical ability, gaining the skills necessary to solve even the most challenging problems. By engaging with interactive lessons and regular practice, students build both their theoretical knowledge and practical problem-solving abilities.
How to Use Platoweb for Geometry Homework
Completing assignments that involve shapes, measurements, and spatial reasoning can often feel like a daunting task. However, with the right tools and resources, students can efficiently tackle these problems and strengthen their understanding. There are platforms designed to guide learners through each step of their homework, offering structured support and explanations that make difficult concepts more manageable.
Getting Started with the Platform

To make the most of the platform, students should begin by reviewing the problem provided in their homework. The platform allows users to break down the problem into smaller, easier-to-understand segments. By following the organized steps, learners can identify what the problem is asking, which formulas are required, and how to approach the solution.
Step-by-Step Support for Solving Problems
Once students have reviewed the problem, they can proceed to solve it using the provided step-by-step guides. These solutions explain how to apply the necessary formulas and principles to each part of the problem. The platform ensures that learners understand the logic behind each step, reinforcing key concepts and improving their problem-solving skills.
Exploring Platoweb’s Geometry Features
Effective learning tools often come with a range of features designed to help students master complex mathematical concepts. These resources offer interactive elements, detailed explanations, and visual aids that guide learners through difficult tasks. By providing structured support and step-by-step instructions, they help users gain a deeper understanding of the subject matter and improve their overall problem-solving abilities.
Among the most helpful features of such platforms are the visual diagrams, which make abstract ideas more tangible. These features break down complicated problems and offer interactive tools to assist students in visualizing solutions. Additionally, users can access practice problems and receive instant feedback, ensuring they fully grasp each concept before moving on to more advanced topics.
Geometry Answer Key on Platoweb
Having access to a reliable solution guide can greatly enhance a student’s ability to grasp complex concepts in mathematics. An answer key serves as a valuable resource that not only provides correct solutions but also explains the reasoning behind each step. This structured approach helps students identify where they may have gone wrong and understand the logic behind solving problems related to shapes, measurements, and spatial reasoning.
Benefits of an Answer Key
Using a solution guide effectively can provide numerous advantages for students. Key benefits include:
- Clarifying how to approach specific problem types
- Helping students learn the correct application of formulas
- Providing a reference point for understanding the steps taken to reach the solution
- Allowing students to double-check their work and self-correct
Example Problem and Solution Breakdown
To illustrate how a solution guide can help, consider the following example:
| Problem | Solution | Explanation |
|---|---|---|
| Find the area of a triangle with a base of 8 cm and a height of 5 cm. | Area = 1/2 × base × height = 1/2 × 8 × 5 = 20 cm² | To find the area of a triangle, multiply the base by the height and divide by 2. |
| Calculate the volume of a rectangular prism with length 4 cm, width 3 cm, and height 6 cm. | Volume = length × width × height = 4 × 3 × 6 = 72 cm³ | The volume of a rectangular prism is found by multiplying the length, width, and height. |
By following the step-by-step breakdown in the solution key, students can reinforce their understanding of the process and improve their ability to tackle similar problems in the future.
Platoweb Geometry Practice Tests Explained
Practice tests are an essential tool for mastering mathematical concepts. They allow students to apply what they have learned in a simulated environment, helping to identify areas of strength and weakness. These tests typically cover a range of topics, ensuring that learners can test their knowledge across various concepts and problem types, reinforcing their understanding and improving problem-solving skills.
Engaging with these assessments offers valuable insights into how well a student grasps key ideas and which areas may need more attention. By completing a series of practice questions, learners can simulate real exam conditions, gain confidence, and track their progress over time.
How Practice Tests Help Students
Practice tests are beneficial in multiple ways. Here are some of the key advantages:
- Reinforce Learning: Repeated exposure to different problem types helps solidify knowledge and improve recall during actual tests.
- Identify Weaknesses: These tests highlight areas where a student may need further study, allowing for targeted improvement.
- Build Confidence: Regular practice boosts self-assurance, making students feel more prepared when facing challenging problems.
- Track Progress: Taking practice tests periodically provides measurable results, helping students see their improvement over time.
Types of Questions in Practice Tests
Practice tests typically include a variety of question types to assess a wide range of skills. Common question formats include:
- Multiple Choice: These questions test a student’s ability to recognize the correct solution among several options.
- Fill in the Blank: These questions require students to recall and provide the correct answer without any cues.
- Word Problems: These assess a student’s ability to apply mathematical principles to real-world situations.
- Diagrams and Visuals: Some questions incorporate diagrams that students must analyze to answer correctly, helping to visualize concepts.
By regularly taking practice tests, students can not only refine their problem-solving techniques but also gain a deeper understanding of how different mathematical concepts are applied in various scenarios.
Common Geometry Topics on Platoweb

Mathematics encompasses a wide array of topics, each building upon foundational principles. In particular, topics related to shapes, sizes, and spatial relationships are essential for understanding how the world around us works. These subjects are frequently explored in assignments and practice exercises, allowing students to deepen their knowledge and refine their skills in problem-solving. Below are some of the most common areas students encounter when studying these topics.
Key Topics Covered in Lessons
Students working through these lessons often explore a range of core subjects, including but not limited to the following:
- Properties of Shapes: Understanding the characteristics of basic and complex shapes such as circles, triangles, squares, and polygons.
- Measurement of Angles: Learning how to calculate and classify angles, from acute to obtuse and beyond.
- Perimeter and Area: Calculating the perimeter and area of various shapes, including rectangles, circles, and irregular polygons.
- Volume and Surface Area: Determining the volume and surface area of 3D objects like spheres, cylinders, and pyramids.
- Coordinate Geometry: Applying algebraic principles to solve geometric problems on the coordinate plane.
Advanced Topics in Spatial Reasoning
In addition to basic principles, more advanced topics also appear in the curriculum. These may include:
- Transformations: Learning about translations, rotations, reflections, and dilations of shapes on the plane.
- Congruence and Similarity: Understanding the conditions under which shapes are congruent or similar, and how to prove these relationships.
- Trigonometry Basics: Introduction to trigonometric ratios and their applications in solving problems involving right triangles.
- Proofs and Theorems: Developing logical arguments and understanding key theorems, such as Pythagoras’ theorem, to solve problems.
These topics form the foundation of many mathematical studies and provide the tools necessary for tackling increasingly complex problems. By mastering these areas, students gain the ability to apply their knowledge to real-world scenarios and advanced mathematical challenges.
Tips for Navigating Platoweb Geometry
When working through mathematical problems online, it is essential to use the tools and resources effectively. Whether you’re tackling a set of exercises or trying to understand complex concepts, navigating the platform efficiently can significantly improve your learning experience. The following tips will help you make the most of your study time, enhance your understanding, and ensure that you stay on track throughout your assignments.
Use the Available Resources
Most educational platforms provide a variety of helpful resources to assist with learning. Take full advantage of:
- Guides and Tutorials: Many platforms offer step-by-step explanations, guides, and video tutorials. These resources can help clarify difficult concepts and provide additional practice.
- Interactive Tools: Use any interactive diagrams or calculators available to visualize problems, especially those involving shapes and measurements.
- Hints and Explanations: Don’t hesitate to access hints or detailed explanations if you’re stuck on a particular problem. These can provide valuable insights into the solution process.
Organize Your Study Sessions
Staying organized is key to completing assignments efficiently and effectively. Consider these tips to improve your study routine:
- Break Down Tasks: Focus on one section or problem at a time. Dividing your work into manageable parts will prevent you from feeling overwhelmed.
- Set Time Limits: Allocate specific time slots for each problem or lesson. This helps maintain focus and ensures that you’re making steady progress.
- Review Concepts Regularly: Before moving to more complex topics, take time to review previously covered material. This helps reinforce your knowledge and build a solid foundation for new concepts.
Stay Consistent and Practice Regularly
Consistency is crucial when learning mathematical concepts. Set aside regular time for practice, and make sure to go over challenging topics multiple times. Regular practice allows you to:
- Improve Problem-Solving Skills: The more you practice, the more comfortable you’ll become with different types of questions and scenarios.
- Identify Patterns: By working through similar problems, you’ll begin to recognize patterns and strategies for solving them more quickly.
- Boost Confidence: The more you practice, the more confident you’ll feel when tackling new and more difficult problems.
By following these tips, you’ll be better equipped to navigate through mathematical problems and make the most of your learning experience. Remember, persistence and smart study strategies are key to mastering any topic.
Why Platoweb Geometry Answers Are Accurate
The reliability of mathematical solutions relies on precise algorithms and the application of established principles. When it comes to solving problems in this field, the accuracy of results depends on how well the system adheres to these mathematical rules. Platforms that offer assistance with these types of problems ensure that their methods are based on verified mathematical logic and reasoning, which contributes to their credibility and trustworthiness.
Use of Proven Mathematical Methods
One of the key reasons for the accuracy of the solutions provided is the reliance on well-established mathematical techniques. These platforms use algorithms that:
- Follow Standardized Rules: Solutions are derived from universally accepted principles, such as theorems, formulas, and postulates, ensuring consistency and correctness.
- Employ Step-by-Step Processes: The answers are not just the final results but also break down the steps in a logical sequence, which allows for transparency in the reasoning process.
- Address Multiple Problem Types: From basic shapes to complex 3D objects, the platform handles various types of problems with precision by applying specialized formulas and methods.
Advanced Technology and Error-Checking
In addition to sound mathematical practices, the integration of advanced technology further enhances the accuracy of the provided results:
- Automated Calculations: Many platforms incorporate sophisticated computational tools that perform calculations with high accuracy, minimizing human error.
- Real-Time Error Detection: Systems are often designed to identify inconsistencies or errors in calculations and automatically correct them, ensuring that solutions remain reliable.
- Continuous Updates: The platform regularly updates its database of formulas and methods to keep up with any changes or improvements in the field of mathematics.
Through a combination of rigorous mathematical frameworks and cutting-edge technology, these systems ensure that the solutions provided are both accurate and reliable. This precision not only helps students learn more effectively but also boosts their confidence in solving complex problems independently.
Accessing Detailed Geometry Solutions on Platoweb
In order to fully grasp the concepts behind various mathematical problems, having access to comprehensive and well-structured solutions is crucial. This not only aids in understanding the process but also helps learners verify their approach and correct any mistakes. Many educational platforms provide these in-depth solutions, allowing users to dive deeper into the reasoning behind each step and gain a more thorough understanding of the material.
Step-by-Step Breakdown of Problems
One of the key benefits of these resources is the detailed step-by-step explanations. Each solution is broken down into clear, manageable steps, allowing learners to follow along and understand how the result is achieved. These solutions often include:
- Clear Problem Restatement: The original question is often rephrased to ensure clarity and understanding of what is being asked.
- Intermediate Steps: Solutions include every intermediate calculation, showing how each step leads to the next, which reinforces the learning process.
- Visual Aids: Many solutions come with diagrams or illustrations to help visualize the problem and better understand geometric relationships.
Additional Features for Enhanced Learning
Beyond just providing solutions, some platforms include additional features that further enhance learning:
- Explanatory Notes: Many answers are accompanied by brief explanations to clarify complex steps or offer insight into alternative methods for solving the problem.
- Interactive Tools: Some systems allow students to manipulate variables and see how the changes affect the outcome, promoting active learning and deeper engagement.
- Practice Questions: After accessing the solution, learners are often provided with similar practice problems to reinforce the concepts they have just learned.
Accessing these detailed solutions not only helps students achieve better understanding but also empowers them to solve problems more confidently and independently in the future.
How Platoweb Supports Geometry Learning
Learning the intricacies of shapes, angles, and spatial relationships can be challenging, but having the right tools can significantly enhance the educational experience. By offering structured lessons, interactive exercises, and tailored feedback, online platforms provide students with an environment where they can explore and master these concepts at their own pace.
One of the key features is the ability to access a wide range of practice problems that cater to different skill levels. These problems, accompanied by step-by-step solutions, help solidify understanding and encourage critical thinking. Moreover, learners can revisit challenging problems as many times as needed, reinforcing their grasp of the material.
Interactive Learning and Visual Aids
Interactive tools and visual aids play a crucial role in comprehending abstract concepts. By using diagrams, animations, and virtual manipulatives, students can visually explore relationships between different geometric elements. These features allow for a hands-on approach, making abstract ideas more tangible and easier to understand. Common interactive features include:
- Dynamic Diagrams: Interactive visuals that change as the student manipulates parameters, helping them see how different factors influence the overall result.
- Real-Time Feedback: Immediate corrections and explanations that help students understand their mistakes and learn from them.
Personalized Support for Better Learning Outcomes
In addition to providing practice and feedback, many platforms offer personalized learning paths. Based on progress, students receive recommendations for areas to focus on, helping them improve where they are struggling most. This tailored approach ensures that learners remain engaged and consistently make progress.
With these tools and resources, students are not just completing exercises; they are building a deeper understanding of the subject, which empowers them to tackle increasingly complex problems with confidence.
Using Platoweb to Master Geometry Concepts
Mastering the principles of spatial relationships, shapes, and their properties requires a combination of understanding theoretical concepts and applying practical skills. Online learning platforms provide students with the resources and tools they need to develop a deeper understanding of these topics. Through structured lessons, interactive exercises, and guided problem-solving, students can progressively strengthen their skills and confidence in the subject.
One effective way to master these topics is by actively engaging with exercises that challenge and reinforce understanding. These exercises, accompanied by clear explanations and visual aids, allow learners to approach problems from different angles. Repetition and practice are key to retaining knowledge and building proficiency in this field.
Effective Practice Strategies
To become proficient in any subject, consistency and methodical practice are essential. By breaking down complex concepts into smaller, manageable segments, learners can focus on mastering each topic before progressing to the next. The following table outlines a systematic approach to studying the subject:
| Stage | Focus Area | Suggested Activity |
|---|---|---|
| 1 | Understanding Basic Shapes | Review properties and definitions of key shapes, such as triangles, circles, and polygons. |
| 2 | Angle Relationships | Practice identifying complementary, supplementary, and vertical angles in various scenarios. |
| 3 | Transformations and Symmetry | Explore translations, rotations, reflections, and dilations using interactive tools. |
| 4 | Real-World Applications | Apply concepts to solve practical problems, such as calculating area, perimeter, and volume. |
Tracking Progress and Adjusting Focus
Regular self-assessment is an important part of mastering any subject. By regularly tracking progress and revisiting difficult concepts, students can identify areas where additional practice is needed. Most platforms offer progress tracking tools, allowing students to see which areas require more attention. This feedback loop helps guide learning efforts, ensuring that students are always improving.
Incorporating these strategies into daily study routines allows learners to build a strong foundation and develop the confidence needed to solve even the most challenging problems in the field.
Getting the Best Results with Platoweb Geometry
Achieving success in the study of shapes, measurements, and spatial reasoning requires a combination of dedication, effective study techniques, and the right tools. With the right resources, learners can enhance their understanding, gain confidence, and tackle increasingly complex challenges. Utilizing an online platform that provides targeted support and guidance allows students to access a structured learning environment that aligns with their needs and learning pace.
To get the best results in this subject, it’s crucial to approach the material with a clear strategy. Engaging with interactive lessons, solving a variety of problems, and continuously reviewing concepts are all key elements of effective learning. The process of understanding spatial concepts and mastering problem-solving techniques requires consistency and a proactive attitude toward practice.
Maximizing Learning Potential
When using an online learning platform for mastering the subject, there are several strategies that can maximize results:
- Active Participation: Engage with interactive lessons and actively solve problems rather than passively reading through content.
- Frequent Practice: Regular practice of key concepts helps reinforce understanding and build muscle memory for problem-solving.
- Seeking Clarification: Don’t hesitate to revisit difficult topics and ask for explanations or review examples to clarify misunderstandings.
- Reviewing Mistakes: Mistakes are opportunities for growth. Review errors carefully to understand where things went wrong and how to avoid them in the future.
- Setting Goals: Set achievable goals for each study session. Focus on mastering one concept before moving to the next.
Tracking Progress and Adjusting Techniques
Regularly assessing your understanding is a critical aspect of improvement. Many platforms offer tools to track progress and provide instant feedback on completed exercises. Use this feedback to identify areas where further practice is needed. Additionally, revisiting previously studied material periodically will strengthen retention and ensure a solid grasp of all topics.
By following these methods, students can make steady progress and achieve strong results in mastering the field, gaining the knowledge and skills needed for academic success and beyond.
Understanding Geometry in Platoweb’s Platform
Learning about shapes, their properties, and how they relate to one another is a vital aspect of mathematics that plays a critical role in problem-solving and analytical thinking. Online educational platforms offer a dynamic environment where students can engage with these concepts through interactive lessons and structured exercises. These resources are designed to help learners develop a deep understanding of spatial relationships, measurements, and theorems by breaking down complex topics into digestible parts.
One of the key advantages of these learning platforms is the ability to learn at your own pace. Whether you’re reviewing foundational concepts or diving into more advanced topics, the system adjusts to meet the learner’s current understanding, providing personalized guidance where necessary. The platform integrates lessons, practice questions, and instant feedback to facilitate mastery of essential concepts in mathematics.
Core Concepts Covered in the Platform
The platform covers a wide range of topics, ensuring that students build a solid foundation in the subject. Some of the core areas include:
- Shapes and Their Properties: Understanding different types of polygons, circles, and 3D objects, as well as their attributes such as angles, sides, and symmetry.
- Measurements: Learning how to calculate area, perimeter, volume, and surface area of various shapes, which are fundamental skills in the study of spatial properties.
- Transformations: Exploring how shapes move in space, including rotations, translations, and reflections, and how to use these transformations in problem-solving.
- Proofs and Theorems: Gaining proficiency in proving relationships between geometric figures using logical reasoning, with an emphasis on key theorems and postulates.
Interactive Tools for Mastery
The platform is equipped with interactive tools that allow students to visualize geometric problems and solutions. These tools often include drawing features, 3D models, and real-time feedback to help students better understand spatial relationships. By engaging with these features, learners can improve their spatial awareness and problem-solving abilities.
Overall, the platform’s approach to teaching helps demystify complex topics, making them more approachable and easier to understand. With consistent practice and engagement, students can build confidence in their skills and develop a deep, lasting understanding of key mathematical concepts.