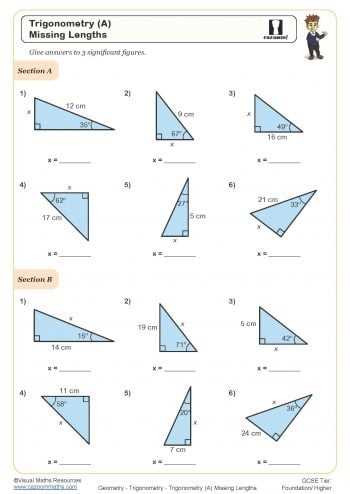
Mathematical challenges often require breaking down complex problems into manageable steps. In this section, we focus on solving specific exercises that test key concepts in angular relationships and geometric analysis. Understanding how to approach these problems is essential for building a strong foundation in mathematical reasoning.
Step-by-step solutions provide clarity on how to tackle different types of exercises. By analyzing various methods, students can gain confidence in applying the right techniques to reach the correct results. Learning to visualize the problems also enhances comprehension and supports accurate problem-solving.
Mastering these types of exercises is a critical skill for students, and reviewing different solution methods helps to refine their mathematical thinking. With enough practice, it becomes easier to identify patterns, apply rules, and work through similar challenges effectively.
8 4 Problem Solutions Overview
Solving mathematical exercises involving angular relationships and geometric properties requires a systematic approach. This section provides insight into the methodology used to solve a variety of problems, breaking down each step for clearer understanding. By analyzing different strategies, students can develop the skills needed to tackle similar challenges with confidence.
Understanding the Approach
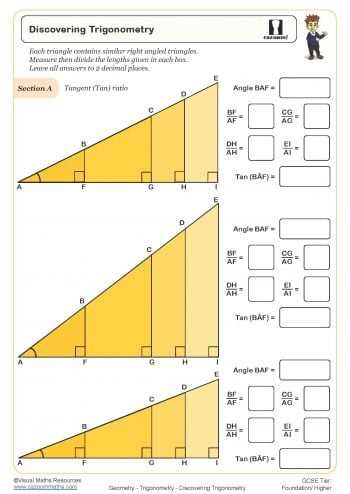
The goal is to analyze each problem and apply appropriate techniques to achieve the desired solution. By using a combination of rules and visual representation, it becomes easier to understand the underlying principles. Each problem presents a unique opportunity to reinforce core concepts while building problem-solving skills.
Step-by-Step Breakdown
The following table outlines the key stages for solving each problem in this set. By reviewing these steps, students can gain a clearer picture of how to approach and work through complex tasks efficiently.
| Step | Description | Example |
|---|---|---|
| 1 | Identify the given values and variables | Recognizing known and unknown values |
| 2 | Apply fundamental relationships between elements | Use of sine, cosine, or other formulas |
| 3 | Simplify the expression to solve for the unknowns | Rearranging equations to isolate variables |
| 4 | Verify the solution for consistency | Double-check the calculations for accuracy |
Understanding Trigonometric Functions
In mathematics, relationships between angles and side lengths play a crucial role in various calculations. The foundation of these relationships lies in functions that help describe these connections. These functions are essential for analyzing geometric shapes, solving problems, and modeling real-world phenomena. Understanding them is key to mastering more complex mathematical concepts.
Each function relates an angle to a ratio of two sides in a right triangle. These ratios are consistent and predictable, making them powerful tools for solving problems. The most common functions used in such calculations are:
- Sine: Relates the ratio of the opposite side to the hypotenuse of a right triangle.
- Cosine: Describes the ratio of the adjacent side to the hypotenuse.
- Tangent: Compares the opposite side to the adjacent side.
- Cosecant: The reciprocal of sine.
- Secant: The reciprocal of cosine.
- Cotangent: The reciprocal of tangent.
These functions allow us to calculate missing values in right triangles when given certain known values. As we delve deeper into their applications, we find they also extend into circular motion, waves, and other advanced mathematical fields.
Understanding how to manipulate these functions is essential for solving a wide variety of problems. To further reinforce the concepts, one can practice applying these ratios in different scenarios, from simple geometry to more complex calculations involving angles and circular motion.
How to Solve Trigonometry Problems
Succeeding in mathematical challenges involving angles and side lengths requires a clear approach to problem-solving. These problems often appear complex at first, but by breaking them down into smaller, manageable steps, anyone can find a solution. The key is knowing how to identify relevant information, apply the right formulas, and check your results for accuracy.
To begin, follow a structured method when approaching each problem. Here is a general approach to solving such exercises:
- Identify the given information: Understand what values are provided in the problem, such as side lengths or angles. This helps determine which formula or function to apply.
- Choose the correct function: Decide which of the basic ratios (sine, cosine, tangent, etc.) will help solve for the unknown value based on the given information.
- Set up the equation: Write the relevant ratio or formula and plug in the known values. Pay attention to the correct placement of the angle and the corresponding sides.
- Solve for the unknown: Perform the necessary arithmetic operations to isolate and find the value of the unknown quantity.
- Verify the solution: Double-check your calculations and the reasonableness of your result. Ensure the answer makes sense in the context of the problem.
By following these steps, you will be able to approach and solve most problems involving angles and side lengths. Practice is essential to develop speed and accuracy, but by mastering these steps, anyone can confidently tackle challenges of varying complexity.
Key Concepts in 8 4 Practice
Understanding the fundamental principles behind mathematical exercises involving angles and side ratios is essential for solving problems effectively. By mastering a few core concepts, anyone can gain the skills necessary to tackle more complex calculations. This section focuses on the key ideas that form the foundation for such problems.
Fundamental Principles
At the heart of solving angle-based problems are the relationships between the sides of right triangles. These relationships allow for the application of various functions to find unknown values. Some of the key concepts include:
- Ratios of sides: The basic ratios–sine, cosine, and tangent–are used to relate the angles of a triangle to the lengths of its sides.
- Angle relationships: Understanding how different angles interact within a triangle helps in identifying solutions.
- Reciprocal functions: The reciprocal functions such as cosecant, secant, and cotangent are essential when solving for unknown sides or angles.
- Unit circle: The unit circle provides a visual tool for understanding angle values and their corresponding side ratios, especially for non-right triangles.
Key Techniques for Solving Problems
Once these core concepts are understood, several techniques can be applied to solve a range of problems. A structured approach ensures that each part of the problem is addressed properly:
- Identifying known and unknown values: Begin by determining which values are provided and which need to be calculated.
- Choosing the correct function: Select the appropriate function (sine, cosine, tangent) based on the available information.
- Applying formulas: Use the selected function’s formula to set up an equation and solve for the unknown value.
- Checking results: After calculating, it’s crucial to verify the solution by rechecking the values and ensuring they fit the context of the problem.
Mastering these fundamental ideas and methods will help in navigating through more advanced topics and problems, allowing for a deeper understanding of geometric and angular relationships.
Step-by-Step Approach to Solutions
Solving mathematical challenges involving angles and side lengths becomes more manageable when approached methodically. A structured, step-by-step approach not only simplifies the process but also ensures that each part of the problem is addressed correctly. Following these clear steps helps in consistently reaching accurate solutions, even in complex situations.
Below is a detailed breakdown of the steps typically followed when working through such problems. This method will guide you from identifying known values to verifying your results for consistency.
| Step | Action | Details |
|---|---|---|
| 1 | Identify known and unknown values | Determine the given values in the problem and what needs to be calculated. |
| 2 | Choose the appropriate formula | Based on the problem’s context, select the correct function (e.g., sine, cosine, tangent) to relate the known and unknown values. |
| 3 | Set up the equation | Plug the known values into the formula and organize the equation to solve for the unknown value. |
| 4 | Solve for the unknown | Perform the necessary operations to isolate and find the value of the unknown quantity. |
| 5 | Check your solution | Recheck your calculations and confirm that the solution is logical in the context of the problem. |
By adhering to this methodical process, anyone can improve their accuracy and efficiency when solving such problems. With practice, this approach will become second nature, allowing for faster and more reliable results.
Trigonometric Ratios Explained
Understanding the fundamental ratios that relate the angles of a right triangle to the sides is key to solving many geometric problems. These ratios form the foundation for calculating unknown side lengths and angles in various scenarios. By mastering these basic relationships, one can easily approach and solve more complex exercises involving angles and distances.
Basic Ratios
There are six primary ratios used to describe the relationships between the sides of a right triangle. These ratios allow us to solve for missing sides or angles when other values are known. The most common ratios include:
- Sine: The ratio of the opposite side to the hypotenuse.
- Cosine: The ratio of the adjacent side to the hypotenuse.
- Tangent: The ratio of the opposite side to the adjacent side.
- Cosecant: The reciprocal of sine.
- Secant: The reciprocal of cosine.
- Cotangent: The reciprocal of tangent.
How to Use the Ratios
These ratios are used depending on the information available in the problem. For example, if the length of one side and an angle is known, the sine, cosine, or tangent ratio can be applied to find the missing side. Similarly, these ratios help in determining unknown angles by rearranging the formulas and using inverse functions.
By practicing and applying these ratios regularly, you can build a strong foundation in geometry and solve problems more effectively. Each ratio plays a vital role in different types of calculations, and understanding when to use each one is essential for successful problem-solving.
Common Mistakes in Trigonometry
Many students encounter challenges when solving problems that involve angles and side ratios. Even with a solid understanding of the concepts, it’s easy to make certain errors that can lead to incorrect solutions. Recognizing these common pitfalls can help improve accuracy and boost confidence when approaching these types of problems.
Common Errors in Calculations
One of the most frequent mistakes is misinterpreting which side of the triangle corresponds to which ratio. For instance, confusing the adjacent and opposite sides can lead to using the wrong function or applying it incorrectly. Additionally, neglecting to check the units of angles–whether in degrees or radians–can also cause significant errors in the final result.
- Incorrect function choice: Using sine instead of cosine (or vice versa) because of confusion about the sides.
- Forgetting to convert angles: When angles are given in radians instead of degrees, or vice versa, results can be inaccurate without proper conversion.
- Incorrectly using inverse functions: Using the inverse of a ratio when not needed can lead to finding the wrong angle or side.
Avoiding These Mistakes
The best way to avoid these common errors is through careful attention to detail and practice. Always ensure that you are working with the correct side lengths and functions, and double-check angle measurements. By recognizing these frequent mistakes and being mindful of them, you can significantly reduce errors and improve your problem-solving skills.
Using the Unit Circle in Problems
The unit circle is an invaluable tool for solving problems involving angles and their associated side ratios. It provides a geometric approach to understanding the relationships between angles and the coordinates of points on a circle, which simplifies many calculations. By referencing the unit circle, one can easily determine the sine, cosine, and other functions for various angles, both for standard and non-standard positions.
Understanding the Unit Circle
The unit circle is a circle with a radius of one, centered at the origin of a coordinate plane. The coordinates of any point on the circle correspond to the cosine and sine of the angle formed by the radius and the positive x-axis. This makes the unit circle an excellent visual aid for finding the values of these functions without needing complex calculations.
- Cosine: The x-coordinate of the point on the circle.
- Sine: The y-coordinate of the point on the circle.
- Tangent: The ratio of sine to cosine, or the slope of the line drawn from the origin to the point on the circle.
Applying the Unit Circle to Problems
When solving problems, especially those involving angles beyond 90 degrees, the unit circle can provide quick access to function values. For example, by identifying the corresponding point on the unit circle for a given angle, you can instantly know the values of sine and cosine for that angle. This technique is particularly useful for angles like 30°, 45°, and 60°, as their coordinates on the unit circle are well-known and easily remembered.
Additionally, for angles in different quadrants, the signs of the sine and cosine values change, which is another aspect the unit circle helps to clarify. By understanding these patterns, you can solve problems more efficiently and avoid common mistakes related to the signs of trigonometric functions.
Trigonometry Word Problems Simplified
Solving real-world problems that involve angles and distances can seem intimidating at first, but with a clear approach, they become much easier to manage. Word problems often present a scenario where the application of angle-based relationships between sides is necessary. Breaking down these problems step by step and identifying what is known and what needs to be solved will make the process more straightforward.
The key to simplifying word problems is to extract the relevant information, choose the right mathematical functions, and carefully set up equations. By following these steps, you’ll be able to approach each problem systematically and reach the correct solution. It’s also helpful to draw a diagram whenever possible, as this visual aid makes it easier to identify relationships between the elements of the problem.
One important thing to remember is that many word problems rely on the same principles and can be solved using basic concepts like ratios, angles, and known side lengths. Whether you’re working with a simple or more complex scenario, applying these fundamental rules can make word problems much less daunting and more manageable.
Tools to Aid Trigonometry Practice
There are several tools available that can significantly enhance the learning experience when working with angles, ratios, and side lengths. These resources can help clarify concepts, provide step-by-step solutions, and offer interactive ways to test knowledge. By integrating these tools into your study routine, you’ll gain a deeper understanding of the subject and become more proficient in solving problems.
Many students find that using visual aids, calculators, and specialized software makes it easier to understand and solve complex problems. These tools help reinforce the connections between angles, side ratios, and functions, which is crucial for mastering the material. Whether you’re practicing specific problems or preparing for exams, the right resources can provide invaluable assistance.
Helpful Tools
| Tool | Purpose |
|---|---|
| Graphing Calculators | Enable users to quickly compute values of sine, cosine, tangent, and other functions, as well as graph these functions for better visual understanding. |
| Interactive Websites | Provide dynamic practice problems, tutorials, and visual aids to better understand angle relationships and calculations. |
| Unit Circle Charts | Showcase the relationship between angles and their corresponding sine and cosine values, making it easier to recall important information. |
| Math Apps | Allow for step-by-step problem solving, providing immediate feedback on answers and helping users track their progress. |
By making use of these tools, you can quickly enhance your problem-solving skills and gain a stronger grasp of fundamental concepts. Whether you’re studying independently or as part of a group, these resources can make learning more effective and engaging.
Graphing Trigonometric Functions

Graphing functions that relate to angles is a powerful way to visually represent their behavior and understand their properties. By plotting these functions, you can observe how they vary with different angle measures and how they repeat over specific intervals. This visualization helps in identifying key characteristics such as amplitude, period, phase shifts, and symmetry, which are essential for solving many types of problems.
When graphing, it is important to understand the general shape and features of the function. Each function has its own unique pattern, and recognizing these patterns can make graphing much easier. The process involves choosing appropriate values for the angles and calculating the corresponding function values to plot points on the graph. By connecting these points, you create a curve that represents the function’s behavior over the specified range of angles.
Key Features of Graphs
- Amplitude: The vertical distance from the midline of the graph to the maximum or minimum value.
- Period: The horizontal length it takes for the graph to complete one full cycle.
- Phase Shift: A horizontal shift that moves the graph left or right along the x-axis.
- Symmetry: The graph often exhibits symmetry, with certain functions showing mirror-like patterns across specific axes.
Steps to Graph Trigonometric Functions
- Identify the function you are graphing (e.g., sine, cosine, tangent).
- Determine key characteristics such as amplitude, period, and any shifts.
- Choose values for the angle (typically in increments such as 0°, 30°, 45°, 60°, and 90°).
- Calculate the corresponding function values for each chosen angle.
- Plot these points on a coordinate plane.
- Connect the points to form a smooth curve, repeating the pattern as necessary.
By following these steps, you can successfully graph different functions, allowing you to visually interpret their behavior and make sense of the relationships between angles and side ratios. This is especially helpful for understanding periodic behavior in various contexts, from physics to engineering and beyond.
Review of Basic Trigonometric Identities
Understanding the fundamental relationships between angles and their corresponding functions is essential for solving a wide range of mathematical problems. These core principles, often referred to as identities, allow for the simplification of expressions and the solving of equations involving angles and ratios. Mastering these identities is key to developing a deeper understanding of more advanced concepts in mathematics and its applications.
At the heart of these relationships are a few key formulas that describe how the basic functions–such as sine, cosine, and tangent–interact with one another. By using these identities, you can manipulate and simplify expressions, helping to solve complex problems with ease. They are essential tools for simplifying calculations, transforming equations, and working through different types of mathematical challenges.
Below are some of the most commonly used identities that are crucial to your understanding:
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1
- Reciprocal Identities:
- sec(θ) = 1/cos(θ)
- csc(θ) = 1/sin(θ)
- cot(θ) = 1/tan(θ)
- Quotient Identities:
- tan(θ) = sin(θ) / cos(θ)
- cot(θ) = cos(θ) / sin(θ)
- Co-function Identities:
- sin(90° – θ) = cos(θ)
- cos(90° – θ) = sin(θ)
- tan(90° – θ) = cot(θ)
By becoming familiar with these identities and understanding how to apply them, you will gain the ability to simplify expressions, solve equations more efficiently, and deepen your grasp of mathematical concepts that rely on angle-based relationships.
Angles and Their Trigonometric Values
Angles are fundamental to understanding the relationships between various geometric shapes and their properties. Each angle can be represented using its sine, cosine, and tangent values, which provide essential information about the ratio of the sides of a right triangle. By calculating these values, we gain deeper insights into the properties of the triangle and the angles involved. These ratios are essential for solving numerous mathematical problems and are widely used in fields such as physics, engineering, and computer science.
For any given angle, the values of these functions help describe the position of points along the unit circle. By understanding how these functions change as the angle increases or decreases, we can predict their behavior and use this knowledge to solve problems that involve angles and sides.
Common Angles and Their Values
- 0°: sin(0°) = 0, cos(0°) = 1, tan(0°) = 0
- 30°: sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
- 45°: sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1
- 60°: sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3
- 90°: sin(90°) = 1, cos(90°) = 0, tan(90°) is undefined
Using Angles to Solve Problems
By knowing these standard angle values, it becomes much easier to solve problems that involve right triangles or circular motion. These key angles provide convenient reference points, simplifying calculations and helping to verify solutions. The ability to quickly recall these values speeds up the process of solving equations and drawing graphs of related functions.
Real-World Applications of Trigonometry
The study of angles and their relationships plays a significant role in a wide variety of fields beyond mathematics. By using the fundamental principles of angular measurements, professionals in many industries are able to solve practical problems and make informed decisions. From architecture to navigation, the knowledge of how angles and distances relate is essential for achieving accuracy and efficiency in various tasks.
One of the most common uses of these concepts is in construction, where precise measurements are needed to ensure the stability and alignment of structures. Similarly, engineers rely on these principles to design and analyze mechanical systems, electronics, and even software applications. Whether it’s for calculating the height of a building, determining the trajectory of a projectile, or optimizing the design of a component, these tools are crucial for problem-solving.
Key Industries Using Angle-Based Calculations
- Architecture: For designing structures, calculating roof angles, and ensuring correct alignment of various components.
- Aerospace Engineering: In calculating the trajectory of aircraft and spacecraft, as well as in designing flight paths and navigation systems.
- Geography and Cartography: Used to measure distances, map terrains, and create accurate representations of landmasses and environments.
- Physics: In studying waveforms, optics, and forces, where the behavior of angles significantly impacts outcomes.
- Computer Graphics: For rendering 3D models and simulations, where angles are essential to determine light reflections and object movements.
Practical Examples of Angle Calculations
- Surveying: Calculating land area and determining property boundaries using precise angle measurements.
- Navigation: Determining ship or aircraft positions by calculating course angles relative to known landmarks or celestial bodies.
- Medical Imaging: Using angular calculations to analyze data from MRI machines or CT scans to build accurate 3D models of body parts.
- Sound Engineering: In acoustics, to determine the reflection and absorption of sound waves based on their angles.
These examples highlight how abstract mathematical concepts are transformed into real-world solutions, proving that the understanding of angles and their properties is indispensable for tackling everyday challenges and advancing technology.
Trigonometry in Calculus and Beyond
The concepts of angles and their relationships continue to play a critical role as one moves into more advanced areas of mathematics. As students advance into fields like calculus, these foundational ideas become indispensable tools for solving complex problems. The study of functions involving angles extends far beyond basic geometry, influencing fields like physics, engineering, and computer science. The ability to model natural phenomena and solve real-world problems often relies on the understanding of angular relationships and their deeper implications.
In calculus, these principles help in differentiating and integrating functions that involve sinusoidal and other periodic behaviors. The powerful combination of limits, derivatives, and integrals provides the foundation for analyzing continuous changes in systems modeled by angle-based functions. For example, when solving oscillatory motion or wave behavior, trigonometric functions provide a means of expressing periodic changes, which are central to many areas of study.
Beyond calculus, the use of these principles expands into more specialized branches of mathematics and science. The study of differential equations, for instance, involves equations where rates of change are expressed through functions that rely on angle relationships. In physics, these same relationships are applied to describe wave patterns, sound, light, and even the behavior of particles at the quantum level.
Tips for Mastering Trigonometric Concepts
Understanding the relationships between angles and their mathematical representations is essential for excelling in this area of study. Gaining proficiency in these concepts requires both practice and a deep understanding of the foundational principles. Whether you are solving equations or analyzing geometric shapes, mastering these ideas will greatly enhance your problem-solving skills and open doors to more advanced topics. Here are some strategies that can help you succeed in mastering these fundamental concepts.
1. Focus on Core Functions and Relationships
The first step in mastering any subject is understanding its core functions. Spend time familiarizing yourself with the basic relationships that exist between angles and sides in different geometric figures. By grasping how these core functions work, you’ll have a solid foundation to build upon. Understanding sine, cosine, and tangent, for instance, is essential as these functions form the basis of many more complex formulas and problems.
2. Practice with Real-World Examples
Applying theoretical knowledge to real-world scenarios can help solidify your understanding. Try to solve problems that involve real-life situations, such as measuring distances using angles or analyzing motion in physics. The more you relate concepts to tangible examples, the easier it becomes to see how these ideas are used in various fields.
By combining these methods, you will develop a more comprehensive understanding of the concepts and be able to tackle problems with confidence. With dedication and the right approach, mastering these principles becomes a rewarding experience.
Practice Strategies for Trigonometry Success
Achieving success in mastering mathematical concepts involves more than just understanding the theory. Consistent application and effective problem-solving are key. To excel in this field, it’s important to develop strategies that enhance your skills and deepen your understanding. Below are some proven techniques to help you improve your abilities and perform confidently in problem-solving tasks.
1. Start with Simple Problems
Begin by solving basic problems to build a strong foundation. Focus on understanding the fundamental principles and step-by-step processes involved. Simple exercises can help you develop familiarity with the key concepts and lay the groundwork for tackling more complex challenges later.
2. Break Down Complex Problems
When confronted with a complicated problem, break it down into smaller, more manageable steps. This allows you to focus on one aspect of the problem at a time, reducing the likelihood of errors and making it easier to spot patterns and relationships. Analyzing problems in parts helps improve your logical thinking and approach.
3. Use Visual Aids
Visualizing concepts can significantly enhance your understanding. Drawing diagrams, using graphs, or applying geometric models can help you see the relationships between different elements. Whether it’s plotting functions or sketching triangles, these tools allow you to better grasp abstract ideas and reinforce your problem-solving skills.
4. Consistent Review and Reinforcement
Regularly revisiting concepts ensures that you retain the material and avoid forgetting key steps. Practice consistently over time rather than cramming. Reinforcement through repetition allows you to build fluency and familiarity with various techniques, making it easier to apply them when needed.
By following these strategies, you will strengthen your understanding, enhance your problem-solving efficiency, and approach tasks with greater confidence. Consistent effort and focused practice are essential for achieving mastery in this area.