
Preparing for an assessment in the field of electronics involves understanding fundamental principles that are crucial for developing efficient systems. A solid grasp of basic concepts and techniques is essential for tackling complex problems effectively. As you delve deeper into this area, you’ll find that each component plays an important role in the overall functionality of a system.
By focusing on core topics such as gate operations, simplification methods, and circuit behavior, you can enhance your ability to solve practical challenges. Success in this field not only requires theoretical knowledge but also the ability to apply it to real-world scenarios. Strengthening your understanding through practical examples will ensure you’re ready for any related task.
Practicing problem-solving regularly is the best way to reinforce your skills. This guide offers insights into common areas of focus and provides tips on how to approach typical challenges. Whether you are revising core ideas or tackling advanced scenarios, building confidence through consistent practice is key.
Key Topics in Circuit Analysis
Understanding the fundamental components and operations within electronic systems is essential for solving complex problems efficiently. There are several core areas that form the foundation of this field, each playing a crucial role in how systems are structured and function. Grasping these topics thoroughly will help in applying theoretical knowledge to real-world situations.
One of the primary areas to explore is how different gates perform basic operations and how they combine to create more complex functions. Equally important is the ability to simplify expressions and diagrams, which helps reduce complexity in practical applications. Another key area involves analyzing the timing and sequence of events within circuits to ensure they operate as intended.
Mastery of these areas also involves recognizing potential pitfalls and challenges, such as managing the flow of signals or handling synchronization. It is through understanding these essential concepts that one can successfully approach complex systems and design solutions with confidence.
Understanding Logic Gates and Their Functions
At the heart of every electronic system are basic building blocks that control how signals interact and influence the system’s overall behavior. These components, often referred to as gates, perform essential operations by taking inputs and generating specific outputs based on predefined rules. Their role is crucial in determining the functionality of more complex circuits, making them an indispensable part of system architecture.
Each gate performs a unique operation, such as combining or negating input signals to create desired results. Understanding the behavior of these gates allows one to construct and analyze various systems, from the simplest circuits to highly sophisticated systems.
| Gate | Symbol | Operation | Output |
|---|---|---|---|
| AND | ∧ | Outputs true only if all inputs are true | 1 if both inputs are 1, otherwise 0 |
| OR | ∨ | Outputs true if at least one input is true | 1 if at least one input is 1 |
| NOT | ¬ | Inverts the input | 1 becomes 0, 0 becomes 1 |
| XOR | ⊡ | Outputs true if exactly one input is true | 1 if inputs are different, otherwise 0 |
| NAND | ⊠ | Outputs true if not all inputs are true | 0 if both inputs are 1, otherwise 1 |
| NOR | ⊡ | Outputs true if neither input is true | 1 if both inputs are 0, otherwise 0 |
By mastering the functions of these gates, one can begin to build more complex systems, combining multiple gates to solve a variety of problems. Their versatility and simplicity make them the foundation of modern circuit design.
How to Solve Boolean Algebra Problems
When tackling problems in this area, the main objective is to simplify complex expressions into their most efficient form. By using a set of rules, one can manipulate these expressions to find solutions that are easier to work with in practical applications. Mastery of these techniques is essential for both analyzing and designing circuits that require optimal performance.
Key Simplification Techniques
The process involves applying certain properties and rules that help reduce the number of terms or operations needed. These principles include commutative, associative, distributive properties, along with others such as identity and complement laws. Each rule serves a specific purpose, allowing for a step-by-step simplification of the expression.
Common Boolean Identities
| Identity | Expression | Result |
|---|---|---|
| Identity Law | A + 0 = A | The result is the original variable. |
| Null Law | A * 0 = 0 | The result is zero. |
| Idempotent Law | A + A = A | The result is the same variable. |
| Complement Law | A * A’ = 0 | The result is zero. |
| Involution Law | (A’)’ = A | The result is the original variable. |
By recognizing these identities and applying them correctly, one can simplify even the most complex expressions with ease. Each step in the process brings the expression closer to its simplest form, helping to reduce the time and resources needed for implementation in real-world systems.
Designing Simple Combinational Circuits
Creating basic systems that perform specific tasks involves understanding how different components interact to produce a desired output based on the inputs. These systems can be built by combining simple elements that follow a set of rules, resulting in a reliable and predictable operation. The challenge lies in selecting the right components and connecting them effectively to achieve the goal.
Steps to Build a Simple Circuit
The first step is to determine the requirements of the system, including the number of inputs and the expected outputs. From there, you can identify the necessary components, such as gates or other elements, that will help you achieve the desired result. The next step involves drawing the system and planning the connections between the components to ensure correct operation.
Optimizing Circuit Performance
Once the basic structure is in place, the next task is to refine the design for efficiency. This can be done by minimizing the number of components used or by simplifying the connections between them. A well-designed system should not only function correctly but also be cost-effective and easy to implement.
Testing the system at various stages of the design process is essential to ensure its functionality. By running different scenarios, you can verify that the outputs are consistent with the expected results. Troubleshooting any issues early in the process will help avoid complications down the line.
Building simple systems can seem straightforward, but it requires careful planning and attention to detail. Once the fundamentals are mastered, more complex systems can be tackled with greater confidence.
Analyzing Truth Tables for Circuit Design
Understanding how different inputs affect the behavior of a system is essential for constructing reliable and predictable systems. One of the most effective ways to map out these relationships is by using tables that represent all possible input combinations and their corresponding outputs. These tables provide a clear, structured method for analyzing and verifying the functionality of a circuit.
How to Create a Truth Table
To begin, you need to list all possible input combinations for the system. The number of combinations depends on the number of variables involved–each additional input doubles the number of rows in the table. Once the inputs are laid out, you can determine the output for each combination based on the rules of the system or the specific components used.
- Start by identifying the number of inputs in the system.
- List all possible combinations of input values (0 or 1).
- Determine the output for each input combination based on the circuit’s behavior.
- Fill in the table with the results of each combination.
Interpreting the Results
Once the table is complete, you can use it to gain valuable insights into how the system behaves. For example, you can identify patterns in the outputs that suggest optimization opportunities or potential issues. Additionally, comparing the truth table with the desired behavior allows you to ensure that the system operates as expected in all scenarios.
- Check if the system behaves as intended for all combinations.
- Look for cases where the output may not match the expected result.
- Use the table to guide adjustments in the system or to simplify the design.
Truth tables are invaluable tools for verifying the correctness of a system’s functionality and making informed decisions during the development process. By carefully analyzing the table, you can ensure the circuit meets all requirements and functions smoothly under various conditions.
Mastering Karnaugh Maps for Simplification
When dealing with complex expressions, one of the most effective methods for simplifying and optimizing systems is by using a visual approach. Karnaugh maps provide a way to organize and analyze data, making it easier to spot patterns and reduce expressions systematically. This method helps streamline the design process, leading to more efficient and less error-prone solutions.
How Karnaugh Maps Work
Karnaugh maps are essentially grids that represent all possible combinations of variables in a system. By placing the values of a Boolean expression into these grids, you can visually group adjacent cells that contain the same value. This makes it easier to simplify the expression by applying Boolean rules such as combining terms and eliminating redundancies.
- Start by creating a grid based on the number of variables involved.
- Label each cell in the grid with the appropriate value from the Boolean expression.
- Look for adjacent cells that contain identical values and group them together.
- Apply Boolean simplification rules to combine these groups and eliminate unnecessary terms.
Optimizing the Expression
Once you’ve grouped adjacent cells, you can apply simplification techniques to reduce the overall expression. The goal is to create a more efficient system by removing redundant components, which reduces the complexity of the circuit or system being designed. This can lead to less power consumption, faster processing, and lower costs.
- Identify the largest possible groups that can be combined.
- Simplify the expression by eliminating redundant variables in each group.
- Check the final expression to ensure it accurately represents the original system’s behavior.
By mastering Karnaugh maps, you can significantly improve your ability to design optimized systems. This method is especially useful when dealing with larger expressions, where traditional algebraic simplification would be too time-consuming or complicated.
Sequential Logic vs Combinational Logic
Understanding the distinction between two fundamental types of systems is crucial for anyone involved in creating complex circuits. One category operates purely based on current input values, while the other takes past inputs into account, allowing for more dynamic behavior. Both approaches have their own strengths and applications, depending on the task at hand.
Combinational Systems
Combinational systems are defined by their immediate output, which is determined solely by the current input. These systems do not rely on previous states, making them simpler in design and operation. They are widely used in applications where the output is directly related to the input at any given time.
- Output depends entirely on the current input values.
- No memory or past input is needed.
- Examples include arithmetic operations, multiplexers, and encoders.
Sequential Systems
Sequential systems, on the other hand, include memory elements that store previous inputs, meaning their output depends not just on current inputs but also on prior states. These systems are crucial for applications that require timing, memory, or the ability to change behavior based on a sequence of events.
- Output depends on both current and past input values.
- Incorporates memory elements such as flip-flops and registers.
- Examples include counters, shift registers, and state machines.
Key Differences
- Combinational systems are simpler and faster, as they require no memory.
- Sequential systems are more complex but allow for greater functionality, such as storing states or managing sequences.
- Combinational systems provide immediate responses, while sequential systems take time to change states based on inputs.
Both types of systems are essential in modern circuit design, often working together to achieve the desired functionality. The choice between the two depends on the specific requirements of the system being developed.
Flip-Flops and Their Applications
Memory elements play a crucial role in modern systems by allowing for the storage of information over time. Flip-flops are one of the most fundamental components used for this purpose. These devices are capable of holding a binary state, enabling circuits to remember data and retain it until needed. Their ability to maintain a state until explicitly changed makes them essential in many applications, particularly in sequential systems.
Understanding Flip-Flops
Flip-flops are bistable devices, meaning they have two stable states. Each state represents a different value, typically 0 or 1. The flip-flop changes its state based on input signals and control mechanisms, providing a way to store bits of data. They are often used in situations where it’s necessary to store or synchronize information across a system.
- Two stable states: high (1) or low (0).
- State changes occur based on clock signals or other input triggers.
- Common types include D, T, SR, and JK flip-flops.
Applications of Flip-Flops
Flip-flops are widely used in systems that require memory, timing, or synchronization. Their versatility allows them to be used in a variety of applications, from simple data storage to more complex tasks like synchronization and sequencing.
- Data Storage: Flip-flops are used in registers to store individual bits of data.
- Clock Dividers: They can divide clock frequencies in timing circuits.
- State Machines: Flip-flops are essential for building sequential logic circuits, such as finite state machines.
- Counters: They are integral parts of counters, which track the number of clock pulses or events.
- Designing sequential circuits often involves multiple flip-flops working together to store and process information.
- In memory devices, flip-flops help store single-bit data, enabling data retention during power cycles.
- In control systems, flip-flops help synchronize operations across different parts of the system, ensuring reliable and orderly operation.
In summary, flip-flops are indispensable building blocks in many systems where memory and state retention are required. Their ability to maintain stable states while responding to control signals makes them essential in both simple and complex circuits alike.
Designing Counters for Digital Circuits
Counters are fundamental components in many systems, where their primary function is to keep track of events or time intervals. These devices increment or decrement in response to clock signals, making them essential for various applications such as frequency division, event counting, and timing. By accurately tracking the number of occurrences, counters are key elements in creating more complex sequential circuits and systems.
Types of Counters
Counters can be classified into several categories, each serving different purposes based on their counting method and behavior. The most common types are the up-counter, down-counter, and the up/down-counter. Understanding the characteristics of each type allows for better selection depending on the needs of the application.
- Up-Counter: Counts upward from a specified starting value, typically starting at zero and incrementing with each clock pulse.
- Down-Counter: Counts downward from a preset maximum value, decreasing with each clock pulse.
- Up/Down Counter: Allows for both upward and downward counting based on the direction control input.
Design Considerations
When designing counters, there are several key aspects to consider in order to ensure proper functionality and efficiency. These include the clock source, the counting direction, and whether the counter should reset after reaching a certain limit. Counters are often designed using flip-flops and other sequential elements, allowing for the desired behavior and ensuring that the system operates as expected.
- Clock Input: The clock signal drives the counting operation, determining how often the counter increments or decrements.
- Reset Mechanism: Many counters feature a reset function that allows them to start counting from a known value, typically zero, after reaching a maximum or minimum count.
- Modular Design: Counters are often modular, meaning multiple stages of counting can be chained together to create larger counters with different range capabilities.
Incorporating counters into a system adds significant functionality, particularly when working with timing, event tracking, or frequency division. Their versatility and simplicity make them indispensable tools in circuit design, whether in digital clocks, timers, or other sequential systems.
Common Digital Logic Design Errors
When creating complex circuits, even small mistakes can lead to significant malfunctions. Understanding the most common errors helps avoid costly troubleshooting and ensures that the system performs as intended. Mistakes can range from simple oversights in component connections to more complex issues in timing and logic state management. Being aware of these pitfalls is crucial for anyone involved in creating sequential or combinational systems.
Wiring Mistakes
Incorrectly connecting components is one of the most frequent causes of circuit failures. These mistakes can occur during the design phase or physical construction of the system. Common errors include incorrect pin assignments, missed connections, or improper routing of signals.
- Misplaced Wires: Incorrectly connecting components can cause unexpected behaviors, such as short circuits or failure to trigger specific outputs.
- Unconnected Pins: Failing to properly connect input or output pins often results in a system that doesn’t function or produces erroneous results.
- Incorrect Voltage Levels: Applying incorrect voltage to certain components can damage them or prevent the circuit from operating properly.
Timing Issues
Another critical area where errors often arise is timing. Timing issues occur when signals are not synchronized properly, leading to incorrect behavior or failure of the circuit to reach the desired state at the right time.
- Clock Skew: When the clock signal reaches different parts of the system at different times, it can cause inconsistent behavior, especially in sequential systems.
- Improper Set-Up or Hold Times: Data inputs may change before the system is ready to register them, leading to race conditions or unreliable outputs.
- Reset Timing: Failing to properly implement reset sequences can cause the circuit to behave unpredictably or fail to start correctly.
Faulty Component Selection
Choosing the wrong components or failing to meet the required specifications can cause the system to malfunction. For example, selecting components with incompatible voltage levels, insufficient speed, or inadequate power ratings can result in suboptimal performance.
- Inadequate Power Rating: Components that cannot handle the required power may overheat, burn out, or cause failures within the system.
- Incompatible Components: Using components that do not meet the necessary operational standards or specifications leads to incompatibility issues and can render the system inoperable.
Design Oversights
Omissions or poor planning in the initial stages of system design can lead to a variety of issues. Overlooking important details such as signal integrity, feedback loops, or edge cases can compromise the functionality of the system.
- Lack of Signal Filtering: Without proper filtering or noise suppression, signals may become distorted, leading to errors or unreliable performance.
- Unaccounted Feedback Loops: Not considering feedback mechanisms in the system can cause oscillations or unstable states.
By recognizing and addressing these common errors early in the process, designers can create more reliable, efficient systems that perform as expected. Preventing mistakes at the design and implementation stages saves time, reduces costs, and results in more robust, functional circuits.
Using Multiplexers in Logic Design
Multiplexers are versatile components widely used to manage the flow of data within systems. They allow multiple input signals to be directed to a single output, based on a selection signal. This ability to control which data is passed through makes them essential for various applications, including data routing, signal switching, and reducing the complexity of circuit design. Their use streamlines the operation of circuits, providing an efficient way to handle multiple inputs with fewer components.
Functionality and Operation

A multiplexer, often abbreviated as MUX, is typically described by the number of input lines it can manage. The most common multiplexers include 2-to-1, 4-to-1, and 8-to-1 configurations, where the number indicates the number of data inputs. The multiplexer has a set of select lines, which determine which input is routed to the output. The select lines act as a control mechanism, switching between inputs based on the desired configuration.
- 2-to-1 Multiplexer: It selects one of two data inputs based on a single select line, sending the chosen input to the output.
- 4-to-1 Multiplexer: This version has four data inputs and two select lines, which can choose any one of the four inputs to pass through to the output.
- 8-to-1 Multiplexer: A more complex version, with eight inputs and three select lines, allowing for even more control over which input is connected to the output.
Applications of Multiplexers

Multiplexers are widely used in systems where data needs to be transmitted efficiently, especially in digital circuits where multiple data streams must be handled simultaneously. One of the key advantages is their ability to reduce the number of wires needed in a system, as a single multiplexer can replace several parallel data paths.
- Data Routing: In communication systems, multiplexers are used to route data from one source to various destinations, minimizing the need for redundant connections.
- Signal Switching: Multiplexers serve as signal selectors, allowing circuits to switch between different input signals depending on the control logic.
- Function Minimization: By using multiplexers, complex logical operations can be simplified, enabling more efficient use of available hardware resources.
Incorporating multiplexers into a system helps optimize performance, reduce the complexity of the circuit, and improve overall efficiency. Their flexibility and ease of use make them an invaluable tool in modern electronic design.
Understanding State Diagrams in Digital Systems
State diagrams are visual representations that map out the behavior of systems over time, highlighting how they transition between different conditions based on inputs and previous states. These diagrams are vital tools in understanding the sequence of operations in sequential circuits and help to clarify the flow of data and control within a system. By breaking down complex processes into states, these diagrams make it easier to analyze, design, and troubleshoot digital systems.
Key Elements of State Diagrams
State diagrams consist of several key components that define how a system operates. These elements include:
- States: Each state represents a specific condition or mode of the system, where certain actions or outputs are determined.
- Transitions: These are the arrows connecting different states, indicating how the system moves from one state to another based on specific conditions or inputs.
- Events or Inputs: The conditions that trigger transitions from one state to another, such as changes in input values or external signals.
- Outputs: The results or actions that occur when the system is in a particular state or when a transition is made.
How State Diagrams Simplify System Analysis
State diagrams provide a clear and structured way to visualize the flow of a system, making it easier to understand the system’s behavior under different conditions. By following the state transitions, designers can predict the system’s response to various inputs and ensure that it operates correctly across all possible scenarios.
- Identifying State Sequences: State diagrams allow for easy identification of the sequence in which a system changes states, ensuring that no step is missed and helping in the detection of potential issues.
- Minimizing Complexity: Complex systems can be broken down into simpler sub-processes, each represented as a state, which reduces the overall complexity of analysis and design.
- Improved Troubleshooting: When issues arise in a system, state diagrams help pinpoint exactly where a malfunction might occur by examining the states and transitions that led to the error.
State diagrams are essential tools for anyone working with systems that rely on sequential processes. They provide clarity, structure, and efficiency, making them indispensable in the analysis and design of functional systems.
Minimizing Logic Circuits with Quine-McCluskey

The Quine-McCluskey algorithm is a methodical approach used to simplify complex circuits by minimizing the number of logic gates needed to perform a specific function. This process helps in reducing the overall complexity, cost, and power consumption of a system. By transforming a Boolean expression into a more efficient form, designers can improve the performance and reliability of a circuit. The technique involves finding essential prime implicants and eliminating redundant terms from the original expression.
Step-by-Step Process of Quine-McCluskey
To use the Quine-McCluskey algorithm, the initial Boolean expression is first represented in a tabular form, listing all the minterms. Then, pairs of terms that differ by only one bit are combined, gradually simplifying the expression. The process is repeated iteratively, reducing the number of terms until the simplest possible form is achieved.
- Step 1: List all the minterms of the Boolean function in a table.
- Step 2: Compare pairs of minterms and group those that differ by only one variable.
- Step 3: Repeat the grouping process, continually combining terms that share common elements.
- Step 4: Extract the prime implicants, eliminating any redundancies.
- Step 5: Finalize the simplified Boolean expression.
Benefits of Using Quine-McCluskey
By applying this method, designers can achieve significant reductions in the number of gates required for circuit implementation. This not only lowers the material cost but also improves the efficiency of the circuit. Additionally, simplifying Boolean functions reduces the likelihood of errors in logic, resulting in more reliable and stable systems.
- Efficiency: Reduces the number of gates needed, optimizing both space and power consumption.
- Simplicity: Transforms complex Boolean functions into simpler, easier-to-implement forms.
- Automation: Can be implemented in software tools, speeding up the design process.
Quine-McCluskey is an essential tool for engineers and designers, offering a powerful means of simplifying circuit designs and ensuring optimal performance.
Solving Complex Timing Problems in Circuits
Timing issues are a critical aspect of circuit design, as they can lead to errors in the operation of a system. These issues arise when signals are not synchronized properly, causing delays or misfires in circuit responses. Properly managing the timing of signals is essential to ensuring that the system functions as intended. This section explores strategies for identifying and solving complex timing problems to improve the reliability of circuits.
One of the most common causes of timing problems is race conditions, where multiple signals influence the output of a circuit simultaneously. These conditions can cause unpredictable results. By ensuring that the signals are correctly timed and sequenced, designers can minimize the risk of such issues. Additionally, understanding propagation delays, setup times, and hold times is key to solving timing-related problems.
Key Concepts in Timing Analysis
To address timing issues, a designer must understand the core concepts that contribute to proper synchronization. These include propagation delay, which refers to the time it takes for a signal to travel through a gate, and setup and hold times, which define the minimum intervals for stable data input and output.
| Term | Definition |
|---|---|
| Propagation Delay | The time it takes for a signal to pass through a logic gate. |
| Setup Time | The minimum time before the clock edge when data input must be stable. |
| Hold Time | The minimum time after the clock edge during which data must remain stable. |
Approaches to Solving Timing Issues
One approach to solving complex timing problems is to use timing diagrams, which visually represent the relationship between clock signals and the data flow in a circuit. These diagrams help to identify when data is properly aligned with clock pulses and when delays or violations occur.
- Clock Skew: Ensuring that the timing of the clock signal is consistent across the circuit is crucial to preventing errors.
- Buffering: Adding buffers can help manage signal delays and ensure proper synchronization between components.
- Optimizing Setup and Hold Times: Fine-tuning the setup and hold times ensures that data is stable when read or written.
- Redesigning Critical Paths: Identifying and modifying critical paths that experience excessive delays can help meet timing requirements.
By carefully analyzing these aspects and implementing solutions like proper signal routing, use of buffers, and adjusting timing margins, designers can overcome timing challenges and ensure their circuits perform efficiently and reliably.
Tips for Acing Digital Logic Design Exams
Preparing for assessments in circuit theory and related subjects can be a daunting task, especially when complex concepts and intricate systems are involved. However, with the right approach, students can master the material and improve their performance significantly. This section highlights effective strategies to help you prepare for these types of assessments, ensuring that you feel confident and ready on the day of the test.
Master the Basics: A solid understanding of the fundamental principles is key to excelling. Be sure to familiarize yourself with core concepts such as binary arithmetic, truth tables, Boolean algebra, and timing diagrams. These foundational elements are often the building blocks for more complex problems, so having them well understood will make tackling advanced questions easier.
Practice with Past Problems: One of the best ways to prepare is by practicing past problems and exercises. This not only helps you get familiar with the types of tasks that may appear on the assessment but also allows you to refine your problem-solving techniques. Work through sample circuits, simplify Boolean expressions, and analyze different configurations to increase your speed and accuracy.
Effective Study Habits
Organize Your Study Sessions: Break your study sessions into focused intervals, giving each topic enough time for review. Avoid cramming the night before; instead, spread your study sessions out over several weeks, revisiting the material periodically. This will improve retention and comprehension.
Utilize Visual Aids: Visual aids, such as diagrams, charts, and flowcharts, can help you better grasp abstract concepts. For example, drawing out state diagrams, timing charts, or Karnaugh maps can help you visualize how signals propagate through systems. The more you practice drawing and interpreting these visual tools, the easier it will be to solve related problems during the test.
Test-Taking Strategies
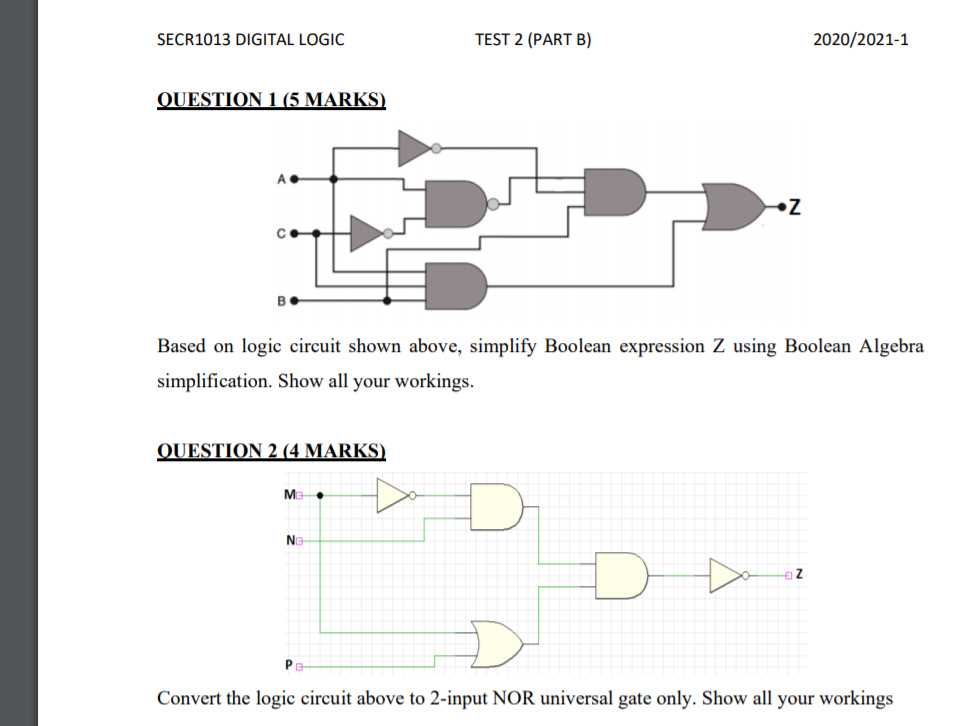
Read Questions Carefully: During the assessment, take time to read each question thoroughly before attempting to solve it. Many students lose valuable points simply because they misread the instructions or overlook key details. Pay close attention to any constraints or special instructions given in the problem.
- Start with What You Know: Begin by solving the problems you feel most confident about. This will help build momentum and reduce any anxiety.
- Show Your Work: Writing out each step of your solution not only helps ensure accuracy but also allows partial credit for correct reasoning, even if you make minor mistakes along the way.
- Time Management: Allocate time to each problem based on its complexity. If you get stuck on a question, move on and come back to it later.
Review Your Work: If time permits, go back over your answers to ensure you didn’t miss any important details. A quick review can often help you spot mistakes and make the necessary corrections before submitting your test.
By following these tips and staying consistent in your preparation, you’ll increase your chances of performing well and mastering the subject. Confidence, practice, and attention to detail are the keys to success in this area.